弯扭耦合风力机叶片的准稳态响应及LLTR控制
2018-08-01刘廷瑞
刘廷瑞, 常 林
(山东科技大学 机械电子工程学院过控系,青岛 266590)
风力机叶片的颤振分为线性经典颤振和失速非线性颤振两大类,这两大类颤振经常表现在叶片的挥舞方向和扭转方向耦合(弯扭耦合)的振动过程中,其中挥舞方向的失速颤振造成的发散不稳定是叶片断裂失效的重要原因之一[1]。而近年来在极端风速状态下,经常能检测到另外一种处于经典颤振和失速颤振临界状态的临界颤振[2],该颤振发生时叶片处于一种准稳态响应状态。其中挥舞方向的临界颤振引起的发散不稳定,不仅能造成叶片的断裂失效,还经常能造成塔体拦腰折断现象。鉴于此,本文针对挥舞/扭转耦合风力机叶片的发散不稳定问题,阐述弯扭耦合叶片的准稳态响应及临界颤振的LLTR控制过程。
风力机叶片的准稳态响应鲜有论及,现有文献主要针对停机状态下的静态风振及前述其它两种颤振状态进行研究。柯世堂等[3]基于大涡模拟方法研究了停机状态下不同叶片位置对MW级风力机塔架-叶片体系风振响应的影响。Baran等[4]通过BLADEMODE和PHATAS两种软件,基于Theodorsen技术研究了风力机2D叶型截面的经典颤振及其复杂的理论应用背景信息。刘廷瑞详细研究了风力机复合材料薄壁叶片在无阻尼和阻尼两种情况下的经典颤振和失速颤振问题。Laxman等[5]虽然同时研究了准稳态响应和失速响应问题,但却局限于前向飞行的直升机叶片。
线性二次型(Linear Quadratic,LQ)控制通常用来控制复合材料薄壁旋转梁的振动行为。Shete等[6]利用线性二次型调节器(Linear Quadratic Regulator,LQR)实现了基于周向统一刚度铺层薄壁旋转梁的频率调节和自由振动幅度控制,但未涉及气弹行为;Song等[7]利用线性二次型高斯(Linear Quadratic Gaussian, LQG)控制器实现了超音速复合材料层合圆柱壳的气热弹性特性分析及振动控制。Labane等[8]基于最优Kalman滤波设计,分别利用LQR、LQG两种控制器进行了飞行器气弹系统的控制;Rene等[9]则基于遗传算法,最优化了LQG控制器的性能。但在发散系统的控制中,LQR控制器即使在合理选择Q、R矩阵的情况下,其被控对象的初始响应经常具有较大的幅度;而LQG控制器本身的响应幅度也经常较大,且其滤波器的动态特性也经常大大快于反馈系统本身的特性[10-11]。
本文在前人工作的基础上[12],提取并修正了一种适合于风力机叶片的准稳态气动力,研究基于周向反对称刚度铺层的复合材料薄壁单闭室S809Ⅱ型翼型[13]叶片的临界颤振状态及颤振抑制方法。同时为解决上述LQG控制器的不足,在LQG控制策略中引入回路传输恢复,形成新的LLTR控制器,可以使LQG结构下的开环传递函数尽可能接近直接反馈时的频域响应。
1 准稳态气动力及气弹系统
S809Ⅱ型翼型叶片的复合材料基体铺层采用周向反对称刚度铺层,薄壁单闭室复合材料截面的位移和气动力分布,如图1所示。z方向代表挥舞方向,x为展长方向,θ为展长方向的弹性扭转;α为攻角;U为风速;c为弦长;叶片长度L;V0为相对风速;F为准稳态气动升力;M为准稳态气动力矩。叶片结构参数如表1所示。
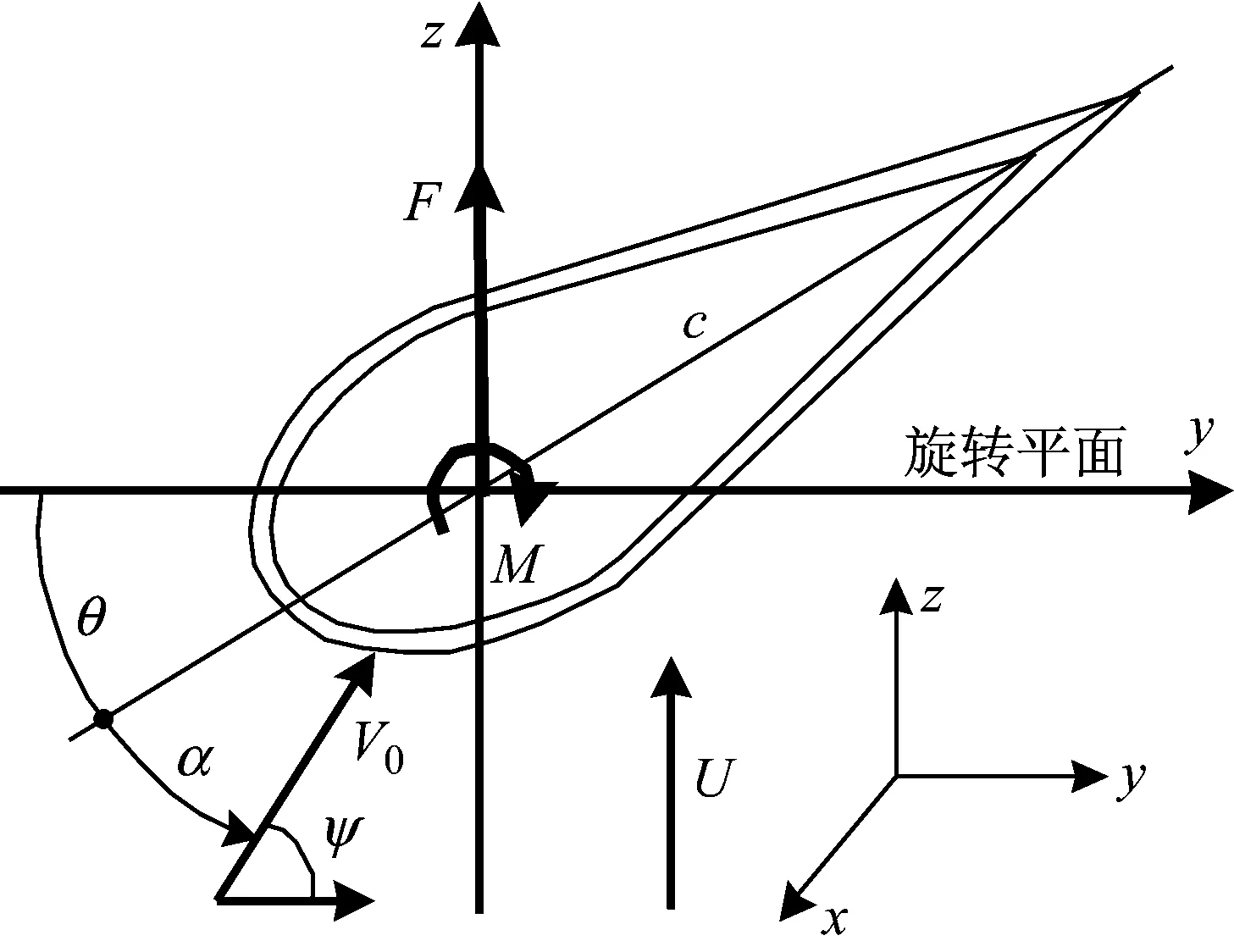
图1 翼型位移及准稳态气动力
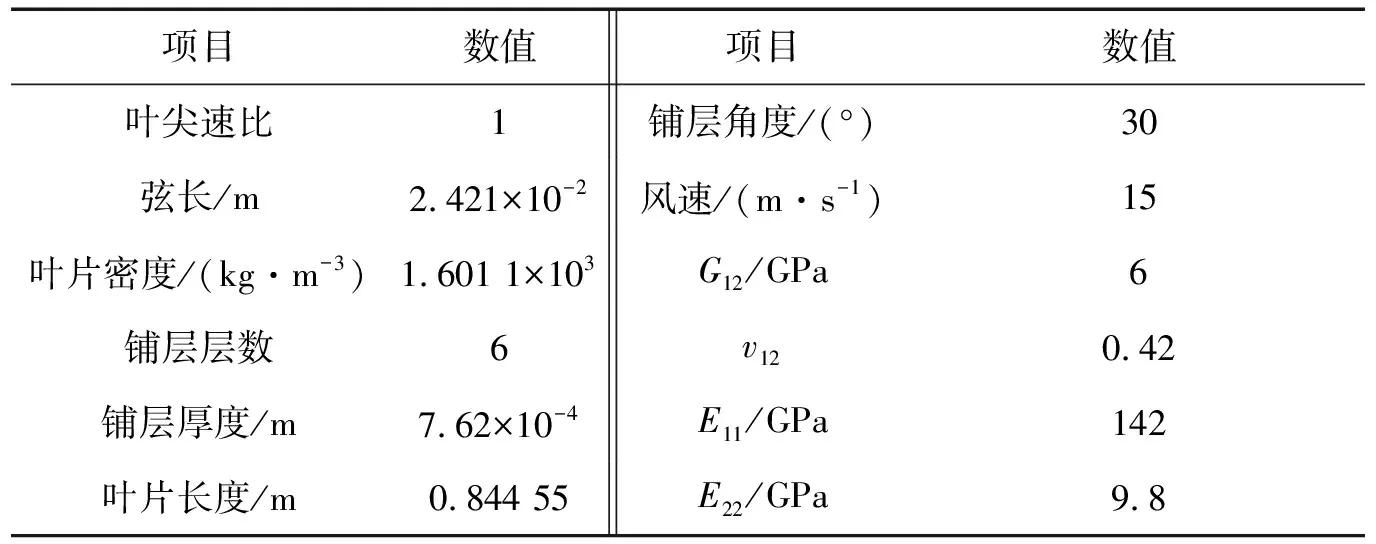
表1 叶片参数
准稳态气动力临界状态响应研究始于直升机叶片,其表达式来源于前向飞行直升机叶片的失速非线性气动力模型。不同学者推导了不同的失速气动力模型,Greenberg推导了直升机叶片的Greenberg失速不稳定气动力模型,该模型包含有升力缺损函数C(K),该函数与Baran的Theodorsen经典气动力缺损函数具有类似的形式,故可以提取其线性部分作为准稳态气动力模型。Laxman等在Greenberg的基础上,令C(K)≡1,而得到直升机叶片的准稳态气动力表达式。鉴于该表达式适合于处理前向飞行运动,故需将表达式中的谐波风速和变桨角分别替换为风力机叶片的相对风速V0和攻角α,才能近似描述风力机叶片的运动。替换后的表达式包括升力和力矩两部分,分别为
(1a)
(1b)
式中:ρa为空气密度,Ae为翼型截面面积,b为半弦长;气动变量W0、W1分别为
考虑周向反对称刚度铺层设计,且在不计阻尼效应的基础上,对称薄壁结构可以完全退化为弯扭耦合数学模型,同时结合动力刚化效应,转速为Ω的旋转叶片的扭转、挥舞运动方程可以分别描述为

(2a)
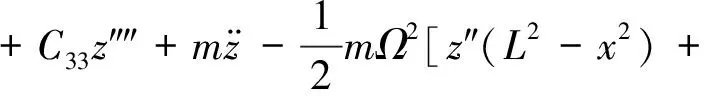
z′(-2x)]=F
(2b)
式中:m为单位长度质量;I是单位长度极惯性矩;C33,C22,C23分别是截面弯曲刚度、扭转刚度,以及弯扭耦合刚度,表达式详见文献[1]。其它系数参数分别为
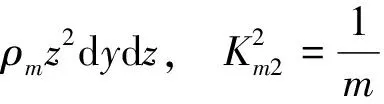
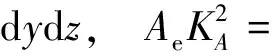
将式(1)代入式(2)得到气弹方程组,利用Galerkin法沿展长积分,进行离散化处理,可以得到线性二阶气弹方程组
(3)
式中:X是由2N个结构变量组成的离散化坐标变量(此处N=5为Galerkin法振型函数个数);MM、CM、KM分别为气弹系统的质量、阻尼和刚度矩阵。
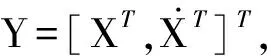
(4)
其中,Yout为一阶模型的输出,C为4N×4N单位矩阵。
2 LLTR控制
本文LLTR控制是在LQG控制策略的基础上,引入回路传输恢复方案实现LQ控制,进一步在准稳态响应分析的基础上实现颤振抑制。准稳态气动力作用下的叶片处于临界运行状态,在风速作用下,极易引入干扰信号和高频噪声,通常以白噪声的形式附加于式(4)中,而LLTR控制器可以对该类干扰和噪声起到抑制作用。本文通过两种不同的LLTR控制方案来分析控制性能,并通过半实物仿真实验平台来验证LLTR控制算法的实时效应。
首先采用一种分离原理来构建LQG控制结构:在控制过程中,单独处理最优估计问题与最优控制问题,并合并这两个问题的解从而得出最优解,如图2所示。
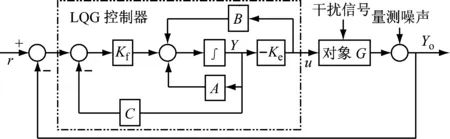
图2 LQG控制过程
其次,由于临界状态的干扰信号和高频噪声的作用,当LQG控制器的稳定裕度较小的时,极容易使系统变得不稳定。而在LQG基础上引入回路传输恢复技术实现LLTR控制,则可有效解决这一问题[14-15],具体过程如下:
(1) 确定Q、R值。首先设计最优LQR调节器,并调整Q、R值,使开环传递函数-Kc(SI-A)-1B的性能达到满意效果(Kc为期望的状态反馈矩阵)。其次令Q=CTC,并改变R的值使系统的开环传递函数接近直接反馈传递函数。
(2) 确定虚拟噪声系数q。选定q,使得观察器的Riccati方程满足
ΓΘΓT=0
(5)
其中,W、V由LQG控制器确定,Г取决于对象噪声的协方差矩阵,Θ为量测噪声的协方差矩阵。Pf为对称半正定矩阵,由Kalman滤波器向量Kf所决定。
(3) 两种LLTR控制器。文献大多基于系统输入端回路恢复进行控制。出于比较目的,本文同时采用了另一种输出端回路传输恢复设计。输入端回路传输恢复、输出端回路传输恢复分别满足
KC(sI-A)-1B
(6a)
C(sI-A)-1Kf
(6b)
其中,实际的虚拟噪声系数q取值是由不同的噪声系数组成的、顺次递增的包含4N+1个元素的行向量。
本设计虚拟噪声系数取行向量q=[1 1×1011.1×1011.2×1011.3×1011.4×1011.5×1011.6×1011.7×1011.8×1011.9×1011.1×1021.2×1021.3×1021.4×1021.5×1021.6×1021.7×1021.8×1021.9×1022×102]。此处最大幅度取为102,原因见后述实验部分。
3 仿真与讨论
为充分模拟极端风速下的发散状态,叶片结构未计算阻尼效应(阻尼效应的计算可参考文献[1]所示),以使叶片在风速U=15 m/s时,便出现极端发散状态。图3(a)和(b)分别展示了U=15 m/s时,叶尖扭转和挥舞弯曲均处在极端发散状态。扭转位移在2 s内便达到70 rad,而挥舞位移则达到1 m(超过了叶片本身的长度)。随着时间的推移,发散数值会不断持续加大,此为数字仿真结果,如果出现在实践当中,则会引起叶片甚至塔体的破坏性断裂失效。
图3(c)为LQG控制下的扭转/挥舞位移响应,虽然直观上看来,两个原本发散的运动在极短时间内快速收敛,体现了很好的收敛稳定性。而实际上扭转位移收敛于12.5 rad,相对于叶片长度L仍然显得过大,且挥舞位移稳定在6.2 m也是不现实的,远远超过了叶片的实际长度L,故从工程实际的角度考察,图3(c)仍然是处于发散不稳定的状态。图3(d)展示了LQG控制器响应的幅度,对每一个变量的控制量都是常值,可以看出第6~10个变量(恰好对应于挥舞位移)的控制响应幅度波动不稳定,甚至达到了106的数量级,这是用过大的能量去控制发散的理论仿真结果,是不现实的,在实际控制中往往会出现精度和可靠性问题,比如控制器处理的溢出问题、对硬件的瞬时冲击破坏问题等等。这也正是本文应用LLTR控制进行折中处理的原因。
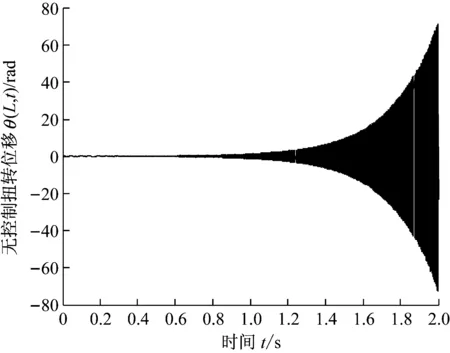
(a) 无控制扭转位移
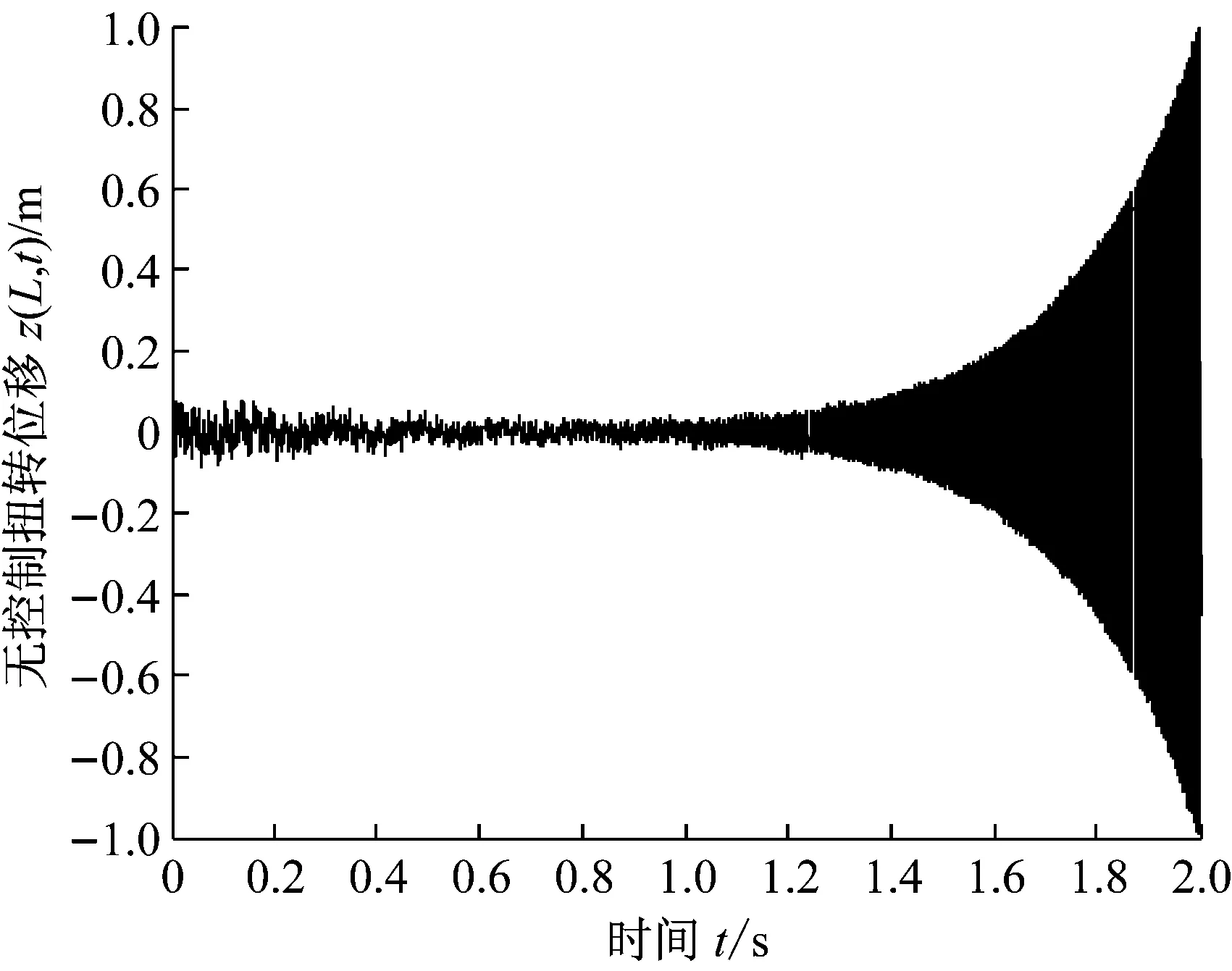
(b) 无控制挥舞位移
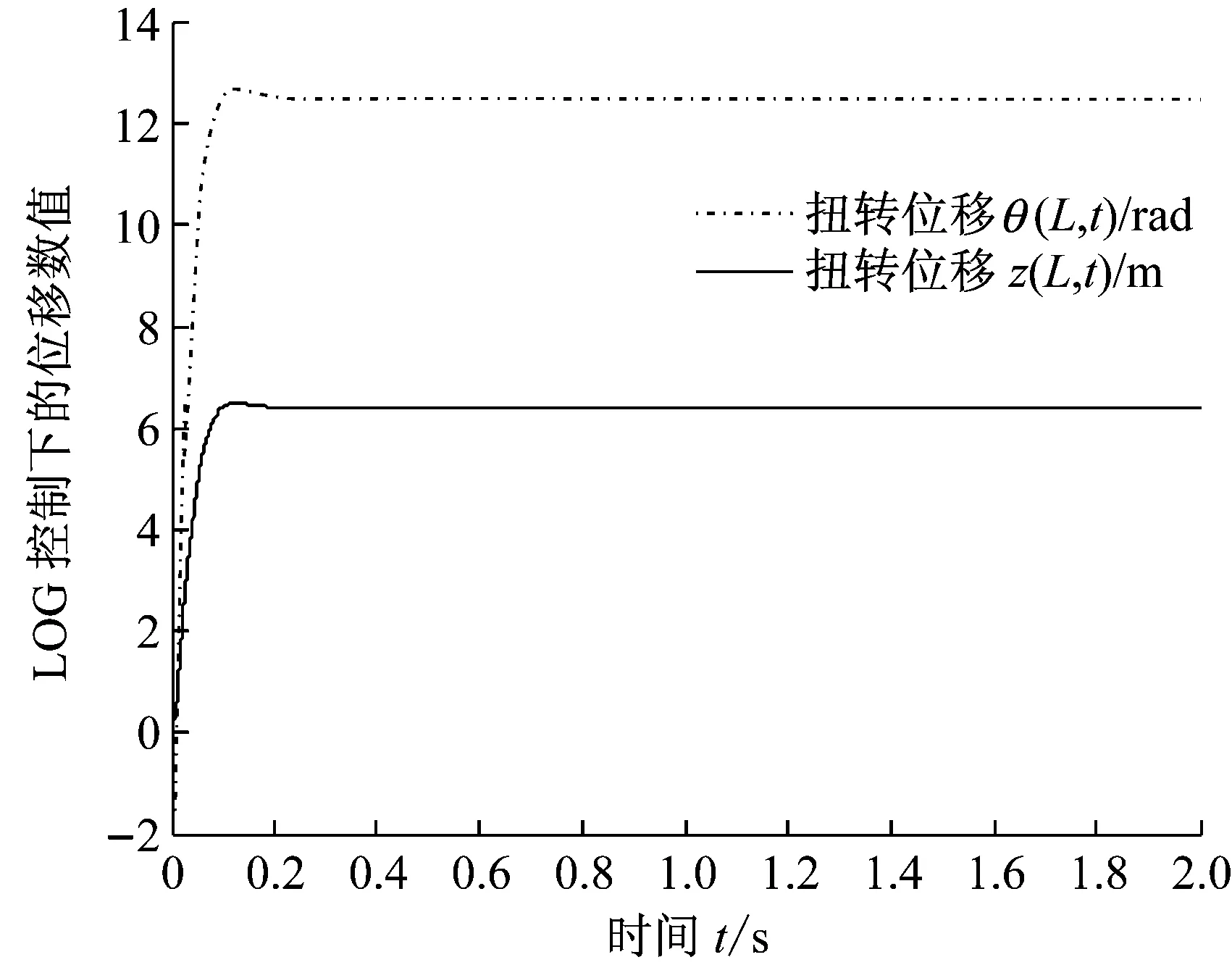
(c) LQG控制下的扭转和挥舞位移
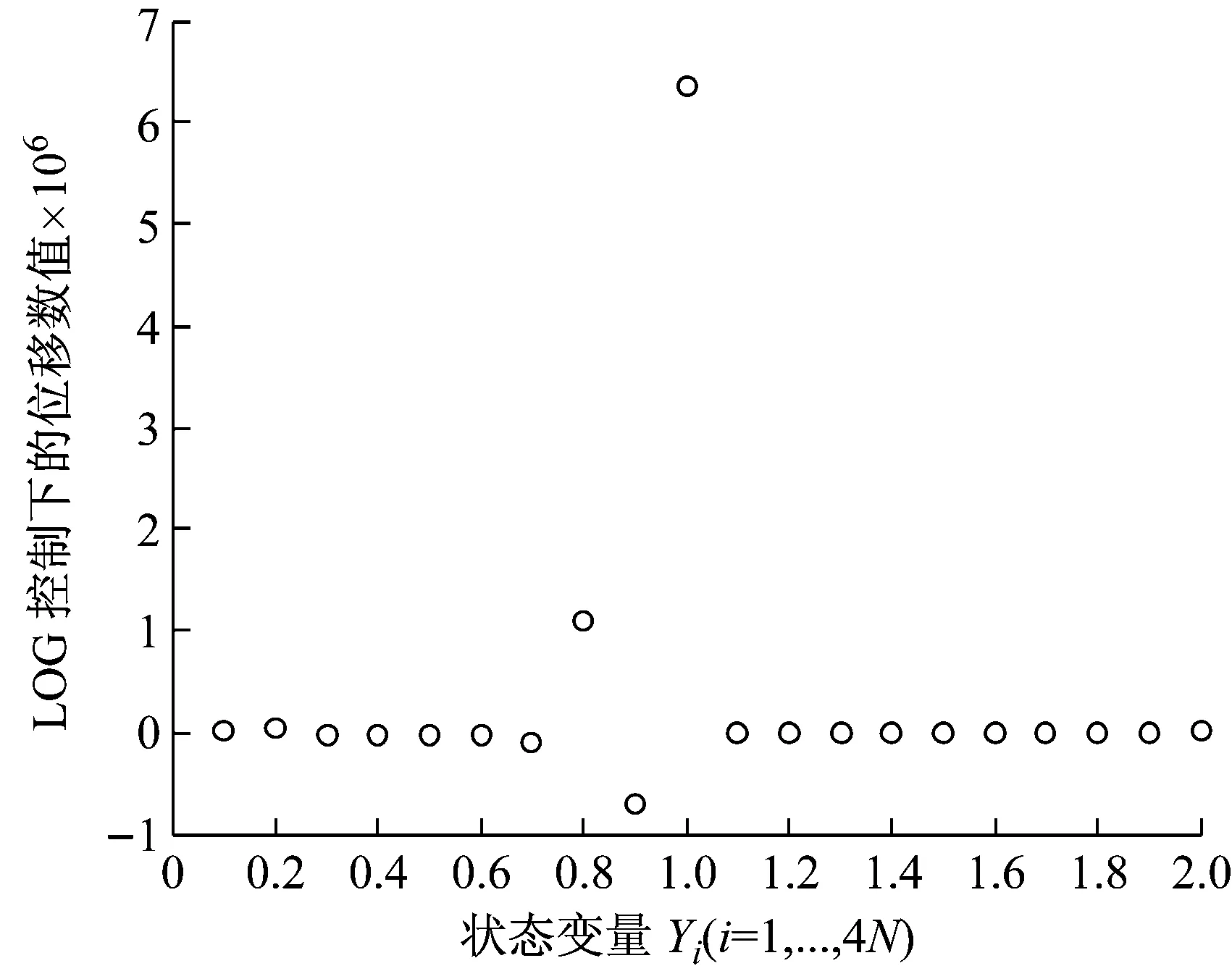
(d) LQG控制器的响应幅度
3.1 输入端回路传输恢复LLTR控制结果
图4(a)和(b)展示了输入端回路传输恢复LLTR控制下的扭转和挥舞位移。与图3(c)的LQG控制下的位移相比较,虽然有3 s内的波动,但无论从仿真角度还是工程实际角度,都是真正收敛的,而且最大幅度大大减小,正体现了折中控制的结果。
图4(c)为输入端LLTR对扭转和挥舞的控制器响应,其幅度很小且波动非常平稳,控制能量需求稳定,且能有效避免控制器硬件冲击。控制器本身的内部稳定,才能真正保证系统的内部稳定,而适合于实际工程应用。
图4(d)展示了4N+1条控制器的奇异值(Singular Value, SV)伯德图曲线:所有曲线几乎重叠,无渐进过程,体现了输入端回路传递函数的曲线能足够地快速接近直接状态反馈的结果,最大限度保证了所设计控制器效果的合理性。且SV值全部小于零,体现了很好的干扰抑制性能和良好的跟踪输入参考信号的能力;中高频部分斜率变化较大,体现了较好的高频突变噪声的抑制能力,正好可与临界失速状态的噪声突变相适应。
3.2 输出端回路传输恢复LLTR控制结果
在前述基本参数下,图5(a)和(b)展示了输出端回路传输恢复LLTR控制下的扭转和挥舞位移的时间响应。与图4(a)和(b)的时域响应相比,幅度依然合理,总体变化趋势较为优越,低频信号较弱,但高频信号较强,特别是图5(a)的扭转出现了极限环振荡状态,随着时间推移出现等幅振荡,不过等幅振动部分幅度较小,处于可控的合理范围,但高频波动幅度较大,有较大频率混叠。
图5(c)的控制器综合响应仍然合理,属于可操作范围。图5(d)的奇异值伯德图曲线依然小于零且幅度更大,体现了良好的干扰抑制能力,而且波动平稳,体现了良好的噪声抑制能力,但奇异值增益较小,对波动突变较大的高频噪声的抑制能力不足(这也可能是扭转位移出现高频极限环的原因)。同时4N+1条控制器的奇异值曲线并不重复,渐进接近直接状态反馈的结果,故图5(c)的控制器初始响应并不光滑和平稳。
从图4、图5的对比可知:输入端LLTR控制能很好地抑制突变高频噪声,但对低频干扰抑制较弱;而输出端LLTR则能更好地抑制低频干扰,而对高频突变噪声抑制能力较弱。无论从被控对象的最大振动幅度还是控制器的最大响应幅度看,两种方法都属于可控范围,与LQG控制器相比,具有非常明显的工程应用优越性。
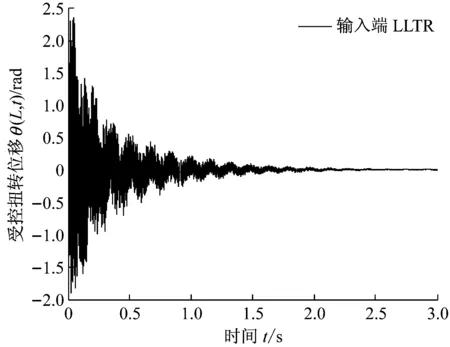
(a) 输入端LLTR控制的扭转位移
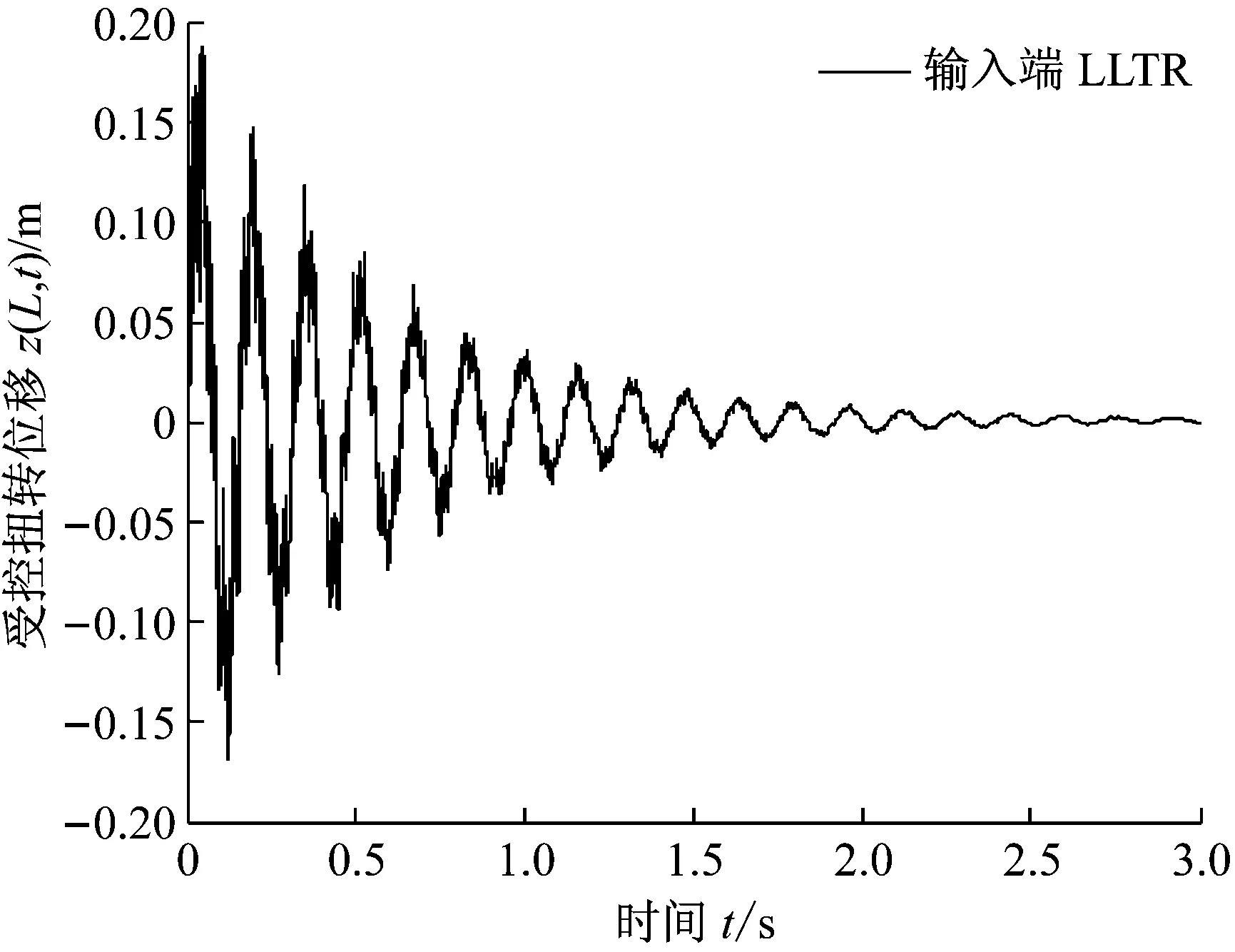
(b) 输入端LLTR控制的挥舞位移
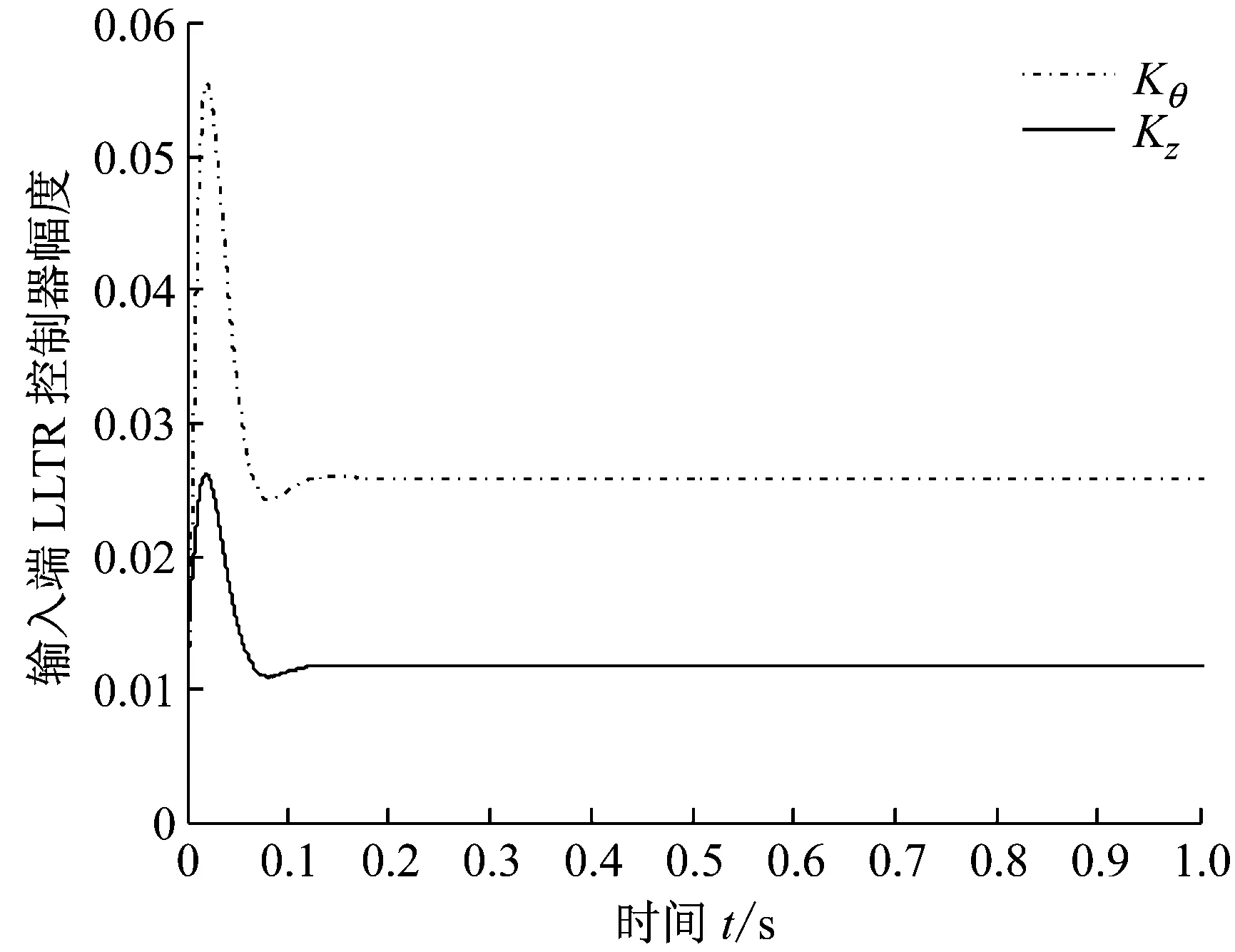
(c) 输入端LLTR控制器对扭转和挥舞的综合响应幅度
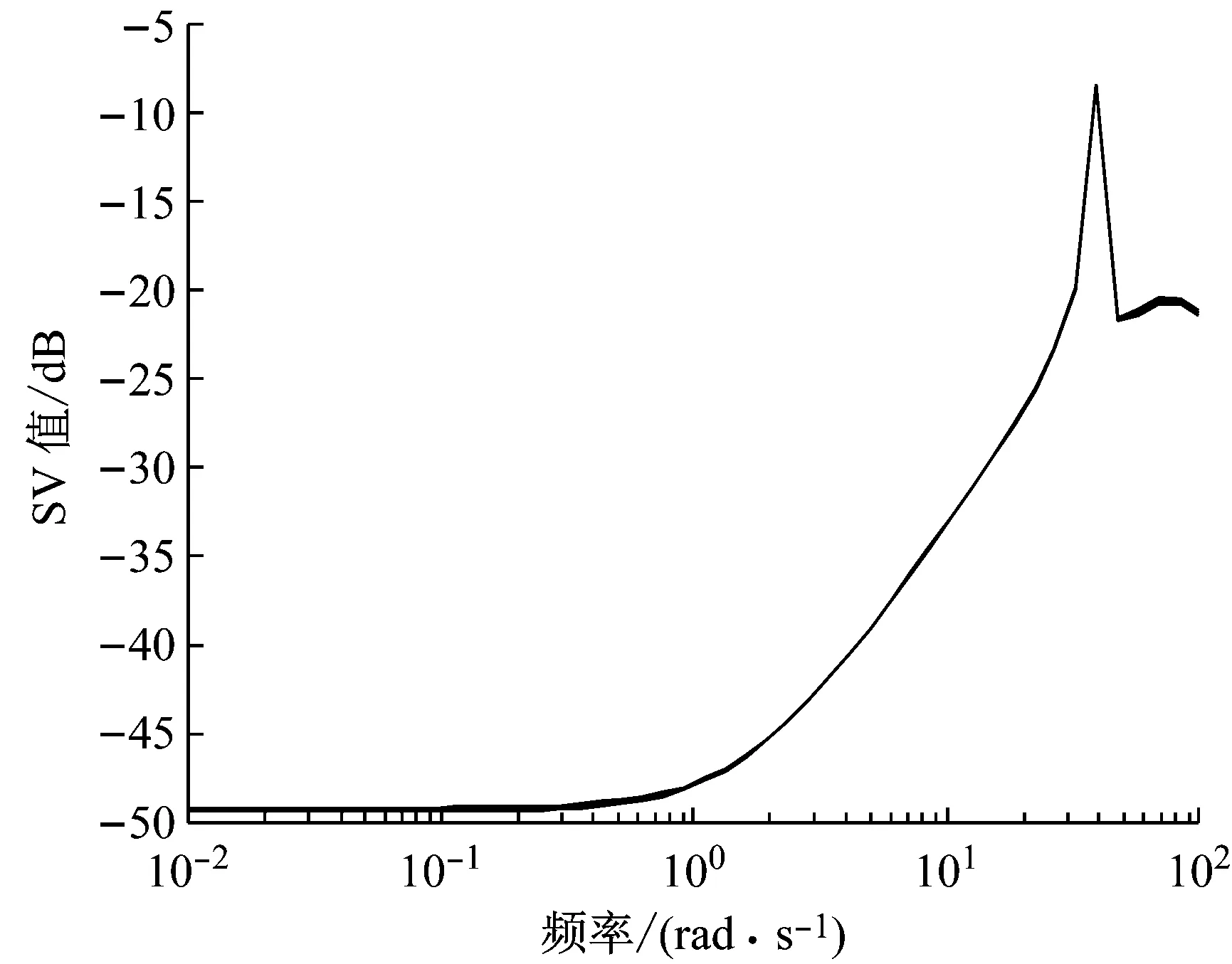
(d) 输入端LLTR控制的奇异值曲线
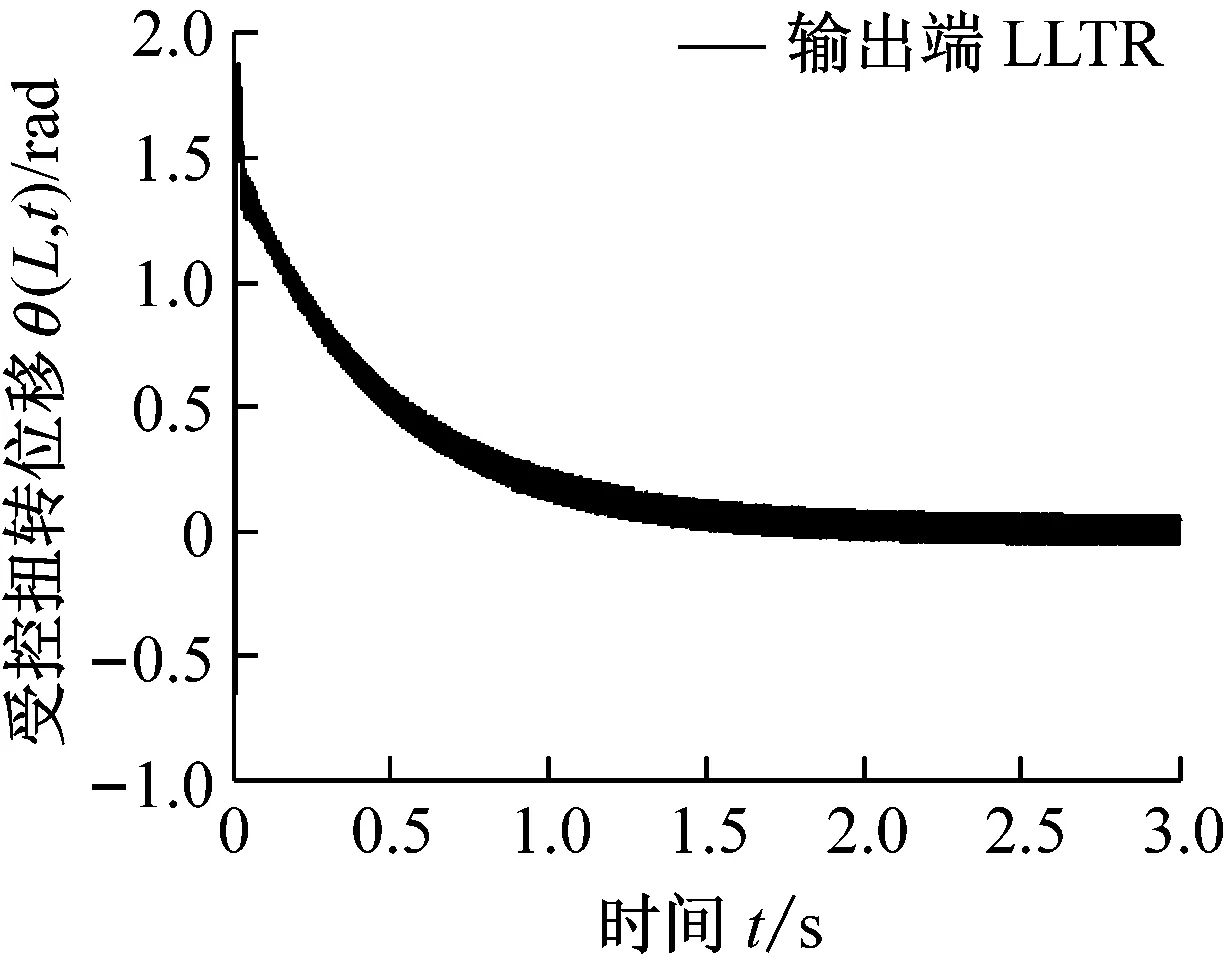
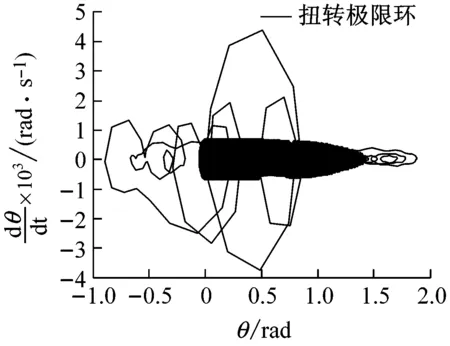
(a) 输出端LLTR控制的扭转位移及扭转极限环
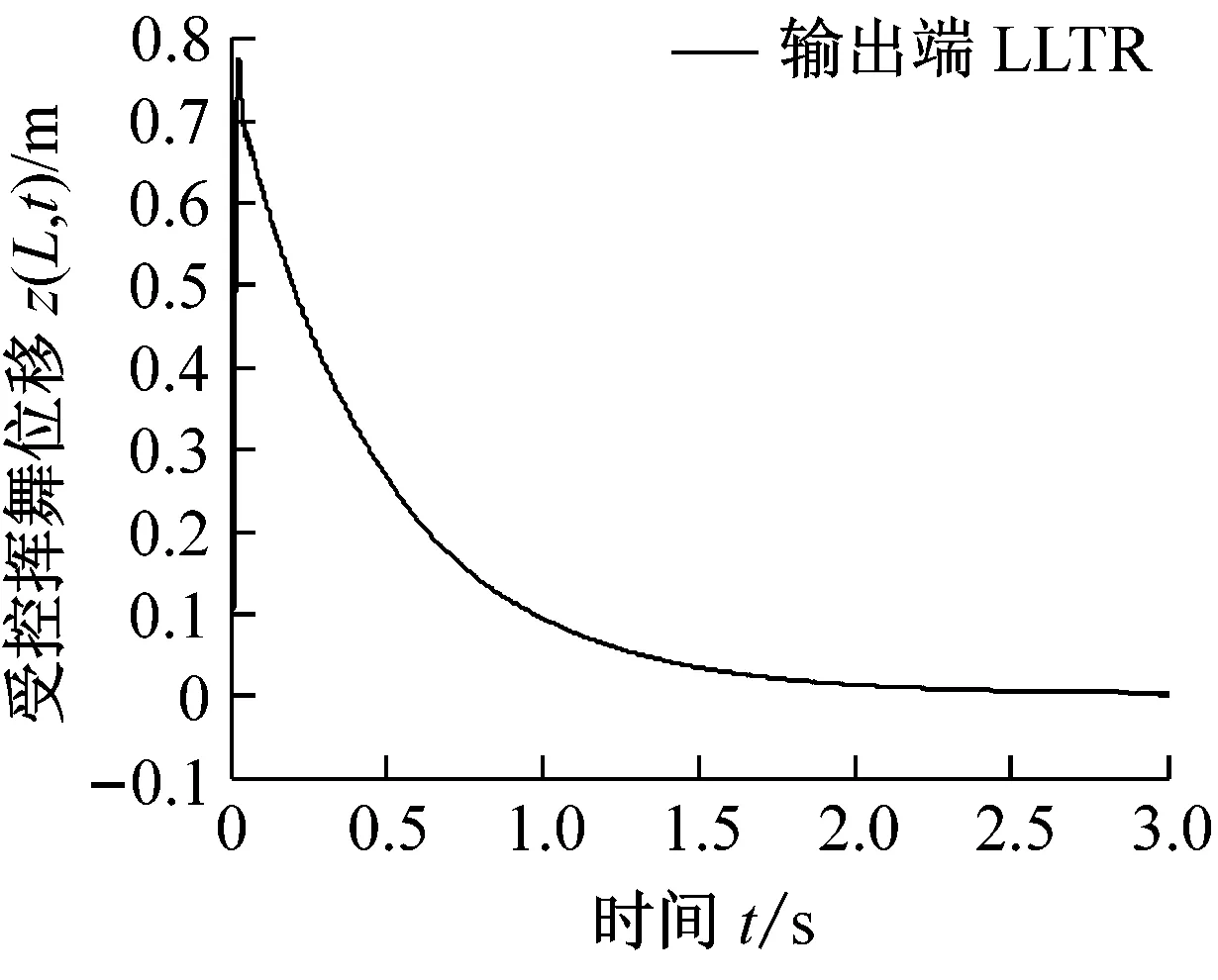
(b) 输出端LLTR控制的挥舞位移
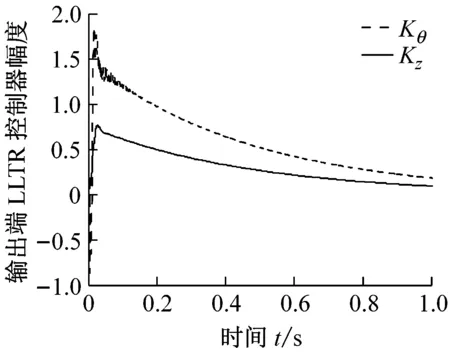
(c) 输出端LLTR控制器对扭转和挥舞的响应幅度
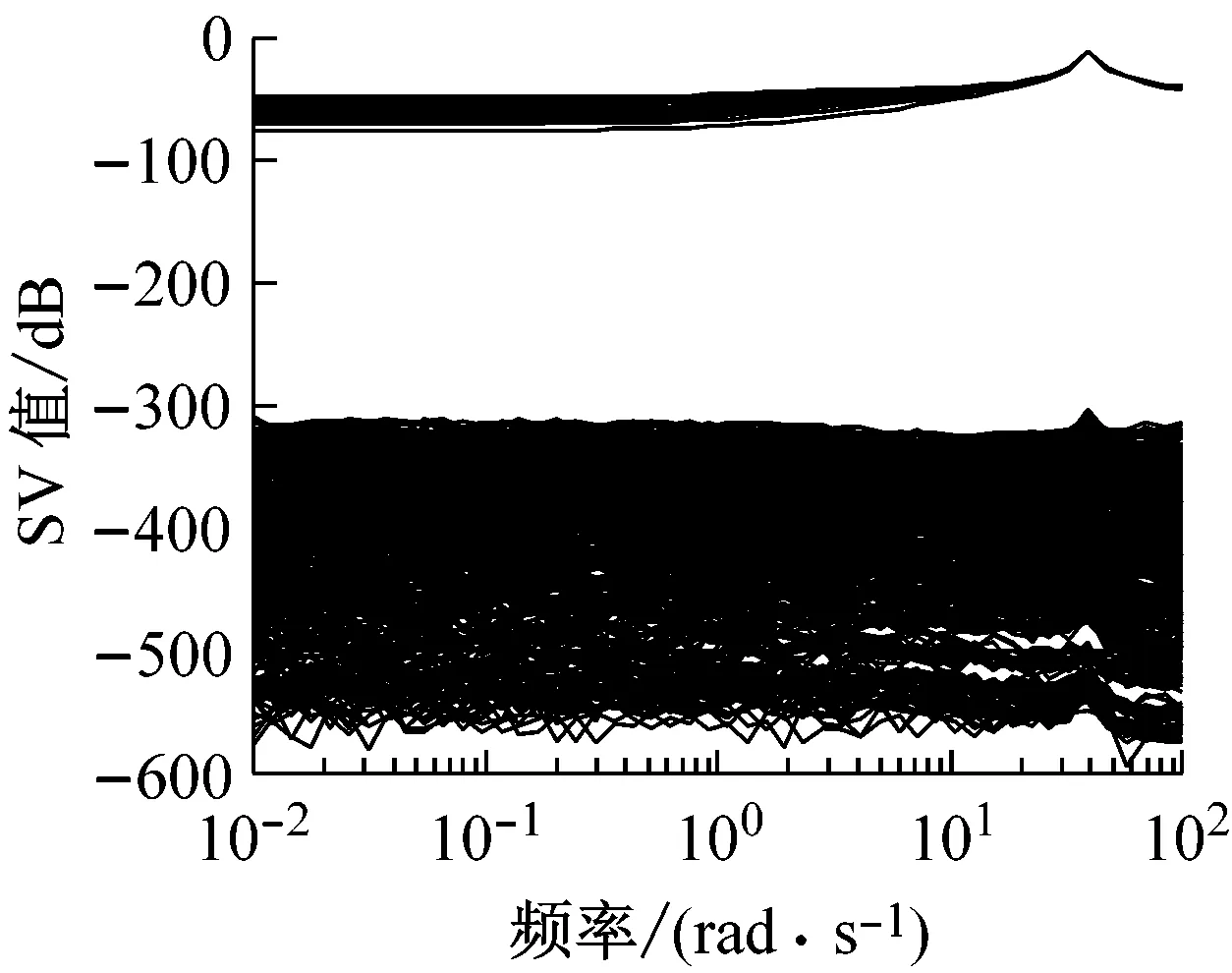
(d) 输出端LLTR控制的奇异值曲线
4 LLTR控制算法的实时效应
鉴于风洞实验测试临界状态的困难,本设计难以进行实际验证,但控制算法的有效性可以通过一种半实物仿真实验平台[16]来检验。该平台利用了一种PLC-OPC通讯技术,将气弹系统模型完全在MATLAB仿真环境中运行,被控气弹模型的输出通过PLC-OPC通讯,利用SIMULINK的“OPC Write”模块输入到PLC响应的内存中;整个LLTR控制算法的实现则完全在PLC中运行;而PLC发出的驱动信号由“OPC Read”模块输出到气弹模型。
数据的通讯过程为:首先由PC Access定义PLC的数据类型和内存区域,并连接PLC;其次,MATLAB的OPC Server定义相应的仿真部分的数据类型和内存区域,并与PC Access数据相连接;最后由SIMULINK进行读写操作。由于大型风电系统控制多采用PLC,故本设计控制器采用西门子S7-200控制器,且信号的即时显示和监控可以由连接在PLC的台达触摸屏人机界面(Delta HMI)实时显示出来,故称为半实物仿真实验平台。
通过实时验证发现:LQG实时控制的过程确实会出现控制器硬件宕机中断,或者实时效应与LQG仿真出现较大的偏差,可能由于前述LQG控制器的控制器响应幅度过大,或滤波响应过快,在PLC运行时出现了内存溢出或者数据不匹配等问题。而LLTR控制过程则展示了良好的实时效应,人机界面HMI图6,展示了输入端LLTR控制下的扭转位移和挥舞位移的实时效应,包括实时曲线和实时数值,与前述图4(a)和(b)仿真结果相比,体现了良好的一致性。由于前述仿真为自动变步长仿真,采样时间非常小,而实际的控制器硬件的采样间隔为定常有限值,故曲线的波形有所区别,但变化的幅度和趋势相当一致。
另外需要特别说明的是:在仿真中向量q的最大量级可以取至1010,仿真结果非常理想(继续增大会引起截断误差而使得仿真结果变差),但在实时控制验证中,这一量级仍然显得太大,会出现前述数据不匹配的问题,而在102量级时完全可以通过控制器硬件验证。这也正是本设计进行控制算法实时验证的另一原因所在。
(a) 主界面
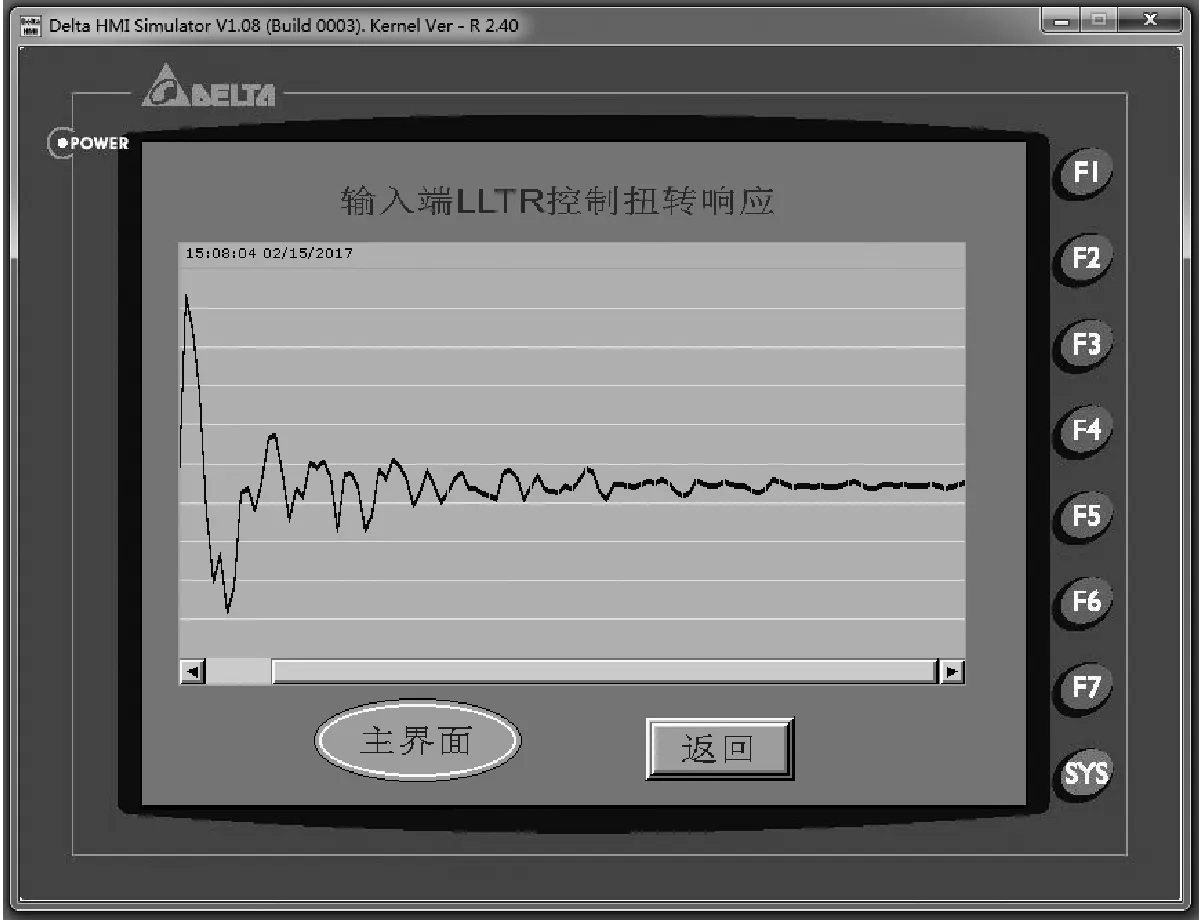
(b) 输出端LLTR控制的扭转实时效应
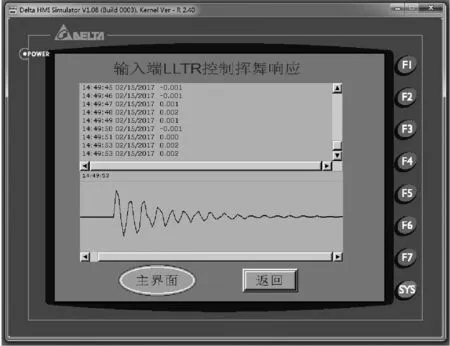
(c) 输出端LLTR控制的挥舞实时效应
5 结 论
(1) 从前向飞行直升机叶片借鉴并修正了一种准稳态气动力,用于风力机叶片的准稳态响应分析和控制,为极端风速下风力机叶片临界颤振状态的研究提供了一种思路。
(2) 基于输入端回路传输恢复和输出端回路传输恢复两种LLTR控制过程,进行了发散不稳定控制。分别通过扭转/挥舞时域响应分析、控制器时间响应分析、及奇异值伯德图曲线的对比,论证了两种方法的区别。两种LLTR控制方法均体现了相对于LQG控制的工程应用优越性,可以根据实际情况折中选择。
(3) LLTR控制算法的有效性通过半实物仿真实验平台的实时效应得到了验证。半实物仿真平台不仅能够佐证不同控制算法性能的优劣,而且可以检验同一算法中参数取值范围的合理性。该半实物仿真实验平台也为同类项目控制算法的有效性研究提供了一种可行性方案。
