考虑边缘效应的MEMS梳齿谐振器的静动力学特性分析
2018-08-01马贺冲张琪昌
马贺冲, 张琪昌, 陈 涛, 李 磊
(1. 天津大学 机械工程学院天津市非线性动力学与混沌控制重点实验室, 天津 300072; 2. 内蒙动力机械研究所, 内蒙古 010010)
MEMS谐振器是一种高精度的微机械电子元件,是利用谐振器内部振子的机械谐振特性来进行工作,性能十分稳定,广泛用于航天航空、生物技术、精密测量、国防军事、通讯等领域,由其产生的静动力学问题也逐渐成为当前国内外的研究热点[1-2]。梳齿式谐振器是微谐振器中较为常见的结构,整体为硅材料,采用非接触式激励和检测,易获得高灵敏度,相对于梁式结构更加稳定,具有效率高、精度高、激励形式多样等优点并被广泛应用到滤波器、加速度传感器、光频梳和能量采集器等众多产品中[3]。研究静电驱动梳齿谐振器的振动特性,不仅能够提高研究人员对梳齿谐振器的静动态特性的了解,而且对于MEMS 结构的优化设计也具有一定的参考价值。
梳齿结构的动力学态特性问题一直以来受到研究者的重点关注。Nguyen等[4]对梳齿驱动器的振动特性进行了实验分析,其实验结果得到了广泛认可。Elshurafa等[5]建立了微梳齿折叠梁的振动模型并对其软硬特性进行研究,讨论了系统软硬特性的区分标准。Han等[6]分析了梁式谐振器线性振动情况下系统最优直流电压与等效固有频率的参数表达式并讨论了物理参数对于该行为的影响。Zhong等[7]研究了微梳齿结构的齿状结构的形状对结构动力学特性的影响,得出以下结论:倾斜梳齿可以减小系统的软化行为,导致频率的偏移,增强微谐振器的振动稳定性,并避免吸合效应的发生。张峰等[8]分析了静电梳齿结构结构稳定性随支撑梁结构参数的变化关系,并采用有限元仿真软件对计算结果进行了验证。
静电激励力是研究MEMS动力学的基础,准确计算MEMS静电激励力是合理准确地分析MEMS振动特性的前提条件。目前梳齿结构静电力的计算大多基于无限大平行板模型[9],但实际上由于梳齿本身的结构特性,其静电力存在明显的边缘效应。Dong等[10]对梳齿结构的静电力进行了模拟仿真,结果表明边缘效应会导致梳齿结构静电力明显增大。高世桥等[11-12]推导了梳齿结构静电力基于边缘效应的数学模型,并对比了与无限大平行板模型的差别,但并未进一步研究边缘效应对梳齿谐振器动力学行为的影响。Elshurafa等建立了梳齿驱动器的静电力模型,但并未对梳齿横向的静电力进行准确分析。
因此,目前的文献中并没有对边缘效应下MEMS梳齿结构的振动特性进行系统性研究。本文采用最小二乘法对微梳状谐振器的复杂静电力形式进行拟合,并采用多尺度法进行求解,简化了梳齿结构的复杂动力学问题。笔者对梳齿谐振器采用理论分析,并回归到物理参数分析不同参数下梳齿折叠梁动态行为,这对于梳齿结构的优化设计具有指导意义。
1 静电激励力分析
图1为典型MEMS梳齿谐振器模型图,主要由固定梳齿,可动梳齿,锚点,折叠梁等结构组成。其中,梳齿部分与电极相连,形成平行板电容结构并产生静电力,驱动电压为Vdc和Vaccos(Ωt)。设梳齿结构所含梳齿个数为N,系统的总静电力为单个平行板电容器静电力之和。可动梳齿与固定梳齿尺寸完全相同,x0为可动梳齿与固定梳齿之间的间隙,w为梳齿齿宽,h为梳齿厚度(垂直纸面方向),a为可动梳齿与固定梳齿间的重叠长度,d为相邻齿间距离。由于系统为对称结构,故只研究沿x方向的运动。设Ct和Cl分别为梳齿结构横向和纵向电容,Ft和Fl分别为梳齿横向与纵向电容产生的沿x方向的静电力。另外,W为折叠梁的宽度,L折叠梁长度,可动梳齿等效质量为m,品质因子为Q,弹性模量为E。
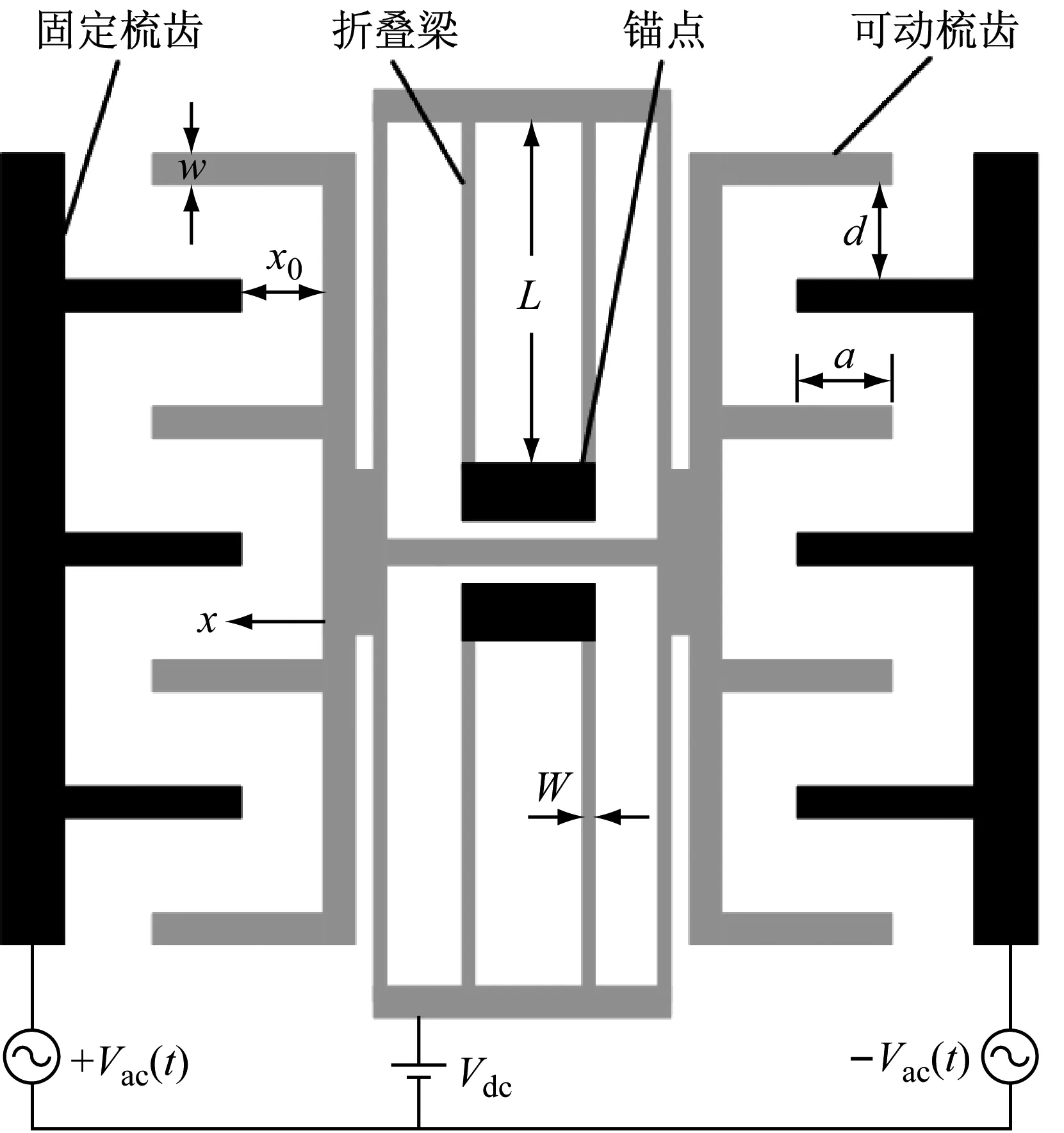
图1 MEMS梳齿谐振器模型图
1.1 单侧静电激励力
由图1可知,系统沿x方向的静电力包括横向电容产生的静电力和纵向电容产生的静电力。首先对梳齿结构的横向静电力进行研究。赵剑等[13]对平行板电容产生的静电力场进行模拟仿真,发现平行板间距与宽度的比值越大,边缘效应对电容的影响越明显。同时因为梳齿结构都采用高纵深比的工艺加工,齿宽相对梳齿间距要小很多,所以边缘效应对梳齿结构横向静电力影响很大,因而不能把梳齿结构看作无限大平行板模型进行处理分析。结合姚峰林等给出的梳齿横向电容在边缘效应下的计算公式,设固定梳齿与可动梳齿间的驱动电压为Vdc+Vaccos(Ωt),梳齿结构沿x方向的整体横向电容可以表示为
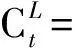
(1)
可求得则单侧整体的横向静电力为
(2)
令
得
(3)
(4)
梳齿结构同时受到纵向电容产生的静电力的影响,由已有研究[14]可推导出梳齿结构在边缘效应下纵向电容为
(5)
其中
则纵向静电力系数为
(6)
1.2 总静电激励力
工程应用中梳齿谐振器一般采用双边激励的形式,使结构两端都受到静电力的作用,如图1所示。梳齿谐振器的工作原理是,在可动极板与固定极板间施加直流电压,在结构两两侧施加大小相同,方向相反的交流电压,在静电力的作用下,可动梳状电极向固定电极方向运动,使中间的折叠梁发生变形,然后带动其他元件的运动。由已有研究可知系统总静电激励力为
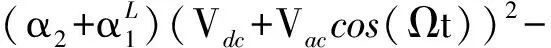
(7)
其中
(8)
将式(7)展开,因为Vdc>>Vac可忽略高阶激励项可得到
(9)
2 运动方程与振动响应方程
选取梳齿结构折叠梁为研究对象, Silva等[15]将折叠梁看作铁木辛柯梁模型进行了简化处理,之后Elshurafa AM推导出了折叠梁的单自由度Duffing方程,梳齿谐振器动力学方程如下
(10)
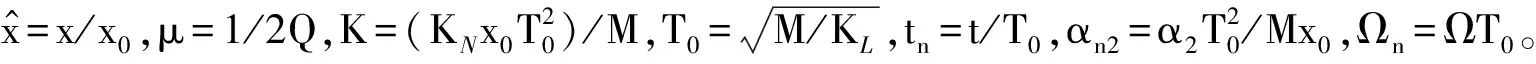
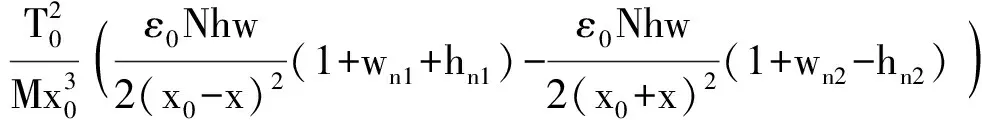
(11)
其中
(12)
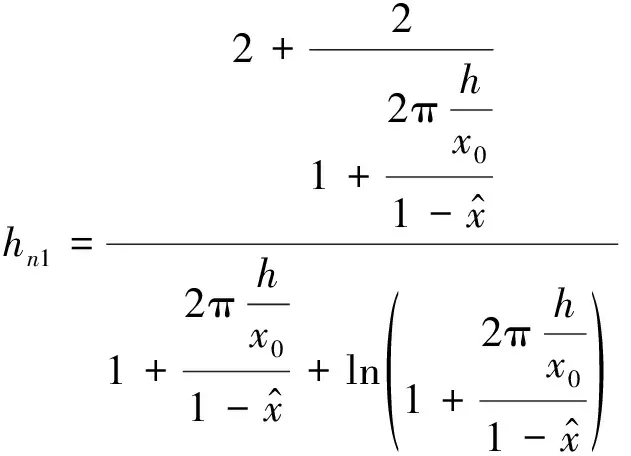
(13)
(14)
(15)
单自由度微梳齿结构的无量纲化的方程表达为
(16)
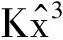
由αn1形式可得,边缘效应下的横向静电力比无限大平行板模型下的横向静电力要大。为了研究边缘效应对系统动力学行为的影响,将考虑边缘效应和不考虑边缘效应下的αn1进行对比分析,如图2所示。
当x0=16 μm时,从图2中可以看出,随着偏移距离的增大,αn1逐渐增大,边缘效应模型与无限大平行板模型横向静电力的差值越来越大,相对差值越来越小。根据之前的分析可以得到一个定性的结论:在梳齿结构中边缘效应会导致系统静电力明显增大,从而增强系统的软化效应。这一结论是对以上分析结果作出的定性判断,如要进一步研究还需要对原始系统进行深入分析。
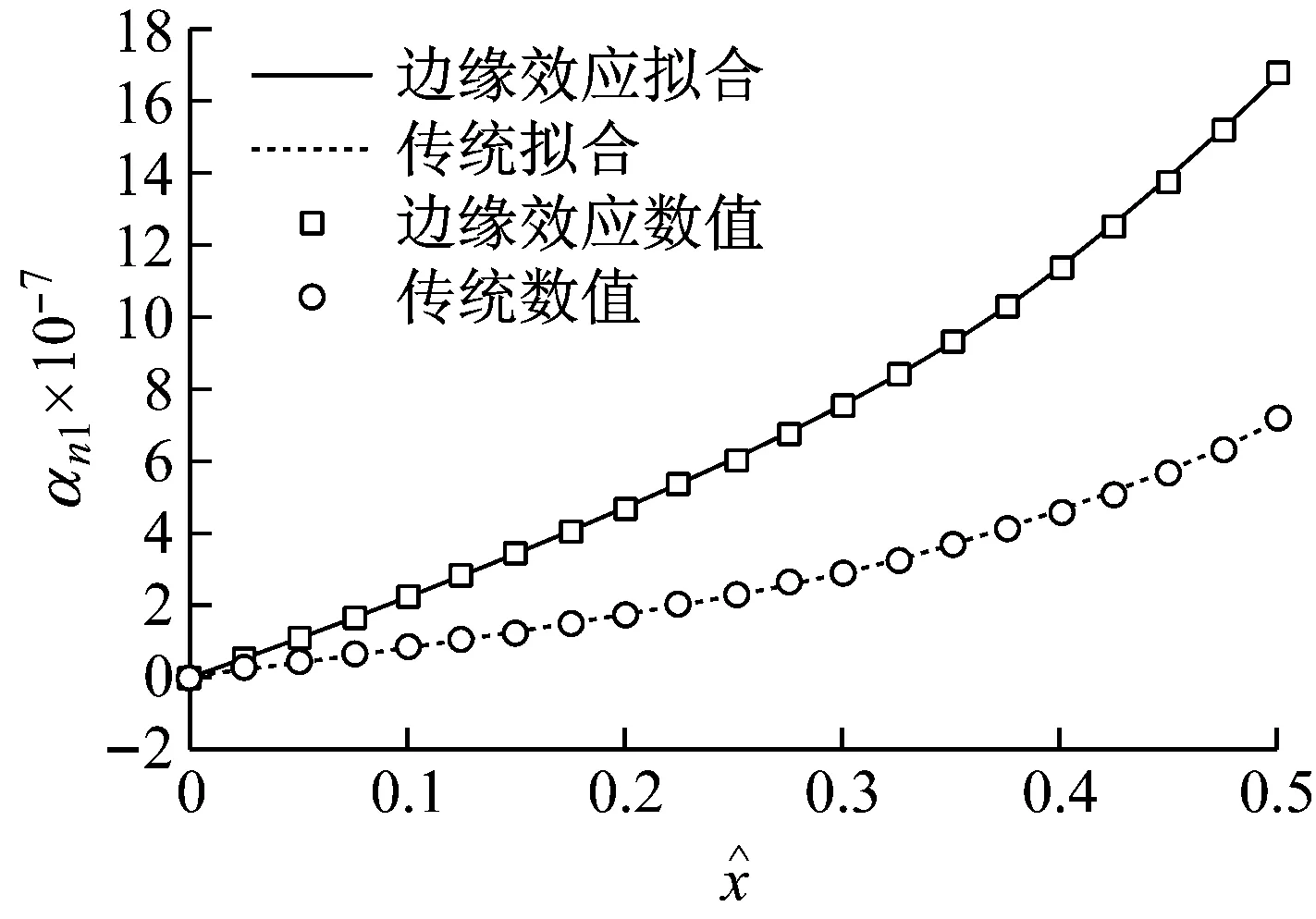
图2 静电力系数图
因为αn1形式十分复杂,导致式(16)无法直接解析,因此难以对梳齿结构的振动特性作进一步研究。本文采用最小二乘法对梳齿边缘效应下静电力进行拟合,设
(17)
由图2可以知道,最小二乘的拟合结果与原曲线十分接近,并且偏移距离越小,最小二乘法的拟合结果越好。将式(17)代入式(16)得到
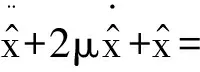
(18)
使用多尺度法[16]对式(18)进行求解可得
(19)
其中σ=f/f0-1,f是激振频率,f0=1/(2πT0)。An=A/x0,A代表谐振器振幅。此外,主共振峰值及脊骨线的表达式可分别表示
(20)
(21)
由式(20)可知系统的最大幅值与纵向静电力系数α2相关。边缘效应模型比平行板模型的振幅大,边缘效应大小与梳齿形状有关。虽然α1较α2小很多,但由于直流电压远远大于交流电压,所以横向电容产生静电力往往大于纵向电容产生的静电力。因此本文主要对边缘效应下梳齿横向静电力对系统动力学特性的影响进行研究。
3 理论分析与数值仿真
3.1 边缘效应对系统横向稳定性的影响
在微梳齿谐振器的工作过程中,交流电压远远小于直流电压,同时由于处于近似真空的工作环境中,谐振器有很高的质量因子,因此在分析中可以将阻尼与交流电压看作是对系统的扰动。在这里考虑无扰动下的保守系统,可以得到无量纲动力学方程所对应的Hamilton 方程如下
(22)
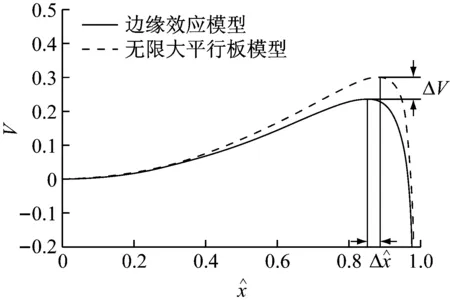
图3 保守系统势能曲线图
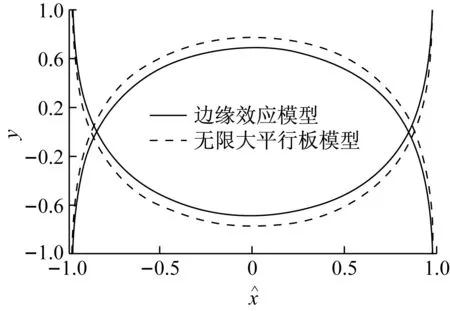
图4 保守系统相空间流形
通过Hamilton 方程可以画出系统的势能图。从式(22)可以得到,无量纲参数K和αn1共同确定了该保守系统的势能函数的具体形式。选取一组典型参数下的势能图(图3)和同宿轨道图(图4),根据图3和图4的结果可以得到,边缘效应模型与无限大平行板模型的不稳定平衡点的位置与峰值不同,边缘效应模型与普通模型相比,所对应的稳定平衡点与不稳定平衡点之间的距离偏小。进而得出结论:边缘效应下的势垒更加接近势阱,同时外部势垒能量降低,同宿轨道包围的稳定区域逐渐减小,这一变化一方面减小了谐振器的动态可行域,另一方面也增加了谐振器发生吸合的概率。
3.2 边缘效应对系统固有频率的影响
在交流电压与阻尼的微小扰动作用下,系统的振动以小幅运动为主。研究主共振情况下谐振器的动力学行为对梳齿谐振器的动态设计与应用有一定的参考价值。单独研究无量纲参数下系统的动态行为,虽然能够对系统的动力学特性有较为系统的认识,但通过方程推导可知,无量纲参数之间并不是相互独立的,而是通过有量纲物理参数相互关联的,无量纲分析的最终结果须返回到物理参数模型中,这样才能将理论分析与实际问题相结合,对实际生产和设计予以指导。为此,本节以某一具体的梳齿模型为例来研究物理参数下此类谐振器的动态特性。微梳齿的主要结构参数以及材料参数如表1 所示。微谐振器一般是利用振子的主共振原理工作的,因此,研究主共振情况下的线性与非线性振动特性对于掌握此类微谐振器的动态行为具有一定的理论与实际意义。
由式(21)可以得到系统等效固有频率
(23)
在已发表的梳齿谐振器的相关文献中,Nguyen和Howe的实验结果得到了广泛认可,而Khirallah[17]则做了许多理论仿真研究工作。他们的实验和理论研究结果均一致表明,随着直流偏置电压逐渐增加,系统的谐振频率将会逐渐降低。图5反映了不同初始间距的情况下,系统固有频率随直流电压的变化情况。MEMS梳齿谐振器的固有频率的变化情况与Nguyen得到的实验结果一致,随着直流电压的增大而逐渐减小。在不同初始间距下,随着电压的增加,系统固有频率的衰减情况不同,间距越小固有频率随电压衰减速度越快。边缘效应模型明显比无限大平行板模型的衰减速度更快,可知边缘效应能够引起系统谐振频率的偏移。MEMS 设计人员需要权衡谐振频率与电压输入之间的关系,根据实际需要进行动态设计。
3.3 边缘效应对系统软硬特性的影响
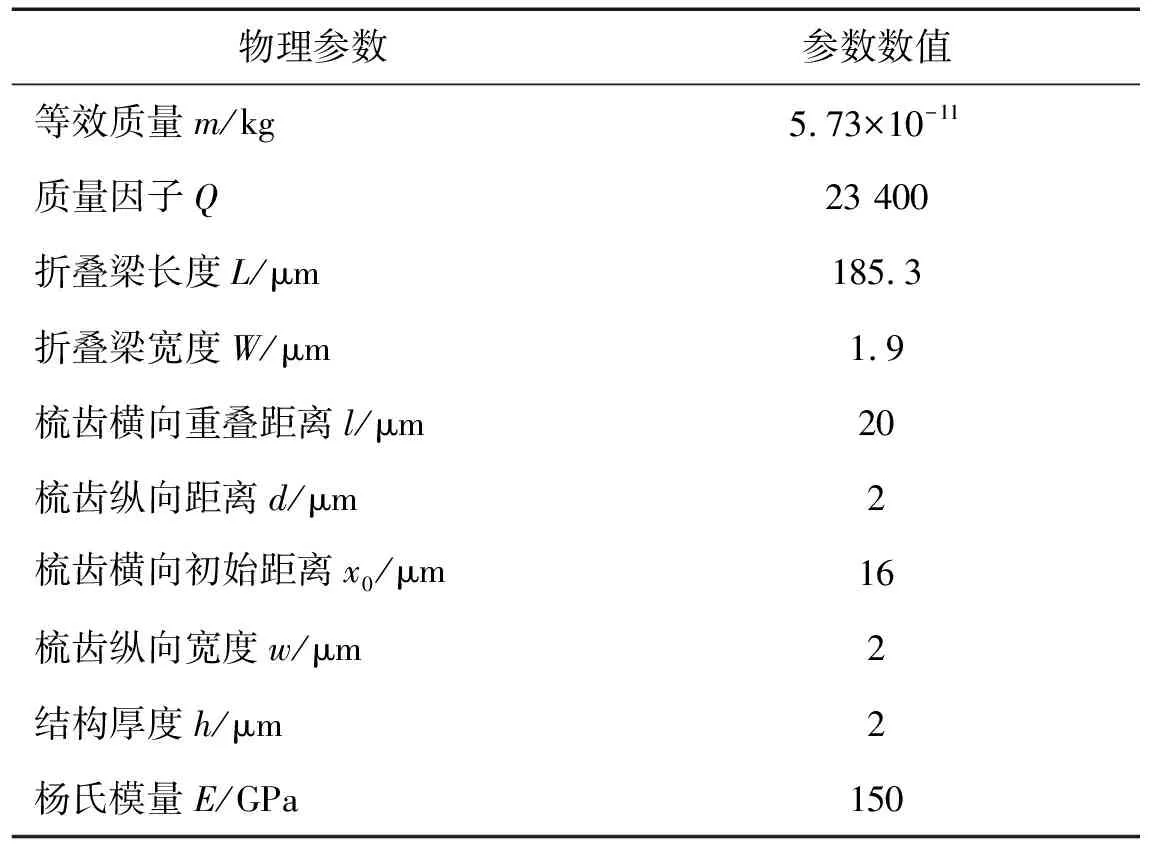
表1 微梳齿结构物理参数
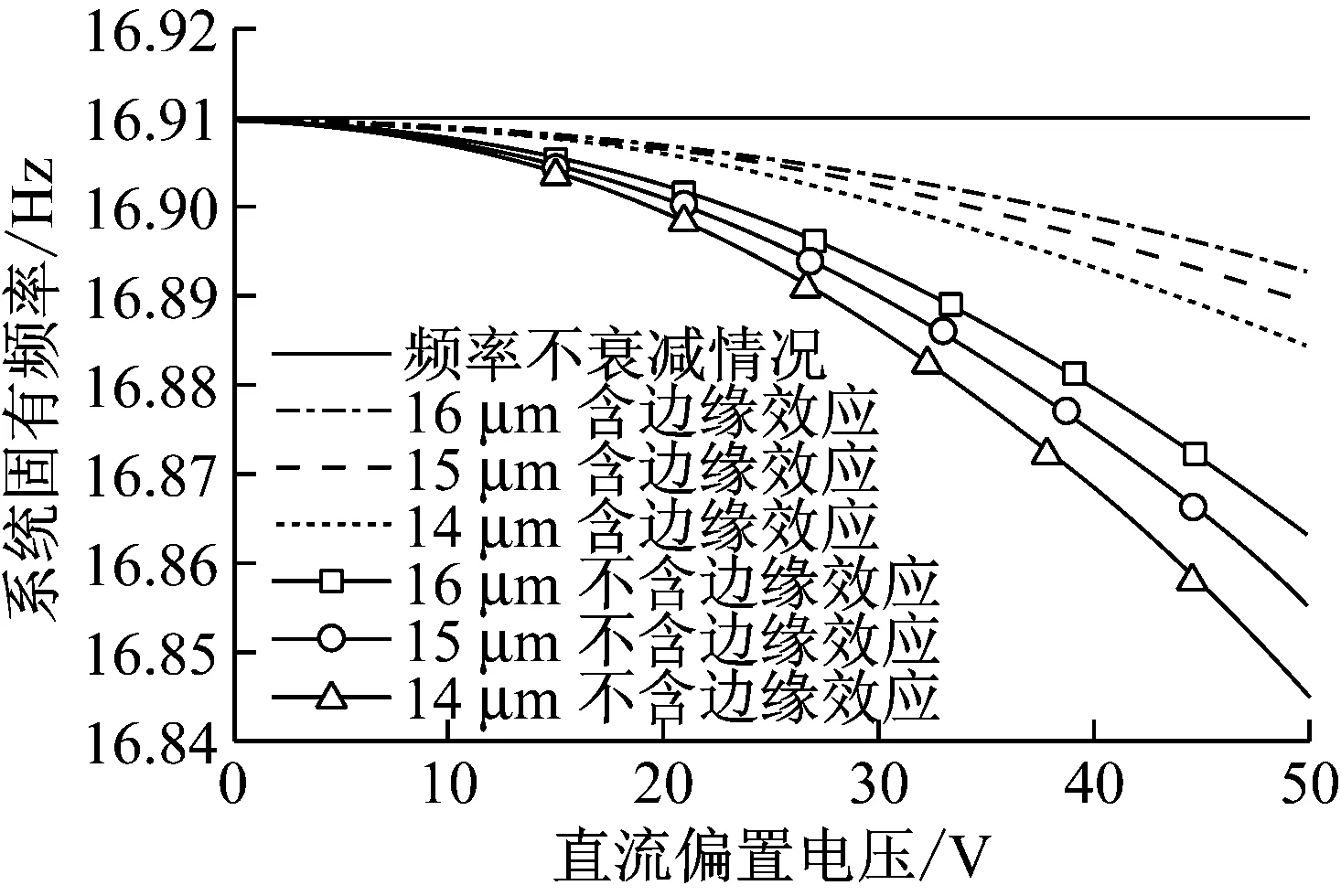
图5 系统固有频率随直流电压变化图
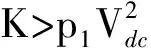
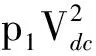
图时谐振器的幅频曲线
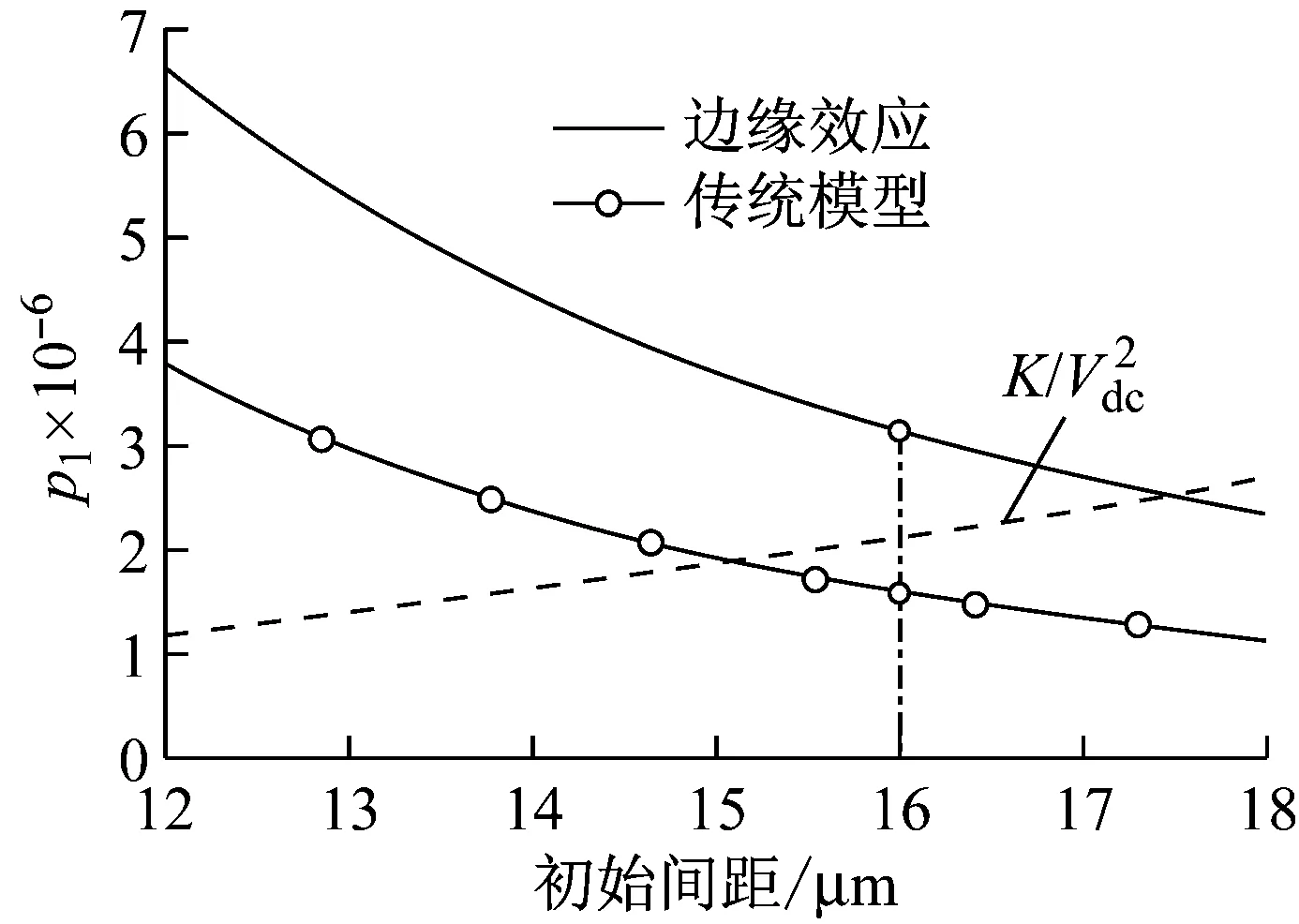
图7 p1随微梳齿初始间距变化图

图8 Vdc=30 V时谐振器的幅频曲线
3.4 边缘效应对系统线性过渡行为的影响
共振是谐振器最基本的工作特性,由但于制造工艺的原因,经常存在制造误差,导致系统的固有频率发生偏移。由前文可以知道梳齿结构的振动频带特别窄,因而必须保证电压的激振频率在系统的共振频带之内,才能更好地输出能量。由于材料属性本身很难控制,不同的材料,其密度、泊松比、特征尺度、弹性模量等都会不同,某一尺寸参数的变化也经常引起其他参量的连锁变化,导致很难对梳齿结构进行动态分析。因此要想对梳齿结构进行优化设计,应尽可能的使控制参量的影响单一化,其中电压和梳齿间距与其他参数相比具有易于控制,耦合性小的特点,所以通过改变梳齿初始间距,直流电压和交流电压,来控制系统的共振频率更加容易实现。
由式(21)和(23)可得线性过渡情况下的最优设计电压(单位:V)与等效固有频率(单位:Hz)的表达式
(24)
(25)
根据式(24),(25),可以得到不同初始间距下的线性过渡的最优设计电压与对应等效固有频率不同。系统的最优频率,由静电力拟合项和无量纲刚度系数共同决定。梳齿结构边缘效应模型的p1值比无限大平行板模型下的p1值要大得多,因此边缘效应下系统到达线性过渡临界电压值要比无限大平行板模型要小得多。图9为不同初始间距下的最优设计电压与对应等效固有频率的设计曲线,从图中可以看出,随着初始间距的增大,设计电压逐渐增大,对应的等效固有频率逐渐减小。
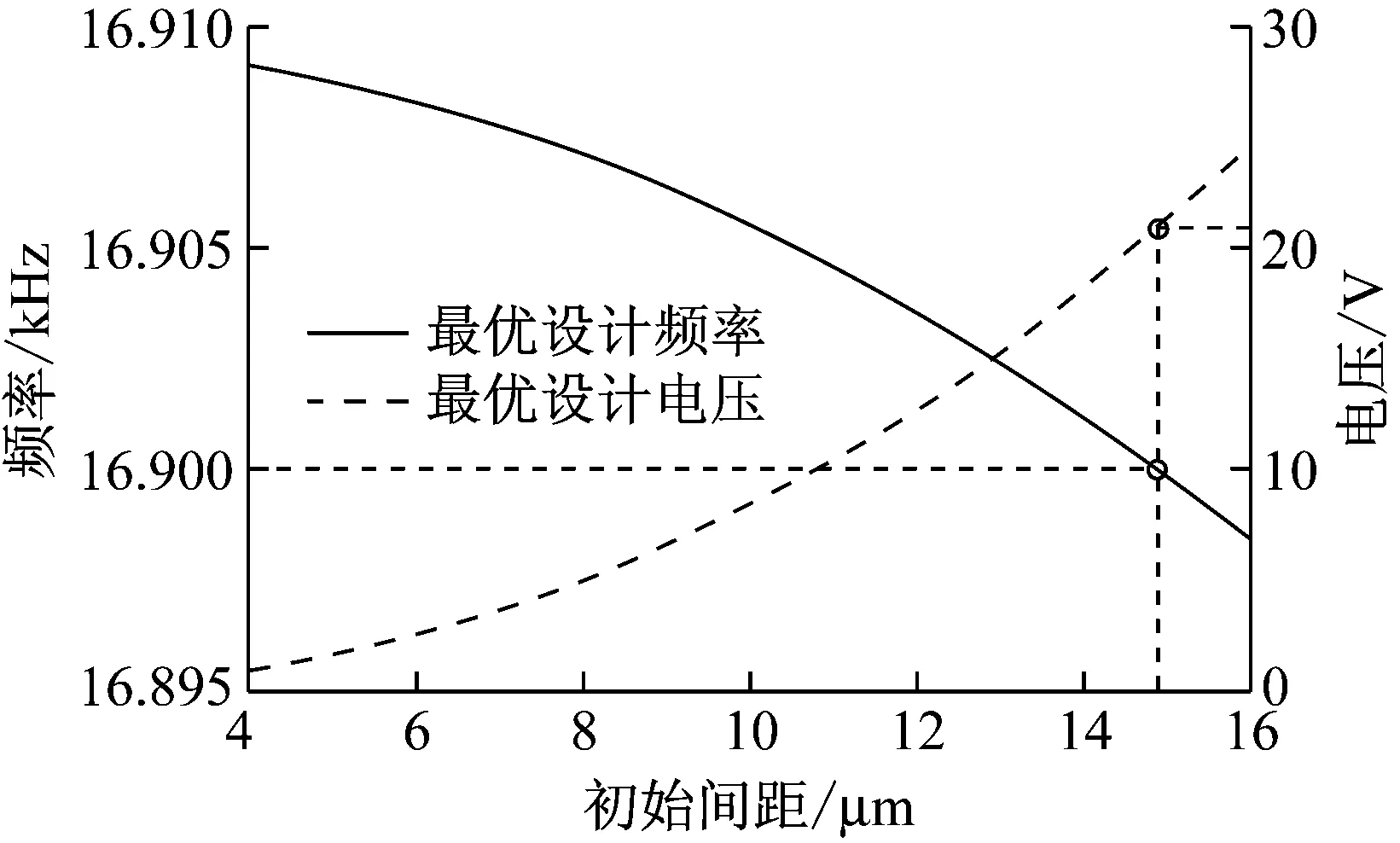
图9 最优设计电压与对应的等效固有频率曲线
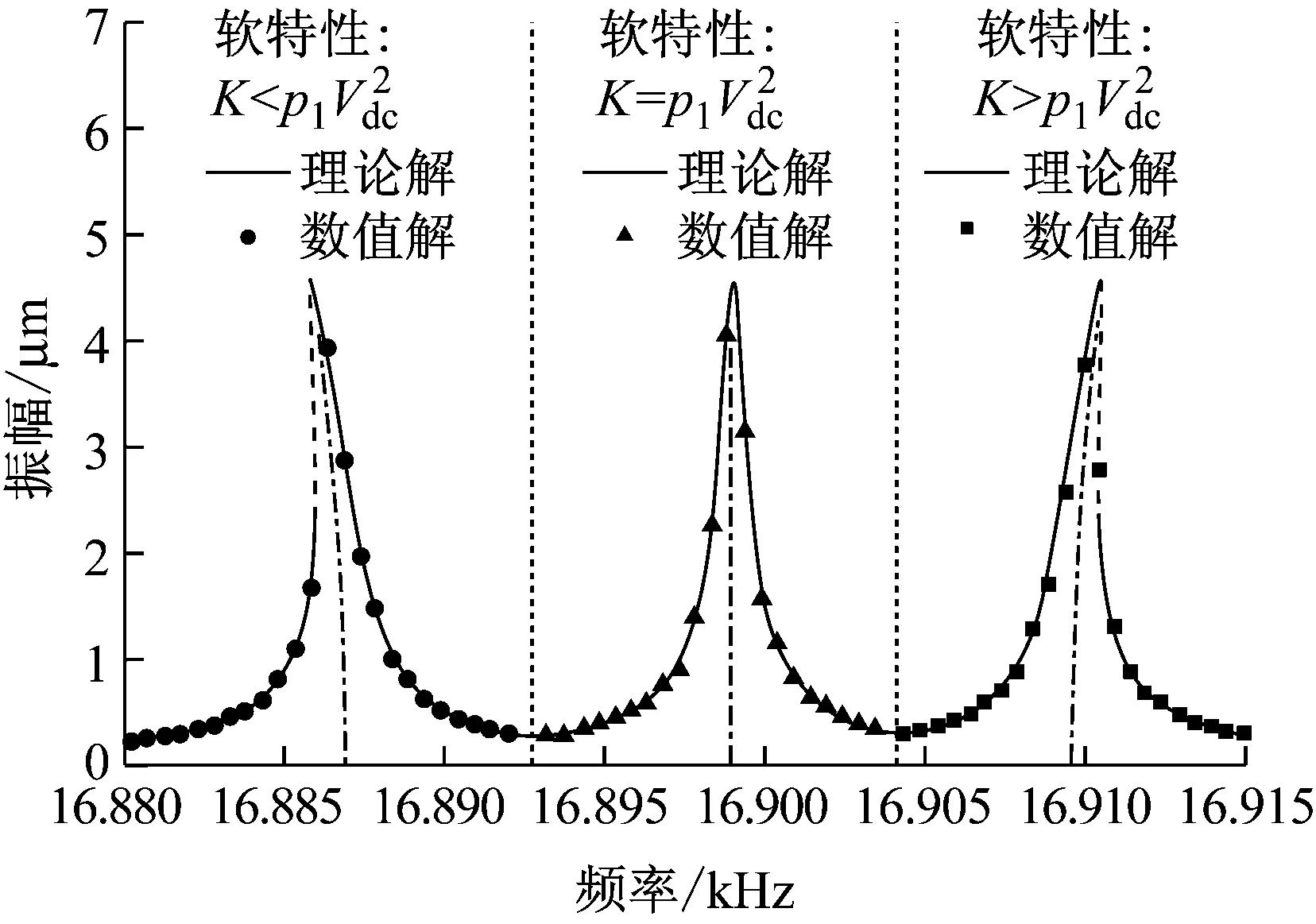
下面同样采用一组参数进行验证,以图9为例,假设微梳齿谐振器的设计工作频率为16.9 kHz,可以得到软硬特性过渡的参数情况。对该组参数进行理论及与数值仿真分析,结果如图10所示,从而验证了理论公式的正确性。
本节通过讨论MEMS梳齿谐振器的软硬特性过渡状态,得到结论:系统最优设计电压随着初始间距的增大而逐渐增大;设计频率随着初始间距的增大而逐渐减小;与无限大平行板模型相比,边缘效应模型到达软硬特性过渡的临界电压值偏小,对应的等效固有频率偏大。

图10 线性过渡下的幅频响应曲线
4 结 论
本文借助理论分析和数值模拟方法讨论了边缘效应下梳齿谐振器的静动力学特性,结论如下:
(1) 边缘效应下,梳齿微谐振器的静电激励力明显增强,振幅明显增大。边缘效应模型与无限大平行板模型相比,系统的动态可行域偏小,稳定性偏低,发生吸合失稳的概率偏高。
(2) 系统的谐振频率随着梳齿初始间距的增大而逐渐增大,随着电压的增大而逐渐减小。边缘效应下梳齿谐振器的谐振频率的偏小,共振频带发生偏移。
(3) 梳齿微谐振器的软化行为是由静电力引起的。边缘效应增强了MEMS梳齿谐振器的静电驱动力,导致幅频特性曲线的软化行为得到增强。
(4) 幅频曲线的线性过渡现象可以增强MEMS系统的线性度,提高谐振器的工作性能。线性过渡下系统的最优设计电压会随着初始间距的增大而逐渐增大,对应固有频率随着初始间距的增大而逐渐减小;与无限大平行板模型相比,边缘效应模型到达软硬特性过渡的临界电压值偏小,对应的等效固有频率偏大。
