振荡流下柔性立管涡激振动时域响应研究

袁昱超， 薛鸿祥， 唐文勇

(1. 上海交通大学 海洋工程国家重点实验室， 上海 200240;2. 上海交通大学 高新船舶与深海开发装备协同创新中心， 上海 200240)

柔性立管在真实海洋环境下的涡激振动(Vortex-Induced Vibration，VIV)是一个复杂的流固耦合问题。当海流流经立管时，立管周围会产生周期性的漩涡脱落，引发按照Strouhal频率振荡变化的激励力反馈。对于柔性立管，激励力作用下的运动响应又会干扰周围流场分布及相应的流体力，流体与立管相互耦合作用下激励力的频率将偏离预期的Strouhal频率，涡激振动幅值将会明显增大，称为“锁定”，“锁定”现象的存在易使立管造成严重的疲劳损伤甚至结构失效。因此，加深对涡激振动机理的认识以及寻求行之有效的预报方法迫在眉睫。

对于细长结构物涡激振动的预报，现有数值模型总体上可分为频域和时域两类方法。基于半经验模型的频域预报工具已发展得较为成熟，如SHEAR7[1]和VIVANA[2]，但频率方法无法考虑非定常流工况以及浮体、海床等复杂边界条件效应，相较之下时域预报方法考虑得更为全面且适用于更广泛的对象及工况。时域方法根据其依托的核心算法可分为两类：尾流振子法和半经验模型法。尾流振子法采用Van der Pol振子模型描述流场，Chang等[3]基于此类方法预报了某立管在由于顶端平台垂荡运动产生的非均匀流下的涡激振动，但与众多尾流振子模型相似，如何找到一套控制参数使得数值模型预报结果普遍满足不同试验实测数据仍然存在一定的难度。因此，半经验模型法近年来受到了国内外学者及研究机构越来越多的关注。Sidarta等[4]，Ma等[5]和Xue等[6]基于不同受迫振动试验数据相继开发了一些涡激振动时域预报模型，并结合定常流下模型试验结果验证了各自方法的有效性。Liao[7]定义了约化阻尼及波传播系数并提出了一套预报非定常流下细长结构物涡激振动的数值方法，但尚未得到相关试验验证。Resvanis[8]推荐了可用于确定非定常流下涡激振动是否与定常流下相似的无因次参数。Thorsen等[9]也开发了一套时域半经验模型方法，可用以预报立管定常流及振荡流下涡激振动响应。

如何获取流体力系数是半经验模型方法关注的核心。从原理上来讲，流体力系数独立于时间域，且对于非定常流而言，在每一个极小的时间间隔内均可认为满足定常流条件，因此不难猜测适用于定常流工况的流体力系数库应同样适用于非定常流条件。本文提出了一套可供选择的涡激振动半经验模型方法，可用于预报振荡流下柔性立管的结构响应，所有相关水动力系数均来自于受迫振动试验数据[10]。上述方法将现有流体力系数库运用于非定常流工况，采用了全新的锁定区间及锁定准则。本文结构安排如下，第一章对本文推荐数值模型的原理及方法进行了描述，第二章选取文献[11]中公布的振荡流下柔性立管涡激振动模型试验作为对比，论证了本文推荐方法的有效性，第三章从涡激振动发生机理层面剖析了振荡流下结构响应呈现诸多有别于定常流工况特征的原因，第四章对振荡流及均匀流下结构动力响应进行了对比，第五章对全文进行总结并给出通过本文研究得到的若干结论。

1 涡激振动响应分析模型

深海柔性立管通常具有较大的细长比，因此立管模型可认为是服从Euler-Bernoulli梁模型假定的抗弯弹性结构，其横流方向的运动控制微分方程由式(1)表示，本文选取Cartesian坐标系，x轴为顺应流速方向，y轴为与流速垂直的横流向，z轴为竖直向上方向

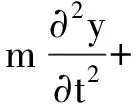
(1)

式中：m为立管单位长度质量；c为阻尼系数，包括结构阻尼及水动力阻尼成分；E为弹性模量；I为惯性矩；T为有效张力；A*为相对于立管直径D的无因次幅值；fr为无因次频率，fr=f·D/V；f为响应频率，Fy为流体力。

流体力Fy由与立管速度同相位的激励力FV和与立管加速度同相位的惯性力FM两部分组成。上述两个流体力成分均由立管响应频率、振动幅值以及遭遇流速共同决定。本文假定作用于立管单元的激励力在一个周期内服从正弦规律变化，流体力可表示为式(2)所示的形式

(2)

式中：CV为激励力系数；ω为响应频率对应的圆频率；ρf为流体密度；Ca为附加质量系数，本文参照势流理论取1.0；V为时变流速。

1.1 激励力模型

Gopalkrishnan开展了一系列圆柱体单自由度受迫振动试验研究，获取的激励力系数云图如图1所示。图中粗实线标注出激励力系数为零的边界，此边界是判定涡激振动是否发生的关键指标。本文将三维系数云图简化为无因次频率为0.17处对应的二维系数曲线，由图1可知，无因次频率为0.17时，激励力系数达到最大值。因此，实际用到的激励力系数为仅随无因次幅值变化的函数，如图2所示。当无因次幅值大于0.9D，激励力系数小于零时，或无因次频率超出系数云图范围时，均认为此时激励力将转化为水动力阻尼，转化方法如1.2节所述。另外，试验中对应的Strouhal数为0.193。

1.2 阻尼模型

本文阻尼模型由结构阻尼和水动力阻尼两部分构成。结构阻尼cs通常表示为

cs=2mωξ

(3)

式中：ξ为结构阻尼比。

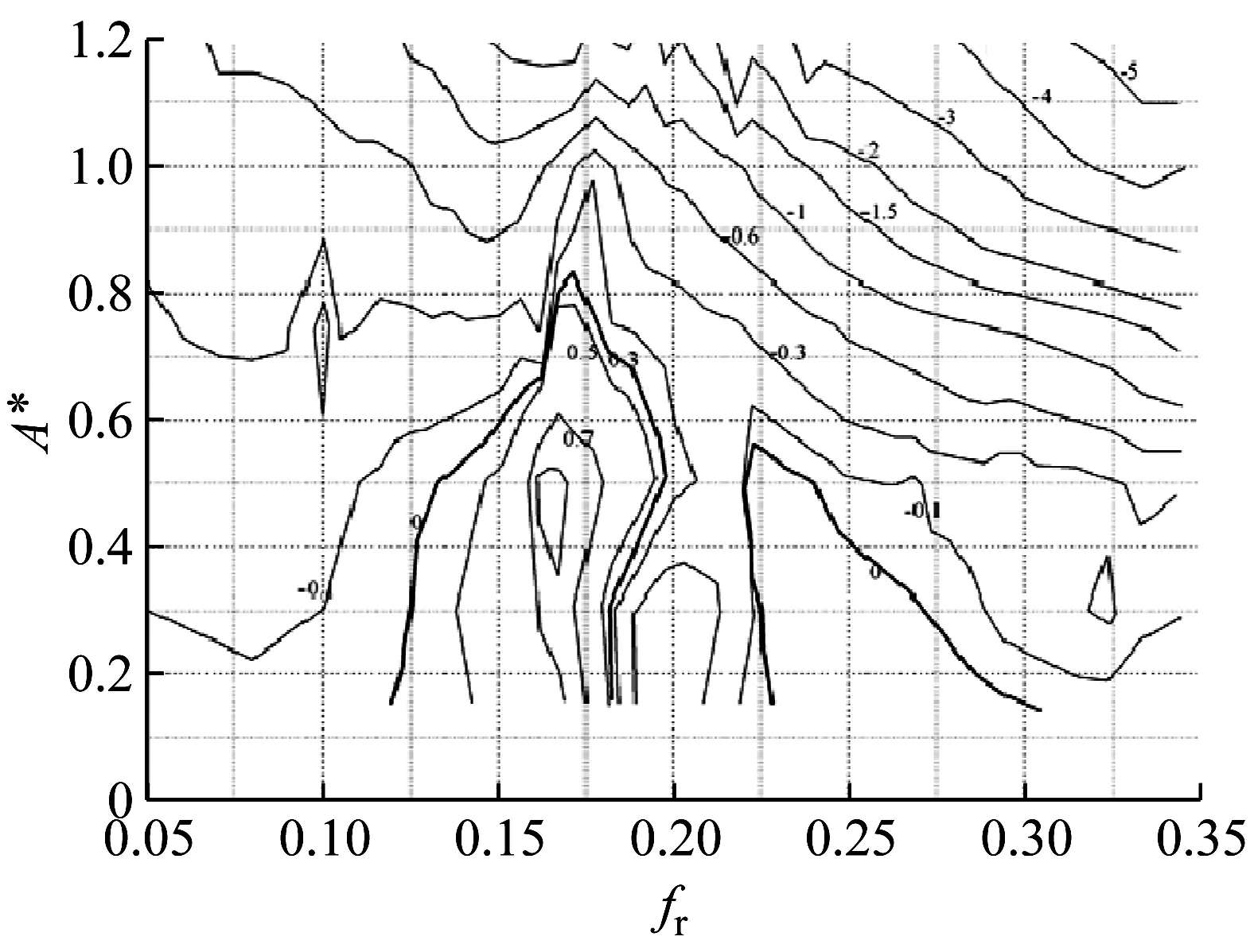
图1 激励力系数云图

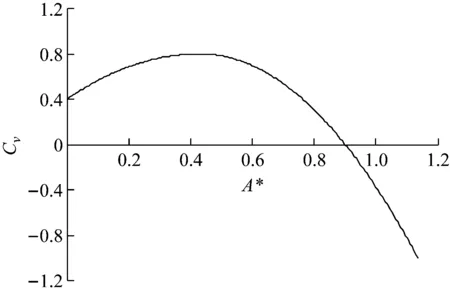
图2 激励力系数曲线(fr=0.17)

当激励力系数大于零时，激励力与立管速度同向，整个系统内能量由流体传入立管，而当激励力系数小于零时，水动力阻尼力作用于立管，能量也将由立管传回流体。参考涡激振动频域方法中的处理手段，本文假定流体传入立管的等效能量在一个振动周期内传回流体，根据能量守恒原理，水动力阻尼系数可通过式(4)计算得到

(4)

如果无因次频率超出图1所示试验数据范围，本文采用由Venugopal[12]针对涡激振动提出的经验阻尼模型模拟水动力阻尼，该经验阻尼模型分为低频区及高频区两个区域低频区水动力阻尼由式(5)表示

cf=ClfρfV2/ω

(5)

其中，Clf为经验系数，本文推荐取0.2。

高频区水动力阻尼由式(6)表示

cf=ChfρfDV+csw

(6)

式中：Chf为经验系数，本文取0.18；csw为静水阻尼，可由式(8)计算所得

(7)

式中：ν为流体运动黏度系数；Csw为经验系数，取0.25。

1.3 锁定判定准则

立管涡激振动的响应幅值和频率是计算流体力最为关键的输入参数，因此在每一分析步内，需要提取节点位移(u)、节点速度(v)以及当前时刻(t)以确定立管每一个单元的实时响应幅值及频率。立管振动幅值Aosc和频率fosc可通过式(8)得到

Aosc=|ub-ua|/2

fosc=1/[2×(tb-ta)]

(8)

其中，ua,ub,ta,tb为相邻两个v= 0 的时刻点a和b对应的位移和时刻。

依据Zheng[13]在MIT拖曳水池开展的两自由度刚性圆柱体受迫振荡试验研究成果，本文选取的无因次频率锁定区间为[0.125,0.25]，该锁定区间需要根据真实环境与试验环境的差异采用式(9)进行Strouhal数修正。若无因次振动频率落在锁定区间内，锁定发生，立管单元将锁定到无因次频率0.17上，视为涡激振动主导频率，用于计算激励力。根据激励力系数云图(图1)，涡激振动激励中心对应的无因次频率约为0.17，选取0.17作为无因次主导频率可保证激励力系数取到峰值，以得到略微保守的预报结果。在下文的模型试验验证中，基于本文推荐方法的预报结果与试验观测吻合较好，因此可认为本文采用的略微保守的激励力能够得到较为合理的预报结果。若无因次振动频率在锁定区间外，认为主导频率等于振动频率，进而根据图1得到小于零的激励力系数后通过式(4)得到水动力阻尼系数。若无因次振动频率超出系数云图范围，采用1.2节中介绍的经验阻尼模型获取水动力阻尼系数。

(9)

为更加方便直观地描述本文推荐方法，图3给出了涡激振动时域分析流程图。

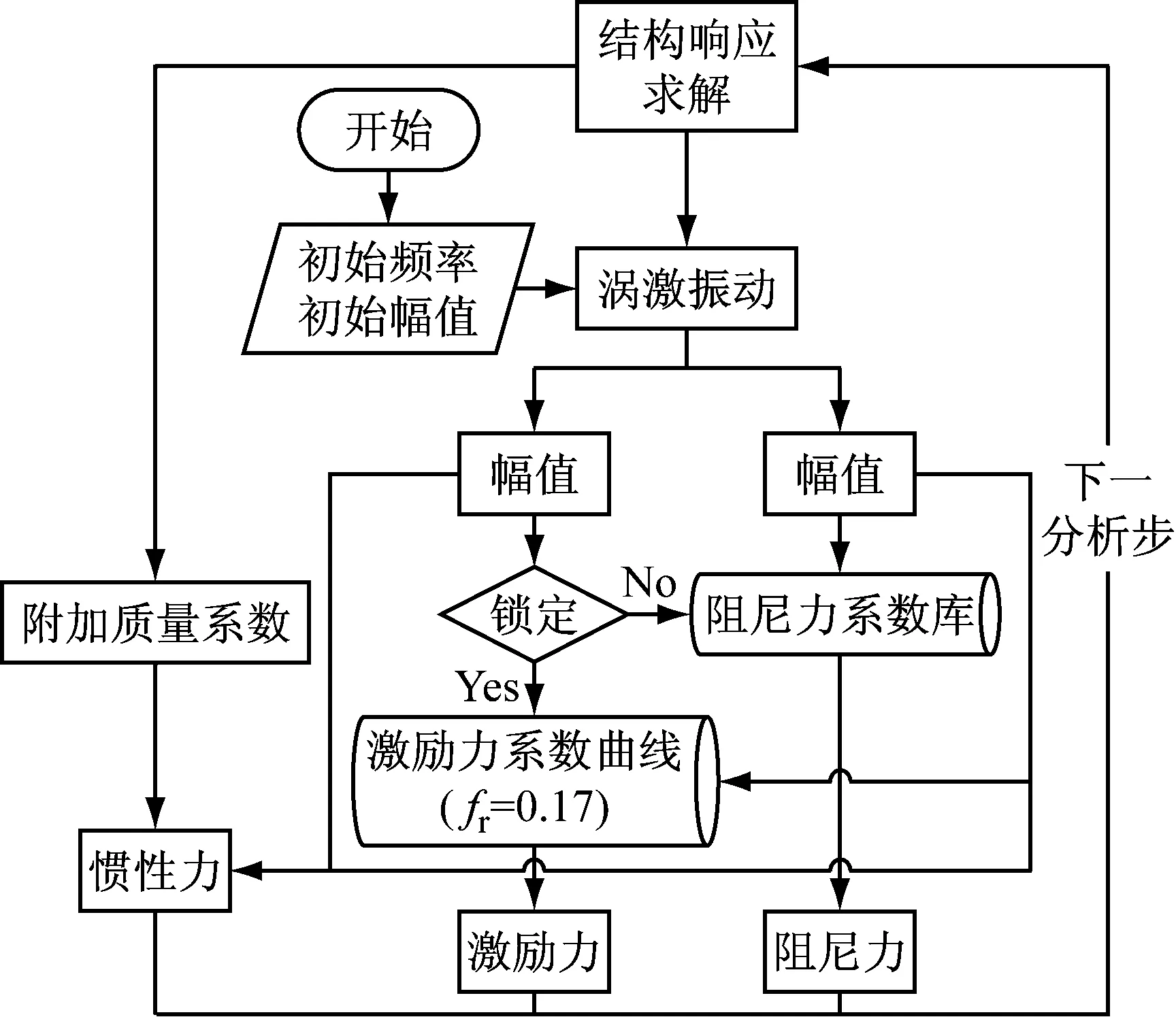
图3 涡激振动时域分析流程图

2 振荡流工况模型试验验证

当流体随时间呈现周期性振荡，其运动方程可表示为式(10)

(10)

式中：Am为最大振荡幅值，Vm为最大振荡流速,T为振荡周期。另一个常被用于描述某一特定振荡流的关键参数为Keulegan-Carpenter (KC) 数，表示形式如式(11)所示

(11)

本文选取上海交通大学海洋工程国家重点实验室开展的振荡流下柔性立管涡激振动系列试验[14]作为模拟对象，通过对模拟结果与试验数据进行对比分析，评估本文方法的预报精度。整套试验装置安装在拖车底部，试验装置主要由两条水平轨道构成，水平轨道上的伺服电机带动模型以设定的振幅Am和振荡周期T在静水中进行水平简谐振荡，从而实现立管模型遭遇等效振荡来流作用。图4为该试验装置简化示意图，立管模型主要参数如表1所示。定常流下涡激振动响应研究中，约化速度被视为最为重要的参数之一，在振荡流工况下，Fu等将最大约化速度定义为式(12)形式

(12)

式中：f1为立管模型静水中一阶固有频率(假定附加质量系数为1.0)。

Fu等根据模型试验观测结果研究振荡流下立管涡激振动响应时发现，在KC数较大和较小两种情况下结构会分别表现出差异明显的响应特性。文献[11]分别以178和31为例给出较为完整的试验结果并展开讨论。因此，本文同样选取178和31两种KC数(分别代表大KC数和小KC数工况)下对应的试验数据与预报结果进行直接对比以验证推荐的涡激振动时域数值模型对于预报不同KC数振荡流工况的有效性。目前关于涡激振动的研究主要关注漩涡脱落较为规律的亚临界流动区域，受迫振荡激励力系数库也是在雷诺数介于亚临界流动区域内获取，而最大约化速度为7.9的工况可能已超出亚临界流动区域，受迫振荡试验所得激励力系数库已不再适用，因此本文研究工作暂不涉及最大约化速度为7.9的工况。对于此类工况的数值模拟研究有待今后继续开展相关试验加深对高雷诺数下涡激振动机理的认识。

本文在与文献[11]对应的大、小KC数下各选取两个工况，共四个工况(见表2)，基于推荐方法进行数值模拟以评估不同KC数及最大约化速度组合下涡激振动响应及预报精度。上述试验工况均处于亚临界流动区域，对应的Strouhal数取0.2。另外，本文通过连续小波变换获取振荡流下涡激振动应变时-频响应云图，母小波参照文献[11]选取Morlet小波。

图5 ～图8为四个计算工况预报结果与试验数据对比情况，第一列为基于本文数值模型的预报结果，第二列为文献[11]中截取的对应试验数据；第一行为立管模型中点处涡激振动位移时历曲线，第二行为涡激振动应变时-频响应图谱(横坐标表示时间，纵坐标表示频率，颜色深浅表示振动能量集中程度)，立管模型前两阶实时固有频率及对应来流完整振荡周期的时间间隔也在试验数据中有所标注。

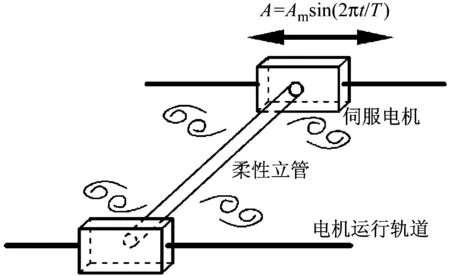
图4 试验装置示意图

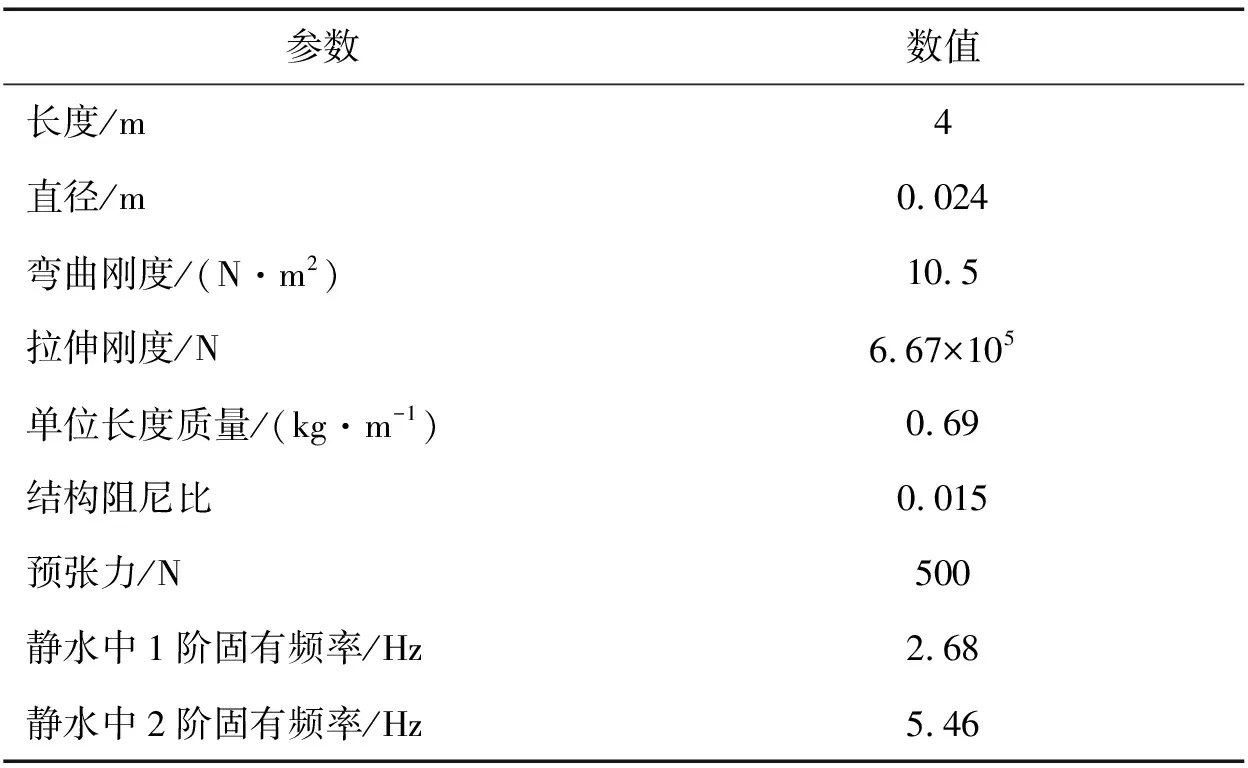
参数数值长度/m4直径/m0.024弯曲刚度/(N·m2)10.5拉伸刚度/N6.67×105单位长度质量/(kg·m-1)0.69结构阻尼比0.015预张力/N500静水中1阶固有频率/Hz2.68静水中2阶固有频率/Hz5.46

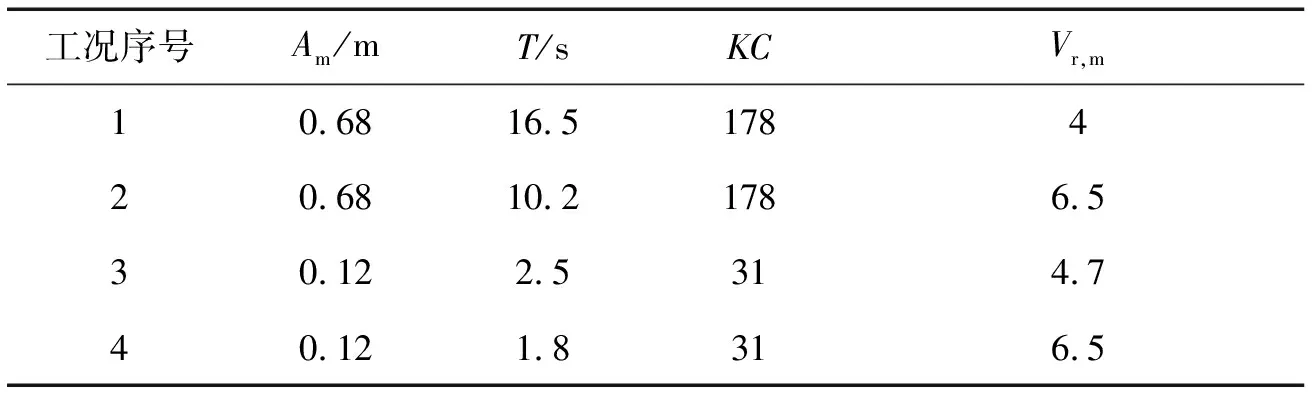
表2 对比试验工况列表

2.1 大KC数工况

大KC数表征振荡幅值较大，最大约化速度相当时，意味着该振荡流具有较长周期。图5和图6给出了工况1及工况2的涡激振动响应。预报结果呈现出一些区别于定常流条件的结构响应形式，试验观测中也同样发现了如下文所述典型特征。

(1) 间歇涡激振动

定常流与振荡流最直观的不同点在于后者的流速随时间变化，因此不难猜测振荡流下的涡激振动响应可能具有时变特征。根据预报的位移时历曲线可以发现，涡激振动的发生展现出间歇性，在一个振荡周期内，振动幅值在相当长的时间间隔内接近于零。这种间歇涡激振动在相对较长的时间间隔内仍然保持明显的周期性及规律性。试验观测信号同样出现了间歇性涡激振动现象。

(2) 振幅调制

预报及试验结果中，另一个显而易见的现象是，与间歇涡激振动对应，振动幅值同样随时间变化，即振幅调制。振动幅值随流速的增大或减小呈现出相似的变化趋势。在一个振荡周期内，由于分别存在两个时间片段对应流速的增大及减小，响应幅值与之对应地按 “山峰”状发生两次调制过程。无论是调制的过程还是响应幅值的范围和极值，预报结果与试验数据均高度一致。

(3) 迟滞现象

振荡流可认为是连续的且严格对称的加速及减速过程，加速段对应流速由0增加至最大流速的时间间隔，而减速段对应流速由最大流速减小至0的时间间隔。如图6中的试验数据所示，(A/D)acc和(A/D)dec分别表示加速及减速过程中流速相同的两个时刻对应的振动幅值，很显然(A/D)acc和(A/D)dec并不相等，前者明显小于后者，这种响应形式在文献[11]中被称为“迟滞”现象。在工况1及工况2的预报结果中，同样可以发现迟滞现象的存在。

(4) 频率转换

立管应变时-频响应图谱中，涡激振动响应频率呈现与振幅调制相似的时变特点。结构振动频率大致上与流速成正比，因此，在一个振荡周期内存在两次明显的频率转换过程。预报得到的工况1及工况2时-频响应形式及转换范围均表现出与对应试验结果吻合的规律性，相同时间间隔内，位移时历曲线出现的半波数也基本相等，能量集中区域大致对应立管模型一阶固有频率。

(5) 高频谐振

预报及试验信号得到的应变时-频响应图谱中，均在不同程度上发现了高频谐振(大约三倍于涡激振动主导频率)成分。该高频谐振成分已在大多数柔性立管涡激振动模型试验中被证实存在，目前普遍认为是由于被称为“2T”的漩涡脱落形式产生的。而本文采用的激励力系数库是基于刚性圆柱体受迫振荡试验数据，对于这一高频区域的现有信息暂不完整，因此预报及试验结果未必完全吻合，本文主要关注基础激发频率下的涡激振动响应。

(6) 涡激振动发展过程

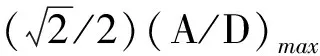
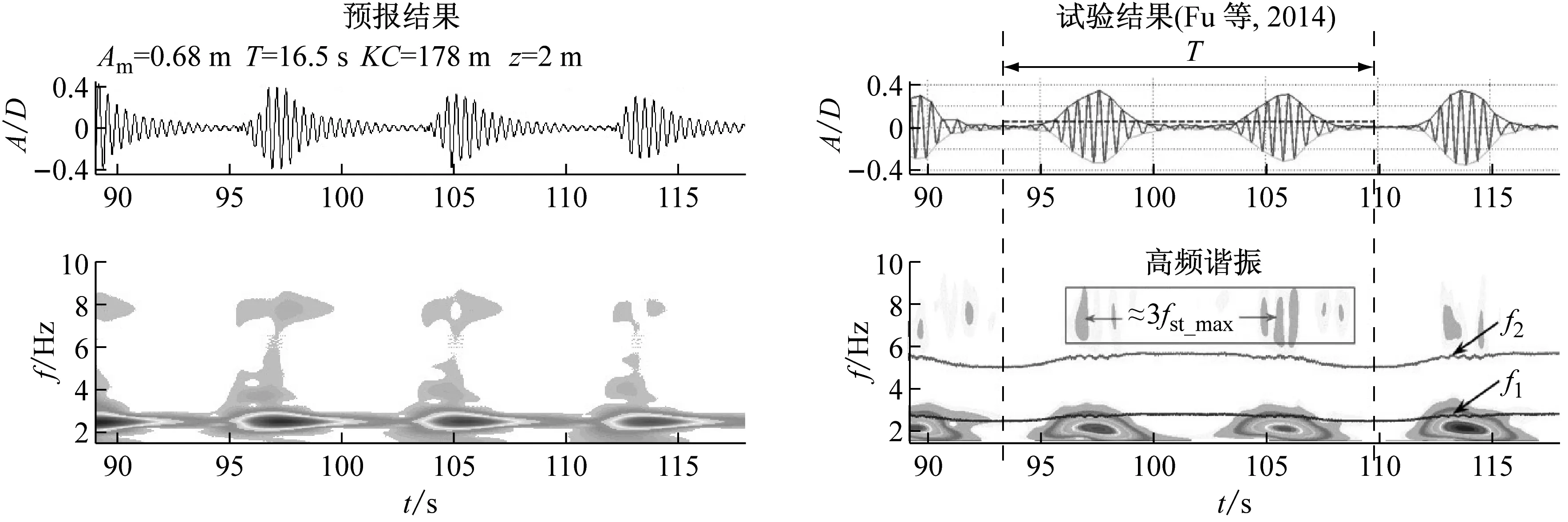
图5 工况1(Vr,m=4, KC=178)下z=2 m处涡激振动响应

2.2 小KC数工况

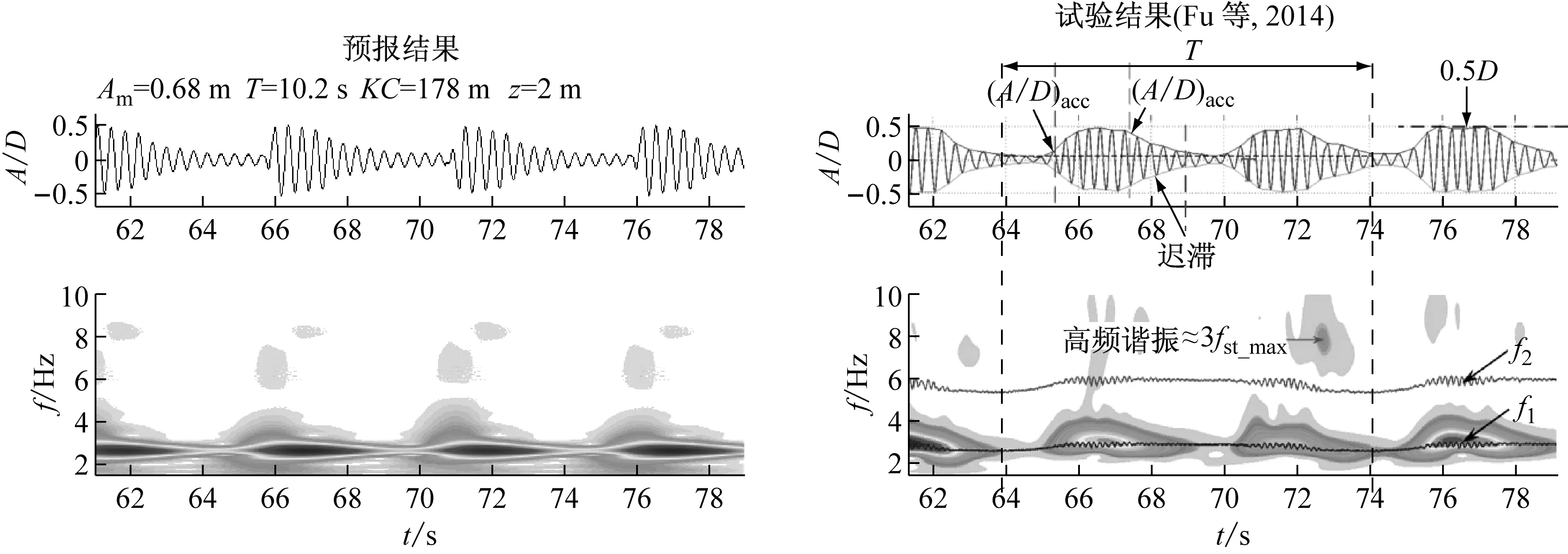
图6 工况2(Vr,m=6.5, KC=178)下z=2 m处涡激振动响应

对于小KC数工况，流动的振荡幅值较小，最大约化速度相当时，振荡周期普遍较小，即流动特性将随着时间剧烈变化。工况3及工况4的涡激振动响应分别如图7及图8所示。虽然同为振荡流工况，小KC数下的涡激振动响应表现出一些与大KC数下明显不同的特征。

(1) 振幅调制

小KC数下的响应位移时历曲线中同样可以发现振幅调制现象，但此时的调制过程与大KC数下有所不同，幅值在时间域上的波动无明显的规律性，更像是因为结构不稳定振动产生而非由流速周期性的变化特征导致。工况3的预报结果给出了与试验类似的无规律时历曲线且最大幅值与试验值大致相等。对于工况4，预报所得响应幅值相对恒定且时历曲线与均匀流条件下的正弦振型具有一定相似性，试验结果亦然。

(2) 频率转换

对于工况3，图7中的试验结果显示仍然存在一定的频率转换现象，而预报得到的应变时-频响应图谱中响应频率随时间变化保持恒定，虽然数值模拟与试验观测存在一定差异，但位移时历曲线中相同时间间隔内出现的半波数仍然较为一致。对于工况4，图8中的预报及试验结果均表明涡激振动主导频率在时间域上保持连续，且对应数值基本相等。两计算工况下，能量集中区域仍大致对应立管模型一阶固有频率。

(3) 高频谐振

在小KC数下，约等于被激发基础频率三倍的高频谐振成分同样出现在预报及试验结果中。目前被广泛接受的可准确预报这一高频成分的数值模拟手段仍然较为缺乏，本文目前仅证明了这一高频谐振现象的存在，至于如何加深对这一高频成分的认识以及在定常流甚至非定常流下有效地进行预报，仍有更多更深入的研究工作需要进一步开展。

2.3 讨论与总结

经上述分析证实，振荡来流会导致柔性立管发生涡激振动，但在不同KC数下，涡激振动响应呈现出不同的特征。当KC数较大时，会观察到一些明显与定常流条件下不同的响应特性，如间歇涡激振动、振幅调制、迟滞现象、频率转换及高频谐振，位移时历曲线也呈现出完整的包括建立、锁定、衰减三个阶段的涡激振动发展过程。而当KC数较小时，涡激振动响应相对不稳定，虽然也能观察到振幅调制及频率转换现象，但周期性及规律性并不足够明显，响应幅值在时间域上基本保持恒定且响应频率保持连续，以上特性与均匀流下涡激振动响应形式较为接近。

图7 工况3(Vr,m=4.7, KC=31)下z=2 m处涡激振动响应

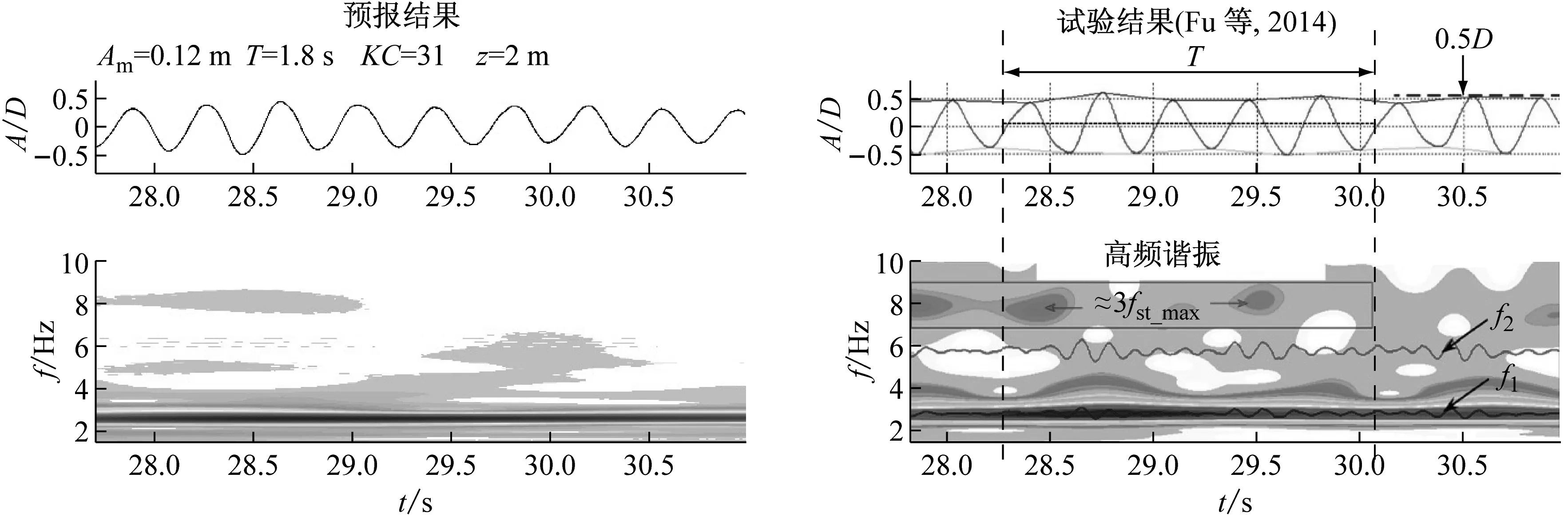
图8 工况4(Vr,m=6.5, KC=31)下z=2 m处涡激振动响应

本文选取的四个振荡流工况中，最大约化速度为6.5，对应的最大瞬时流速约为0.42 m/s，无因次频率0.17对应的涡激振动主导频率约为2.97 Hz。而根据文献[11]可知，立管模型的二阶固有频率为5.46 Hz，即最大瞬时流速仍不足以激发二阶振动模态。因此，预报结果与对应的试验观测中均未出现二阶振动模态被激发的现象。总的来说，计算的四个工况下，无论振幅调制、频率转换的形式及波动范围，还是不同KC数下各自的响应特性，预报结果均呈现出与试验数据较好的一致性及相似的规律性。对于某一真实海况，海流流动通常具有较大的振荡幅值及较长的运动周期，这意味着对应较大的KC数及较小的最大约化速度，因此深海柔性立管在真实海洋环境下的涡激振动响应更接近于工况1及工况2反映的情况，而这两个工况下的数值模拟及试验观测高度吻合，因此可以认为本文推荐方法可以较为有效地预报振荡流下柔性立管涡激振动响应。

3 涡激振动机理分析

本章将针对上文数值模拟及试验验证中反映出的柔性立管振荡流下涡激振动有别于定常流条件的响应特性，从涡激振荡发生机理层面详细分析讨论，探求产生上述现象的原因。

圆柱体自激振动试验研究表明[15]，当名义约化速度Vr介于[4,8]之间，结构将发生明显的涡激振动，且无因次响应位移幅值A/D将在Vr=6附近达到极大值，这也正是本文将无因次频率激励区间及主导频率取[0.125,0.25]和0.17的依据。当Vr在上述激励区内，激励力作用于立管，加剧结构振动，而当Vr位于上述激励区外，即Vr<4或Vr>8,激励力将转化为水动力阻尼，起到减弱结构振动的作用。本文涉及的计算工况下，主要被激发的模态均为一阶，因此，激励区及阻尼区可按照图9及图10中的标记方法进行表示。

3.1 大KC数工况

对于大KC数工况，流动的振荡幅值通常较大，足够漩涡像定常流条件下脱落完全。振荡流(KC=178)及相关临界流速时历曲线如图9所示。在每半个振荡周期内，立管将先由阻尼区进入激励区，再由激励区回到阻尼区。观察到的间歇涡激振动现象正是发生在立管位于激励区时，且立管在阻尼区及激励区之间的来回转换过程也解释了由建立、锁定、衰减三个阶段组成的涡激振动循环发展过程及振幅调制现象。Vr,m=6.5与Vr,m=4相比，半周期内流速处于激励区时间比例更大，因此锁定阶段占半周期的份额也相应更大。而流速的时变效应也势必导致涡激振动主导频率随时间变化，从而反映为响应频率存在转换过程。

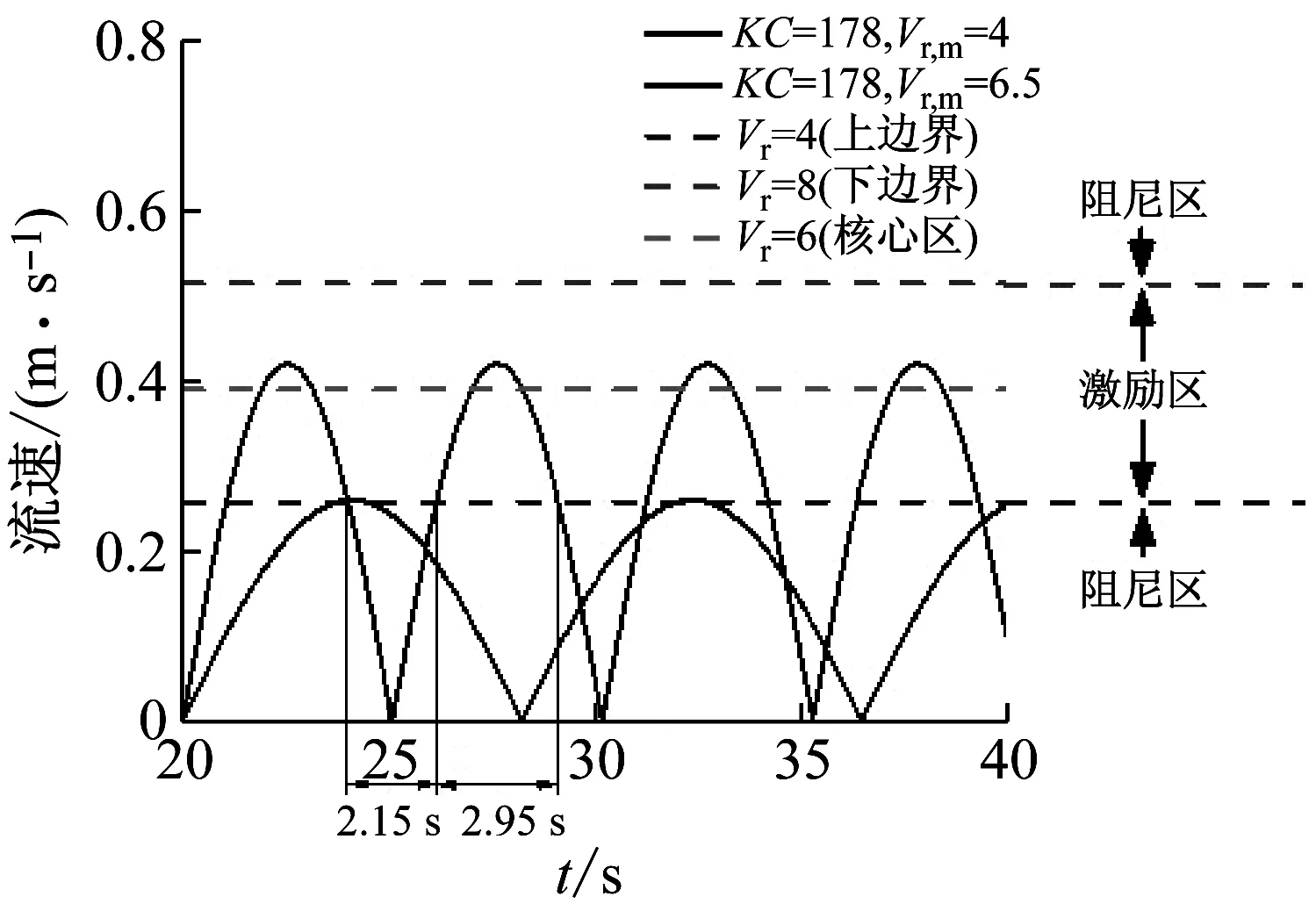
图9 振荡流及均匀流下流速时历曲线(KC=178)

当结构物受到某一时变载荷作用，通常需要一定的时间才能给出相应的结构响应，即响应与载荷之间存在着一定的延迟效应，锁定发生时，激励力与流速平方成正比，流动加速阶段激励力逐渐增大，结构振动趋于增强，但响应幅值的增大稍慢，而减速阶段，结构振动趋于减弱，响应幅值的减小同样较激励力的减小存在延迟，两方面因素共同作用下导致(A/D)acc小于(A/D)dec，这也正是迟滞现象产生的原因。事实上，不同KC数振荡流工况下响应与时变载荷间的延迟效应一直存在。在大KC数工况下，来流振荡周期较长，周期性的动力响应较为稳定，响应与载荷之间存在的延迟效应以迟滞现象的形式显现得较为清晰。小KC数工况下，虽然载荷与响应间的延迟效应同样存在，但由于来流振荡周期较短，流速变化较快，结构本身的动力响应不再具有周期性，迟滞现象也很难在不稳定的位移时历曲线中捕捉到。

需要指出的是，大KC数工况下结构动力响应展现出的振幅调制现象应与定常流条件下柔性立管涡激振动的拍频现象予以区分。戚兴等[16-18]在对圆柱体涡激振动开展数值模拟研究时发现，定常流条件下立管涡激振动中存在拍频现象。拍频可以理解为立管由非锁定向完全单一频率锁定过渡的一种中间状态。当立管达到完全锁定状态时，拍频现象不再出现。本文锁定判定准则中认为仅存在非锁定和完全锁定两种状态，不考虑“拍频”这一过渡状态，一旦无因次响应频率落在锁定区间内，立管结构完全锁定，激励力系数唯一确定，流体力载荷仅存在主导频率这一个频率成分。因此，大KC数振荡流工况下捕捉到的振幅调制并非拍频现象引起，而是由于来流流速随时间变化所致。

3.2 小KC数工况

当流动振荡幅值较小，即对应小KC数，立管下流向边界层分离将不明显。立管仍然处于上半周期振荡流动造成的扰动流场中时，流动已在下半周期出现转向。这种情况下流体的黏性效应将减弱，也就是水动力阻尼对立管振动的阻碍作用将相较大KC数条件下不明显。因此，小KC数振荡流下立管涡激振动响应与均匀流条件下相似。图10给出振荡流(KC=31)及相关临界流速时历曲线，两计算工况中，较大的半周期也仅有1.25 s。对于本文提出的数值模型，即使进入阻尼区，振动幅值的衰减仍需要一定的时间，然而阻尼作用的绝对时间太短，以至于还未充分减弱振动，激励力又重新占据主导。因此小KC数工况预报所得响应幅值基本保持恒定，即使如此，适用于定常流条件的阻尼模型仍然高估了振荡流下的实际阻尼，所以预报的最大振幅普遍略小于试验观测值。另外，由于处在激励区及阻尼区的绝对时间均极短，激励力及水动力阻尼频繁变化及转换，结构响应也更容易出现不稳定现象，同样反映为响应振幅调制及频率转换。

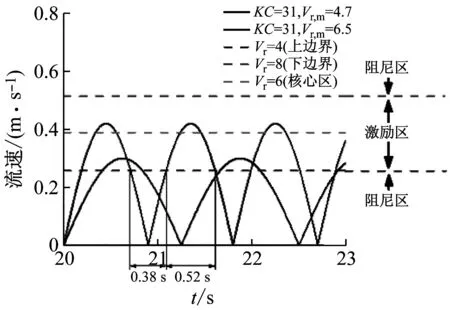
图10 振荡流及均匀流下流速时历曲线(KC=31)

4 振荡流与均匀流下立管动力响应对比

本文推荐方法除适用于柔性立管振荡流下涡激振动预报外，还可用于定常流条件下结构动力响应模拟。本章基于第二章振荡流工况预报结果模拟同一立管模型可与之对比的相关均匀流工况，并参照第三章的分析方法从涡激振动机理层面对振荡流及均匀流下结构动力响应对比结果予以解释。

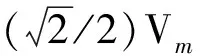
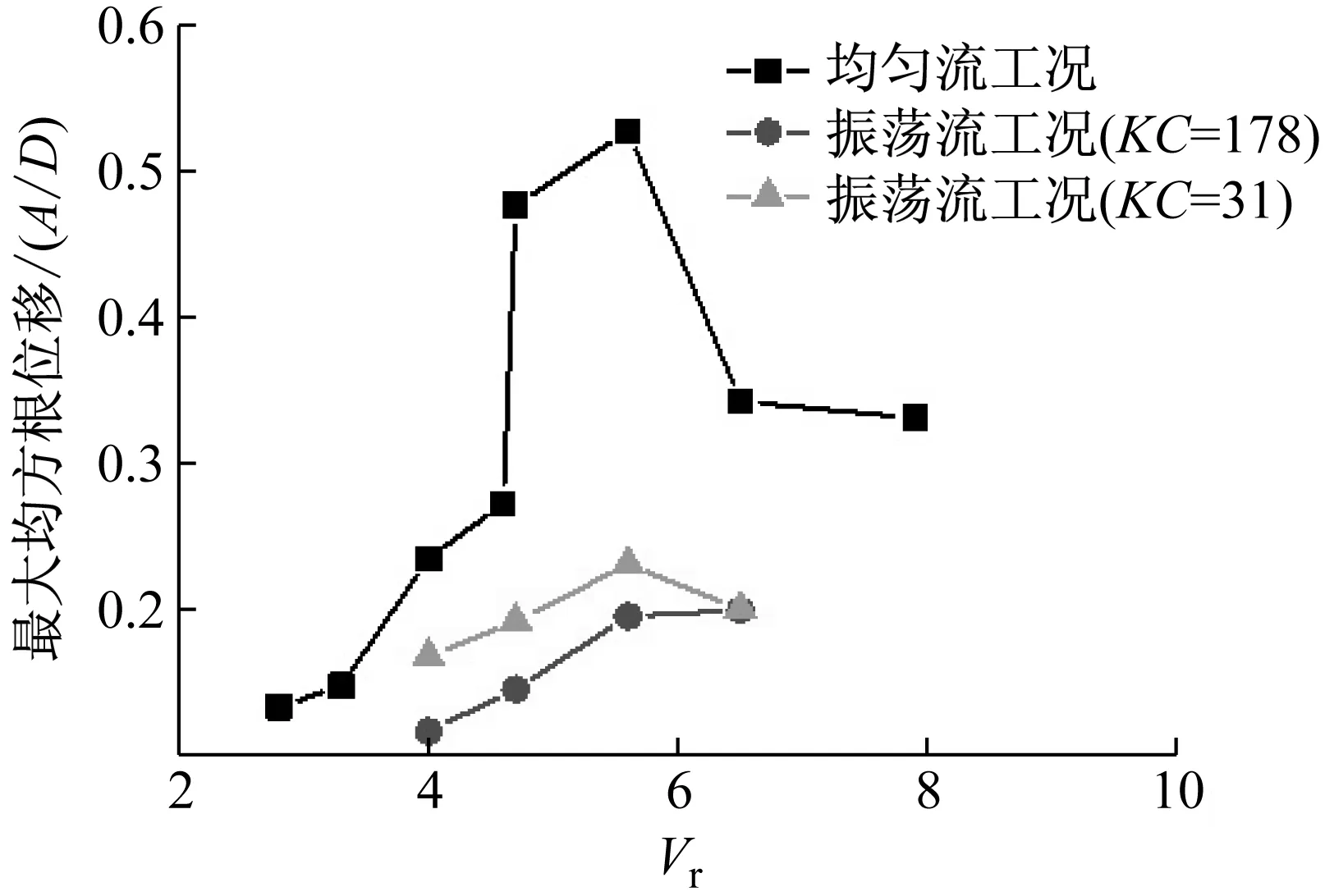
图11 振荡流与均匀流下最大RMS响应位移对比

对于均匀流工况，响应位移(A/D)max的峰值出现在Vr=5.6工况，当Vr<5.6时，(A/D)max随着Vr的增大而增大，当Vr>5.6时，(A/D)max随着Vr的增大而减小，上述规律与诸多圆柱体自激振动试验结果[15]相吻合。对于振荡流工况，KC数相同时，同样表现出Vr,m=6附近 (A/D)max达到极值，Vr,m向两侧发散时，(A/D)max逐渐减小；而当Vr,m相同时，小KC数(KC=31)下(A/D)max均大于大KC数(KC=178)下的对应值，且随着Vr,m的增大，相同两个KC数下(A/D)max之间的差距将被缩小。而对比振荡流及均匀流工况可以发现，振荡流条件下的(A/D)max普遍小于对应最大流速及均方根流速的均匀流工况。

由于激励力系数最大值大约出现在Vr=6附近，本文暂且将其称为激励核心区，因此均匀流工况下(A/D)max在Vr最接近6的5.6处达到极值。同样的原因也适用于KC数相同而Vr,m不同的振荡流工况，对于Vr,m=4及Vr,m=4.7，一个周期内大部分的时间位于阻尼区，相较之下，Vr,m=5.6及Vr,m=6.5处在激励区当中的时间更长，且有相当长一段时间瞬时约化速度在激励核心区，激励力对结构振动增强效应明显，因此 (A/D)max也相对更大。而当Vr,m相同时，易知存在的关系，因此随着Vr,m的增大，相同两个KC数下，振荡流振荡周期之间的差距将逐渐缩小，即两个振荡流工况趋向于相同，这也解释了为何(A/D)max之间的差距也相应缩小。

另外，当柔性立管在均匀流下发生涡激振动时，本文假定立管始终处于锁定状态，只受激励力、惯性力及结构阻尼作用。而对于振荡流工况，由于存在水动力阻尼对结构振动的减弱效应，(A/D)max小于对应的均匀流工况，又因为随着KC数的减小，流体黏性作用减弱，即水动力阻尼越发不明显，因此相同Vr,m条件时，小KC数下的(A/D)max大于大KC数工况的对应值。而对于Vr=2.8和Vr=3.3这两个对应Vr,m=4和Vr,m=4.7均方根流速的均匀流工况，由于已不在激励区，稳定的涡激振动并不明显，(A/D)max同大KC数下的间歇的涡激振动对应值相近，但与Vr,m=4和Vr,m=4.7对应的小KC数振荡流工况相比，后者涡激振动与均匀流条件相似，且相当长时间内位于激励区内，激励力对结构振动的增强作用明显，因此(A/D)max大于Vr=2.8和Vr=3.3这两个均方根流速工况。而如果Vr,m对应的最大流速及均方根流速均介于[4,8]之间，仍表现为振荡流下的(A/D)max小于对应的均匀流工况。

5 结 论

本文尝试性地将现有受迫振动试验所得流体力系数库引入振荡流下柔性立管涡激振动时域预报模型，采用全新的锁定判定区间及锁定准则，通过与模型试验结果比较，验证了推荐方法的准确性及可行性。针对不同KC数及最大约化速度定义的振荡流下立管动力响应呈现的诸多有别于定常流条件的响应特性，本文从涡激振动发生机理层面进行了讨论总结。结合同一立管模型相关均匀流下的预报结果对比分析了振荡流与均匀流下结构动力响应，并参照振荡流下涡激振动机理分析，给出了相应的理论解释。本文研究得到结论如下：

(1) 用于模拟定常流下立管涡激振动的流体力系数库同样适用于振荡流工况。基于推荐预报方法的计算结果与对应的试验观测数据较为吻合，本文涡激振动时域数值模型可有效预报柔性立管定常流及振荡流条件下结构动力响应。

(2) 振荡流下立管涡激振动预报及试验结果均存在间歇涡激振动、振幅调制、迟滞、频率转换、高频谐振等现象并呈现一定的发展过程。不同KC数及最大约化速度组合下，涡激振动响应形式同样有所区别，上述响应特性均可通过对振荡流的幅值及周期进行分析讨论，结合涡激振动发生机理予以解释。

(3) 大KC数工况下，涡激振动的发展过程较为清晰，且随着最大约化速度的增加，锁定阶段占半个振荡周期的比例随之增大。振幅调制和频率转换呈现出与来流振荡周期对应的周期性和规律性。上述时变响应特性均是由于流速随时间变化并周期性进出涡激振动激励区和阻尼区所致。迟滞现象在KC数较大时也显现得较为明显。

(4) 小KC数工况下，振幅调制及频率转换现象同样存在，但振幅和频率的波动范围较小且无明显的涡激振动发展过程。由于流速变化较快，立管处于激励区和阻尼区的时间均太短以致于无法对涡激振动形成稳定的增强或减弱作用，结构响应呈现一定的不稳定性。KC数较小时，立管涡激振动响应特性与均匀流条件下较为相似，不再具有与来流振荡周期对应的周期性和规律性。

(5) 在流速近似的条件下，振荡流工况的涡激振动均方根位移大于对应均匀流工况的相关值。而当最大约化速度相同时，较小的KC数对应较大的涡激振动均方根位移。

综上，本文推荐时域方法可以针对定常流及振荡流下柔性立管的涡激振动响应给出合理的预报结果，亦可帮助加深对各类复杂背景来流情况下立管涡激振动特性的认识和理解，预报结果可为海洋细长结构物工程设计领域提供一定的参考。