济宁市山区设计洪水计算方法分析

2018-08-01赵长河时延庆

治淮 2018年7期

刘驰赵长河时延庆

（1.济宁市水利局济宁 272100 2.济宁市水文局济宁 272100）

1 流域概况

尚家庄流域位于山东省济宁市泗水县东南部山区，济河上游，泗张镇尚家庄，断面以上控制流域面积约61.99km2，流域内有一个雨量站——青界岭站，具有长系列降雨实测资料，上游有一个小（一）型水库——青界水库，青界水库的控制流域面积14.04km2。卢沟流域位于泗水县西南部山区，圣水峪镇卢沟村，断面以上控制流域面积约2.78km2，无实测降雨资料。两个流域平均坡度较大，属于山洪多发区，在济宁市具有较高的典型性。

2 设计洪水计算方法

2.1 设计暴雨计算方法

（1）有实测降雨资料的地区，可以直接选取以每年指定统计时段的最大面暴雨量进行频率计算，求得设计面雨量。面雨量统计参数的估计一般采用适线法，设计洪水规范规定，其经验频率公式采用期望值公式，线型采用皮尔逊III型曲线。统计参数可用矩法等方法初估，用适线法调整确定。推求出设计暴雨参数（均值、变差系数Cv、偏态系数Cs）后，即可计算出不同频率的设计暴雨量和时段雨量。

经验频率计算：对于实测降雨，在n项连序降雨系列内，按大小顺序排位第m项的经验频率Pm可按以下数学期望公式计算：

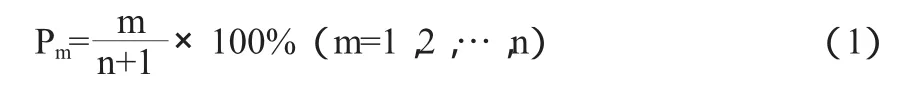
频率适线方法是先将历史实测暴雨系列按上述经验频率公式计算Pm值后，点绘在机率格纸上，其纵坐标为均匀分格的降雨量，横坐标与频率值的标准正态分布分位数有关。由于标准正态分布分位数在P=50%处为零，而海森机率格纸在P=0.01%时的横坐标值为零。

根据矩法初估的统计参数均值、变差系数Cv及偏态系数Cs（山东地区暴雨系列的偏态系数Cs通常取值为3.5Cv），求得对应于各频率的降雨量Hp后，点绘在频率纸上连成理论频率曲线，使理论曲线与实测点据相配，在适线时可调整计算的变差系数Cv，直到理论曲线与实测点据配合最佳为止（可适当照顾上部点据的配合）。调整后的均值、Cv、Cs值即为所求理论频率曲线的参数。

（2）在无实测降雨资料地区，可通过查《山东省水文图集（1975年）》获得有关设计暴雨参数。由多年平均年最大24h降水量等值线图查得暴雨参数，由年最大24h降水量变差系数（Cv）等值线图查得暴雨参数Cv，同样获得设计暴雨参数n1、n2等，进而计算出不同频率的设计暴雨量和时段雨量。

2.2 设计洪水计算方法

用推理公式法、瞬时单位线法和经验公式法分别进行设计洪水计算。查询山东省水文图集，Pa为40mm。针对上游有水库的计算单元，考虑水库的调蓄作用。

2.2.1采用推理公式法

根据《水利水电工程设计洪水计算规范》（SL44-2006），基本公式：

式中：Qm为洪峰流量，m3/s；h为在全面产流时，为τ时段的最大净雨；在部分汇流时，为单一洪峰的净雨，mm；F为流域面积，km2；τ为流域汇流历时，h；m为汇流参数；L为沿主河从出口断面至分水岭的最长距离，km；J为沿流程L的平均比降，以小数计。

表1可作为山东省山丘区在无资料条件下确定m值的参考，表中θ=L/Jl/3。2.2.2采用瞬时单位线法

表1 汇流参数表

瞬时单位线是流域上均匀分布的历时无限趋于零的单位净雨在流域出口断面形成的径流过程线。瞬时单位线的基本假设与一般时段单位线的不同之处在于其单位净雨时段无限趋于零，即为脉冲入流。瞬时单位线主要有两个参数，便于分析及地区综合，可以此为根据设计暴雨推求无资料地区洪水。

瞬时单位线在应用时，是根据两个参数转化成时段单位线，再根据相应时段的设计雨型，即可推求设计洪水流量过程。

查询《山东省水文图集（1975年）》，全省山丘地区Mi的公式为：

式中：0.196为一般山丘地区的，其他各类地区如表2；F为流域面积，km2；J为河道干流平均坡度；R为净雨深，mm，取各时段净雨深；tc为净雨历时，h，取净雨时段总历时。

计算流程：①以产流模型计算成果作为输入，计算各时段净雨对应的瞬时单位线参数Mi值。②由瞬时单位线参数Mi查出计算时段和该计算时段对应的时段单位线，各时段流量乘以面积比F/100即为本流域时段单位线。③将各时段的净雨乘上单位线得到该时段对应的流量过程数据，逐时段计算直到降雨结束。④将各时段净雨计算的流量过程数据，错时段叠加，加基流（每l00km2加1.0m3/s），得到最终的设计洪水过程数据。

2.2.3经验公式法

根据《山东省水文图集（1975年）》提供的洪峰流量经验公式推求相应的洪峰流量。计算公式为（山丘地区、平原面积小于70%的山丘平原混合区）：

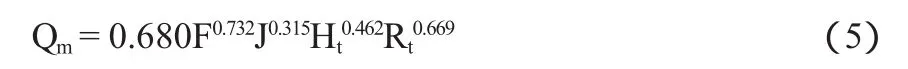
式中：0.680为一般山丘地区的，其他各类地区如表3；F为流域面积，km2：Rt为净雨深，mm；Ht为推求洪峰流量的设计流域平均降水量，mm；J为河道比降。

表3 山东省各类地区上式中的系数表

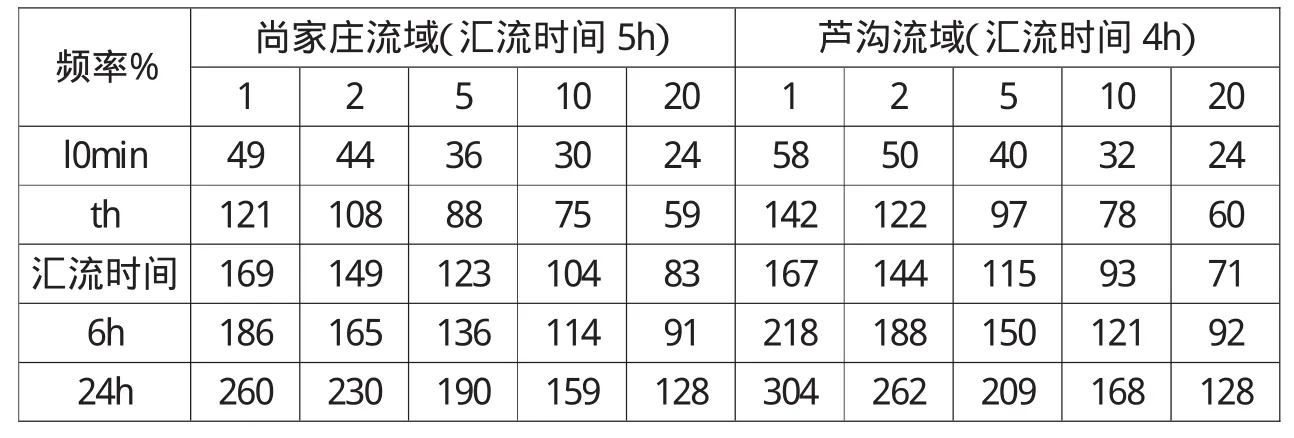
表4 各频率设计暴雨（面雨量）成果表（单位：mm）

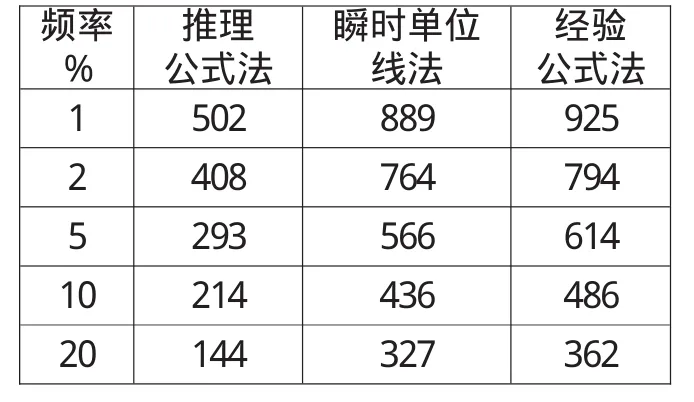
表5 尚家庄流域三种方法的计算成果表（单位：m3/s）

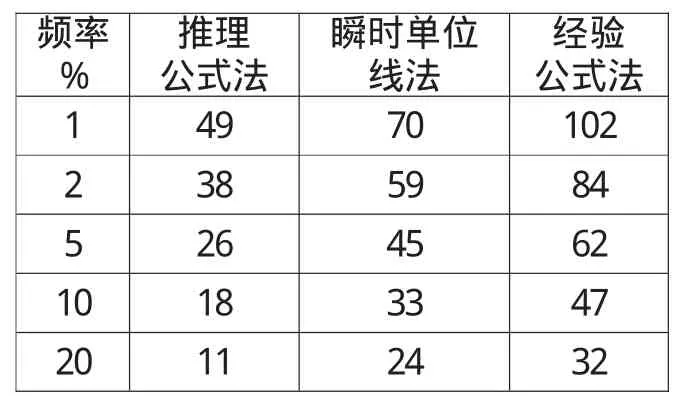
表6 卢沟流域三种方法的计算成果表（单位：m3/s）

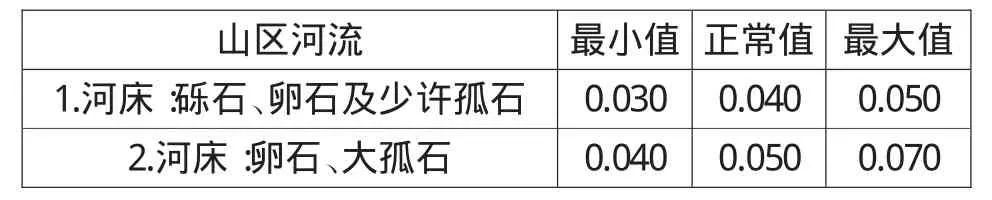
表7 天然河道糙率取值表

表8 尚家庄流域百年一遇设计洪峰水位对照表（单位：m）

式中：H24为设计频率的年最大24h降水量，mm；n2为短历时暴雨指数。

2.2.4水库的调蓄作用

如果防灾对象上游有水库，则考虑水库的调蓄功能。当发生降雨时，来水流量等于下泄流量，若超过水库最大下泄流量，则按最大下泄流量处理，下泄不掉的洪水视为水库拦蓄洪水。

3 设计洪水计算

3.1 设计暴雨

根据上述设计暴雨计算方法，尚家庄流域和卢沟流域设计暴雨成果见表4。

3.2 设计洪水

根据上述设计洪水计算方法，分别进行尚家庄流域和卢沟流域设计洪水计算，三种方法的计算洪峰流量成果对比见表5和表6。

4 合理性分析

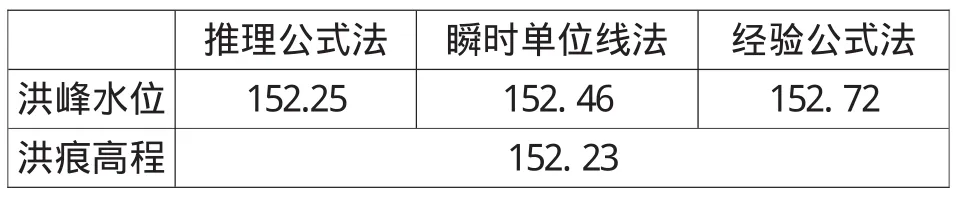
表9 卢沟流域百年一遇设计洪峰水位对照表（单位：m）

拟采用曼宁公式法计算两个流域设计出口断面各设计流量相应的洪水位，与实测历史洪痕水位进行对照，选定成果最接近的方法。

曼宁公式如下：

式中：Q为流量，m3/s；A为过流断面面积，m3；V为过流断面平均流速，m/s；n为糙率，参考《山洪灾害分析平均工作方法指南》，见表7；R为水力半径，m；J为水面比降。

经计算，两个流域设计出口断面各设计流量相应的洪水位，与实测历史洪痕水位进行对照见表8、表9。

由表8和表9可以看出，瞬时单位线法和经验公式法比推理公式法计算出来的结果及实测洪痕高程大很多，推理公式法计算成果与实测洪痕高程较为接近。由于瞬时单位线和经验公式是1975年版的《山东省水文图集》根据20世纪50～60年代的水文资料整理出来的，年代较为久远，序列长度较短，数值偏大。因此选用推理公式法计算设计洪水较为合理。