基于遗传粒子群融合算法的泵站经济运行研究
2018-08-01文蓓蕾
文蓓蕾 李 频
(1.上海交通大学电信学院 上海 200030 2.江苏省泰州引江河管理处 泰州 225300)
1 引言
泰州引江河是南水北调东线工程中一个重要取水口,以引水为主,集灌溉、排涝、航运、生态、旅游等功能于一体,既是南水北调的水源工程,也是开发“海上苏东”的战略性工程,是江苏水利的标志性工程之一。而高港枢纽则是这一工程的控制口门。建站以来,增加了南水北调的供水能力,提高了里下河地区和通南地区的灌排标准,为苏北地区改善水质、沿海冲淤保港、实施滩涂开发提供了充足水源。在实现“工程水利”向“资源水利”转变的过程中,有必要采取非工程措施来挖掘泵站的潜力,通过泵站的优化调度与控制来达到高效、节能、经济运行的目的。对于泵站经济运行问题,已有不少学者做了有益的探索,为计算方便,本文以泵站轴功率最低进行研究,求解模型近年来受到广泛关注的遗传算法。
2 泵站优化运行的数学模型
2.1 水泵性能曲线拟合
水泵特性曲线反映了水泵各个性能参数之间的相互联系及变化函数关系,是科学调节水泵运行的必备条件。本文研究的水泵机组的基本性能曲线采用已广泛应用且有足够精度的二次曲线进行拟合:

式中:HN、PN、ηN、QN分别为水泵额定转速下的扬程、轴功率、装置效率、流量;a1、b1、c1、a2、b2、c2、a3、b3、c3为待定系数。不同机组不同叶片角度可拟合出其对应的特性曲线方程。
2.2 泵站优化调度分解协调模型
本文研究的泵站同时存在着两种不同调控性能的机组,所以引入大系统理论,将该泵站分解为两个相对独立的子系统:第一子系统,由全调节机组组成;第二子系统,由半调节机组组成,建成如图1所示的二层递阶分解协调模型。
2.2.1模型1
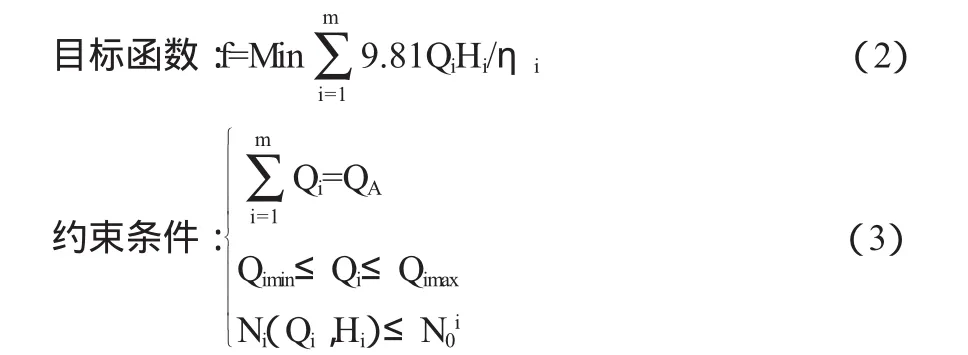
2.2.2模型2
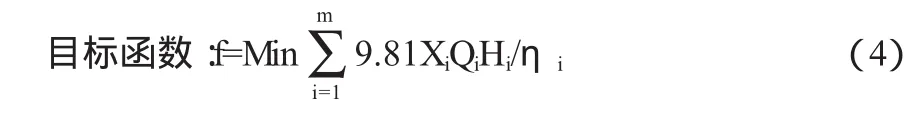
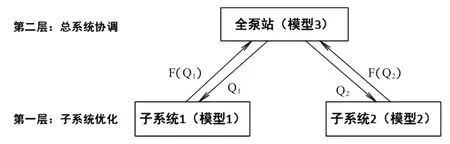
图1 泵站优化调度分解协调模型图
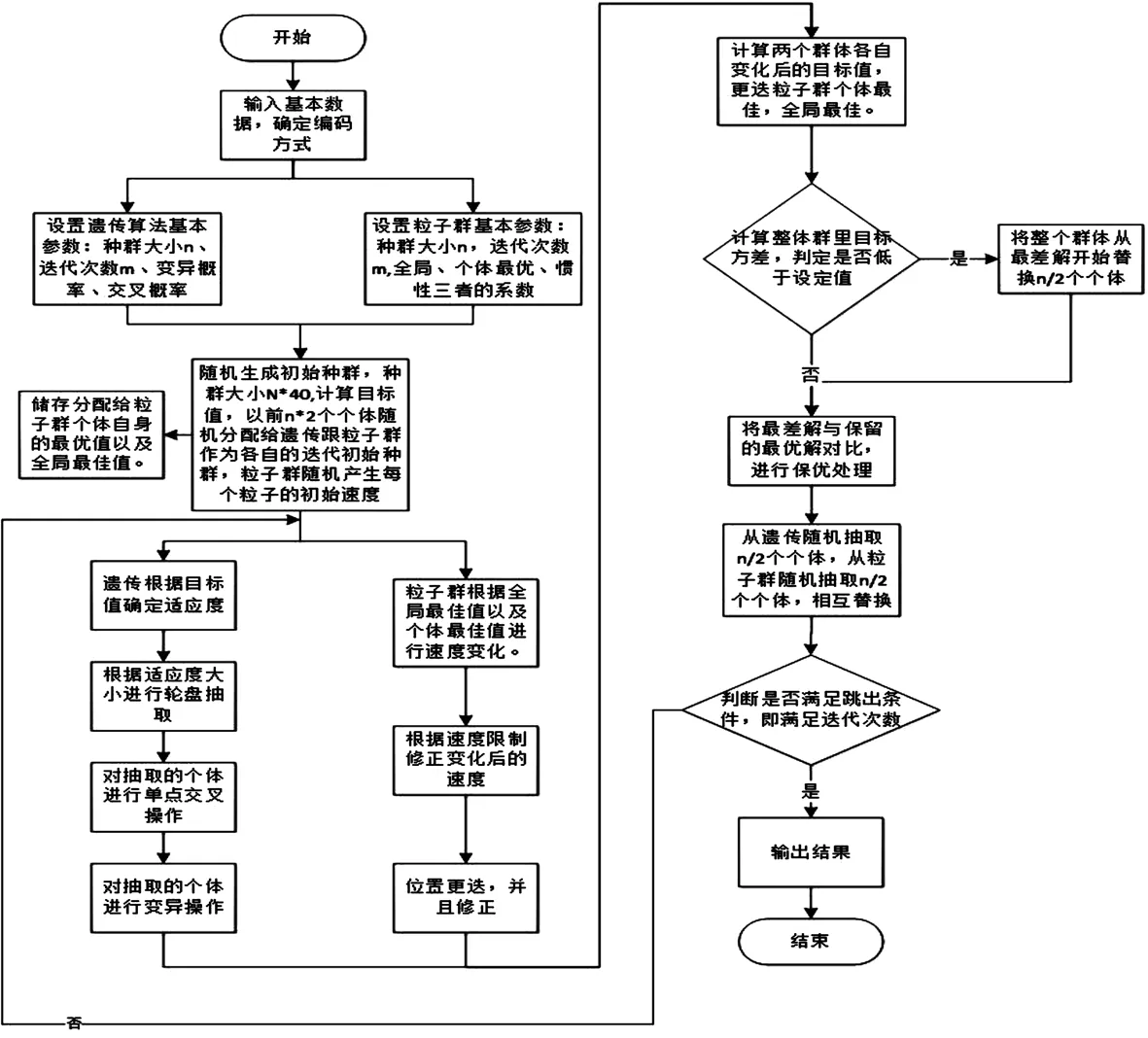
图2 GA-PSO算法流程图
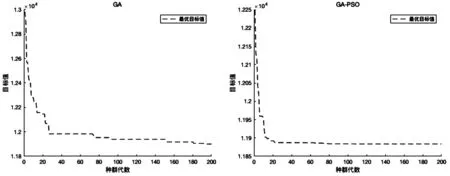
图3 GA算法和GA-PSO算法的迭代曲线图

式中:Qimax、Qimin为第i台机组的最大和最小抽水流量;为第i台机组输入功率,N0i为允许的最大输入功率;m为半调节机组数;QA为模型第二层分配给该子系统的流量;Q0i和N0i分别为给定工作水头下第i台定桨机组的额定抽水流量和抽水功率;QB为模型第二层分配给该子系统的流量。
2.2.3模型3

式中:Q为整个泵站本次调度的总流量;CA和CB分别为子系统1、2抽排单位流量时的功率耗费;fi为第i个子系统承担Qi流量时的最小功率耗费。
3遗传算法和粒子群算法
3.1 遗传算法
遗传算法(Genetic Algorithm,GA)是一类借鉴生物界的自然进化规律演化而来的随机搜索方法,由美国Holland教授于1975年首次提出。算法采用“适者生存、优胜劣汰”的进化原则,对包含可能解的种群反复使用遗传操作(包括选择、交叉和变异),使种群不断进化,以求得满足要求的最优解。目前遗传算法已成功应用到许多领域,如优化设计、神经网络训练、模式识别、时序预测等。
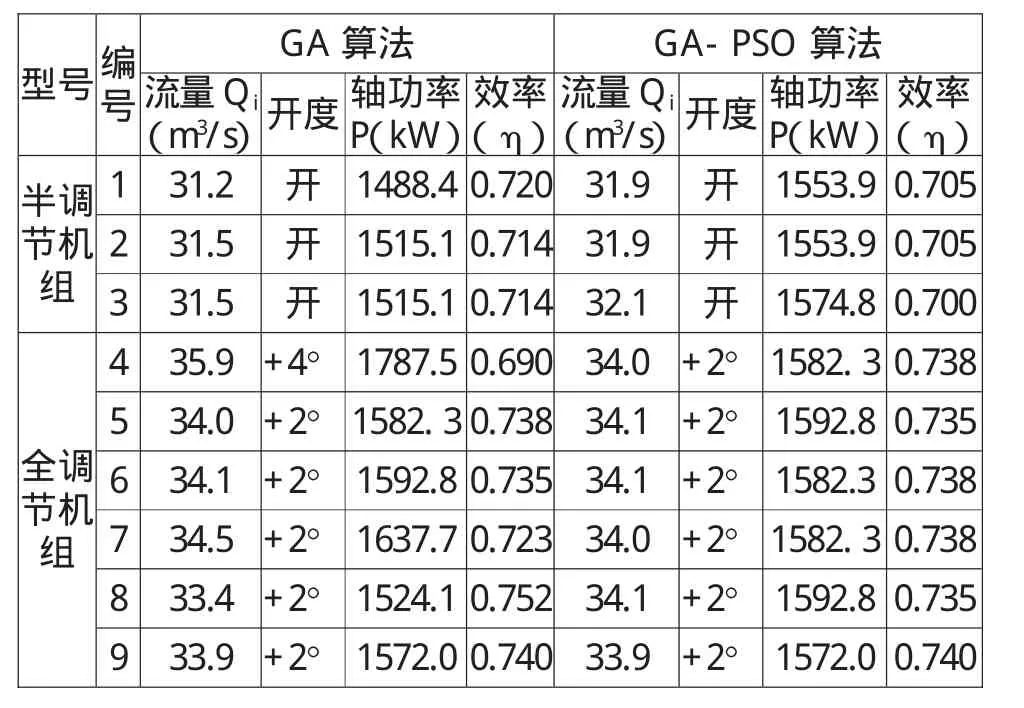
表1 GA算法和GA-PSO算法仿真结果表
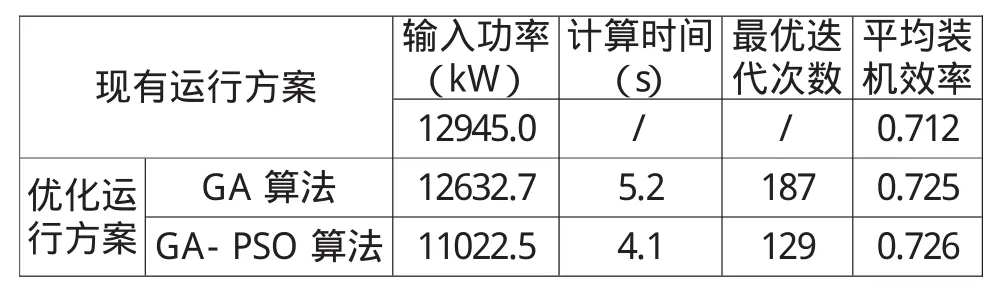
表2 优化运行方案与现有运行方案对比表
3.2 粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)是Kennedy和Eberhart于1995年提出的一种新型群体智能优化算法,源于对鸟群觅食行为的研究。在PSO算法中,每个粒子的位置代表着搜索空间的一个候选解,粒子有位置和速度两个特征。粒子位置坐标对应的目标函数值作为粒子的适应度。算法首先初始化一群随机粒子,然后通过迭代找到最优解。粒子群优化简单易实现、收敛速度快,在工程优化、图像处理等诸多领域得到了广泛的应用。
4 遗传粒子群融合算法
本文将遗传算法和粒子群算法以同等地位进行并联混合,将种群一分为二,遗传算法和粒子群算法各进化一半的个体,遗传算法的选择、交叉、变异过程保证了解的多样性,粒子群算法的单一寻优模式提高了寻优速度,同时,粒子群算法中粒子有记忆,当前最优解所有粒子都保存,避免运算陷入局部极值点的束缚,利用使每一步的迭代都优于单一的遗传算法和粒子群算法,进而提高了算法整体的性能。与其他混合最优化算法不同的是,该算法没有破坏粒子群和遗传算法的独立性,而是通过全局最优样本把两个算法有机地结合在一起,因此新算法在具备了原有算法优势的基础上,获得了更好的寻优性能及寻优稳定性。GA-PSO算法流程图如图2所示。
5 仿真实验
本文以高港泵站为例,该泵站共安装9台立式开敞式轴流泵,单台最小抽水流量为26m3/s,最大抽水流量为42m3/s。其中 1#~3#机组为半调节轴流泵,4#~9#机组为全调节轴流泵,可在-4°~+4°之间连续可调,9台水泵配套电机均为2000kW立式同步电动机。抽水指标要求:泵站出口总流量Q=300m3/s,出口扬程H=3.5m。
本文利用MATLAB软件进行仿真实验。参数设置为:种群取50,迭代次数取200,交叉概率取0.5,变异概率取0.2。为了说明遗传粒子群融合算法的有效性,分别使用基本遗传算法和遗传粒子群融合算法作对比实验,运算结果如表1所示,对比数据分析如表2所示,迭代曲线如图3所示。
由表1、表2可知,两种算法的求解结果都比现有运行方案轴功率低,这说明本文提出的优化方案具有显著的优化效果;对比传统GA算法和GA-PSO算法迭代200次运算时间、寻得最优解的迭代次数和输出的最优解,后者明显运算时间更短,寻得的最优解更优;图5非常直观地体现了GA-PSO算法相较于GA算法寻求最优解的能力更强、效率更高。
以上仿真实验结果说明,本文提出的基于遗传粒子群融合算法的泵站经济运行模型和方法是可行的,且相较于传统遗传算法有更好的寻优能力和更快的搜索速度,具有较好的实用价值。
6 结语
本文针对高港泵站有不同调控性能机组的实际情况,对水泵机组的动力特性曲线进行了拟合,以泵站总耗能最小为目标,建立了泵站优化调度的二层分解协调模型。针对该模型的复杂性,提出了一种工程实用的遗传粒子群融合算法进行求解。同时对比传统遗传算法的求解结果,得出遗传粒子群算法具有更好的寻优能力和更快的搜索速度。因此本文的研究成果对实现泵站优化运行、提高经济效益、节能有较好的现实意义
