基于BP神经网络和遗传算法的GIS分合闸故障分类方法

2018-07-31付光晶于跃张峰张士文

电气自动化 2018年2期

付光晶，于跃，张峰，张士文

(上海交通大学电子信息与电气工程学院，上海 200240)

0 引言

GIS作为气体绝缘全封闭组合式电器设备，与普通的高压变电站设备相比，具有体积小、空间利用率高、故障率小、运行安全性高的特点，因此目前在高压、超高压和特高压领域被广泛应用。但是由于其密封式的结构设计，也带来了故障定位困难，检修流程繁杂，事后断电时间久，断电范围大等缺点。对于GIS频发的分合闸故障，传统的对设备进行定期定点故障检测和修理的方法已经不能满足设备自身的工作要求，因此设计出一种能够快速准确分析GIS分合闸状态的方法便具有了重要的意义。

目前对于GIS分合闸故障检测的方法主要是在设备分合闸动作时对激励线圈中的驱动电流进行采样，然后再利用相应的算法对采样的电流波形进行故障分析。例如华中科技大学的易慧于2006年提出了最小二乘法和小波理论可以对分合闸电流进行故障分析[1]。浙江大学的曹飞于2008年采用分散包络统计法对分合闸线圈电流波形的轮廓进行综合分析和研究[2]。江苏财经学院的宋锦刚于2011年提出了将分合闸信号进行小波分解后对固定频段的信号重构，然后利用相似性原则对故障信号进行分类的方法[3]。上海交通大学的黄志于2015年利用核主元分析法对分合闸线圈电流波形特征值进行降维，再利用支持向量机对故障波形进行分类[4]。本文借鉴和参考了国内外学者对同类课题的研究成果，针对以往算法中模型复杂，预测精度差等缺点，依据GIS分合闸经典波形的特征点搭建了BP神经网络，并利用遗传算法和大量的样本对神经网络进行优化和训练，实现了GIS分合闸故障的有效分析和精准分类。

1 GIS基本特性和故障分析

1.1 正常分合闸电流波形

图1显示了GIS正常分合闸时驱动线圈上的经典电流波形[5]285，整个分合闸过程可以被分为4个阶段，其中T1～T2阶段为线圈初始通电阶段，此时电流按照指数形式上升，但由于铁芯受到的机械阻力大于电磁力，铁芯无法运动。随着通电线圈内的电流的不断增加，到达T2时刻时，铁芯的电磁力将和其受到的阻力相等，此时铁芯处于运动的临界状态，随后在T2～T3阶段铁芯在电磁力的作用下开始做加速运动并产生反向感应电动势，使得线圈电流减小，直至铁芯在T3时刻触碰到分合闸触发器后停止运动，此后线圈电流会在T3～T4阶段再次以指数形式上升，直至T4时刻铁芯能够推动脱扣装置脱扣，脱扣后，分合闸弹簧将释放弹性势能，带动断路器本体迅速动作，在T4～T5阶段辅助开关将开始动作，产生电弧，此时电压迅速升高，电流将迅速减小到最初值。

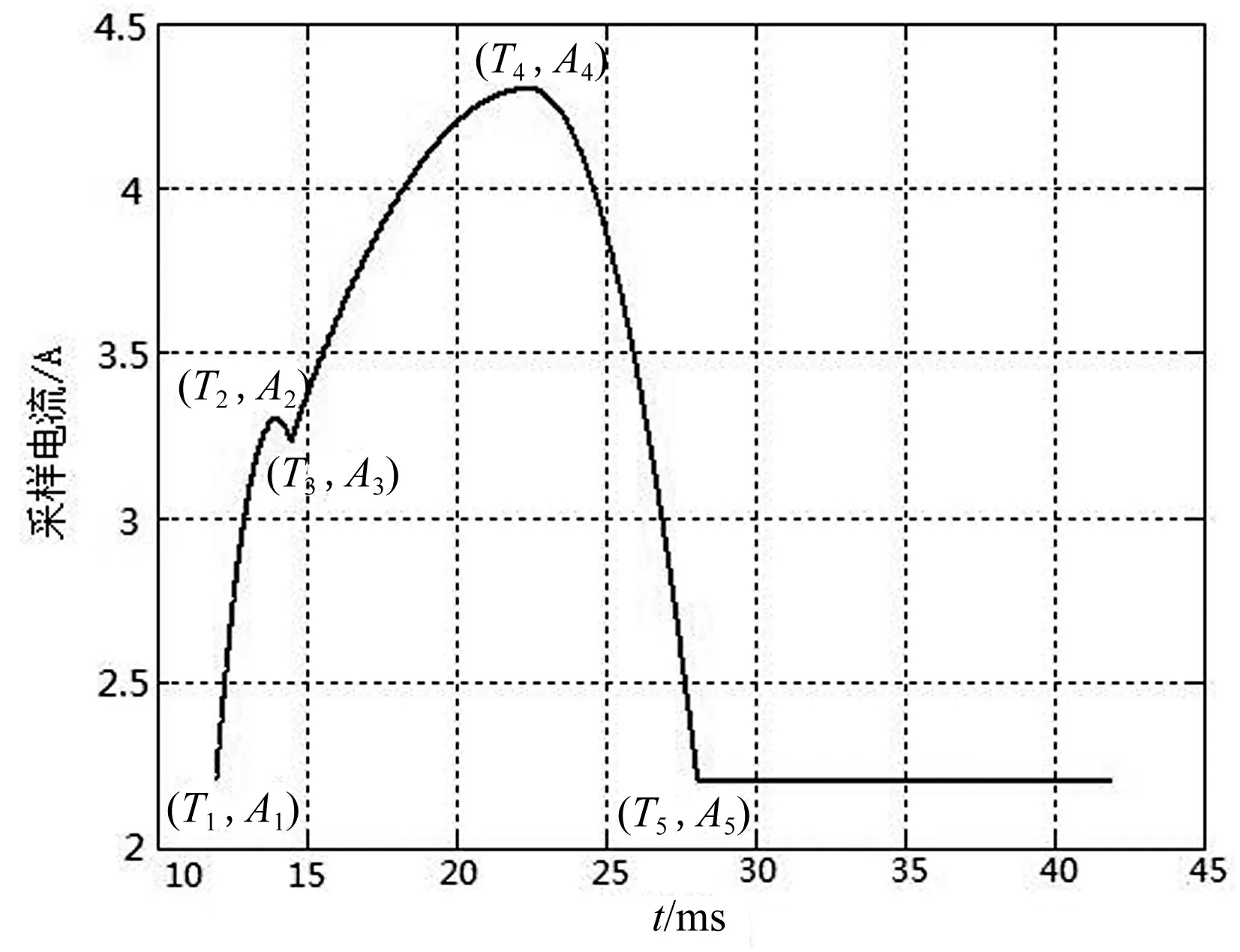
图1 正常分合闸情况下线圈电流波形

从图中可以看到，分合闸过程中线圈电流波形存在三个极值点，分别出现在T2，T3，T4三个时刻，其中T2时刻是铁芯动作的临界点，T3时刻铁芯撞击到分合闸触发器，T4时刻脱扣装置脱扣，这三组极值点的数值大小对于分析分合闸故障具有非常重要的意义。

1.2 脱扣卡滞或过软电流波形

图2显示了出现脱扣卡滞或者脱扣过软情况时线圈电流的变化趋势，大量试验证明，机构老化和润滑过度经常是导致分合闸出现脱扣问题的主要原因[6]。当GIS设备出现老化时，脱扣装置卡滞会延长T3～T4区间的时间，此时线圈电流达到第二个峰值的时间会加长，也会间接导致电流的峰值增大。相反，当GIS设备出现润滑过度时，脱扣装置过软会缩短T3～T4区间的时间，此时线圈电流达到第二个峰值的时间会缩短，其电流的峰值也会小于正常分合闸时的情况。

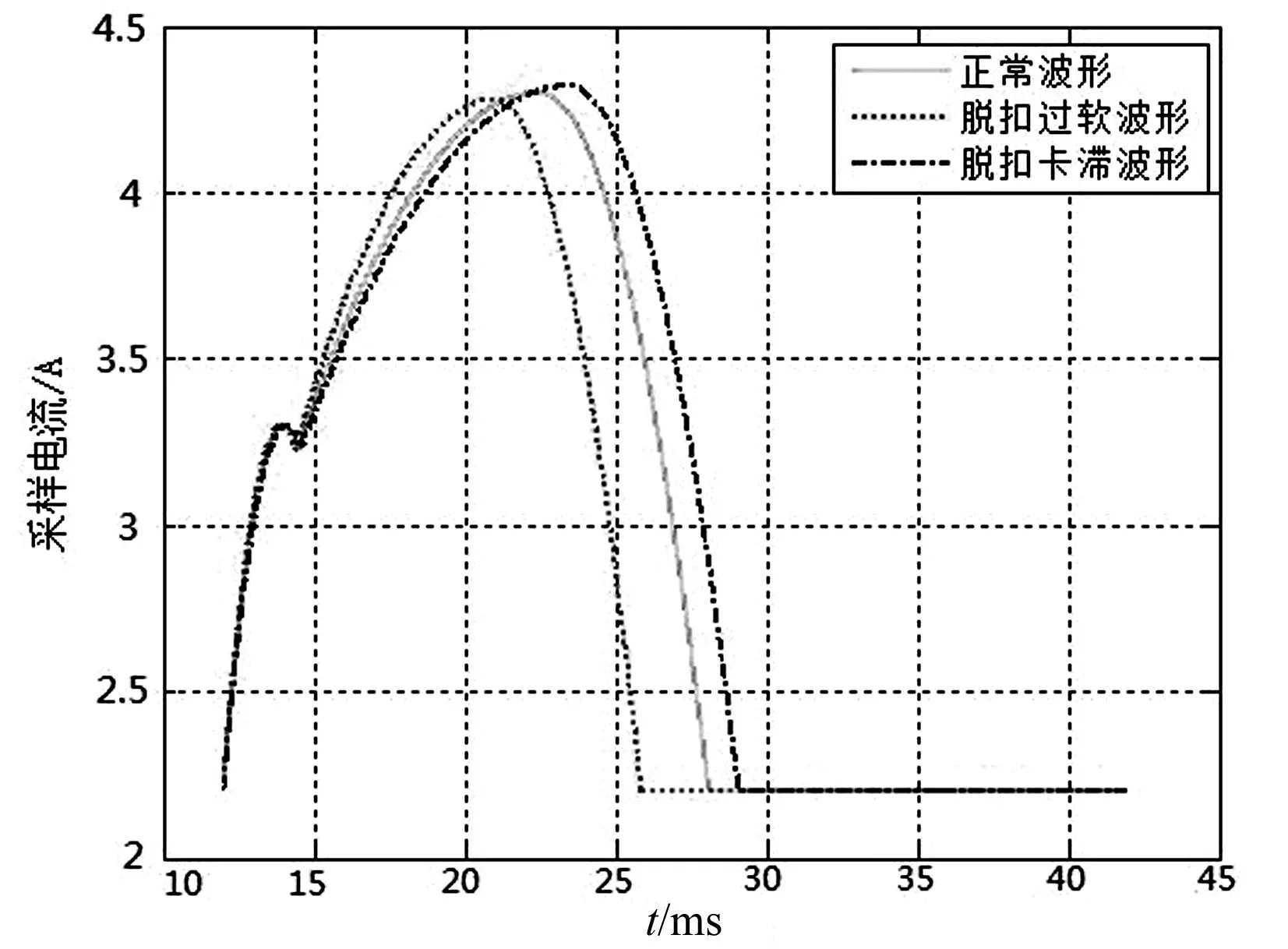
图2 脱扣卡滞或过软情况下线圈电流波形

1.3 供电电压过高或过低电流波形

图3显示了当供电电压高于或低于正常值时线圈电流的变化趋势，大量试验表明，当供电电压过高时，由于设备的等效电阻没有变化，此时激励电流的增长速度会快于正常情况，铁芯产生的电磁力会大于正常值，从而导致铁芯的临界运动时间和脱扣装置的脱扣时间提前到达，使得分合闸线圈电流的波形被整体抬升。相反，当供电电压不足的时候，激励电流的增长速度会慢于正常情况，铁芯产生的电磁力会小于正常值，从而导致铁芯的临界运动时间和脱扣装置的脱扣时间延缓到达，使得分合闸线圈电流的波形被整体拉低。

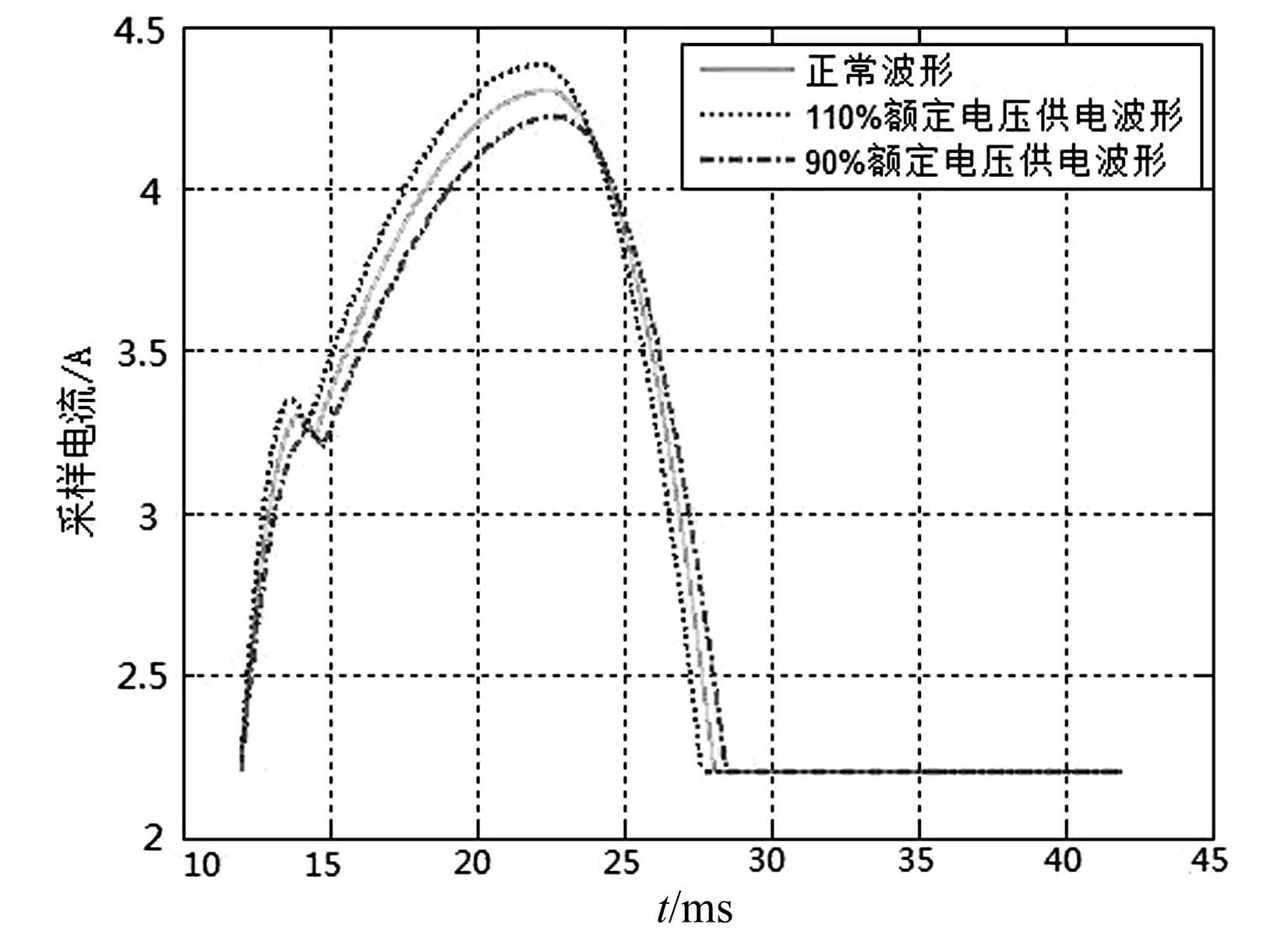
图3 供电电压过高或过低情况下线圈电流波形

2 BP神经网络结构设计

2.1 BP神经网络原理

BP神经网络是目前应用最为普遍的一种神经网络，其网络的拓扑结构一般包含输入层，隐藏层和输出层，其中隐藏层又以单隐层应用最多。BP神经网络的训练由输入信号的正向计算和输出信号的反向回馈组成，当输入信号经过网络计算后，其网络输出与期望输出之间有误差时，我们可以将误差定义为:

(1)

式中:dk代表了输出层第k个神经元的期望输出;ok代表了输出层第k个神经元的实际输出。将上式展开到隐藏层，有:

(2)

式中:函数f代表了从隐藏层到输出层的转移函数;wik代表了隐藏层第i个神经元到输出层第k个神经元的网络权值;yj代表了隐藏层第j个神经元的网络输出。

BP神经网络对权值调整的原则是使输出误差不断减小，因此权值调整量被定义为与输出误差的负梯度成正比关系，即:

(3)

(4)

式中:w和v分别代表了隐藏层到输出层的权值和输入层到隐藏层的权值;负号代表了权值按照负梯度下降;常数η代表了神经网络的学习速率，其一般定义为(0,1)中的一常数。对上述两式继续推导，可得:

(5)

(6)

式中:对输出层均有j=0,1,…,m;k=1,2,…,l;对隐藏层均有i=0,1,…,n;j=1,2,…m;f′(netk)代表了输出层转移函数对输出层第k个神经元的偏导数;f′(netj)代表了隐藏层转移函数对隐藏第j个神经元的偏导数。

利用上述公式即可对网络权值和神经元阈值进行一次调整，反复利用样本数据对神经网络进行训练即可使神经网络误差不断收敛以致达到理想状态。

2.2 BP神经网络算法设计

在本设计中，根据GIS分合闸电流波形的特点，建立三层且隐藏层神经元个数为10的神经网络。图4展示了本神经网络系统的整体结构，其中神经网络输入层对应分(合)闸线圈电流波形中三组极值点处的6个特征值，输出层对应分合闸动作后设备的5种状态类型。设备的状态类型和其对应的标签值如表1所示。

图4 BP神经网络结构

故障类型电压过高电压过低正常情况脱扣过软脱扣卡滞标签值-4-2024

本设计中输入层到隐藏层和隐藏层到输出层的转移函数都设置为Sigmoid函数，学习效率η设置为0.2，权值引用动量表达式ΔW(t)=ηδX+αΔW(t-1)，其中α=0.2，利用神经网络对GIS分合闸故障判断的算法流程图如图5所示，其一共分为以下几个步骤:

第一步，搭建三层BP神经网络，并为神经网络权值和神经元阈值设置初始值，设置转移函数和学习效率。

第二步，将GIS所有的分合闸线圈电流样本输入到神经网络中，经过神经网络拓扑结构计算得到输出值，并利用式(1)计算出样本标签值和实际输出之间的误差。

第三步，利用式(2)～式(6)和第二步得到的误差值对网络的权值和神经元阈值进行负梯度调整，并反复迭代，直至达到训练次数。判断误差值是否达到精度要求，如果没有达到则重新进行训练，如果达到了则表明训练过程结束。

第四步，将测试样本代入训练后的神经网络中，利用输出值与设定标签值之间误差判断神经网络的性能。

图5 BP神经网络整体流程图

3 遗传算法优化设计

3.1 遗传算法的引入

对于上节利用神经网络进行故障分类的算法，虽然其结构简单且易于操作，但是却具有一些天生的缺陷，例如误差经常仅能收敛到局部极小点而无法达到全局最优点，这种问题经常是由于神经网络的初始权值和神经元阈值设置不当而导致的。针对这些问题，可以用遗传算法来进行优化。遗传算法的原理是将问题的待求量转化成二进制染色体，然后在问题求解的过程中，反复根据“适者生存”的原则对染色体进行选择，交叉和变异，以此来交换染色体的基因，使其能够达到最优解。

3.2 遗传算法优化的实现

图6展示了如何利用遗传算法对基于神经网络的GIS故障分类方法进行优化，其主要算法流程分为以下几步。

第一步：建立神经网络，设置神经网络参数，将GIS分合闸线圈电流样本归一化。

第二步：为神经网络的连接权值和神经元阈值进行二进制编码，并将其连接成串组成一个个体，随机生成40组这样的个体组成一个种群，针对种群中的每个个体对应的神经网络，分别将归一化后的样本输入并计算网络输出值。

第三步：利用网络输出值计算适应度函数值，根据适应度函数值对样本重新选择，对于适应度不高的个体进行淘汰，随后对种群中的个体进行交叉和变异以丰富种群特性。

第四步：将进化过的离散种群中的每个个体的数值重新赋值给神经网络权值和神经元阈值，针对新种群中的由每个个体组成的神经网络，再次输入样本计算子代的目标函数值。

第五步：根据子代的目标函数值，将子代个体选择性的插入到父代样本中。

第六步：遗传代数计数器加1，判断遗传代数是否达到设定数值，如果没有达到，返回步骤三继续进行进化，如果达到了，输出每次进化后的误差值。

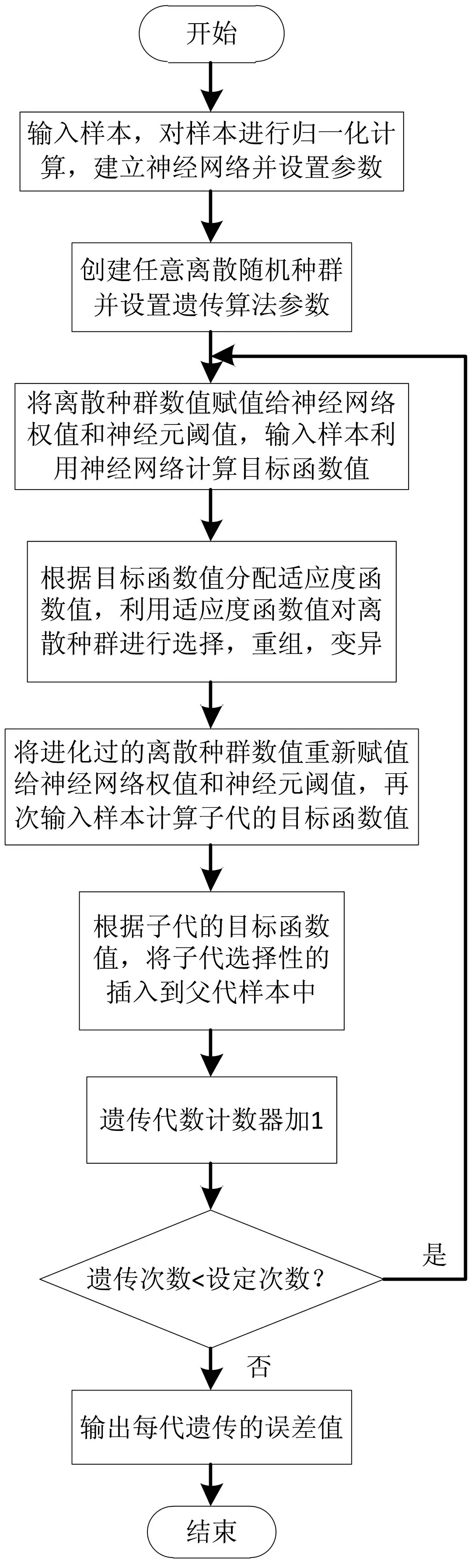
图6 遗传算法优化设计流程图

4 试验过程和结果

对于GIS分合闸过程中线圈电流的一些经典特征值，经过对文献[5]289的查阅将其列在表2中，从表2的数据可以发现其特征值的变化趋势与第1节所描述的电流波形特性基本一致。其中(T2，A2)对应铁芯动作临界点的时间和线圈电流，(T3，A3)对应铁芯撞击到分合闸触发器的时间和线圈电流，(T4，A4)对应脱扣装置脱扣的时间和线圈电流。

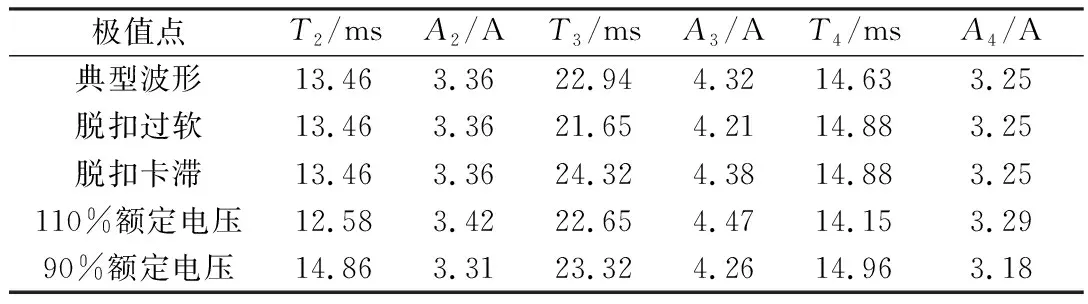
表2 GIS分合闸线圈电流经典特征值

利用表2中的经典特征数据，针对每种分合闸情况拟合40组特征点，并将前20组用于神经网络的训练，后20组用于训练后神经网络的性能测试，表3为抽调的100组训练样本中的5组，并分别将不同的分合闸电流特征值赋予相应标签值。

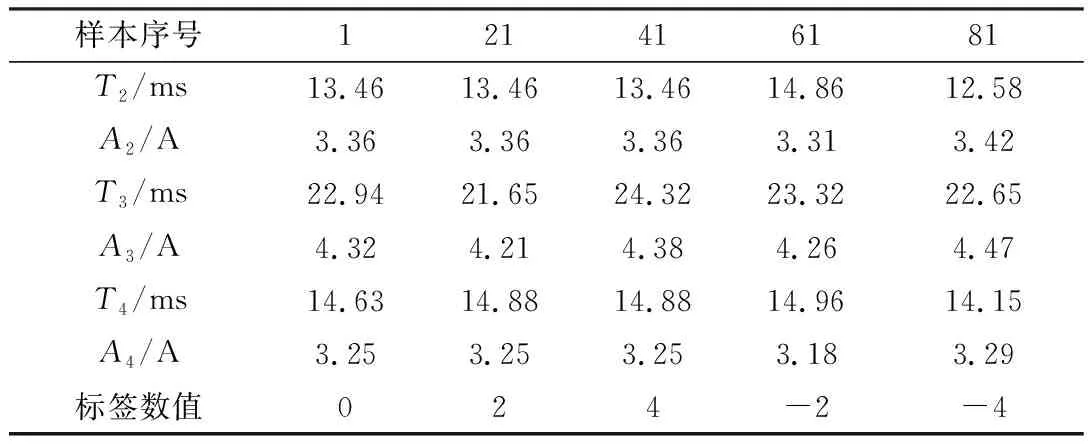
表3 神经网络训练样本抽调

将100组数据点输入到神经网络中经过100次训练后，可以得到相应的网络参数，输入层和隐藏层之间的权值系数V为:

其中权值矩阵V的第i行第j列元素对应的输入层的第i个神经元和隐藏层的第j个神经元之间的权值大小。而隐藏层和输出层之间的权值系数W为:

W=[0.407 -0.138 -0.059 -0.369 0.014 -0.501 0.079 -1.180 0.005 0.208]T

权值矩阵W的第k列元素对应的隐藏层的第k个神经元和输出层神经元之间的权值大小。此外，经过神经网络训练的还有隐藏层和输出层的阈值，经过训练后其值为:

T1=[-2.352 2.112 -1.784 -0.719 1.031 -1.140 -0.289 -2.303 -2.057 -1.530]TT2=-0.235

至此，经过100次训练的神经网络已经形成，图7展示了在100次神经网络训练的过程中，输出误差的变化情况。

图7 BP神经网络训练过程误差变化

从图7中可以看到，神经网络误差值在前10次训练过程中收敛迅速，但是在第10次到第50次之间速度变缓，直到训练到53次时，神经网络的网络权重和神经元阈值进入到极小值区域，网络趋于稳定。网络经过100次训练后其输出与期望值的误差为1.824。图8显示了经过50次进化后，每次进化过程中种群中适应性最优个体经过100次训练后对应的误差值。

图8 遗传算法进化过程中误差的变化

在拟定遗传算法参数时，将子代和父代之间的代沟设置为0.95，这样可以保证误差随着遗传代数的变化持递减性的变化。图8显示出当种群进化到22代时，其误差值已经达到0.119，在随后的的进化过程中误差值没有再缩小，对比单独利用神经网络进行故障分类时，当训练到53次便进入极小值区域且误差值为1.824，其性能有了极大的提高。

针对训练结束后的神经网络，本试验利用剩余的100组样本对网络性能进行测试，表4抽调了100组测试样本中的5组。