基于差分进化PID控制的同步发电机励磁系统研究

陈金，张孝，王平，闵国君，李颖杰，陈峰

(1.贵州电网电力调度控制中心,贵州 贵阳 550002；2.南京南瑞继保工程技术有限公司,江苏 南京 211102)

0 引 言

灵敏准确的发电机励磁调节系统对于维持系统的电压稳定、减小发电机故障损失等方面具有重要作用。目前PID控制仍然是其主要控制方法。常规的PID控制器具有结构简单，稳健性好，容易实现等优点，能满足一般工业控制的要求[1-2]。

新能源的快速发展增加了电力系统的复杂性，同时对发电机的励磁控制提出更严苛的要求，普遍采用的PID控制技术，其控制性能很大程度上取决与PID参数的优劣。因此，不少学者尝试利用智能控制来优化PID参数，譬如将模糊控制与PID控制结合，优点是无需数学模型，结构简单，实现方便，但关键的模糊规则设计，依赖主观经验，在工况突变情况下，不能保证控制性能的稳定[3-4]。文献[5]将神经网络用于PID优化，神经网络的优势是对复杂非线性系统的拟合能力，但计算量大、实现困难是其缺陷；文献[6]采用粒子群算法优化PID参数，粒子群算法速度快，精度高，但算法需要设置的参数多，不稳定，易早熟。差分进化算法(Differential Evolution，DE)作为一种新的进化算法，因其在国际算法比赛中的优异表现而受到关注，其采用基于差异的变异操作，提高了进化效率。相比于粒子群优化，DE所需参数少，同时因为进化策略中计及了变量相关性，对于发电机非线性环节中的多变量耦合问题具有明显优势[7-8]。

本文根据励磁调节系统的综合性能指标，应用差分进化算法优化励磁控制器的PID参数，并将优化得到的结果，在电力系统模拟实验装置上进行验证。

1 励磁系统数学模型

同步发电机励磁系统基本由励磁控制、功率放大、发电机本体和电压反馈等环节组成，其主要作用是根据系统负荷变化调节励磁电流，目标是控制机端电压和无功分配，保证并列发电机的动态与静态稳定[9-10]。从研究励磁系统动态特性的角度出发，采用工程近似的办法，功率单元、测量单元和发电机均可简化为一阶惯性环节，励磁系统数学模型如图1所示。当系统电压改变时，励磁调节系统通过指定电压U*与反馈测量电压u的比较，得到电压偏差，经PID调节后再将控制信号放大，控制同步发电机的输出电压，直至机端电压达到稳定。图1中KG、KC、KA分别为发电机、测量单元和功率放大单元的增益，Td0、TR、TA为其时间常数。

图1 发电机励磁系统数学模型

2 差分进化PID控制器设计

2.1 差分进化算法

差分进化算法基本流程：假设有M个待优化参数，则NP个M维向量Yi，G(i= 0，1，2，…，NP-1)构成一个个体，这里G为代数，i为个体标号。

1)初始种群的产生

初始种群是在设定的空间内随机产生的，对种群内的每个个体计算其适应度。适应度函数通常是最小值函数，因此适应度越小越好。所有个体运算后适应度值最小的个体为当前最优个体，记为Ybest,其适应度值记为Vbest。

2)进化过程

(1)变异。目的是使当前一代的所有向量Yi，G都增加一个扰动向量：Vi，G+1=Ybest+F·(Yr1，G—Yr2，G) 。其中整数r1，r2∈[0，NP-1]是随机产生的，并且i≠r1≠r2。缩放算子F是控制变量(Yr1，G—Yr2，G)的放大倍数。因为Yr1，G、Yr2，G在抽取时的随机性，所以Vi，G+1的产生与Yi，G保证了相对独立性。

(2)交叉。交叉是制造新个体的主要操作。为此对Yi，G和Vi，G+1进行交叉操作，产生向量如下：

Ui,G+1=(U0,i,G+1，U1,i,G+1，…，UD-1,i,G+1)

(1)

其中

(2)

式中:j=0，1，…，D-1，rand是一个在[0，1]均匀分布的随机数；R(i)是一个随机整数且R(i)∈[0，D-1]；交叉概率CR∈[0，1]。交叉操作得到的新个体，丰富了种群的多样性。

(3)选择。作为新的个体Ui,G+1并不能自然成为下一代种群的新个体Yi,G+1，还需要和Yi,G竞争。竞争策略：计算二者的适应度值，性能更优的个体最终延续至下一代。全部的变异、交叉和选择操作构成了一次完整的进化。

DE算法的控制参数很少，只有缩放算子F、种群规模NP及交叉算子CR，参数设计是否得到，对算法性能有重要影响。

个体变异中扰动向量的大小由缩放算子F决定，在种群多样性和收敛性上起到平衡作用[11]。本文根据优化不同阶段对多样性和收敛性的不同要求，采用递减方法调整F：

(3)

式中:m为进化代数的当前值;M为进化代数的最大值;Fmax,Fmin分别为缩放算子F的上下限。这个方法的思路是优化初期需要扩大搜索范围，增加搜索到最优解的机会，这时F应当取大一点，越到后期，期望能在局部范围进行更细致的搜索，更快得到最优解，此时F应该设置小一些。

交叉算子CR决定了交叉操作产生新个体的几率。由式(2)可知，CR的取值增大，Vi，G+ 1出现在Ui，G+1向量中的几率增加，局部搜索能力增强，收敛速度快；反之，则Yi，G出现在Ui，G+1向量中几率增加，全局搜索能力增强，种群多样性好。因此为了兼顾多样性和收敛速度，采用递增算法：

(4)

式中：CRmin=0.1;CRmax=0.9。CR取值较小，种群多样性得到保证，CR随着搜索深入不断增大，在明确搜索方向的前提下，由全局搜索逐步转为小范围的精细搜索，以便更快地得到最优解。

2.2 基于差分进化的PID参数整定

本文将PID控制器的三个参数(比例系数KP，积分系数Ki以及微分系数Kd)以浮点数编码作为一个向量(Kp，Ki，Kd)，这个向量构成种群的一个个体。

为了将搜索范围固定在一个相对合理的空间，本文先用Ziegler-Nichols (ZN)法整定得到PID初始值，以此为中心向两头延伸，构成算法的搜索空间，提高初始搜索的成效。确定控制器参数搜索范围的不等式如下所示：

αKp*≤Kp≤βKp*，αKi*≤Ki≤βKi*，
αKd*≤Kd≤βKd*

(5)

式中:Kp*、Ki*、Kd*为ZN法的整定值;α、β为延拓系数，分别取α=0.2，β=5。

适应度函数是校核优化性能指标的关键函数，通常会采用以下三种误差积分指标：绝对误差积分指标(IAE)、平方误差积分指标(ISE)和时间加权平方误差积分指标(ITSE)。IAE指标有适当的阻尼，稳态性能好，但响应时间增加，ISE指标响应速度快，但相对稳定性差，而ITSE指标能够比较全面反映系统性能和响应时间，但其公式推导繁琐，为此提出以下较为简洁的电压综合性能指标适应度函数：

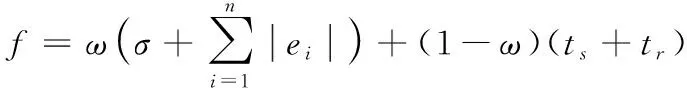
(6)

式中:ts为电压调整时间;tr为电压上升时间;ω为权重系数且ω∈[0，1];σ为电压的超调量;ei为电压输出误差。该函数综合了电压稳态性能和响应时间，ω调整二者之间的比例关系，如果侧重于电压稳态精度与超调量，需要增大ω；若侧重于电压响应时间，则可以减小ω。优化过程就是寻找一组控制参数Kp、Ki及Kd使得综合性能函数f最小化。当适应度小于设定的最小门槛，或者寻优代数达到最大，则最优解即是所求PID参数。差分迭代求取最优PID参数的步骤如图2所示。

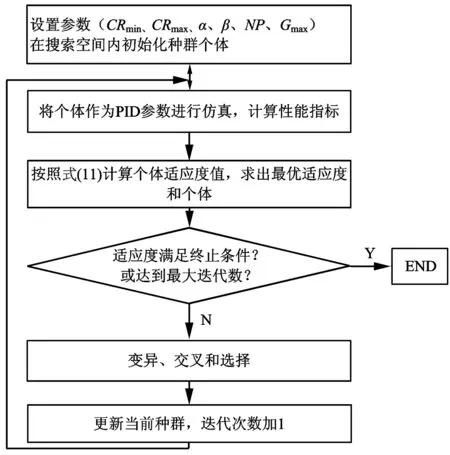
图2 励磁PID参数的差分迭代流程

3 实验验证

本文以贵州某一电厂1号机组为例，机组容量367 MVA，50 Hz，额定电压20 kV，功率因数为0.95，额定励磁电压为298 V，额定励磁电流为2 480 A，空载励磁电压为113 V，空载励磁电流为987 A。

发电机励磁参数设定如下：线路增益Kl=55，发电机增益KG=1，测量单元增益KC=1，功率放大单元增益KA=5.97；功率单元时间常数TA=0.003，电压测量时间常数Tr=0.015，发电机时间常数Td0=2。

差分进化算法参数设定如下：种群规模NP=40，总迭代次数Gmax=150，交叉算子CRmin=0.1，CRmax=0.9，缩放算子Fmax=0.9，Fmin=0.3，权重系数ω=0.7。

为了更好地验证差分进化PID控制方法的有效性，本文将粒子群优化的PID控制器与之对比，其中粒子群仿真参数设定如下：粒子种群N=50，加速算子c1=c2=2.0，标准PSO惯性权重ω=1，粒子位置Xmax=0.01，Xmin=-0.01，速度限制Vmax=0.15，Vmin=-0.15。

分别采用差分进化和粒子群优化得到的PID参数在南瑞公司的RTDS(Real Time Digital Simulators)实验装置上进行验证。RTDS是实时电力系统模拟设备，强大的运算能力可以保证电磁暂态过程的快速求解并连续实时输出，因而能够反映电力系统中的实际情形。根据电厂实际机组参数，在RTDS中构建自定义发电机励磁闭环实验系统。在RTDS系统中分别采用两种优化方法得到的PID参数，进行三相短路延迟切除、3%阶跃扰动干扰先下后上的实验。实验波形如图3和图4所示。

图3 线路三相短路延迟切除的实验结果对比

实验结果显示，基于差分进化PID的发电机励磁系统，相比于粒子群优化的PID控制系统，在受到小干扰时电压波动减小，遇到大干扰时动态降落小，恢复时间更快，动静态性能更好。

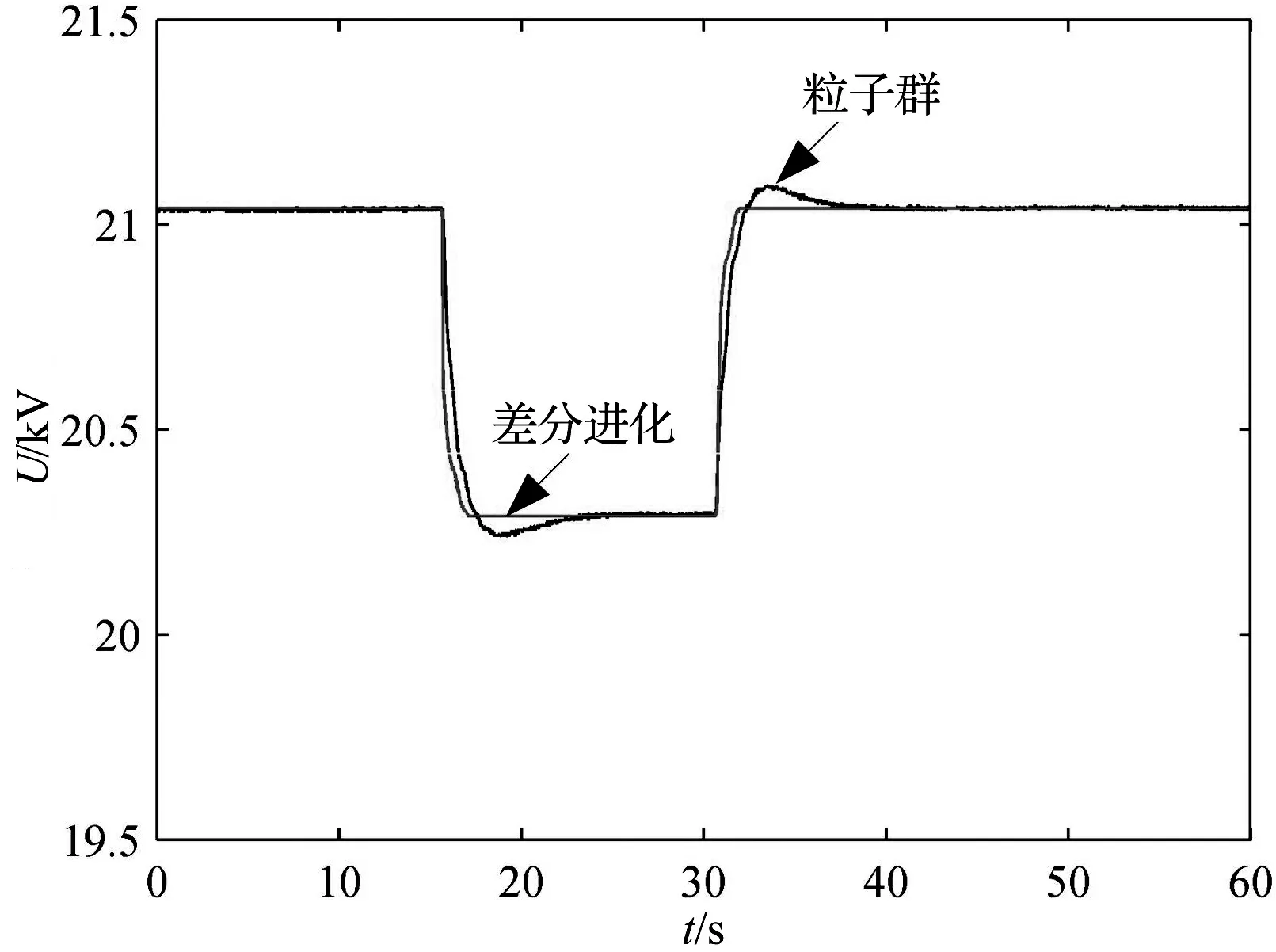
图4 系统受到3%阶跃扰动干扰先下后上的实验结果对比

4 结束语

发电机励磁控制是保证电路系统稳定的重要手段，本文分析了智能控制应用于PID励磁调节的优缺点，提出了采用差分迭代优化PID调节参数的新方法，该方法以电压控制性能综合指标为目标，对励磁系统的PID参数进行优化。差分进化算法与其他进化算法相比，收敛能力强，鲁棒性好，效率高，在此基础上将差分进化PID控制策略与粒子群PID励磁控制方法对比，并在电力系统实时模拟设备RTDS上进行实验验证，结果表明：本文所提出的方法进一步提高了励磁控制系统的稳态与动态性能，证明了本文所提出方法的正确性与有效性。