一种改进的模糊聚类算法及其应用

2018-07-31钮永莉魏光杏

长春工程学院学报（自然科学版） 2018年2期

钮永莉，魏光杏

(滁州职业技术学院信息工程系，安徽滁州 239000)

聚类分析是从已有的数据集中搜索对象之间的关系并进行分类，主要作用就是在没有先验知识的前提下，将这些对象分成聚簇的集合。模糊聚类是将模糊数学和聚类方法相结合的算法，模糊聚类方法被广泛使用在社会生活的各个领域，其中使用最多的是模糊C均值算法(FCM)。[1]但传统的FCM算法在对数据集进行分类的时候有均分的趋势，当各类样本数相差较大时，聚类结果不是太好，因此，本文对该算法进行改进，把每个样本对分类的不同作用考虑其中，且使用评价函数优化算法过程，通过实验结果表明，不管是样本均分的情况，还是样本类别差距大的情况，本算法都有更好的分类结果。

1 模糊聚类算法

模糊聚类随着模糊划分的概念首次由Ruspini教授提出，随后，Zadeh、Tarmura等学者也相继提出了基于模糊相似关系的聚类方法。基于模糊关系的聚类方法首先要建立模糊等价矩阵，当待分类的数据集比较大时，会使得计算量非常大，因此该方法现在已很少使用。取而代之的是对模糊聚类的研究，借助于神经网络、动态规划以及各类进化和遗传算法等技术，学者们提出了许多新方法，其中应用最多的就是基于目标函数的聚类方法。[2]该方法设计和实现起来都较为简单，应用范围广，随着对结果的不断优化而得到聚类结果，具有广泛的应用价值，针对不同应用环境和数据集的各种优化算法也被广泛使用。

2 模糊C均值算法

模糊C均值算法是从硬聚类算法发展而来的，即都是对目标函数的优化。把硬聚类的目标函数进行推广，充分考虑到模糊C划分要求，把每个样本与原型之间的距离用隶属度函数加权，得到了基于目标函数的模糊聚类算法，其中使用最多的是FCM算法。

模糊C均值算法首先是由美国的Bezdek教授提出的，能够实现对数据的自动聚类。其具体过程为：

假设{xi，i=1，2…n}是n个样本组成的样本集，mj，j=1，2…c为每个聚类的中心，c是类别数；μj(xi)是xi对第j类的隶属度函数，其中i表示样本，j表示类别，则聚类损失函数可以表示为:

(1)

用不同的方法定义隶属度函数并求解式(1)的极小值，就可以得到不同的模糊聚类方法。对于各个不同的聚类，模糊C均值方法要求总隶属度之和为1，即

(2)

之后令式(1)的Jf对mi和μj(xi)的偏导数为0，可得条件(3)和(4)，用迭代的方法求解这两个公式，就是基本的模糊C均值算法。

(3)

(4)

3 模糊C均值算法的改进

3.1 邻近相关度

对于所有无监督学习的聚类算法，必须考虑两个问题:一是如何确定最终分类数；二是如何把聚类的结果分配到相应的类别中。其中硬聚类HCM和模糊聚类FCM算法，使用的是最小化目标函数和误差的方法，对此有很多学者进行了研究，提出了很多解决方案。除此之外还存在一个新的问题，即FCM总是有对数据集进行均分的趋势。对数据均分趋势的问题，Bensaid等人在文献[3]一文中有详细介绍，但其算法比较复杂，所需要的计算量也大。[3]为解决该问题，本文提出了一种改进的FCM算法，综合考虑各样本点对分类的贡献率，不但能够有效提高分类精度和正确率，算法也较为简单。

对于一个数据集，如果区域内样本分布不均，甚至差异较大，则必须考虑的一个问题就是每个样本对分类的作用大小。如果某些区域样本分布密集，而其他区域样本稀疏，则聚类中心很可能在分布密集的区域。对每一个样本点来说，该点对分类的不同作用取决于其周围的样本密集度，如果周围聚集了更多的样本，则该点对分类的影响度较高。为实现该功能，本文引入一个概念：邻近相关度，用来表示某一样本点与其他样本点之间的贴近度的单调函数和。如果某样本点周围聚集有更多的点则该值较大，其对分类的影响也较大；否则值较小，表明对分类的影响也较小。

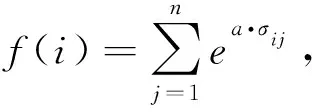
3.2 聚类有效性函数

由于FCM算法的目标函数并不考虑类与类之间的距离，为了使数据集得到最佳的分类数，我们需要一个评价函数进行迭代。本文使用如下的聚类有效性函数进行判断，保证最终分好的类是紧凑的，且类与类之间的距离尽可能远。

模糊聚类有效性函数即评估函数的定义为:S=W(c)/B(c)，其中，W(c)是类内差异，B(c)是类间差异。

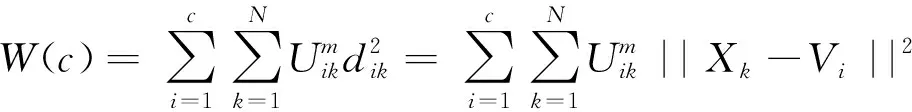
(5)

(6)

在算法执行过程中最小化S就得到了一个最有效的分类。

有研究表明，m的取值与样本数N有关，一般m的取值大于N/(N-2)，同时根据聚类有效性的迭代，可以得到m的最佳范围是[1.5，2.5]，一般取中间值m=2，模糊加权指数也为2。[4]

3.3 算法流程

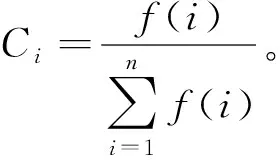
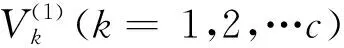
3)对t=1，2，…，Tmax，

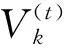
4)根据公式S=W(c)/B(c)，计算每次分类的聚类有效性函数值。

5)当聚类数目等于最低阈值(本文取m=2)时结束，否则转步骤3)，评估值最小时为最优聚类。

4 应用与实验

1)第一个实验数据来自UCI机器学习数据库的IRIS数据集，分别包含3个类四维的150个数据样本，它们分别属于鸢尾属植物的3种花的种类，每一类包含50个样本。[5]3个类中有一个类分类明显，另外两个类分类不明显，有诸多数据交叉，实验主要是检测3个类的分类效果，部分参数为a=1，c=3，m=2，ε=0.000 1，得到结果见表1。

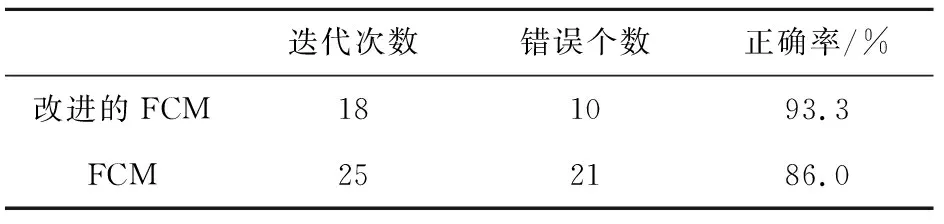
表1 IRIS数据聚类结果

2)第二组数据共有84个样本，分为3类，其中第一和第二类40个样本，第三类只有4个样本，差别较大。表2是两种方法分类的比较，p=3，a=1，c=2，m=2，ε=0.000 01，从表中可以看出，改进后的FCM算法得到了正确的分类。这是因为我们使用改进的算法对每一个样本点添加了权重(即贴近相关度)，这样较小的类由于其样本点权重值比较低就不会把自己错分到其他类中，从而取得很好的分类效果，而传统FCM算法在解决此类问题时效果欠佳。