降雨作用下蠕滑边坡渗流场与位移场的响应分析
2018-07-31杨坚
杨 坚
(肇庆市建设工程质量检测站,广东 肇庆526020)
本文基于饱和-非饱和土渗流控制理论,Geostudio软件中SLOPE/W、SEEP/W和SIGMA/W模块相耦合,对湖南湘西地区某高速公路蠕滑边坡进行降雨入渗条件下边坡的饱和-非饱和稳态、瞬态渗流场与应力场的耦合分析,从孔隙水压力、安全系数、位移时程等角度综合分析降雨强度、降雨持时、雨型等不同降雨特性对蠕滑边坡的变形破坏影响。
1 某蠕滑边坡概况
所选蠕滑边坡地处湖南湘西武陵山区,原始地貌单元属构造剥蚀山体,山间冲沟相间,地形起伏较大,边坡高程介于340~380 m,为残坡积堆积体形成的山前坡积裙。高程380 m以上为山体,自然坡度约45°,坡脚边坡坡度25°~35°,坡积裙前缘为相对较开阔的山前冲洪积平原。
根据钻孔资料,边坡体由第四系全新统残坡积堆积体和志留系中统青灰色强、中风化炭质页岩组成。上覆第四系全新统坡残积堆积体组成物质以坡残积粉质黏土为主,偶夹碎石,呈可塑~硬塑状态,无摇振反应,稍有光泽,干强度中等,韧性中等,含少量砾石,厚7~9 m。下伏志留系中统炭质页岩岩层产状40°~45°,岩层倾向与坡向平行,为顺向坡。分为强风化炭质页岩和中风化炭质页岩。地下水主要为第四系覆盖层中的孔隙水(潜水)和基岩裂隙水(潜水),其中孔隙水赋存于第四系松散覆盖层中,孔隙水稳定埋深为1.60~4.70 m。岩土体物理力学参数如表1所示。
经现场调查该边坡处于蠕滑状态,蠕滑方向基本垂直路基,后缘已产生十几米长的拉裂缝,沿坡体也出现数条拉裂缝,但该边坡尚未整体性滑动。目前,该边坡正前方为在建高速公路,一旦发生整体性失稳,将严重影响高速公路正常施工和现场施工人员的生命安全。
根据地形等高线和推测的滑动面位置,可获得该边坡主滑方向的剖面(见图1)。从现有变形情况看,在强降雨情况下,坡体前部必然出现更大变形,牵引后部坡体产生阶梯滑移,从而导致整个坡体失稳。
2 饱和-非饱和土渗流理论与稳定性分析方法
由于上覆堆积体主要成分为粉质黏土夹碎石,地下水位处于坡面下2~4 m处,地下水埋深较浅,非饱和土和饱和土中地下水的运动是相互联系的,可按饱和-非饱和土渗流问题分析强降雨条件下该边坡体的孔隙水压力响应规律及其稳定性。
2.1 饱和-非饱和渗流控制方程
2.1.1 土-水特征曲线
根据室内试验结果,选择饱和体积含水量为45%的粉质黏土的样本函数作为估算单位体积含水量函数即土-水特征曲线(见图2)。
2.1.2 饱和-非饱和渗流控制方程
可根据达西定律与质量守恒定律(连续性方程)推导出饱和-非饱和土中水渗流的控制方程:

表1 岩土体物理力学参数
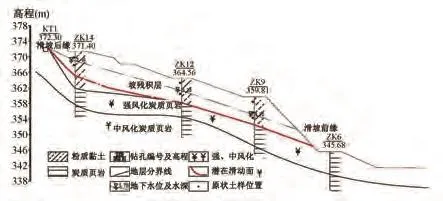
图1 边坡剖面
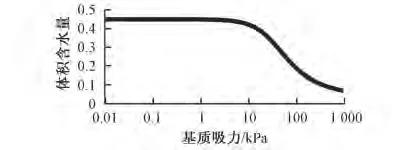
图2 粉质黏土土-水特征曲线
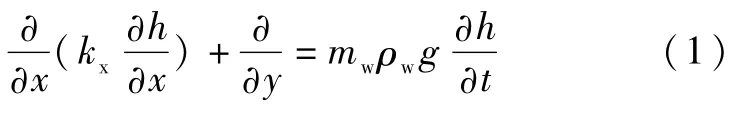
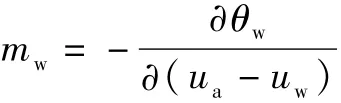
非恒定流有限元方程为:
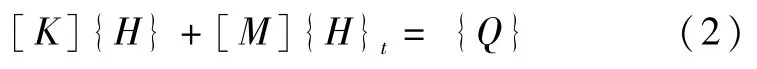
式中,[K]为单元特征矩阵;[M]为单元质量矩阵;{Q}为节点流量向量。
求解的边界条件如下:
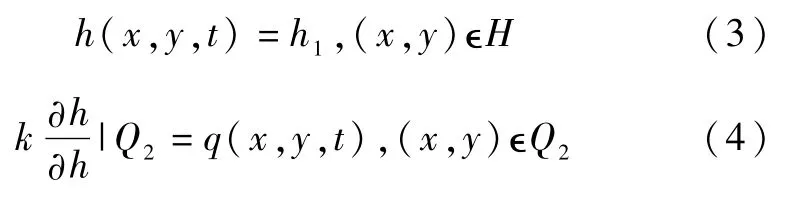
式中,H为已知水头边界;Q2为流量边界。
初始条件为:
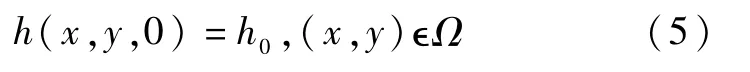
本文选用渗透系数预测模型作为粉质黏土渗透系数预测模型,其控制方程为:
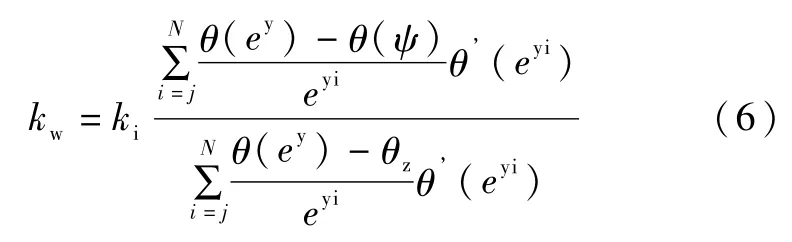
式中,kw与ks分别为计算的渗透系数函数和已测的饱和渗透系数(m/s);θ为体积含水量;e=2.718;y为虚拟积分变量,是负孔压的函数;i=j~N,介于最小、最大负孔压力;ψ对应的基质吸力插值;θ’为体积含水量的一阶导数。
根据渗透试验结果,选取粉质黏土饱和渗透系数为5.7×10-6c m/s(0.005 m/d),预测渗透系数曲线如图3所示。

图3 渗透系数预测曲线
2.2 饱和-非饱和抗剪强度理论
Fredlund等[1]在库伦饱和土抗剪强度公式基础上,提出了非饱和土抗剪强度公式,如式(7)所示。

式中,τf为抗剪强度;c’为有效黏聚力;σ为正应力;φ’为有效内摩擦角;uw为孔隙水压力;ua为孔隙气压力,实际工程中可取孔隙气压力为大气压力,即ua=0;φb为基质吸力增加引起抗剪强度增加的曲线的倾角。
2.3 稳定性分析法
基于岩土体抗剪强度参数和渗流计算结果可进行极限平衡法或有限元强度折减法的边坡稳定性计算。本文中使用瑞典条分法Morgenstern-Price法,既考虑了力平衡,又考虑了力矩平衡;在建立极限平衡方程时,同时考虑土条间的法向力和切向力,建立反映二者关系的条间力函数X=Eλf(x)。该方法适用于计算包括圆弧滑裂面在内的任意滑裂面。
3 数值模拟
3.1 建立模型
根据该边坡地质勘察报告。利用Geostudio软件中的SEEP/W模块建立有限元模型,采用四边形&三角形单元划分网格,模型中共设3个监测点,其中节点92位于边坡后缘,节点1114位于中部,节点1963位于前缘。离散后的模型、监测点及地下水位如图4所示。
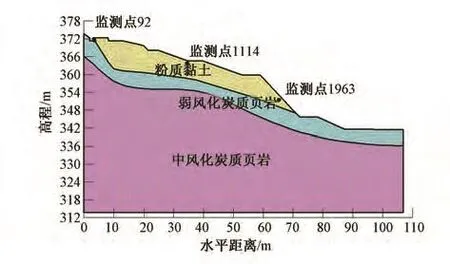
图4 模型建立与网格划分
1)边界条件 渗流边界:计算模型左、右两侧与底边为不透水边界,渗流量为0;坡面为流量边界,流量大小为降雨强度,根据相应的工况设置。应力边界:计算模型左右边界为竖直方向自由,水平方向固定;底边水平和竖直方向均固定。
2)工况设计 根据中国气象局24 h降雨强度,结合湘西地区的降雨资料,按中雨(20mm/d)、大雨(40mm/d)、暴雨(80mm/d)和大暴雨(160mm/d),设计4种降雨工况对该边坡进行数值分析。
3.2 结果分析
3.2.1 稳定降雨强度下渗流场
工况I:降雨强度为160mm/d(大暴雨),持时1,3,5,7 d。由孔隙水压力云图及渗流矢量图可知,随着强降雨进行,该边坡地下水位线逐渐上升,孔隙水压力逐渐增加,坡体非饱和区逐渐缩小,随着降雨持时的增加,局部达到饱和状态。
各监测点在降雨过程中,孔隙水压力随着降雨持时的增加而增加。位于前缘的监测点1963,在约4.3 d时孔隙水压力从负值增加到0,说明此时前缘地下水位线已经抬升到该监测点,随着降雨的持续,该点的孔隙水压力也继续增大。位于中部的监测点1114,孔隙水压力在3.0~3.6 d期间急剧增加,说明此间地下水位急剧上升,在约3.2 d时从负值增加到0,在约3.6 d后孔隙水压力随着持时的增加而缓慢增加。位于后缘的监测点92,孔隙水压力在0~0.5 d期间急剧增加,说明这期间地下水位急剧上升,约0.2 d时从负值增加到0,0.5 d以后随着降雨的持续而逐渐达到最大值,此时边坡该点处已达到饱和状态。从整体来看,孔隙水压力先快速增加后逐渐变缓(见图5),说明在边坡处于非饱和状态时,入渗速率较快,接近饱和时,雨水的入渗变得困难,这是由于渗透系数随着含水量的增加而逐渐减小的原因。

图5 监测点孔隙水压力曲线
3.2.2 不同降雨强度下孔隙水压力与变形响应
工况I I分别模拟降雨强度20mm/d持时8 d(中雨)、160mm/d持时1 d(大暴雨)的降雨过程。
从图6可知,当降雨总量为160mm时,3个监测点的孔隙水压力在不同降雨条件下的变化趋势基本一致。以监测点1963为例,持时1 d,降雨强度为160mm/d的孔隙水压力增长约2 kPa,增长速率大于降雨强度为20mm/d的孔隙水压力增长速率,最大孔隙水压力约-7 kPa。但降雨强度为20mm/d的孔隙水压力在随后的几天内持续增长,到第8 d时,孔隙水压力增大到约3.5 kPa,由负值变为正值,说明地下水位从该点以下上涨到该点以上。由此可以看出,低强度、长持时降雨,雨水能够充分渗入地下,使地下水位抬升较高,孔隙水压力增加的较多。由此可知,在降雨量相同的情况下,低强度、长持时降雨比高强度、短持时降雨对边坡的孔隙水压力影响更大。
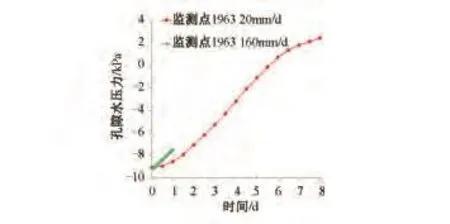
图6 监测点1963的孔隙水压力曲线
3.2.3 瞬变降雨强度下孔隙水压力与变形响应
工况III为降雨强度随时间周期性变化,即降雨从0.3 d开始,强度随时间瞬时变化,到0.45 d增加到最大值600mm/d,每日降雨量可达160mm,相当于大暴雨,之后到0.65 d再减小至0,连续7 d。
从图7可知,位于边坡中部的监测点1114处的孔隙水压力起初为负值,在降雨强度瞬时变化的前4 d,孔隙水压力持续增加,并于约第4.4d增加至0,说明地下水位随着降雨的入渗持续上升到达该监测点;之后孔隙水压力随着每天瞬时降雨强度的增大而急剧增加,之后随着降雨的结束而逐渐减小,直到下一天降雨的来临,其变化稍滞后于降雨时间,孔隙水压力总体上是增加的,说明渗流量小于降雨强度。监测点92由于位于地下水位附近,当地下水位超过该点埋深并到达地表时,该点的孔隙水压力随降雨的变化而周期性变化,变化稍滞后于降雨时间,说明此处边坡已达到饱和状态。由于雨水向下渗流,监测点1963的孔隙水压力随着降雨的变化持续增加。
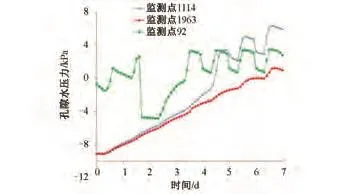
图7 监测点孔隙水压力变化曲线
由图8可知,该边坡的位移随着降雨的周期性变化而增加,边坡前端位移最大,可达33mm,向边坡上部位移逐渐变小,边坡前缘牵引中后部向下位移,由此可知,此边坡随着降雨的入渗将发生牵引式滑坡。
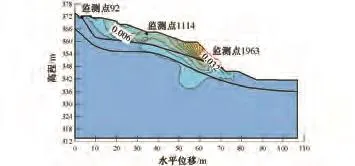
图8 降雨后边坡位移等值线与矢量图
3.2.4 强降雨后孔隙水压力响应
工况I V为降雨强度160mm/d持时1 d,分析降雨后15 d内的孔隙水压力响应与稳定性。
图9显示了降雨1 d后15 d监测点孔隙水压力变化,从中可以看出降雨强度为160mm/d持时1 d停止后,监测点1114和1963孔隙水压力随着雨水的入渗仍旧缓慢增加,直到最大值;而监测点92位于边坡最上部,雨水从上向下渗流,孔隙水压力随着降雨的结束开始减小。降雨过程中,边坡安全系数快速降低,降雨结束后,随着雨水的入渗安全系数继续降低,但降低的幅度变缓,逐渐趋于稳定。因此,降雨结束后一段时间内,边坡的孔隙水压力随着降雨的入渗继续增加直至稳定状态,安全系数则随之降低到稳定值;这说明降雨效应具有一定的滞后性,滑坡往往也发生在强降雨结束之后。
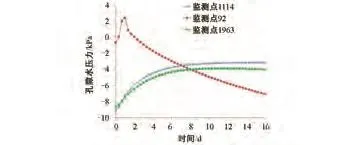
图9 监测点孔隙水压力变化曲线
4 结语
通过对湘西典型堆积层蠕滑边坡进行调查研究,分析降雨作用下蠕滑边坡的渗流场与位移场的变化,主要表现在孔隙水压力与边坡位移的变化。
1)降雨强度不变时,随着降雨持时的增加,边坡孔隙水压力增加。降雨量不变时,低强度、长持时降雨比高强度、短持时降雨对堆积层边坡的影响大,更不利于边坡的稳定。
2)降雨强度随时间瞬时变化时,边坡孔隙水压力随降雨强度的变化而变化,总体呈上升趋势,从非饱和状态逐渐变为饱和状态,安全系数随降雨强度的变化呈阶梯性降低。
3)降雨结束后一段时间内,边坡的孔隙水压力随着降雨的入渗继续增加直至稳定状态。这说明降雨效应具有一定的滞后性,往往滑坡也就发生在低强度、长持时降雨后期或结束之后,或强降雨结束之后。
4)降雨作用下该类蠕滑边坡前缘位移大于中后部位移,往往发生牵引式滑坡。
