多孔多裂纹平板的疲劳裂纹扩展试验与分析方法
2018-07-31李政鸿徐武张晓晶余音
李政鸿,徐武,张晓晶,余音
上海交通大学 航空航天学院,上海 200240
共线孔边多裂纹是飞机结构广布疲劳损伤源的一种主要形式[1-3]。试验研究表明:含共线孔边多裂纹结构的强度与寿命要比含单一裂纹结构的强度与寿命小很多[4]。飞机结构因出现共线孔边疲劳多裂纹而引起了1988年著名的Aloha航空事故[4]。为保证飞机结构安全,学术界、工程界和适航当局开展了大量研究,取得了丰富的研究成果并修订了相应的适航条款[1-3]。然而,2011年4月,美国西南航空公司一架服役了15年的Boeing 737飞机在爬升到11 000 ft (1 ft=0.304 8 m)的高度时机身快速失压。随后的事故分析表明[5]:机舱失压是由机身连接处一条1.5 m长的裂缝引起的,详细的断口分析表明这条裂缝上包含58个铆钉孔,其中54个铆钉孔的周围出现了疲劳小裂纹。这些事故和已有的研究[6-7]表明:广布疲劳损伤依然严重威胁飞机结构的安全。因此,有必要建立和完善分析飞机结构广布疲劳损伤的试验与理论分析方法,以确保飞机结构不因潜在的广布疲劳损伤而导致灾难性事故。
共线多孔多裂纹疲劳扩展寿命预测主要包括疲劳裂纹扩展分析模型和多裂纹应力强度因子分析。在疲劳裂纹扩展分析模型方面,目前主要采用的模型有Newman[8]的裂纹闭合模型和Paris疲劳裂纹扩展公式。在应力强度因子分析方面,Bowie[9]最早采用复变保角变换法给出了无限宽板孔边单裂纹的应力强度因子解。Newman[10]发展了边界元法获得了无限宽板在不同载荷情况下孔边两条等长裂纹的应力强度因子解。Fu和Zhang[11]采用复变变分法给出了有限板中心孔边两条不等长裂纹的应力强度因子解。Zhao等[12]采用复变函数法给出了无限板多孔多裂纹受远端均匀载荷作用下的应力强度因子解。郭树祥和许希武[13]采用Faber级数和保角映射技术建立了任意多孔多裂纹有限板的应力强度因子分析方法。Milliwater[14]发展了分析无限平板共线裂纹的简易方法,Chen和Wang采用积分方程法建立了有限平板共线裂纹的积分方程法[15]。最近,Xu等[7,16-18]发展了分析共线裂纹的权函数法,给出了典型共线裂纹和共线孔边裂纹的权函数和高精度应力强度因子解。对于复杂多孔多裂纹,组合法是一个常用的工程方法[19]。该方法基于已有简单裂纹问题的解析解,通过对简单裂纹问题的应力强度因子组合叠加来分析复杂裂纹,这一方法需要一定的经验,计算精度有时难以保证。有限元方法由于其适应性好,也常用于分析复杂多孔多裂纹问题的应力强度因子解[20],然而该方法在进行疲劳裂纹分析时由于计算量过大而受限制。
本文受已有工作的启发并结合作者们的前期研究基础[7,16-18],重点研究了典型多孔多裂纹平板的应力强度因子分析方法,同时设计试验研究多裂纹平板的疲劳裂纹扩展行为,并采用试验结果验证本文所提方法的有效性。初步的研究结果表明:本文的方法简单、可靠、高效,可用于多孔多裂纹结构的疲劳裂纹扩展分析和多位置损伤 (MSD)的可靠性分析。
1 疲劳裂纹扩展试验
1.1 疲劳裂纹扩展试验矩阵
本文设计了如表1和图1所示的试验矩阵。
Case 1用于获得宽范围应力强度因子变程的疲劳裂纹性能数据,以进行 Case 2~Case 6的裂纹扩展分析;Case 2用于获得单孔双裂纹的裂纹扩展行为,确定基于Paris裂纹扩展公式的寿命预测精度。Case 3~Case 6用于研究多孔多裂纹的扩展行为,验证本文的裂纹扩展分析方法。所有试样材料为2024-T3铝合金平板,厚度为1 mm, L-T取向。试样形式及切口位置分布如图1所示。试样上的缺口使用线切割慢走丝的方式切割,切割宽度为0.2 mm,方向保持水平。
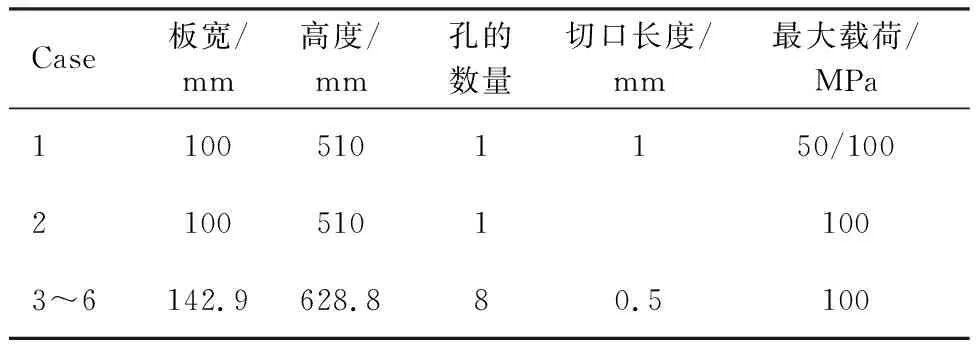
表1 试验矩阵Table 1 Test matrix
1.2 疲劳载荷
疲劳裂纹扩展试验使用MTS 10T疲劳试验机,依据ASTM标准[21],载荷加载方式为力控制,加载频率为5 Hz。为获得宽范围的疲劳裂纹扩展性能数据,本文Case 1采用了2种载荷,一个最大载荷为50 MPa,另一个最大载荷为100 MPa, 2种载荷的应力比都为0.06。每种载荷测试3个试样。其他试验的最大载荷为100 MPa,应力比为0.06。
1.3 疲劳裂纹扩展特性
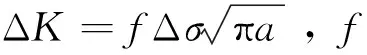
通过试验观察得到多孔多裂纹平板的疲劳裂纹扩展行为:Case 2中包含一个中心孔,孔两边无预制切口。试验过程中裂纹从孔两侧先后萌生,并向两侧水平扩展,在两侧裂纹均扩展了30~40 mm左右时,结构发生断裂;Case 3中,裂纹孔位于共线多孔的最左侧,如图1所示,其右侧裂纹首先与其右侧最接近的旁孔发生连通,之后其左侧裂纹与边界连通;Case 4中,位于中间的裂纹孔两侧裂纹以几乎相同的速率向两侧扩展,并分别与相邻旁孔连通;Case 5中,位于中间的两个裂纹孔两侧相对的两条裂纹首先发生了连通,接着最左侧的裂纹与相邻的光孔连通;Case 6中,各个孔边裂纹几乎同时扩展,在任意两条裂纹连通之前,结构发生断裂。
2 典型多孔多裂纹平板的应力强度因子分析
2.1 基于相变增韧理论的应力强度因子修正方法
本文采用相变增韧原理研究多个共线孔中旁孔对裂纹尖端应力强度因子的影响。如图3所示,一个二维任意形状(区域)的夹杂镶嵌在I型裂纹尖端应力场中,假设以裂纹尖端为原点,夹杂内任意一块积分微元的极坐标为(r,θ)。考虑夹杂对裂纹尖端应力强度因子的影响,文献[24]基于相变增韧原理和Eshelby夹杂理论给出了计算夹杂对裂纹的应力强度因子增韧值的积分表达式为
(1a)
式中:KI为无夹杂时裂尖的应力强度因子;C1和C2为与材料相关的常数,且
(1b)
其中:Ei和Em分别为夹杂和基体的弹性模量;υ为泊松比。
考虑裂纹尖端增韧作用的应力强度因子为
(2a)
(2b)
对于本文,旁孔可当作模量为0的夹杂处理,即Ei=0,代入式(1b)可得C1=C2=1。对于这种情况,式(2b)中的g为仅与裂纹及圆孔几何参数有关的系数。通过对式(2b)积分可获得不同裂纹尖端到旁孔中心距离为L时的g值。通过对积分数值的拟合,可得裂纹靠近孔边时的应力强度增韧因子g的表达式为
g(Rh/L)=
(3)
式中:Rh为孔半径;L为裂纹尖端到圆孔中心的距离。即,增韧因子只与裂纹尖端到圆孔中心的距离及孔径的比值有关。一旦孔边裂纹的应力强度因子确定,采用式(3)修正便可确定图1所示Case 3~Case 5中旁孔对裂纹尖端应力强度因子的影响。通过式(3)对无限板单孔孔边两条等长裂纹的应力强度因子进行修正便得到Case 4的应力强度因子。当Rh/L≤0.95时,式(2a)与式(3)计算的应力强度因子与有限元分析的结果相比误差在2%之内。即式(3)可高效、可靠地考虑旁孔对裂纹尖端应力强度因子的影响。
2.2 多孔多裂纹平板的应力强度因子近似解
飞机结构中,铆钉孔的孔间距w与孔直径d的比值w/d通常在4~6之间。其中孔间距w指相邻两个圆孔圆心的距离。通过计算可以得出,当孔间距在此范围内、孔边裂纹长度a与孔半径Rh的比值a/Rh≤1时,裂纹之间的相互影响很小,裂纹尖端的应力强度因子主要受裂纹孔的影响[18],这类共线多孔短裂纹的应力强度因子采用权函数法可以获得:

(4a)
(4b)
式中:G(a,x,a/Rh) 为孔边裂纹的格林函数,孔边单一裂纹和两条等长裂纹的格林函数分别由文献[25-26]给出;σ(x)为无裂纹时孔边的应力分布。当孔边出现两条不等长小裂纹时,两条裂纹的应力强度因子可分别近似采用式(4a)计算获得,其中G(a,x,a/Rh)为孔边单一裂纹的格林函数[25]。
当裂纹扩展到一定长度时,a/Rh>1,就需要考虑裂纹之间的相互影响。本文将分别给出图1中各种裂纹分布形式的具体分析方法。
对于Case 3,当a/Rh>1时,近似为有限大板孔边2条裂纹。当a/Rh>2时,把孔和裂纹等效成一条裂纹,采用文献[27]中有限大板偏心裂纹的应力强度因子,同时使用式(3)予以修正,以考虑裂纹前端孔的影响。
对于Case 4,本文采用无限单孔平板孔边两条等长裂纹的应力强度因子解,再采用式(3)修正旁孔的影响以获得裂尖的应力强度因子。
对于Case 5中的3条裂纹,当a/Rh>1时,将孔及其孔边裂纹视为一条长裂纹,如图4所示,裂纹尖端的应力强度因子采用应力强度因子手册[22]中无限平板2条不等长共线裂纹的应力强度因子解,需要注意的是在裂纹扩展分析时,只有裂尖1、2、3扩展,而裂尖4不扩展。同时,使用式(3)修正旁孔对裂尖1的影响。
对于Case 6,每个孔的初始条件一样,将其近似为周期性孔边出现2条等长裂纹。该裂纹几何的应力强度因子的计算采用式(4)的权函数法,其中周期性孔边裂纹权函数由式(5)给出,σ(x)为无裂纹时孔边应力分布[18]。
m(a,x,a/Rh,l/w,Rh/w)=G(a,x,a/Rh)·
(5)
式中:2w为孔间距;l=Rh+a。
本文将采用以上方法分析裂纹尖端的应力强度因子,进而进行疲劳裂纹扩展分析。
3 疲劳裂纹扩展分析与试验验证
由于Paris公式简单且适用于常幅谱,本文采用Paris公式及1.3节中的材料参数进行裂纹扩展分析。分析过程中所需的应力强度因子采用第2节中的方法获得。
3.1 疲劳裂纹扩展分析方法
Paris裂纹扩展公式为
(6)
对于单一裂纹或者对称裂纹,通过对式(6)进行数值积分便可以获得裂纹扩展寿命。对于多裂纹平板,由于多裂纹的协调扩展,本文按照图5所示的流程分析裂纹的扩展行为。
需要注意的是,Case 3~Case 6中初始裂纹长度定义为从预制缺口处扩展1 mm,即1.5 mm,以便减小线切割缺口对疲劳裂纹扩展分析结果的影响。而Case 2中孔边无预制切口,为方便与其他试验进行对照,在分析过程中,确定其初始裂纹长度为从孔边扩展1.5 mm。多裂纹扩展的分析流程与单一裂纹的扩展分析流程基本相同。主要区别在于,多裂纹协调扩展,各裂纹尖端的应力强度因子受其他裂纹扩展的影响。为考虑孔和裂纹间的相互影响,每个裂纹ai的应力强度因子K(ai)由第2节的分析方法给出。
采用Paris裂纹扩展公式,经过dN次疲劳循环载荷后各裂纹扩展增量为dai=C[ΔK(ai)]m·dN, 相应的裂纹长度和总循环数分别为ai=ai+dai,Ni=Ni+dN,在本文的分析中dN取100次。更新各裂纹长度,重复上述裂纹扩展分析过程,记录每个裂纹长度ai及循环次数N。
3.2 基于有限元的疲劳裂纹扩展分析方法
为验证使用第2节得到的应力强度因子解进行疲劳裂纹扩展分析的精度,评价其与基于有限元法的疲劳裂纹扩展分析相比的优劣,本文同时采用有限元法对图1所示的结构进行寿命预测。
考虑到模型的对称性,对Case 2~Case 5建立1/2对称有限元模型,对Case 6周期性孔的问题建立1/4对称模型。模型的单元类型均为平面应力4节点单元CPS4。
使用图5中的流程进行预测,与第2节分析方法不同的是,各裂纹尖端的应力强度因子通过MA-TLAB实时调用有限元软件ABAQUS计算获得。有限元模型(FEM)及Case 4的约束如图6所示,对需要设置孔边裂纹的孔周围网格进行细化,在对称面上除裂纹面以外的节点设置对称约束 YSYMM(U2=0)。其他情况的有限元模型及约束与图6类似。
3.3 疲劳裂纹扩展试验结果与分析
采用3.1节和3.2节的2种方法,分别对5种典型含孔和裂纹结构的疲劳寿命进行预测,得到了各裂纹的扩展长度和循环次数的关系。同时将2种预测结果与1.2节试验得到的数据进行对比,结果如图7所示。
在Case 2~Case 4中,以结构唯一的裂纹孔圆心为原点,Case 5以第4孔圆心为原点,Case 6以板中心为原点,在裂纹扩展方向上建立坐标系,将裂纹扩展过程中裂尖的横坐标与此时加载次数绘入图7中。图中试验寿命的起始点为扩展最快的裂纹从预制的缺口处向前扩展1 mm时的寿命,以尽量减小缺口的影响。为了与此相对应,裂纹扩展分析时,初始裂纹长度都取1.5 mm(0.5 mm的预制缺口与1 mm的裂纹扩展之和)。
对于Case 2,图7(a)给出了3个试样的疲劳裂纹扩展试验结果,由3种符号表示。本文采用有限板孔边2条等长裂纹的应力强度因子解,预测了孔边2条等长1.5 mm初始裂纹的扩展寿命,由图7(a)中的实线表示。同时,采用3.2节的有限元法预测了2条等长裂纹的扩展寿命,如图中虚线所示。由于疲劳试验分散性的原因,试验过程中会出现单边裂纹扩展很长,而另一边尚未萌生裂纹的情况。为此,本文使用有限元法预测了孔边单条1.5 mm长初始裂纹的扩展寿命,由图7(a)中点划线表示。从图中可以看出:试验结果介于单孔单边与单孔双边2种预测结果之间,有限元预测结果与采用3.1节方法的计算结果基本一致。
图7(b)给出了Case 3的试验结果和分析预测得到的裂纹扩展长度与循环次数的关系。采用本文提出的近似方法预测了孔边两侧出现1.5 mm等长初始裂纹的扩展情况,并由实线表示。采用有限元法的预测结果由图中虚线表示。从图中可以看出,采用本文近似应力强度因子解预测的裂纹扩展与采用有限法计算的结果基本一致。
图7(c) 给出了Case 4的试验结果和分析预测裂纹扩展长度与循环次数的关系。对比试验结果表明:Case 3孔边裂纹连通旁孔的寿命要比Case 4连通旁孔的寿命短。这表明,试样最外侧孔出现孔边裂纹更危险。从图中可以看出:基于有限元和本文第2节的应力强度因子解都可以可靠地预测裂纹的扩展。
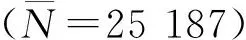

从图7的结果可以看出,分析预测的裂纹扩展行为及连通顺序与试验结果一致。使用简单、近似的应力强度因子方法与使用有限元法进行寿命预测的结果相差很小。相比于有限元法,本文给出的方法更加简单、高效。
4 结 论
通过试验、理论和有限元分析,研究了2024-T3铝合金单孔孔边裂纹及典型多孔多裂纹平板的应力强度因子解和疲劳裂纹扩展行为,得到以下结论:
1) 多裂纹明显降低了结构疲劳裂纹扩展寿命。就本文研究的典型多孔多裂纹板及载荷条件,所有共线孔都出现等长裂纹的这一极端情况,其疲劳裂纹扩展寿命是单孔双裂纹平板疲劳裂纹扩展寿命的10%左右。这表明飞机结构广布疲劳损伤严重威胁飞机结构安全。
2) 结合相变增韧原理和权函数方法给出了4种典型的多孔多裂纹平板的裂尖应力强度因子解,这些解可定量考虑孔的影响及裂纹之间的影响。采用这些简易的应力强度因子解进行疲劳裂纹扩展分析的结果与采用有限元法分析的结果基本一致,且预测的疲劳裂纹扩展寿命与试验结果吻合良好。相比于有限元法,本文给出的应力强度因子分析方法更加简单、高效。
