一种基于动态补偿技术的微小稳态推力还原方法
2018-07-31周伟静洪延姬叶继飞李南雷常浩
周伟静,洪延姬,叶继飞,李南雷,常浩
航天工程大学 激光推进及其应用国家重点实验室,北京 101416
微纳卫星具有重量轻、性能好、开发成本低、周期短、功耗低等特点,目前已经成为中型、大型等传统卫星的有效补充,并带来了全新的应用模式和应用理念。微纳卫星的全面发展推动了微推力器的快速发展,冷气微推力器[1]、脉冲等离子体微推力器[1]、场发射电推进[1]、胶体微推力器[1]、MEMS(Micro-Electro-Mechanical Systems)阵列[2]、激光烧蚀微推力器[3]、微波微推力器[4-5]等新型微推力器应运而生。
随着这些微推力器的设计、研制和应用,微推力测量技术亦备受关注[6-7]。微推力测量一般分为稳态推力测量[8-11]、脉冲平均推力[9-10]和脉冲冲量测量[9-10,12-14],稳态推力范围一般在几百微牛至几十毫牛,脉冲冲量范围一般在几十微牛秒至几百微牛秒。稳态推力测量和脉冲冲量测量均采用直接测量方法,即将推力器与推力测量装置固连,利用推力的反冲作用,将推力转化为推力测量装置的力学行为,如振动幅值或转动位移,测量振幅或位移等信息可获得推力或冲量大小。目前,水平旋转的扭摆是最适宜测量微小推力或冲量的测量装置。
对于脉冲式微推力器,脉冲冲量测量的实现相对简单,只要力的作用时间小于欠阻尼扭摆测量系统振动周期的1/4[15],可以看做脉冲力瞬间作用于扭摆,根据扭摆响应的最大幅值即可计算脉冲冲量。对于稳态微推力器或高频多脉冲微推力器(输出等同于稳态推力),只要力或多脉冲的作用时间大于欠阻尼扭摆系统允许误差范围的调整时间,并且维持稳态一定时间,就可以根据扭摆响应的稳态幅值计算稳态推力大小[16]。
在机理研究阶段和设计研制过程中,微推力器的推进性能需要测试跟踪,以形成研究闭环,不断改进和提升推进性能。目前,微推力器的研制多处于原理样机或初样机阶段。脉冲式微推力器的单脉冲冲量测量容易实现。但是,由于携带推进剂受限(如激光烧蚀微推力器)、频率控制受限(阴极微弧微推力器)、功率受限(如微波推力器)等原因,单次实验条件下,稳态或多脉冲微推力器开机时长较短,在扭摆响应达到调整时间之前就需关机[17],无法根据稳态响应还原稳态推力。
通过增大阻尼比和固有频率,可以减小扭摆系统的调整时间,使扭摆响应能尽快进入稳态。但是,一方面,为了能够高精度地标定测量系统的系统参数,阻尼比最好在[0.1,0.4]范围内;另一方面,微推力器的推重比较小,在承载较大质量推力器的基础上,要能够辨识微牛量级的推力,测量系统振动频率均小于1 Hz。因此,通过增大阻尼比和固有频率的方法,很难从根本上解决减小调整时间的问题,而且在实验操作时,需要多次调节阻尼比和转动惯量,并多次测试后方可达到测量要求,实施繁琐,周期长。
本文针对微推力器开机工作时间与测量系统调整时间的匹配难题,提出了一种基于动态补偿技术的微小稳态推力测量还原方法,利用动态补偿技术改变测量系统的调整时间,并提出了一种补偿器设计原则,通过实验验证了该方法的有效性。利用该方法可以从根本上缩短调整时间,不需要从硬件上做出修改,大大缩短实验时间,并且具有很强的通用性。
1 基于水平扭摆的微小稳态推力测量
水平扭摆基本结构如图1所示。扭摆横梁一端安装推力器,另一端安装配重,使得横梁本身、推力器和配重的重心位于转轴上。水平扭摆是二阶质量-弹簧-阻尼系统,其基本运动方程为
(1)
式中:θ为扭摆横梁相对于横梁零点的转角;J为测量系统转动部件(包括横梁、推力器和配重)相对于转轴的转动惯量;ζ为阻尼比;ωn为无阻尼自振角频率;f(t)为推力器推力;b为推力器推力作用力臂。
因推力器输出的稳态力上升时间非常快,可以当做阶跃力处理,即f(t)=F,则扭摆系统在阶跃力作用下,系统响应为
(2)
(3)
式中:k为测量系统的扭转刚度系数。
扭摆系统的典型响应如图2所示。ts为扭摆的调整时间,t0为扭摆的1/4振动周期时刻。当稳态力作用时间Tf=t2,且稳态转角采样区间[ts,t2]大于振动周期的0.2倍时,就可以利用采样区间内的稳态转角均值计算稳态推力,且这种平均法带来的相对误差可以控制在一定水平,后文将详细分析。但是当稳态力作用时间Tf=t1>t0,系统响应还没达到稳态,此时无法利用稳态响应值计算推力。文献[18]给出了一种基于杜哈梅积分法实时计算微推力的方法,但该方法的精度取决于采样频率和噪声,且真值的收敛速度取决于测量系统的固有频率。因此,本文提出利用动态补偿技术改变测量系统的动态特性,减小测量系统的调整时间。
2 动态补偿技术
2.1 动态补偿基本原理
动态补偿的原理[19]是:在原测试系统传递函数上增加一个补偿环节,使得总的传递函数达到理想状态,从而达到改善系统动态特性的目的。补偿环节以辨识建模得到的模型为依据,设计出一种动态补偿滤波器,与原来的测试系统相串联,使级联补偿器后系统总的动态性能满足使用要求。根据扭摆测量系统特点,基于动态补偿技术的推力测量方案如图3所示。
首先,将标定力加载到测量系统上,根据测量系统在标定力下的响应,进行系统动态模型辨识;然后,根据系统动态模型设计动态补偿滤波器;最后,将推力器推力加载到测量系统上,将测量系统在推力作用下的响应,经过动态补偿滤波器,还原出推力大小。
动态模型辨识的方法较多[19],这里不予赘述。本文采用的动态模型辨识方法的基本思路为:首先,根据模型阶次估计准则,利用同时辨识模型阶次和参数的方法确定模型阶次;其次,根据输入输出数据,利用最小二乘法估计模型参数以作为迭代初值;最后,利用特殊白化滤波器的广义最小二乘法估计模型参数。
图3所示的测量过程中,动态补偿滤波器是关键,进行软件补偿即可。常采用的设计方法有直接选择等效系统法和零极点配置法,还有众多研究人员提出了粒子群算法、神经网络等复杂的补偿器设计方法。本文所涉及的微推力测量系统属于低阶系统,考虑采用基于直接选择等效系统法的动态补偿滤波器设计方法。
2.2 动态补偿滤波器设计
直接选择等效系统法设计动态补偿数字滤波器的基本思想是:根据系统动态标定的瞬态响应曲线,由经典控制理论知识,直接得到描述系统特性的动态数学模型,对其模型进行动态分析,当其动态特性不满足测量要求时,给系统串联一个动态补偿数字滤波器,使得串联后构成的等效系统能够满足测量系统的动态特性。
取fr=kθ/b,则式(1)可改写成
(4)
测量系统传递函数为
(5)
式(5)可串连一个阻尼比与固有频率均相同的二阶微分环节,为了减少高频干扰,同样可以加上一个二阶低通滤波器,即将动态补偿滤波器设计成具有下述传递函数的形式:
(6)
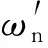
动态补偿滤波器与测量系统串联后的等效系统传递函数为
(7)
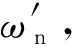
3 扭摆稳态响应测量的动态补偿器设计分析
3.1 扭摆稳态响应与稳态推力测量的关系
根据式(2),设在时间区间[T0,T1]内,扭摆系统在阶跃推力作用下的响应均值为
(8)

利用稳态转角均值计算稳态转角的相对误差为
|e-ζωnT1sin(ωdT1+2α)-e-ζωnT0·
(9)
设T0=k02π/ωd(k0为T0的周期倍数因子),T1=k12π/ωd(k1为T1的周期倍数因子),且ωd(T1-T0)≥x1≥1,ζωnT0≥x2≫1时,式(9)变为
(10)

根据上述分析,当x1≥10和x2≥5,扭摆系统阻尼比不同时,采样区间和相对误差如表1所示。由表1可以看出,具有一定阻尼比的扭摆系统在推力作用下,只要进入稳态的时间区间至少能覆盖某一区间[ts1,ts2],就可以将稳态转角均值代替稳态扭转角时的相对误差控制在可忽略的水平。
表1不同阻尼比下的采样区间和相对误差
Table1Samplingrangesandrelativeerrorsfordifferentdampingratios

ζ采样区间[ts1,ts2]δ/%0.2[3.898 5T,5.49T]≤0.076 10.3[2.530 4T,4.122T]≤0.070 30.4[1.823 3T,3.414 9T]≤0.068 20.5[1.378 3T,2.969 9T]≤0.067 60.6[1.061T,2.652 6T]≤0.067 40.7[0.811 9T,2.403 4T]≤0.067 4
3.2 动态补偿器设计原则
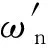
(11)
3.3 动态补偿下的稳态推力还原步骤
综上所述,当推力实际工作时间大于扭摆系统周期的0.25倍,且小于扭摆系统调整时间时,可通过动态补偿方法建立新的等效测量系统,使得推力作用在等效测量系统上时,能够利用稳态响应均值计算推力大小。由2.2节和3.1节可知,根据补偿后输出的均值计算稳态力的误差主要来自3个方面:
1) 补偿器输入fr存在的误差
由fr=kθ/b可知,fr的误差来源于θ、k和b,根据文献[20]可知,由于环境等干扰会产生测量噪声,造成实际系统响应数据在平均位置曲线附近上下波动,可采用正交多项式局部滑动拟合方法,对实际系统响应测量值进行平滑降噪处理,确定系统响应的平均位置曲线。刚度系数k为具有置信区间的标定值,b存在误差区间的测量力臂值。因此,fr的误差可认为来自于k和b,且k越大、b越小,fr越大。
2) 补偿器Hd(s)中系统参数ζ和ωn带来的误差
系统参数ζ和ωn均为原始测量系统具有置信区间的标定值。其中,ζ主要影响Hd(s)系统稳定的快速性,不影响稳态响应。因此,仅考虑系统参数ωn对补偿器稳态输出的影响,且ωn越大,稳态响应越大。
3) 补偿后输出在[0.811 9T′,2.403 4T′]区间内取均值带来的误差
根据3.1节的结论,在阻尼比为0.7的条件下,在[0.811 9T′,2.403 4T′]区间内取均值,利用稳态转角均值代替稳态扭转角时的相对误差≤0.067 4%,该误差可以忽略。
综合上述分析,提出动态补偿下的稳态推力还原步骤如下:
步骤1标定扭摆测量系统的系统参数[21],获取扭摆测量系统参数及其置信区间ζ±Δζ、ωn±Δωn、T±ΔT、k±Δk,判断测量系统的调整时间ts。
步骤2如果稳态力作用时间0.25T≤Tf≤ts,进入步骤3,否则直接根据扭摆响应的稳态幅值计算稳态推力大小。
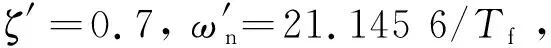
4 稳态推力还原的实验分析
利用文献[22]中构建的水平扭摆测量系统进行实验验证,该测量系统由水平面调节机构、水平扭转机构、位移测量装置、电磁标定装置和阻尼装置组成。水平面调节机构用于提供整个测量机构的安装底座支撑以及参考水平面。水平扭转机构的主要机构是水平横梁,用于安装推力器。水平面调节机构和水平扭转机构之间利用无摩擦枢轴连接,从而推力器工作时水平横梁能够在水平面内发生转动。位移测量装置用于测量水平横梁的位移,在扭转角小于5°时,可以利用水平横梁的位移量代替扭转角度。电磁标定装置为非接触电磁力产生装置,由永磁铁部分和线圈部分组成,永磁铁部分安装在水平横梁上,线圈安装在固定底座上,当线圈通特定电流时,即可产生电磁力使水平横梁发生转动,标定装置的电磁力采用电子天平计量,作为测量系统的标定源。阻尼装置用于提供测量系统的阻尼。对该测量系统的弹性轴、标定力装置和位移测量装置进行了调整,量程扩展到10 mN,放置在真空模拟环境中的测量系统如图5所示。
首先对测量系统进行标定。真空度为3.1×10-4Pa,真空舱内温度为20 ℃,位移传感器采样频率为520.8 Hz,电磁阻尼电流设置为0.4 A。对扭摆测量系统分别加载和卸载0.139、0.283、0.601、0.890、1.179 mN的电磁力,电磁力作用力臂为0.5 m,传感器测量力臂为0.59 m,测量系统响应如图6所示。由于真空系统振动的影响,从局部放大图图7可以看出,测量系统响应存在高频噪声,由频谱分析可知,噪声集中在47 Hz和 35 Hz。对数据进行滤波处理后,根据文献[21]的处理方法,可得扭摆系统的系统参数及95%置信区间如表2所示。
在测量系统标定后,利用标定力模拟实际推力器输出的稳态力,设定标定力幅值为500.469 μN,控制稳态力工作时间分别为3、10、20 s。按3.3节的步骤,设计了相应的补偿滤波器,取均值获取了相应的推力大小,测量系统的实际响应(取的是位移的相对值)以及补偿后的输出如图8所示(图8中相关参数的取值为k=0.381 38 N·m/rad、b=0.5 m、ωn=0.783 63 rad/s)。根据3.3节的步骤,获得的推力大小范围及与输入的偏差如表3所示。

表2 系统参数及95%置信区间Table 2 System parameters and 95% confidence interval

输入推力/μN工作时间/s系统周期倍数补偿后输出/μN相对误差/%500.46930.365 4[492.313 5,508.101 2][-1.63,1.53]500.469101.218 1[492.441 7,506.817 1][-1.6,1.27]500.469202.436 2[492.225 8,507.952 4][-1.65,1.5]
由图8(a)可以看出,在稳态力作用下,由于力作用时间以及测量系统的特点,测量系统均未达到稳定状态,无法利用扭摆的稳态位置相对变化量换算推力。由图8(b)可以看出,利用动态补偿技术后,等效系统最终的输出能够很快达到稳定状态,并利用稳态平均值还原出推力大小。从表3可以看出,根据本文步骤能够给出还原推力大小范围,且与输入的偏差能保证在2%以内。因此,当稳态推力实际工作时间大于扭摆系统周期的0.25倍,且小于扭摆系统调整时间时,可以利用本文提出的补偿方法还原出稳态推力大小。
5 结 论
新型微推力器的力学性能测量对推力器的工作机理、设计和应用都具有很强的工程价值。由于新型推力器研究和设计阶段的特殊性,有时推力器稳态推力输出时间较短,与机械式测量装置的稳态调整时间匹配困难,无法利用稳态推力与测量系统稳态响应成线性关系这一原理还原推力大小。本文提出一种基于动态补偿技术的方法,详细分析了扭摆稳态响应与稳态推力测量的关系,提出了补偿器的设计原则,总结了推力还原步骤,并通过实验验证了该方法的有效性。具体研究结论如下:
1) 稳态推力长时间作用在水平扭摆式微小推力测量系统时,系统响应会进入稳态,如果在稳态响应某一区间内采样稳态转角值,可以利用稳态转角均值代替稳态扭转角,从而通过稳态扭转角与稳态推力的线性关系计算稳态推力大小,而且这种计算方法带来的相对误差不超过0.1%。
2) 实验结果表明,当推力实际工作时间大于扭摆系统周期的0.25倍,且小于扭摆系统调整时间时,可利用本文提出的基于动态补偿技术的微小推力还原方法,建立新的等效测量系统,使得推力作用在等效测量系统上时,能够利用稳态响应均值计算推力范围。
3) 基于动态补偿技术的微小推力还原方法适用于推力实际工作时间大于扭摆系统周期的0.25倍,且小于扭摆系统调整时间的情况。所以,一方面在设计测量系统时,在兼顾量程等指标的前提条件下,尽量使得扭摆系统的周期小;另一方面采用动态补偿方法还原推力不需要修改硬件或进行复杂的硬件调整,适用于类似水平扭摆的二阶测量系统,具有很强的通用性。
