叶片式涡流发生器对压缩拐角流动分离的控制
2018-07-31胡万林于剑刘宏康赵渊阎超
胡万林,于剑,刘宏康,赵渊,阎超
北京航空航天大学 航空科学与工程学院,北京 100083
在超声速飞行器的内外流动中普遍存在着流动分离的现象,包括激波诱导的边界层分离、绕流引起的分离、尾迹区的分离等[1]。激波诱导的边界层分离会造成较大的能量损失,增大阻力,并伴随有非定常效应[2]。对飞行器的稳定性和操控性带来影响,特殊区域的流动分离再附还会引起严峻的局部气动加热现象,对飞行器造成一定的危害。因此,对流动分离进行有效控制就具有非常实际的工程意义。
涡流发生器作为一种被动控制技术,将动量从外部高速流输运到边界层内,加强边界层低速区的能量,增强边界层抵抗逆压梯度的能力[3]。按其尺寸可分为传统涡流发生器(VGs,其高度h与边界层的厚度δ之比h/δ~1)和微型涡流发生器(MVGs,h/δ在0.1~0.5之间,又被称为低形阻涡流发生器[4]),因其结构简单和经济性而被广泛研究。1947年,Taylor[5]首次提出了涡流发生器的概念,随后被广泛应用于航空领域,延迟边界层分离[6],提升机翼的升阻力特性[7-10],降低机体后的阻力[11]等。Brown等[12]于1967年,研究了涡流发生器对于亚声速扩压管边界层分离的控制效果,发现用特制的涡流发生器能减小压力损失并使得流场均匀。然而传统的涡流发生器形阻较大,其实用性为人所质疑。微涡流发生器于20世纪70年代开始为人们所研究,Kuethe[13]用波浪形的微型涡流发生器控制尾迹区的流动,减小了其声学上的扰动。Ashill等[14]于2001年结合试验与理论研究了微型涡流发生器尾迹区的流动结构,并应用于跨声速机翼的流动,达到了增升减阻的目的。Anderson等[15]于2006年对微三角楔的形状进行优化研究,提出了一套优化尺寸。基于Ashill、Anderson等的微三角楔形涡流发生器,张庆虎[1]于2013年试验研究了这两种涡流发生器对于4种边界层分离的控制效果,精细显示了其流场结构,并分析其时间演化特性。2016年Schreyer等[16]用试验和大涡模拟(LES)数值方法研究了微斜楔涡流发生器诱导的流向涡对于压缩拐角分离区的激波边界层干扰的影响。
近年来,微型涡流发生器以其低形阻、经济等特性,成为众多科研工作者们研究的热点[17-18]。虽然前人对于涡流发生器的相关研究较为充分,其应用也逐步成熟,然而,有关利用叶片式涡流发生器控制压缩拐角处的边界层分离方面的研究较少,其控制机制与性能尚不明确。因此,本文运用数值模拟的方法研究超声速压缩拐角引起的激波边界层干扰现象,并分析梯形叶片式涡流发生器的几何参数对其控制效果的影响。
1 物理模型
叶片式涡流发生器放置位置如图1所示,其后缘距平板前缘400 mm,距拐角处100 mm,无控制时当地边界层厚度δ=7.5 mm。其摆放方式,主要分为相向旋转(Counter-rotating,Ct)和同向旋转(Co-rotating,Co),如图2和图3所示。各涡流发生器的几何参数见表1,尺寸标注如图4所示。表1中Ct1~Ct7为相向旋转计算实例,Co1为同向旋转计算实例。涡流发生器后缘高度为h,底边长度为e,叶片厚度为d,前缘后掠角度β=30°,涡流发生器与来流方向夹角α=23°,相向旋转时角度相反,同向旋转叶片后缘间距为λ,相向旋转叶片后缘间距为η,沿展向布置叶片的对数为n,沿展向布置多个涡流发生器用于模拟叶片间的相互作用。
图5为涡流发生器局部壁面及对称面网格。采用多块对接结构网格,网格总量在1 000~2 500万之间。入口、出口及顶部为远场边界,两侧面为对称边界。
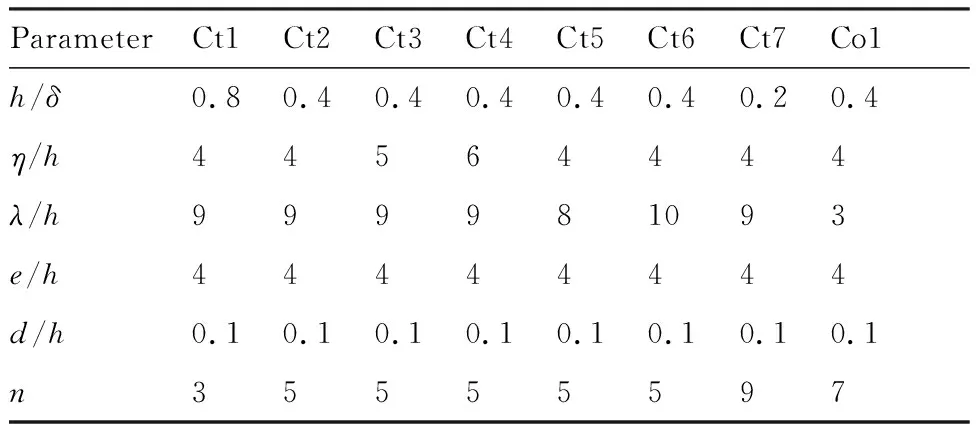
ParameterCt1Ct2Ct3Ct4Ct5Ct6Ct7Co1h/δ0.80.40.40.40.40.40.20.4η/h44564444λ/h999981093e/h44444444d/h0.10.10.10.10.10.10.10.1n35555597
2 湍流模型验证
本文采用定常状态计算,模拟涡流发生器对24°压缩拐角边界层分离的流动控制作用。本质上,带有叶片式涡流发生器的压缩拐角的流动是非定常的,但是模拟叶片式涡流发生器几何参数对于其控制作用的影响,侧重于反应宏观上的统计规律,利用定常的雷诺平均Navier-Stokes(RANS)方法是合适的。基于本文CFD求解器,赵瑞和阎超[19]分别采用了Spalart-Allmaras(S-A)湍流模型、k-ω两方程模型、Shear Stress Transport(SST)湍流模型对超声速压缩拐角进行了数值模拟,并与试验[20]对比。结果表明,对于24°压缩拐角,S-A与SST模型分离区物面压力预测结果偏大,而k-ω计算结果偏小,S-A与SST模型预测分离点提前,再附点滞后,分离区过大,而k-ω模型虽然预测分离点与再附点均稍有滞后,但预测的分离区大小较为准确,对于本文的研究较合适。本文数值模拟的来流条件见表2,表中Ma∞、p∞、T∞分别为来流参数马赫数、密度、压力和温度,Re为单位雷诺数。

表2 来流条件Table 2 Freestream conditions
3 相向旋转叶片式涡流发生器的控制效果
3.1 空间流动结构
图 6为安装h=0.4δ的相向旋转式VGs后,壁面压力(p)分布及其空间流线(马赫数Ma着色)。气流流过VGs叶片后,卷起一对方向相反的流向涡,增大了主流与边界层的动量输运;在相邻两对VGs中间处,气流平直流过,并未有分离涡产生。
图 7给出了不同站位处(x-x1=h、5h、10h、15h,x为流向坐标,x1为VGs后缘处的坐标)流向无量纲涡量(ωxh/u0,ωx为x方向的涡量,u0为来流速度)分布,图中实线为流线,虚线为无控制时当地边界层所在位置。在VGs后流向涡强度逐渐衰减,但涡核位置贴近壁面,在法向上并未有明显上升,流向涡主要在边界层内,对主流的影响不大。
本文求流向涡环量采用Q准则[21],如式(1)所示,提取Q=0时的轮廓线作为涡核区域的边界,并沿边界进行曲线积分求得环量Г,如式(2)所示,用来流速度u0和VGs后缘高度h进行无量纲化。
(1)
(2)
式中:Ω和S分别为速度梯度的反对称与对称张量;Г为环量大小;u、v、w分别为x、y、z方向的速度;l为旋涡边界曲线。
图 8给出了无控制和有控制时壁面摩擦力系数(Cf)分布云图,无控制时上游分离点及下游再附点距转折处长度分别为Ls=19.10 mm和Lr=11.07 mm。安装0.4δ高度的MVGs后,在其尾部分离再附区显著减小,而在相邻两对MVGs中的尾部分离再附区反而有所增加,为综合考量VGs对于边界层分离的控制作用,求分离区长度的平均值可得Ls=14.47 mm、Lr=3.73 mm,对比无控制的结果,Ls约减小24.24%,Lr约减小66.31%,总长度L约减小了39.68%。文中有控制时所述分离区长度均指平均长度。
3.2 壁面压力分布曲线及速度型曲线
图 9给出了无控制时压缩拐角对称面处及安装相向旋转VGs后特征位置处(相向旋转叶片中心线A、叶片后缘B、相邻两对叶片中心线C)壁面无量纲压力分布,图中x0为拐角处坐标。可看出,无控制时(对应图中Clean),斜坡产生的高压力通过边界层传递到上游,使得在拐角前压力有所升高。安装VGs后,减弱了转角处的分离,使得在转折点前壁面压力缓慢增大,在转折点附近较原始压力低,在转折点后,B、C处壁面压力恢复到未安装VGs之前的压力值,而A处由于流向涡的再附使得壁面压力明显增大。
图10给出了x=-4δ(分离区前)截面处沿壁面法向(y方向)的速度型曲线。可看出,过A处的速度型最饱满,在y<0.5δ时,边界层内的速度大于无控制时的速度;过B处及C处的速度型曲线不及无控制时饱满,过B处,在y很小时,边界层内的速度略大于无控制时的速度,而过C处,边界层内存在着回流。
3.3 对分离区流动结构的控制效果
4 涡流发生器几何参数的影响
图12给出了无控制和有控制时分离再附区无量纲平均长度(L/δ)的柱状图。无控制时分离区长度L约为3.9δ,其中Ls约为2.5δ,Lr约为1.4δ。计算结果表明,各涡流发生器均能控制压缩拐角处的分离区,且Lr减小幅度更大。图 13给出了无控制和有控制时阻力系数(CD)的大小,安装VGs后系统的阻力均有些许增大。
图 14给出了各不同参数影响下的壁面无量纲压力分布以及不同流向位置处(x-x1=h、5h、10h、15h、20h)的无量纲环量大小,R1、R2分别表示中心线一侧第1个和第2个涡旋。对于壁面压力分布,不同几何参数的影响主要体现于分离区内。对于各叶片尾迹区无量纲环量分布,其规律与Hunt等[22]结论相似,沿流向逐渐减小,且趋于平缓。
对比不同摆放方式的VGs (Ct2、Co1)的控制效果。图12表明,对于两种摆放方式的VGs,分离再附区总长度L相当,但同向旋转方式,分离点距转折点的距离Ls较小,可知同向旋转方式的VGs利于减小Ls的大小,相向旋转方式的VGs利于减小Lr的大小。同时,图13表明同向旋转方式的系统阻力更小。对比壁面压力分布规律,在转折点前,同向旋转VGs壁面压力略低于相向旋转VGs,改善了分离区的压力分布。过中心线A处,相向旋转VGs的壁面压力出现一个峰值,而同向旋转的VGs壁面压力则缓慢增大无明显峰值。对比其尾迹区流向涡环量的大小,相向旋转的VGs,各叶片后涡强度相当,而同向旋转叶片R1处比R2处略小,在远离VGs的后方差值越大,且同向旋转叶片环量较相向旋转的略大,如图 14(a)所示。
对比不同高度(h)VGs (Ct1、Ct2和Ct7)的控制效果。图 12表明,h越大Ls、Lr减小幅度均越大。图13表明,系统的阻力在h=0.4δ时最小,h=0.2δ较h=0.4δ系统阻力增大的更多,经分析认为可能是所用VGs的数目更多所致。在分离区内,较高的VGs能有效减小边界层内压力的前传,h=0.8δ时,在拐角下游过中心线A处壁面压力的峰值越高,而h=0.2δ时,过中心线A、C处壁面压力分布相当且无明显峰值出现。流向涡无量纲环量也随着h的增大而增大,相较其他因素其幅度变化也最大,如图 14(b)所示。
对比不同相向旋转叶片间距(η)VGs (Ct2、Ct3和Ct4) 的控制效果。图12表明,η越大Ls减小幅度越大,Lr减小幅度反而越小,总长度L减小幅度越大。控制效果较好的是η=6h,Ls减小了42.04%,Lr减小了65.49%,L减小了50.65%。图13表明,系统阻力随η的增大而增大。增大η,壁面压力在转折点前略减小,转折点后略增大,减小了边界层内压力的前传,改善了分离区的压力分布,同时流向涡无量纲环量也随之增大,η=6h时,Г增幅略大,原因可能是减小了流向涡对间的干扰,如图 14(c)所示。
对比不同同向旋转叶片间距(λ)的VGs (Ct2、Ct5和Ct6)的控制效果。图 12表明,λ越大,Ls和Lr减小幅度均越小。控制效果较好的VGs排列是λ=8h,Ls减小率可达43.04%,Lr减小率可达70.55%,总长度减小了53.13%。图13表明,系统阻力随λ的增大而减小。增大λ,壁面压力在转折点前略增大,转折点后略减小,不利于改善分离区的压力分布,同时流向涡无量纲环量也随之减小,但减幅不明显,如图 14(d)所示。
5 结 论
本文采用数值模拟的方法,研究了梯形叶片式涡流发生器对超声速压缩拐角边界层分离控制的效果。从分离区平均长度和系统阻力的变化着手,结合壁面压力分布及流向涡环量的大小,客观评价了涡流发生器的摆放方式及叶片的几何参数对于边界层分离控制效果的影响规律,结论如下:
1) 叶片式涡流发生器将转角处的二维分离转变为三维的分离流动,降低了分离区内壁面压力,同时减小了分离区长度。
2) 在上游叶片式涡流发生器作用下,流向涡是直接影响拐角处边界层分离的原因,流向涡强度越大控制效果越好。高度对叶片式涡流发生器诱发的流向涡强度起主要作用,异向与同向叶片间距的影响较小。
3) 相对于相向旋转方式,同向旋转叶片式涡流发生器减小了边界层内压力的前传,更利于改善分离区内的压力分布,分离区总长度的减小量与相向旋转方式相当,但分离点距转折处平均长度更短。系统的阻力增量也较相向旋转方式的小。
4) 对于相向旋转叶片式涡流发生器,后缘高度越高,分离区长度越小,后缘高度h=0.4δ时系统阻力增量最小;相向旋转叶片间距越大,分离区总长度越小,系统阻力增量越大;同向旋转叶片间距越大,分离区总长度越大,系统阻力增量越小。
