楔型螺纹螺母可靠性初步评估方法研究

，，

(北京宇航系统工程研究所，北京 100076)

0 引言

航天型号产品随着研制领域的延展和深入，在发射和飞行过程中要经受愈发复杂苛刻的环境。为确保型号产品在这些环境下能够长期可靠服役，要求对型号上的紧固件产品及其连接可靠性提出严格的要求。

作为航天器结构连接的主要形式之一，紧固连接的可靠性要求不允许有失效的可能，但在实际工程中是很难做到的，因此需要进行可靠性分析，找出可能失效的薄弱环节，采取措施进行纠正和预防。

楔型螺纹螺母产品是用以应对各种复杂可靠环境的一类优良紧固件[1]。而对于楔型螺纹螺母产品在复杂载荷和环境下的可靠性设计需求，仅采用传统应力-强度干涉模型[2]的可靠性设计方法(静态载荷分布参数统计分析方法)已无法满足。因此，为评估楔型螺纹螺母产品的可靠性，本文将针对其特点和可能的失效模式，建立楔形螺纹螺母产品的可靠性评估流程和可靠性理论模型。

1 楔型螺纹螺母产品及其连接形式

1.1 楔型螺纹螺母产品

楔形螺纹螺母是一种新型的自锁内螺纹紧固件产品。楔形螺纹具有独特的结构——在内螺纹的牙底处有一个30°的楔形斜面，当螺栓螺母相互拧紧时，螺栓的牙尖就紧紧地顶在楔形螺纹的楔形斜面上，从而产生了很大的锁紧力，增加防松摩擦力(见图1)。同时，外螺纹牙顶在与楔形螺纹咬合时，牙顶处齿尖易变形，使载荷均匀地分布在接触的螺旋线全长上，避免了普通标准螺纹咬合时，80%以上的总载荷集中作用在第一和第二牙的螺纹面上的现象。因此，楔形螺纹联结副不仅克服了普通标准螺纹联结副在振动条件下易于自松的缺点，而且还使得楔形螺纹的轴向力均匀分布在整个螺纹的旋合长度上，从而提高了整个内螺纹的承载能力，对于延长螺纹连接的使用寿命具有重要意义。

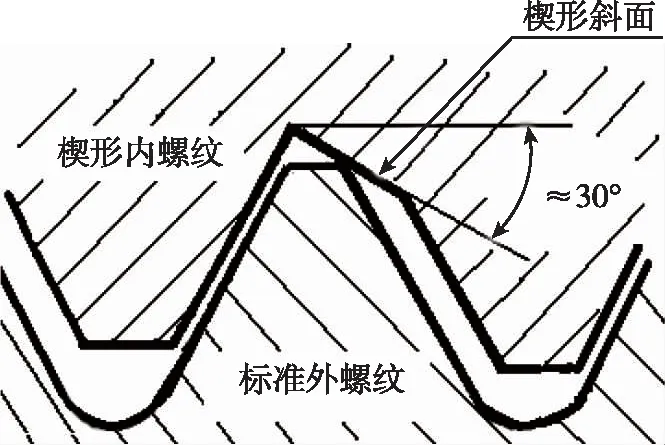
图1 楔形螺纹示意图Fig.1 Wedge screw example

1.2 紧固连接形式

紧固连接用的紧固件，需要承受静载荷和动载荷，要求紧固连接必须具有一定的强度。航天产品结构上典型的紧固连接形式见图2、图3，将上述楔形螺纹螺母与配用螺栓及安装板连接在一起，即构成单个紧固连接。

图2 连接结构示意图Fig.2 Connection structure example

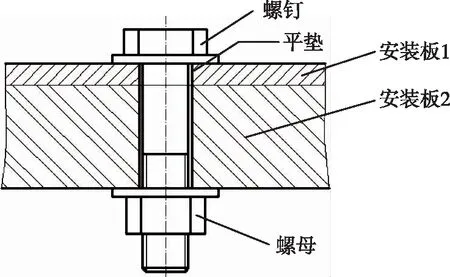
图3 单个螺钉-螺母连接Fig.3 A single bolt-nut connection

2 楔型螺纹螺母产品的可靠性理论模型

2.1 可靠性

可靠性特征量一般包括：可靠度、失效概率、失效率、平均寿命[3]。其中，可靠度是对于可靠性的概率测量，其定义是产品在规定的使用条件和规定的使用寿命内完成规定功能的概率。与可靠度相对应的特征量是失效概率，是指产品在规定的条件下和规定的寿命内未完成规定功能的概率。失效率的定义是产品工作到某时刻尚未失效，在该时刻后的单位时间内发生失效的概率。平均寿命指的是产品使用寿命的数学期望值；对于不可修复产品，平均寿命是指失效前的平均时间[4]。

对于螺栓连接，一般假设其强度与应力均为正态分布，可大为简化可靠度的计算。

2.2 楔型螺纹螺母产品的可靠性评估流程

为评估楔形螺纹螺母产品可靠性，首先需要明确紧固件的主要性能指标，然后确定楔型螺纹螺母产品的可靠性评估方法和要求，通过可靠性模型计算得到可靠性水平。针对楔形螺纹螺母产品的特点，其可靠性评估的分析流程如图4所示。首先，对楔型螺纹螺母产品的特性进行理论分析，然后通过故障树分析(FTA)和故障模式影响及危害性分析(FEMCA)并计算得到可靠性，最后通过试验验证并修正可靠性模型[5]。

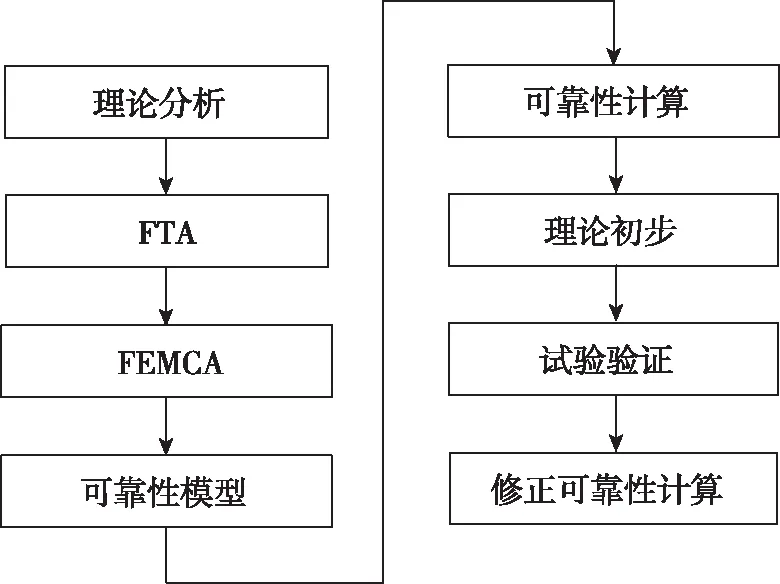
图4 可靠性评估研究流程Fig.4 Reliability evaluation research process

2.3 楔型螺纹螺母的FTA分析

根据紧固件的结构特性和楔形螺纹螺母产品的特点，建立楔形螺纹螺母紧固件的失效故障树模型，如图5所示，其中故障树编号的意义见表1。

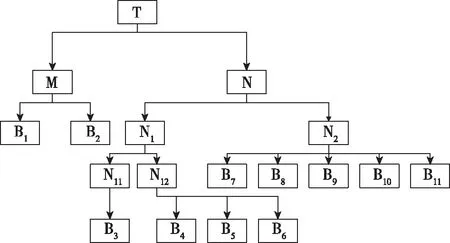
图5 楔形螺母失效故障树模型Fig.5 Wedge screw failure tree mode

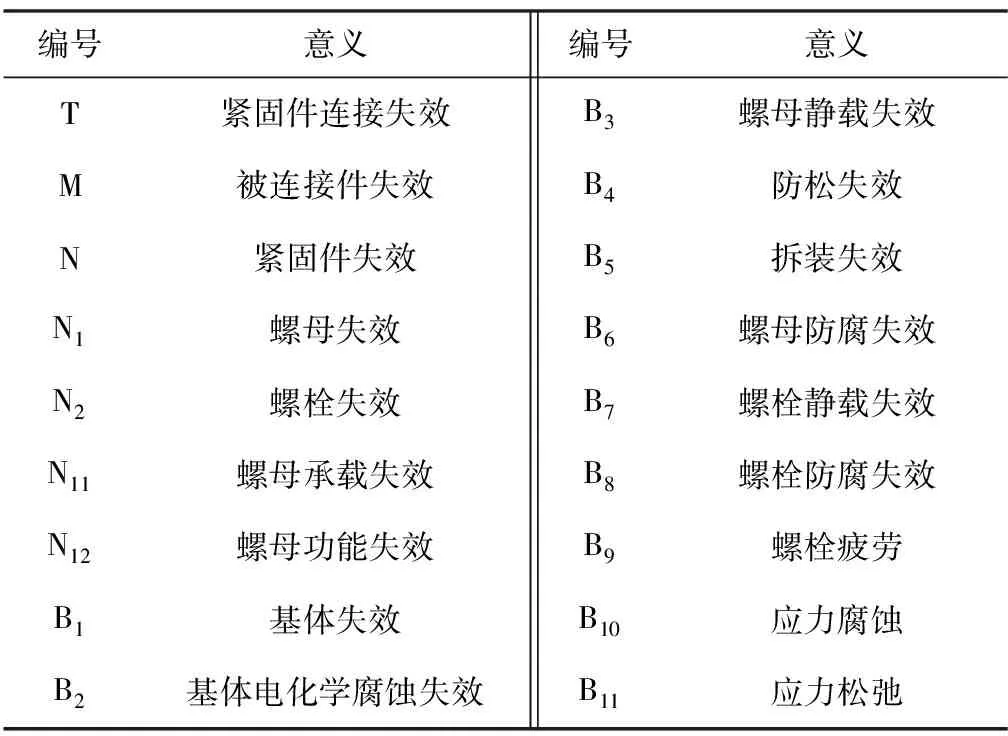
表1 故障树编号意义Tab.1 Failure tree mode symbols

2.4 楔型螺纹螺母连接可靠性模型

进行螺栓连接可靠性设计时，通常根据螺栓连接的使用要求确定设计准则。对于静载可靠度、拆装可靠度的评价，可采用应力-强度干涉模型；对疲劳可靠度的评价，可采用疲劳模型计算。基于上述模型，推导出螺栓连接可靠性的模型和计算公式。对于耐腐蚀可靠度和抗振防松可靠度，试验采用了截尾试验的方法，其评价采用威布尔分布的截尾试验可靠度计算公式。

3 可靠性试验及结果分析

3.1 可靠性试验

为评估楔形螺纹螺母产品可靠性，进行了如下试验：极限抗拉性能试验、疲劳寿命试验、防松寿命试验、拆装寿命试验、应力持久试验以及防腐蚀寿命试验。本文中选用螺纹为M10×1.5；普通外螺纹：8个螺纹牙，材料GH4169；普通内螺纹：6个螺纹牙，材料GH4169；楔形螺纹：6个螺纹牙，材料GH2132楔形螺纹，尺寸标准JB/T 10971-2010[6]。

3.2 可靠性试验结果分析

3.2.1 极限抗拉性能试验

极限抗拉性能的试验结果如表2所示。从表2中可以看出，楔型螺纹螺母的失效形式为螺栓断裂和螺母脱扣。静载失效平均轴力为89.95kN，标准差为1.69 kN，变异系数为0.019。对于静载可靠性的计算采用应力-强度干涉模型，被试组合件的静载可靠性为RT=Φ(zT)>99.9916%。

表2 静载可靠性试验数据Tab.2 Static load reliability test data

3.2.2 疲劳寿命试验

疲劳寿命试验分为两组，第一组完全按照GJB715.30A-2002[7]进行，样本量为10件；第二组对试验件施加安装力矩(68N·m)，试验样本量为18件。带力矩疲劳寿命测试试件失效后的状态可以看到较为明显的贝壳形断口纹理。表3给出了楔型螺纹螺母产品疲劳寿命，由于带力矩状态更好地模拟了组合件在实际使用中的受载状态，使试验件组合体不仅受拉-拉载荷的作用，同时受到剪切载荷的作用，受载情况更为复杂，数据离散度相对较高，疲劳寿命更低，即该方法对可靠性的要求更为严格。因此，本文提出的带力矩状态疲劳寿命测试方法优于标准状态测试方法。

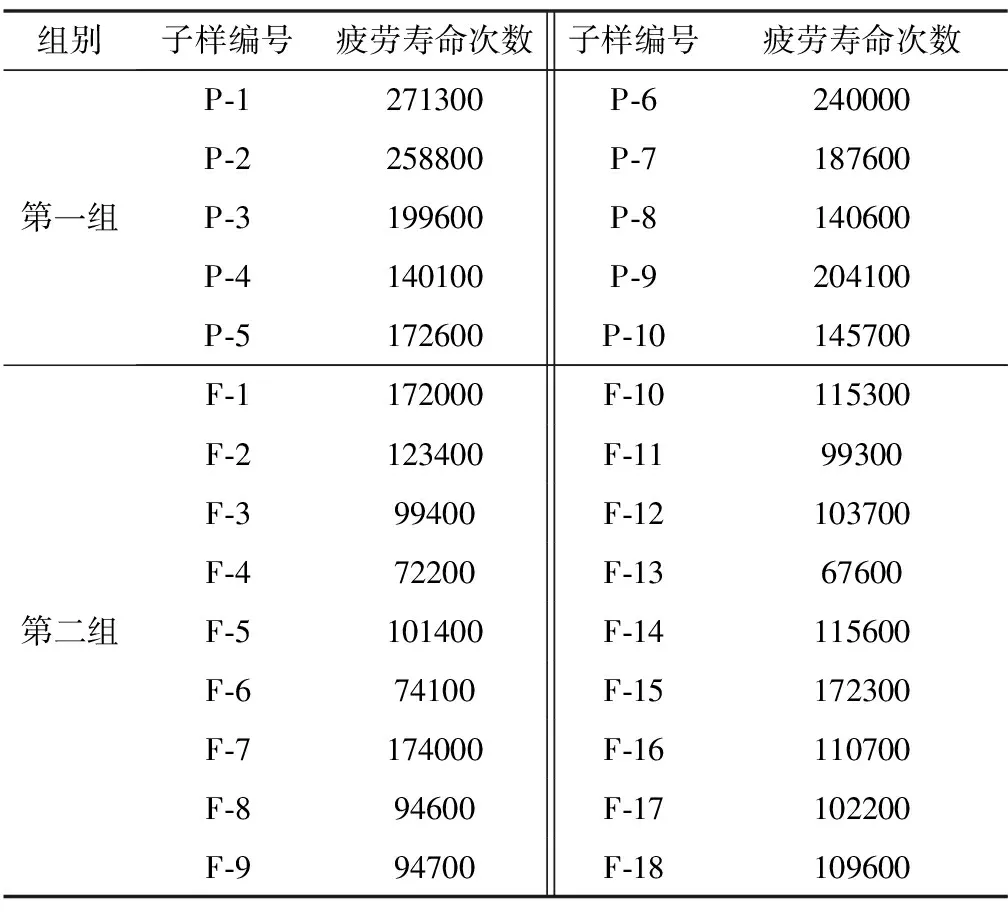
表3 疲劳寿命试验数据Tab.3 Fatigue life test data

3.2.3 抗振防松寿命试验

为对楔型螺纹螺母紧固件组合的抗振防松寿命按照GJB 715.3A-2002[8]进行摸底，在振动循环合格后，继续进行试验。当振动循环达到10次标准试验要求或所有被试件松脱试验停止。试验的安装力矩为40N·m。经过10次标准振动试验后，无一松动，试验后的拆卸力矩见表4。

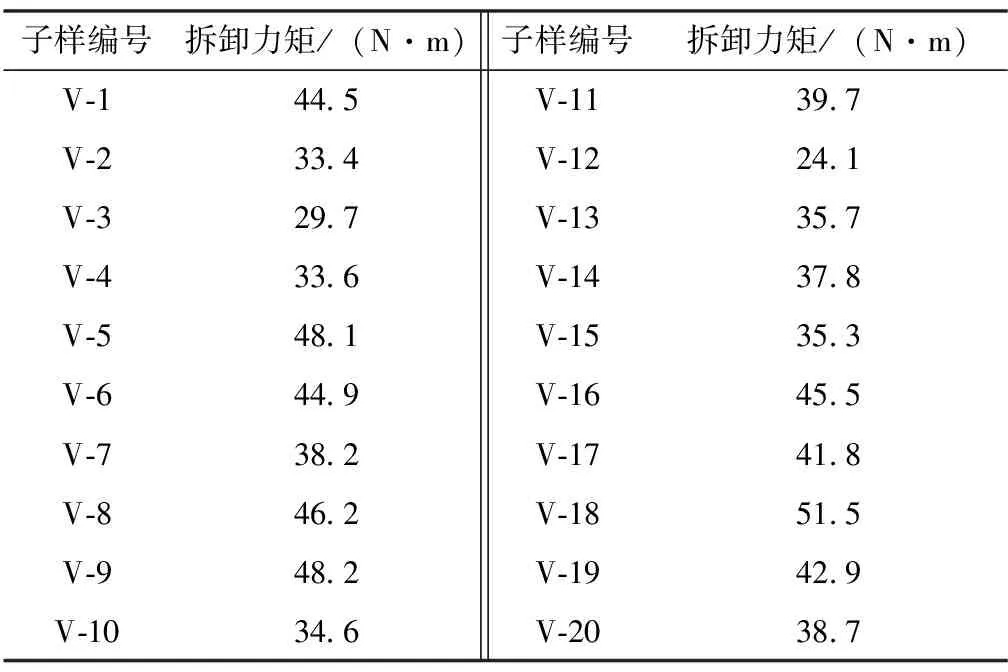
表4 抗振防松寿命试验数据Tab.4 Anti-vibration and anti-loose life test data

根据截尾试验的可靠性计算方法以及常规自锁紧固件抗振防松寿命要求，取任务数=截尾数=300000个循环周期，试验置信度为0.7，投试数量n=20件，为提高安全系数，威布尔分布的特征值取下限，即m=1，由此计算得到组合抗振防松性能的可靠度为：

根据楔型螺纹螺母紧固件抗振防松寿命要求，取任务数=60000个循环周期，其他数据同上，则计算出的抗振防松寿命可靠度为：

3.2.4 拆装寿命试验

拆装寿命试验按照北京宇航系统工程研究所《楔形内螺纹自锁螺母技术条件》标准规定安装力矩进行50次加载试验。由于楔型螺纹螺母紧固件的特点(第一次安装的扭矩系数与其后各次差异较大，随着拆装次数的增加，紧固连接的轴向力不断增大。故将产生的轴向力控制在一定的范围内)，规定以第2次～第5次的平均扭矩系数为标准，各次拆装若扭矩系数与其偏差大于30%，判定失效。其中，扭矩系数K宏观上直接反映螺栓拧紧过程中扭矩与轴力之间的系数，是零件的一个特征参数。拆装寿命的试验数据见表5。对于拆装寿命可靠性的计算采用应力-强度干涉模型，被试件拆装寿命为正态分布，根据工程实践，确定拆装寿命的合格次数为10次，则被试组合件的拆装可靠性为RM=Φ(zM)>98.03%。

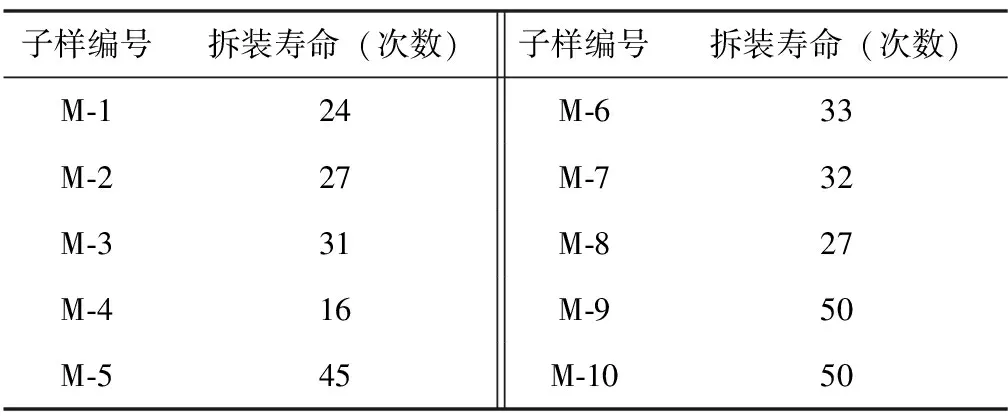
表5 拆装寿命试验数据Tab.5 Dismantling life test data

3.2.5 应力持久试验

参照GIB 715.12-1990标准中的试验要求[9]，应力持久试验时间设为48h，取这一数值作为产品任务数，取试验置信度γ=0.7，投试数量n=20件，为提高安全系数，威布尔分布的特征值取下限，即m=1，将试验数据代入截尾试验的可靠性计算公式，可得应力持久性能可靠性为：

=98.51%

3.2.6 耐腐蚀寿命试验

防腐蚀寿命试验通常通过盐雾试验等方法进行评价，试验中，50%的试件参照GJB 715.1-1989的相关要求[10]，另外的50%施加68N·m的扭矩之后进行试验。施加安装力矩试样的拆卸力矩数据见表6。根据对表面的观察以及对于拆卸力矩的考察，所有20个子样均未发生失效。

表6 带力矩试样拆卸力矩数据Tab.6 Data of disassembly moment of sample with moment

根据GJB 715.1-1989的标准要求[10]，耐腐蚀试验时间为96h，取这一数值作为产品任务数，试验置信度γ=0.7，投试数量n=20件，威布尔分布的特征值取下限，即m=1，将试验数据代入截尾试验的可靠性计算公式，可得耐腐蚀性能可靠性为：

=97.03%

4 结论

本文针对楔型螺纹螺母的特点，根据可靠性初步评估流程完成了对楔型螺纹螺母的FTA分析，建立了其可靠性模型；根据可靠性模型，针对性能设计了相应的试验进行考核，如在标准疲劳寿命试验的基础上，对试验件施加安装力矩进行考核，更贴近实际载荷状态。最终对楔型螺纹螺母需要考核的性能进行了可靠度计算，得到各性能可靠度数据并验证了本文所提出的对楔型螺纹螺母进行可靠性评估的流程及其可靠性模型的正确性。