海洋绞车滚筒优化设计

喻革， 刘厚才

（湖南科技大学 机电工程学院，长沙 410000）

0 引言

滚筒作为海洋绞车主传动系统中的重要零部件。对海洋绞车滚筒进行优化设计一直作为国内外学者研究的重点和热点问题，目前国内外学者针对不同的目标对滚筒进行了各种优化研究。对海洋绞车滚筒的优化研究相对集中在保证强度刚度等要求的前提下，对海洋绞车滚筒进行减轻质量[1]、有限元分析[2-3]、优化结构尺寸[4-5]等方面的研究，并在这些方面取得了一定的研究成果。

海洋绞车作为海上作业中重要的提升设备，广泛应用于水下拖曳系统、水下机器人、海洋钻探、海洋管道铺设、深海石油和天然气等资源勘探和开发过程等海洋作业环境之中。为了保证海洋绞车收放系统能在恶劣的海况下正常平稳地工作，削弱船体升沉运动对吊装物体升沉的影响，使得海洋绞车吊装物在工作时保持在一个水平面上，因此需要海洋绞车具备主动升沉补偿功能。随着对海洋资源的深度开发，越来越多的海洋绞车将具备主动升沉补偿功能。但是目前针对具备主动升沉补偿功能的海洋绞车，对于拥有主动升沉补偿功能而对海洋绞车滚筒进行优化研究的却不常见。主动升沉补偿功能的实现往往需要依靠海洋绞车滚筒频繁正反转，而海洋绞车

滚筒转动惯量是影响海洋绞车滚筒正反转的关键因素，根据所设计的海洋绞车滚筒结构，建立海洋绞车滚筒转动惯量的目标函数，以滚筒结构尺寸、强度、刚度和滚筒稳定性要求为约束，建立滚筒转动惯量最小化的优化模型，最后运用计算机辅助软件Matlab[7]对海洋绞车滚筒转动惯量最小化的优化模型进行求解，得到最优的滚筒结构尺寸。

1 模型的建立

海洋绞车滚筒结构如图1所示。根据结构图可以看出,影响海洋绞车转动惯量的主要因素有滚筒壳体、法兰、滚筒壁件的2个加强筋。

为了方便对滚筒转动惯量运算，根据海洋绞车滚筒结构对海洋绞车滚筒的转动惯量进行简化，本次优化设计将海洋绞车滚筒左右两侧的加强筋看成一块完整的，另外本次海洋绞车设计中可以将主轴的转动惯量忽略，将加强筋的转动惯量忽略。可以得到海洋绞车滚筒转动惯量的表达式：

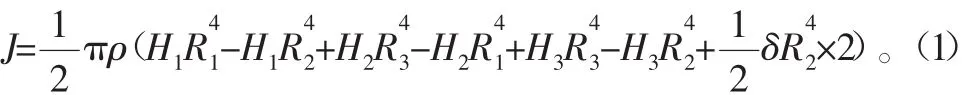
图1 海洋绞车滚筒结构示意图

式中：H1为海洋绞车滚筒壳总长度；R1为海洋绞车滚筒绳槽半径；R2为海洋绞车滚筒内径；H2为左侧法兰厚度；H3为右侧法兰厚度;R3为法兰半径；δ为滚筒壁厚；ρ为钢密度。

按照GB 3128-82船舶技术绞车设计标准[8]，卷筒法兰高度必须超出最外层缆绳的高度，超出值应不小于钢丝绳直径的2.5倍，即

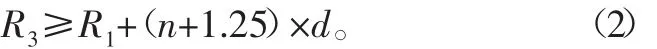
根据海洋绞车滚筒的滚动惯量的计算公式可知，当使得R3越小的时候，可以使得整个海洋绞车滚筒的转动惯量越小，所以本次优化设计中取最小值，即

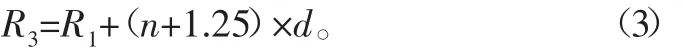
同时假设海洋绞车滚筒壁厚为δ，则

H2、H3为海洋绞车滚筒法兰厚度，滚筒法兰厚度与滚筒壁厚的关系[9]为

将海洋绞车滚筒壳体的长度分为三部分，第一部分为脐带缆在滚筒壳体上缠绕部分长度Lj，第二部分为2个法兰的厚度，以及末端和刹车系统有关的部分。得到其关系式为

根据本次海洋绞车的刹车系统设计，其中h的长度为固定值，h=450 mm，可以得到：

H4、H5为海洋绞车滚筒的加强筋厚度，在海洋绞车进行设计的时候，令滚筒加强筋的厚度等于海洋绞车的滚筒壁厚：

将上述关系式代入到海洋绞车转动惯量计算公式中，最后可以得到海洋绞车滚筒转动惯量的目标优化函数J：

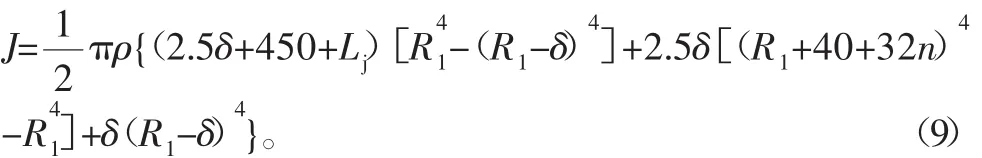
式中：δ为滚筒壁厚；R1为滚筒绳槽半径，n为脐带缆缠绕层数，Lj为脐带缆在滚筒壳上的缠绕长度。

本次海洋绞车滚筒转动惯量优化设计选取R1、Lj、n、δ作为变量，在满足设计参数、绞车滚筒强度、滚筒稳定性等要求的前提条件下求出海洋绞车转动惯量优化函数的最小值。

2 约束条件

针对本次海洋绞车滚筒转动惯量最小化的优化，可以将主要设计参数、滚筒强度要求、稳定性要求等作为本次海洋绞车滚筒转动惯量优化设计的约束条件。

海洋绞车的主要设计参数：缆绳直径为32 mm，工作载荷为200 kN，储缆滚筒容绳量为4500 m，适用于4级以下海况，安全工作载荷为138 kN，最快提升速度为第10层100 m/min，底层60 m/min，卷筒储缆容绳量为4500 m，脐带缆直径为32 mm，主动升沉补偿能力为±3 m。

根据本次海洋绞车设计为单件生产，且设计要求海洋绞车滚筒储缆4500 m，可知海洋绞车滚筒为大尺寸滚筒，海洋绞车滚筒的生产可以选择用Q345钢板通过设备卷弯成圆筒，再进行焊接[10]。

1）要求满足设计参数要求：本次海洋绞车设计的缆绳长度为4500 m，同时随着滚筒的长度和直径的变化，所缠绕的圈数也是随着变化的。同时为了满足直径DLS=32 mm脐带缆最小弯曲半径要求（最小弯曲直径大于900 mm）,以及本次海洋绞车滚筒驱动方式为6台电动机驱动，考虑到6台电动机的布局方式，得到本次海洋绞车优化设计需要取D1≥1000 mm。

假设所缠绕的层数为n层，则海洋绞车滚筒储缆第n层的直径为

先算出第1层绞车滚筒缠绕脐带缆长度：

第1层缠绕长度：L1=πD1Lj/d；

第n层缠绕长度：Ln=πDnLj/d；

总共n层平均缠绕总长度：（L1+Ln）×n/2。

海洋绞车脐带缆总长度为

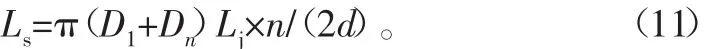
由此可以得到：

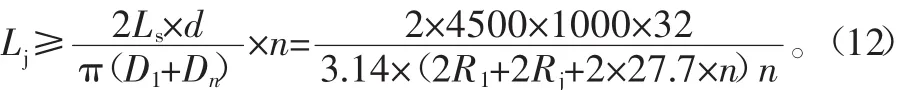
在实际脐带缆缠绕过程中，脐带缆所缠绕的层数只能是整数层数，因此在本次优化设计计算海洋绞车滚筒缠绕层数的时候需要取整数，即n需要向上取整。

2）要求满足海洋绞车滚筒强度设计要求[11]。

当L≤3D1时，海洋绞车滚筒受到的弯曲和扭应力合成应力不超过10的压应力，所以只需要计算压应力即可。在计算海洋绞车压应力的时候需要增加一个S=1.5的安全系数，最后可以得到：

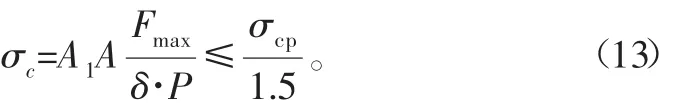
当L＞3D1时，海洋绞车滚筒受到弯曲应力和扭应力超过了10的压应力，不能忽视，在计算受到的载荷的时候需要增加一个S=1.5的安全系数，最后可以得到其合成应力：

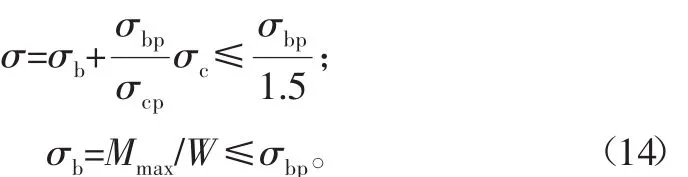
式中：Mmax为由脐带缆最大拉力引起滚筒的最大弯矩，N·mm；W为抗弯截面模量，mm3。

最后得到：

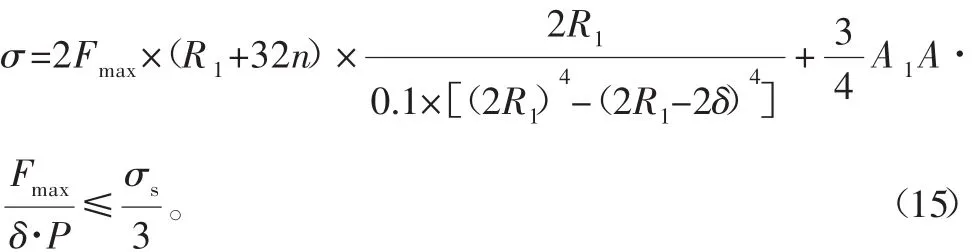
式中：L为滚筒长度；D1为滚筒绳槽直径；n为滚筒缠绕层数；δ为滚筒壁厚，Fmax为最大拉力；A为滚筒缠绕系数；σs为Q345的屈服强度。

3）要求满足海洋绞车滚筒稳定性设计要求。

在海洋绞车滚筒的设计过程中，不仅要保证滚筒壳体的应力小于规定的应用值，同样也要保证滚筒具有足够的稳定性[12]。

当海洋绞车滚筒的直径D≥1200 mm且滚筒壳体长度L＞2D时，海洋绞车滚筒为大尺寸滚筒，必须对海洋绞车滚筒壁的稳定性进行校核，如果当稳定性不满足要求的时候，需要增加滚筒的壁厚来增加海洋绞车滚筒壳体的稳定性。海洋绞车稳定性[13]应满足如下条件：

海洋绞车滚筒失去临界时的条件压力为

海洋绞车滚筒壁单位压力为

海洋绞车滚筒稳定系数为

在本次海洋绞车滚筒转动惯量优化设计过程中，需要给海洋绞车滚筒的稳定性系数增加一个S=1.5安全系数，最后得到稳定性的满足条件为

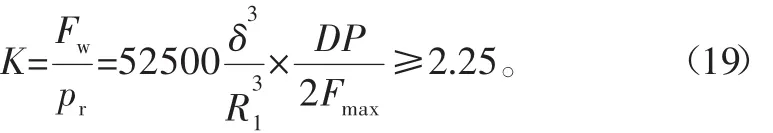
式中：Fmax为脐带缆最大静拉力，N；D为滚筒绳槽底径，mm；P为脐带缆卷绕节距，mm；δ为滚筒壁厚，mm；R1=D/2，mm。

4）海洋绞车实际缠绕层数。在海洋绞车实际的缠绕过程中，脐带缆缠绕滚筒的层数不宜过多，脐带缆缠绕滚筒层数过多会导致乱绳[14]的情况出现，在实际生产过程中一般为6~12层，所以有：6≤n≤12。

3 海洋绞车滚筒优化模型的求解

根据目标函数以及约束条件建立了本次海洋绞车转动惯量最小的优化模型，将所建立的优化模型运用Matlab优化工具箱的fmincom优化函数[15]进行运算求解，将计算得到的转动惯量的优化解与原始设计解列于表1中。

根据原始方案结构与优化设计结果方案对比可知，在保证海洋绞车的设计参数、满足绞车的强度、稳定性的前提下，海洋绞车滚筒转动惯量优化设计结果相对于原始设计结果，降低了20.4。

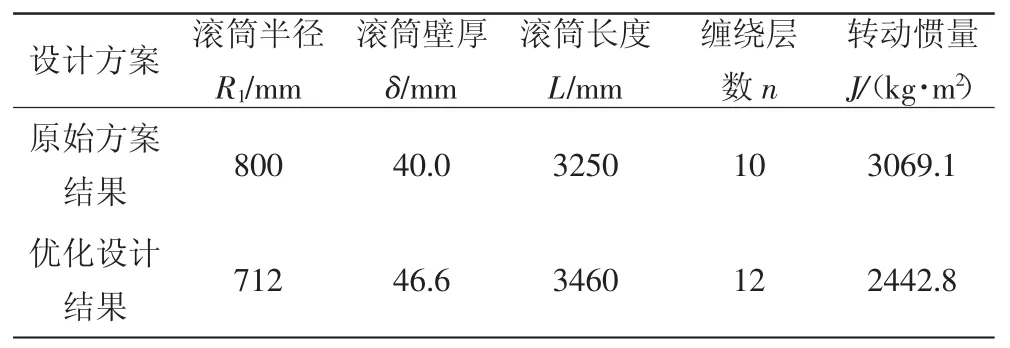
表1 优化设计解与原始设计解对比

4 结 语

针对具备主动升沉补偿功能的海洋绞车，通过对海洋绞车滚筒的转动惯量建立最小化的优化模型，运用Matlab软件优化工具箱的fmincom优化函数对海洋绞车滚筒转动惯量的优化模型进行求解，得到最后的求解结果。结果表明在满足设计参数、绞车的强度、稳定性的前提下海洋绞车滚筒的转动惯量明显减小了，对拥有主动升沉补偿功能的海洋绞车滚筒频繁正反转有很大的益处。同时对以后拥有主动升沉补偿功能的海洋绞车滚筒设计具有一定的指导意义。但是在进行海洋绞车滚筒转动惯量的优化设计过程中，由于对问题的简化，所建立的优化模型只考虑了影响转动惯量的主要因素，并未把全部因素考虑进来，需要在以后的工作中将整个海洋绞车的结构全部考虑再做更深一步的研究。