基于LPV模型的麦弗逊式主动悬架控制器设计
2018-07-30赵强,何法
赵 强,何 法
(1. 东北林业大学 交通学院,黑龙江 哈尔滨 150040; 2. 华晨公司汽车工程研究院,辽宁 沈阳 110141)
0 引 言
主动悬架通过采用主动伺服作动器,由外界提供能量,能够根据汽车行驶条件动态自适应调节悬架的刚度和阻尼系数,兼顾车辆的操作稳定性和行驶平顺性,还具有可控车身高度等优点,一直是行业内学者和车企的研究重点之一。包括奔驰、保时捷、丰田、福特等在内的国际著名车企都致力于主动悬架的开发与研究,并将不同类型主动悬架系统应用到各自的车辆上,这些车企一般都有自主研发的高端主动悬架产品。比如:2010年德国大众汽车公司将最新研发的空气悬架系统应用到途锐车型上;2013年本田将研发的主动可调后悬架系统(ADS)首次应用到思域旅行车上,其悬架系统能根据载重情况设置不同的工作模式;雪铁龙C5和C6车型采用其第3代的Hydractive液压式主动悬架系统;奥迪A6L、A8车型采用可调空气式主动悬架,奥迪TT、R8车型则采用电磁式主动悬架;2015款凯迪拉克XTS车型装配了其第3代MRC主动式电磁悬架系统。
主动悬架研发主要包括悬架结构参数优化和控制方法设计[1]。结构设计优良的悬架也必须配以最优的控制器才能达到其最佳性能,且优秀的控制算法一般对各种形式主动悬架都有应用价值或借鉴作用。所以,深入研究主动悬架的控制算法变得尤为重要。目前主动悬架控制方法的研究包括:天棚及其改进控制[2]、模糊控制[3-4]、最优控制[5]、预测控制[6]、预瞄控制和鲁棒控制等[7-9]。以上研究几乎都基于1/4车(quarter car)的两自由度模型,该模型是简化的线性模型,且未考虑具体悬架形式(如麦弗逊、多连杆型等)的物理特性影响,例如具体悬架几何关系所带来的固有非线性。针对上述线性两自由度模型所设计的控制算法在应用到具体悬架上的控制效果和实用性有待检验。因此,笔者基于主动悬架具体形式设计了合适的鲁棒控制算法。
麦弗逊悬架具有结构简单紧凑、体积小、经久耐用等优点,是当今应用最广泛的悬架之一。国内众多常见车型,如标致307、卡罗拉、君越、迈腾、高尔夫6和现代ix35等均采用麦弗逊式悬架。笔者建立了麦弗逊式主动悬架LPV模型,针对该模型采用LMI技术和区域极点配置法设计状态反馈H∞控制器,提高悬架性能。
1 麦弗逊主动悬架动力学分析
麦弗逊式悬架系统的结构如图1,主要由控制臂5、减振器3、车身2(簧载质量)、主轴和轮胎4(非簧载质量)组成。图1中:zs表示车身垂向位移运动;d表示减振器上体和下体的相对运动;θ1表示控制臂和减振器之间的旋转运动;θ2表示减振器和车身之间的旋转运动。
由于控制臂质量远远小于簧载质量和非簧载质量,因此忽略不计,同时忽略其柔性变形。则在图1中添加伺服作动器,并假定螺旋弹簧、轮胎变形和阻尼力都在线性区域内变化,形成二维麦弗逊式主动悬架简化模型如图2。图2中:伺服作动器(其产生的主动力为fa),被动元件弹簧(其刚度为ks)和阻尼器(其阻尼系数为cp)并联形成主动悬架的滑柱;ms为簧载质量;mu为非簧载质量;kt为轮胎刚度;fd为负载扰动;zs为车身垂向位移;zr为路面垂向位移;θ0为平衡点控制臂的初始角位移;α′为平衡点时减振器上端点与坐标原点连线和控制臂之间的夹角;θ为控制臂的角位移。
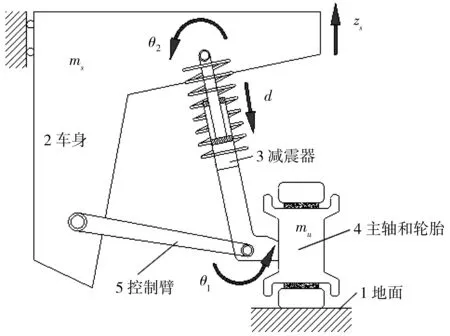
图1 麦弗逊式悬架机构Fig. 1 Mechanism diagram of Macpherson suspension
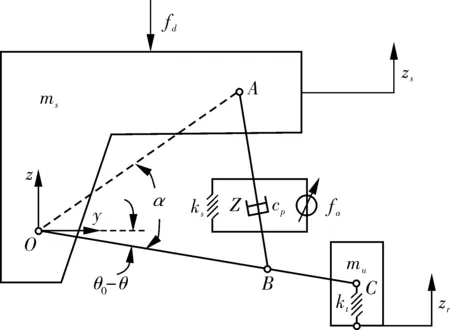
图2 二维麦弗逊式主动悬架简化模型Fig. 2 Simplified model of 2-D Macpherson active suspension
该模型为从实际麦弗逊悬架物理模型抽象出的几何结构,与传统线性两自由度模型相比,考虑了悬架具体几何关系所带来的固有非线性特性,因此该模型更准确,更接近于实际悬架。由于图2 模型具有两个独立自由度,考虑到用zs和zr描述系统更方便简洁,故为广义坐标。应用含耗散能的拉格朗日方程建立悬架的运动微分方程,首先由动能定理可求得主动悬架系统的总动能,如式(1):
(1)
由弹性势能基本公式可得到主动悬架系统总势能,如式(2):
(2)
麦弗逊式主动悬架系统减振器中含有阻尼器,其产生的耗散能如式(3):
(3)
含耗散能的拉格朗日方程[10-11]如式(4):
(4)
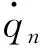
将式(1)~(3)带入式(4),可得二维麦弗逊式主动悬架的动力学方程,如式(5)、(6):
kt{zs+lC[sin(θ-θ0)-sin(-θ0)]-zr}=-fd
(5)
ktlCcos(θ-θ0){zs+lC[sin(θ-θ0)-sin(-θ0)]-zr}-
(6)
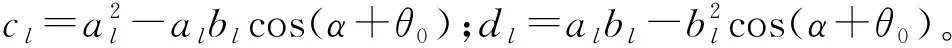
(7)
式中:
矩阵中的参数a21、a23、a24、a41、a43和a44的表达式限于篇幅不再展开。
2 LPV模型的极点配置状态反馈鲁 棒控制
2.1 基于LMI区域极点配置
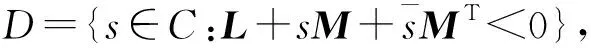
其矩阵值函数如式(8):
(8)
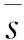
定义2[12-13]:对复平面中给定的左半复平面的子区域D和矩阵A,如果矩阵A所有特征值都位于区域D内,则称矩阵A是D-稳定的。
定义3:矩阵Kronecker乘积[12-13](矩阵张量积)对两个给定的矩阵A=(aij)∈Rn×m和B∈Rp×q,矩阵A和B的Kronecker乘积是一个分块矩阵A⊗B=(aijB)∈Rnp×mq。
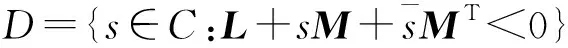
复平面上半径为r,圆心在(-q,0)的圆盘D(r,q)为一个LMI圆盘区域,如图3。
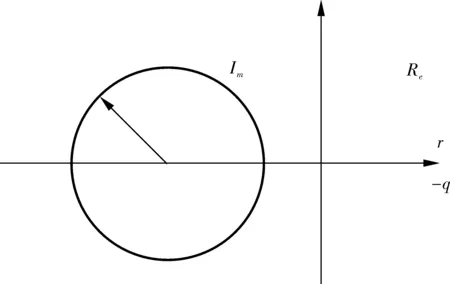
图3 圆心在(-q,0)半径为r的圆盘区域Fig. 3 Disk domain with center at(-q,0)with radius r
该区域用线性矩阵不等式描述其LMI区域,如式(9):
(9)
由r>0可推出:
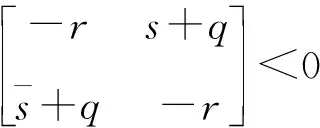
(10)
因此它的特征函数如式(11):
(11)
由式(11)可得:
MD(A,X)=L⊗X+M⊗(AX)+MT⊗(AX)T=
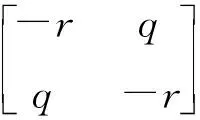
(12)
由以上分析能得出推理:矩阵A的所有特征值均在半径为r,圆心在(-q,0)的圆盘中充分必要条件是存在对称矩阵X>0,使得:
(13)
2.2 LPV系统的区域极点配置控制
LPV(linear parameter varying)是线性变参数系统,LMI的发展推动了基于LPV系统的鲁棒控制在工程实践中应用,其克服了传统控制缺点,能保证系统全局稳定性。考虑带有k个线性无关的变量参数θ=[θ1,…,θk]T的 LPV 系统G(θ)如式(14):
(14)
式中:x∈Rn为状态向量;u∈Rn为控制输入向量;w∈Rn为扰动输入向量;z∈Rn为性能输出向量;y∈Rn为系统输出向量;参数θ=[θ1,…,θk]T为时变的参数序列,代表系统的不确定性或者系统的动态变化,也是系统所依赖的参数;A、B1、B2、C1、C2、D11、D12、D21、D22为关于变参数θ的仿射函数,θi为θ=[θ1,…,θk]T的线性仿射函数。
对式(14)的时变变参数系统,给定γ>0,通过状态反馈u=Kx,若存在一个对称矩阵X和矩阵L=KX,使得以下不等式约束成立:
(15)
(16)
若式(15)、(16)对多胞体模型各个顶点优化问题有解,则所求状态反馈增益K=LX-1不仅可保证闭环的极点落在所设置的圆盘区域L(q,r)之中,而且也能保证闭环的扰动抑制具有最小的H系能指标γ。根据所求得凸多胞形结构系统LPV的区域极点配置的状态反馈H的控制器为:K=LX-1,上述不等式约束可通过 LMI 优化软件(如 LMI Control Toolbox)求解[14]。
2.3 基于LPV的主动悬架H∞控制
以某车型的麦弗逊式悬架为研究对象,其基本参数如下:ms=453 kg;mu=71 kg;cp=1 950 N·s/m;ks=17 658 N/m;kt=183 887 N/m;lA=0.66 m;lB=0.34 m;lC=0.37 m;θ0=12°;α=50°。
根据式(5)、(6),考虑非线性项sin2(θ-θ0)和簧载质量ms的不确定性,其他参数均已知。由被动麦弗逊式悬架的仿真结果可知θ的取值范围,并且已知θ0的值,即可确定sin(θ-θ0)的范围。令n=sin2(θ-θ0),可得参数矩阵φ∈[msn],其中ms∈[msminmsmax],n∈[nminnmax]。
麦弗逊式主动悬架的LPV模型可用多胞体的4个顶点如式(17):
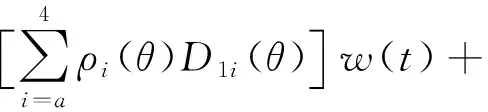
(17)
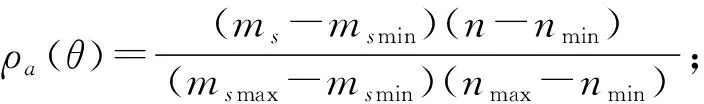

针对麦弗逊式主动悬架的LPV系统的状态空间模型,将闭环系统的极点限制在左半平面圆心为(-60,0)、半径为50的圆盘区域内,并利用 MATLAB中的LMI 工具箱的相关命令函数可求解得到极点配置的状态反馈鲁棒H控制器K,K=[-491.204 2 -121 9.921 6 121.965 4 -11.465 7 ]无论簧载质量在317 kg到589 kg范围如何变动,此控制器不仅可保证闭环的极点落在圆盘区域L(q,r)之中,且可保证闭环的扰动抑制具有最小H性能γ=1.983 1,此控制器是利用LMI技术求解麦弗逊主动悬架LPV的极点配置的状态反馈控制器。
3 仿真分析
选择C级路面的不平度来建模,车速取40 km/h,麦弗逊式悬架的簧载质量设置为标称质量453 kg,根据2.3节中给出的悬架参数,在Simulink平台中建立麦弗逊主动悬架仿真模型,如图4。
选取路面激励模型作为路面输入zr,得到车身加速度和控制臂角位移响应曲线,如图5。
由图5可看出:在随机路面激励下,麦弗逊主动悬架相比于同参数的被动麦弗逊悬架和模糊PID控制的麦弗逊悬架,其车身加速度和控制臂角位移的峰值都有所减少。其计算对应的均方根值如表1。
由表1可看出:主动麦弗逊悬架与其被动形式相比:车体质心垂直加速度减少了13.48%;控制臂角位移减少了大约17.58%;而其与模糊PID控制主动悬架相比,虽然加速度增加了11.12%,但控制臂减少了24.68%,明显降低了车身振动幅度。
根据图5中的数据,绘制车身加速度和控制臂角位移的功率谱密度曲线,如图6。
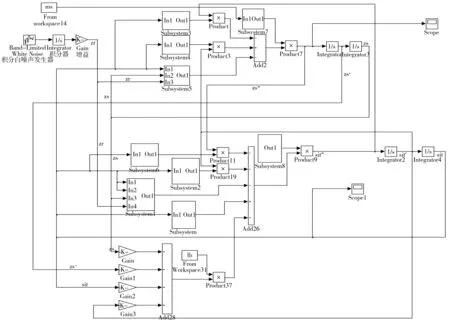
图4 麦弗逊主动悬架simulink模型Fig. 4 Simulink model of Macpherson active suspension
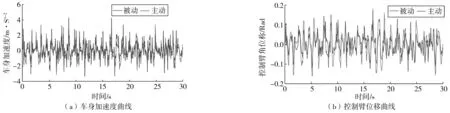
图5 车身加速度和控制臂位移曲线Fig. 5 Vehicle body acceleration and angular displacement of control arm

图6 功率谱密度曲线Fig. 6 Power spectral density curve
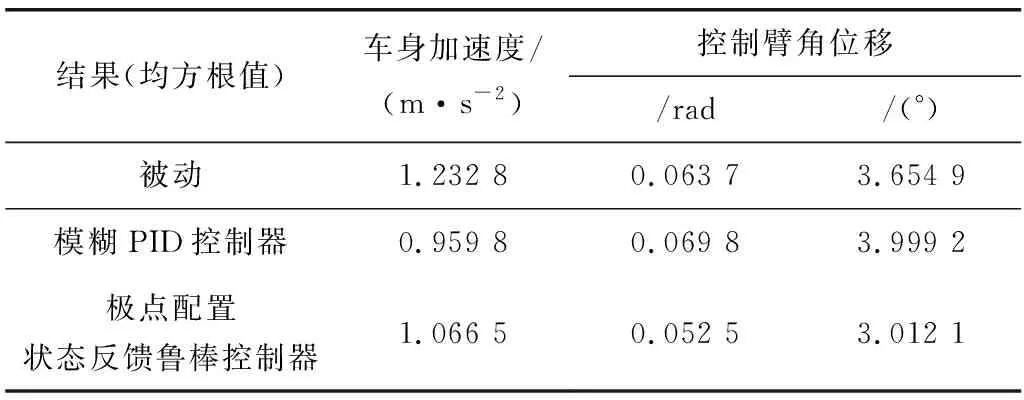
结果(均方根值)车身加速度/(m·s-2)控制臂角位移/rad/(°)被动1.232 80.063 73.654 9模糊PID控制器0.959 80.069 83.999 2极点配置状态反馈鲁棒控制器1.066 50.052 53.012 1
由图6可看出:在随机路面的激励下,主动麦弗逊悬架相比于被动麦弗逊悬架在4~8 Hz范围内,其车身加速度和控制臂角位移功率谱密度峰值较小,因此从频域内进一步验证主动悬架提高了车辆的平顺性和悬架的稳定性。
将模型中的簧载质量标称值分别改为最小值317 kg(空载)和最大值589 kg(满载),并以阶跃函数代替模型中的随机路面输入,分别得到车身加速度和控制臂角位移的响应曲线,如图7。

图7 车身加速度和控制臂角位移Fig. 7 Vehicle body acceleration and control arm angular displacement
由图7看出:参数簧载质量取最小值和最大值时,所设计的极点配置状态反馈鲁棒控制器均适用,与被动麦弗逊悬架相比,能降低车身加速度和控制臂角位移幅度,进一步提高车辆行驶平顺性和悬架稳定性。
4 结 语
笔者运用拉格朗日方程分析简化的二维麦弗逊悬架模型,并推导出麦弗逊悬架的运动学方程,并针对簧载质量的不确定性,建立麦弗逊式主动悬架的LPV模型,应用LMI技术和区域极点配置方法完成了状态反馈鲁棒控制器设计。仿真分析验证了带有极点配置的状态反馈鲁棒H∞控制器的麦弗逊式主动悬架车辆行驶平顺性和稳定性明显优于参数相同的被动麦弗逊式悬架。
