加强AdSEn鲁棒性的实验设计
2018-07-30张正
张 正
(温州职业技术学院 电气电子工程系,浙江 温州 325035)
0 引 言
传统的过程能力指数(CPK)方法[1]假设前提是数据样本独立,且分布相同,然而,这在现实应用中较难保障,在日益多维化的数据冲击下已显得力不从心。鉴于CPK方法的局限性,其在高精度、高相关性的过程能力控制环境中并不完全适用。
调整样本熵AdSEn(Adjusted Sample Entropy)源于样本熵,由香农信息熵发展而来,用于检测数据的复杂度和混乱度,有应用于过程能力监测的前景[2-3]。AdSEn能通过可控数据段熵值与目标数据段熵值相除的商作为量化指标,且已被证实在理想的等权重多变量环境下,可得到较好的结果[4],但考虑到多变量环境中每个变量的真实影响并非全都一样[5],其在应用中完全取代CPK的优势尚未形成。本文针对AdSEn的算法原理,辅以鲁棒性实验设计,寻找最适合AdSEn方法的鲁棒性实验设计方案,提高AdSEn在过程能力控制上的实用性。
1 相关算法
1.1 样本熵算法
样本熵值测量原有数列与新数列中,超过阈值的事件发生概率的比值负对数记为:

作为CPK的应用,可假设d [ui-uj]为样本与目标值之差的绝对值。若目标为期望值,可单个数据为对比对象,也可取一段数据的平均值为对比对象;标准差为目标,则需求一定量样本的标准差与目标标准差的距离。从样本熵算法中可发现,一条公式、一个指数无法同时反应期望值与标准差的变化。
1.2 AdSEn算法
AdSEn算法对样本熵的输入进行调整,旨在将标准差和期望值的变化都融入到一个变量中去[6]。设样本熵的元输入为xij,调整变换后的输入为yij。记第i样本组为xi,xij为xi中第j个样本, 为xi的均值。通过变换可将元样本x中的变量变化添加到yij的均值变化上,且不改变元样本分布。
1.3 田口方法
田口方法是一种基于响应面的方法,将变化的诱因归为可控因子和难控因子(即噪声因子)两类,旨在通过探究可控变量组合以削弱噪声对实验结果影响的研究,比想办法改变或者消除难以控制的噪声因子更简单有效,且成本更低[7]。田口方法建立了一组交叉数列,并分析信号-噪声比SNR(Signal-to-Noise Ratio),SNR比值越低,对应的参数组合所得的实验结果越稳定。然而,田口方法并不能真正反馈连续性参数实验情况下的最优解,且这种高低组合的2k实验设计可能会导致模型匹配过程中的误差,实验契合度值得商榷。在应用过程中上述困难亟待解决。
由于田口方法的局限性,相关研究并未得到更多关注。然而,在参数健壮性设计RPD(Robust Parameter Design)领域的探索并没有停止。通过定量实验方法探索诸如PerMIA方法、Derringer方法和双响应(Dual Res)方法等类似田口方法的手段与AdSEn结合,可降低不可控噪声因子对实验响应结果的影响,寻找提高AdSEn鲁棒性的最佳实验设计方案。
2 实验设计
结合多变量环境,在田口方法的多变量应用的基础上,通过量化的对比研究,探索AdSEn与类似田口方法的PerMIA方法、Derringer方法和双响应方法的结合,对三种设计方案进行实验比较。通过量化结果寻找AdSEn在过程能力控制上的最佳实验设计方案,论证与AdSEn结合的适用场景,从而使AdSEn能更加适应高密度数据采集的工业环境。
2.1 实验背景
以美国某炼钢厂一套炼钢工艺为例,该工艺含有5个变量,包括最高加热温度、加热时间、转运时间、轧钢时间及不可控噪音变量,仅以煺火油温为例加以说明。为确保数据的充分性和实验的可重复性,利用微软Access软件模拟生成生产环境随机数据,以人工随机算法数据模拟不可控噪音,以可控参数作为输入变量,通过对高、低实验参数的设置,得到模拟的最终结果。其实验设计参数见表1。

表1 实验设计参数
轧钢工艺的田口交叉数列[8]见表2。在田口方法中,需要找到SNR值最小的对应组合,即组合设计ABCD=(-, -, +, +),使实验受到的噪音影响最小。
2.2 AdSEn与PerMIA方法的结合
PerMIA方法是一种与田口方法类似基于响应面实验设计的方法,也采用交叉数列的设计,不同之处在于PerMIA是建立两组分开的模型:一组实验模型针对实验响应的期望值y的变化,另一组实验模型针对实验响应的变化因子S(如方差、标准差等),旨在将影响因子归类为噪音相关因子和调整相关因子。通过实验设计可找到两种因子,选择其中对变量影响最小和最接近标准期望值的参数配置,以获得最优实验参数设置。实验采用类似2k实验设计,记录高、低噪声情况下的输出。高噪声组记为“+”,计3次实验:(+1, +2, +3);低噪声组记为“-”,计3次重复实验:(-1, -2, -3),如图1所示。
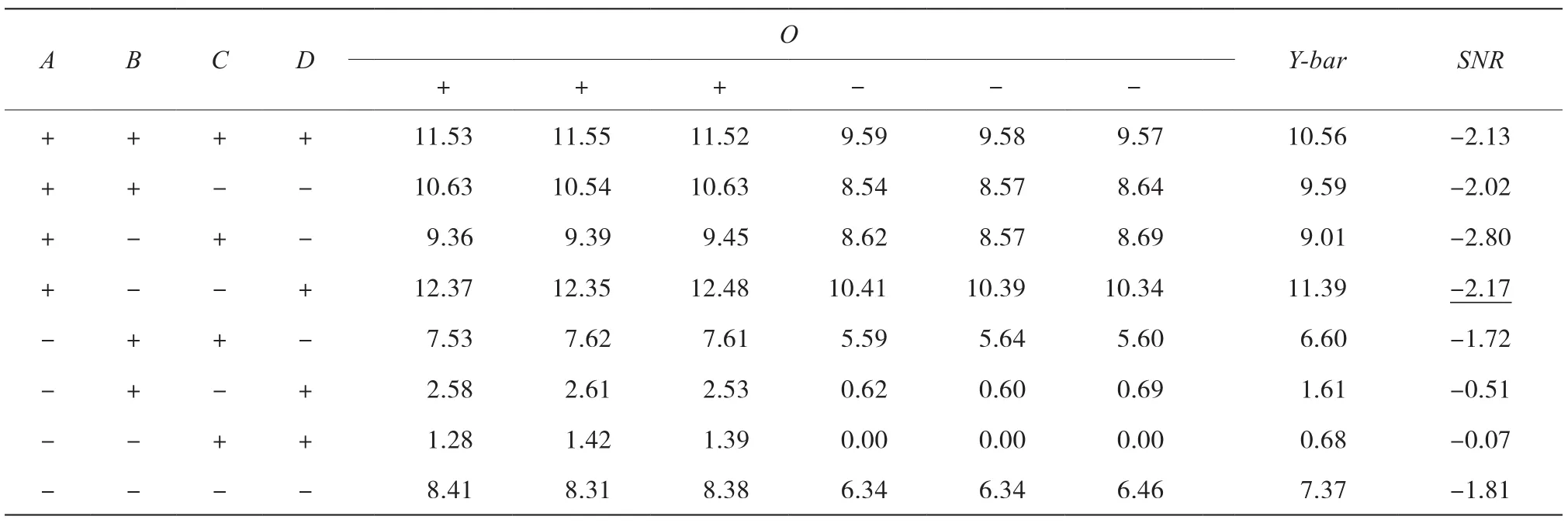
表2 田口交叉数列

图1 PerMIA方法的交叉矩阵
线性模型由统计软件Minitab生成,Minitab能输出线性模型分析结果(见表3)。
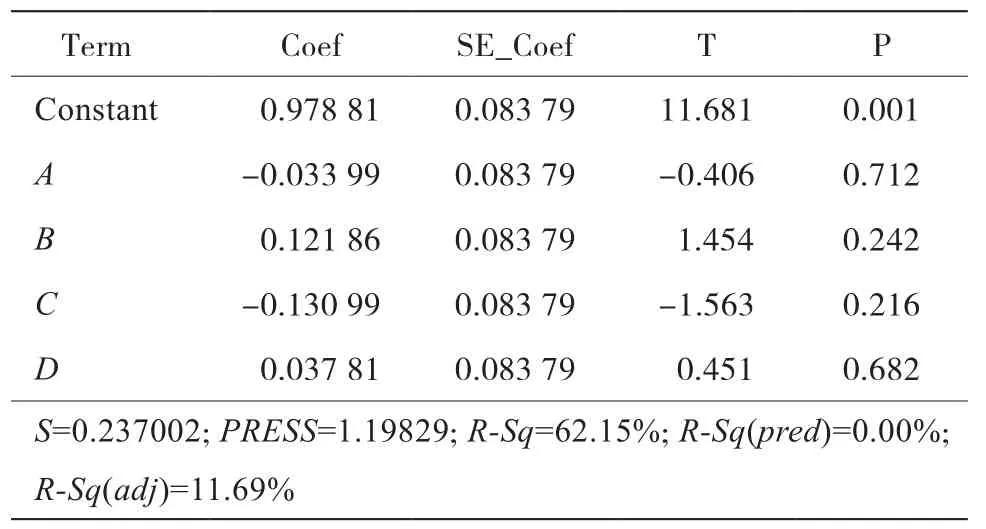
表3 线性模型S的主要成分
R-Sq(adj)为调整后的R2,即其比值越接近1,意味着模型的SSerror越小。调整后的R2,即R-Sq(adj)为旨在 消除新增变量对交叉模型的影响。当R-Sq(adj)越小,模型与响应面的匹配越弱。因此,需要进行一系列假设检验以估算噪声相关因子S,这里S即为标准差。
由于此例只有8个标准差或中点,无足够的自由度来运行全模型或交点测试,因而只能依次测试6个不同的交点和4个不同的均值测试。PerMIA方法测试显示,AD和BC的交叉组合的R2值非常高,据此可判定在D=ABC模型中,AD和BC是有相关性的两对变量。由于B, C的显著性(P值结果)比A, D的显著性更高,可选择BC为模型中的交叉因子,得到模型:

用同样的方法可得到均值Y的模型:

其结果见表4。
由(1)式可得,当(B, C)被设计为(-1, 1)时,变化最小,将B, C的参数设置值代入(2)式时,期望目标值为8, (2)式可变形为:Min(Y-8)2。由上述实验结果,以Min(Y-8)2为目标方程,求最优解。通过线性运算模型在Excel Solver中的结果,可得到结论:当(A, D)=(0, -1)时,均值最接近Y=8。

表4 MINITAB关于y-均值的ANOVA输出
2.3 AdSEn与Derringer方法的结合
Derringer方法与PerMIA类似,它将响应面模型的结果转换为若干条独立的渴望度目标方程(Individual Desirability目标为di),各条独立的渴望度方程都有自己的渴望度di,然后将各di整合为一条总渴望度目标方程D,D的取值范围为D∈[0, 1],越高的总渴望值说明其结果更理想。
当总渴望值最大值为理想值时:
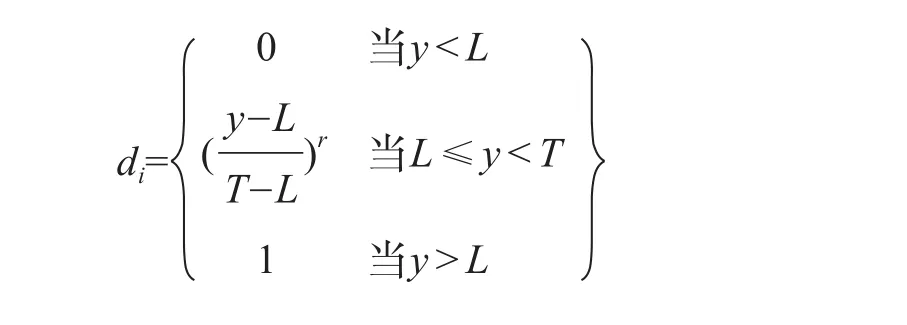
当总渴望值最小值为理想值时:

当总渴望值(趋近)目标值为理想值时:

运用Minitab解例中的Derringer最优方程,可得最优解x*’=(0.1875, -1, 1, -0.8588),综合渴望度(1*0.667)1/2=0.817。由图2可知,S最小值(波动的最小值)S*=0.561,因而最接近的D值为:D=(dy*ds*)1/2=0.848。

图2 PerMIA方法的Derringer’s解决方案
2.4 AdSEn与双响应方法的结合
双响应方法能通过实验设计生成统计模型,在该模型中作出定义,如图3所示。
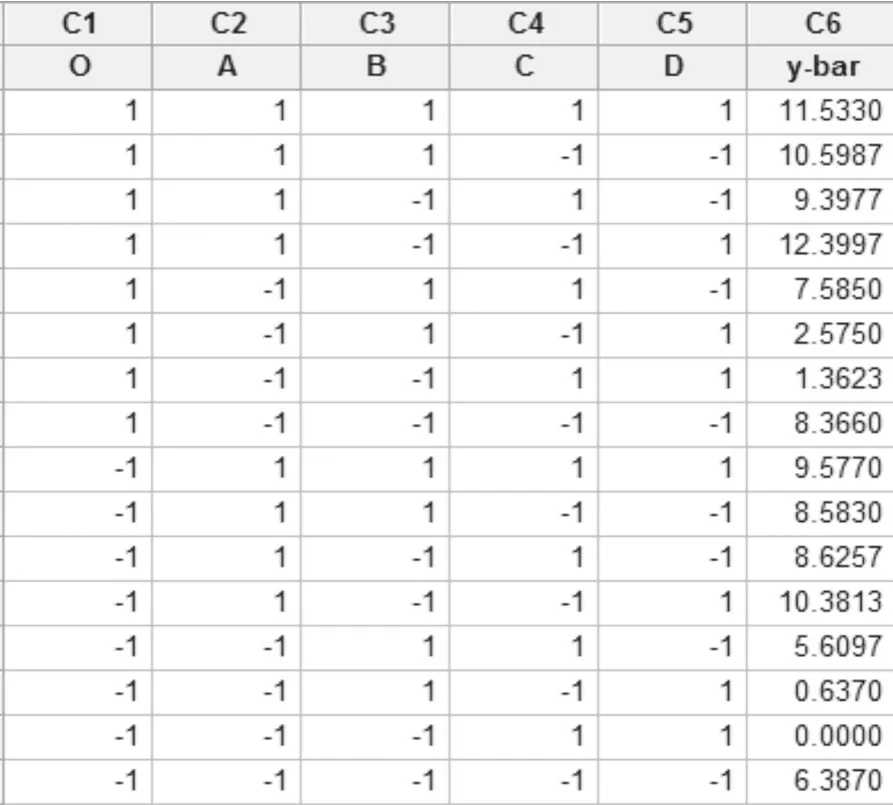
图3 双响应方法的实验设计
当去除不显著交叉因子之后,该模型可达到非常高的匹配度。通过P值可看出,影响因子B,交叉因子OA, OD, AB, AC对响应y的影响较低;交叉因子OB具有相当高的P值,对模型影响较为明显。因此,选取B为主要影响因子,并删除模型中的OA, OD, AB,AC交叉因子。同时,DB与CD交叉因子的影响也非常小。
通过对y-均值的回归系数估值(见表5)可得出如下结论:
响应面模型:

y-均值的ANOVA分析见表6。
通过上述模型可列出如下两条目标方程:

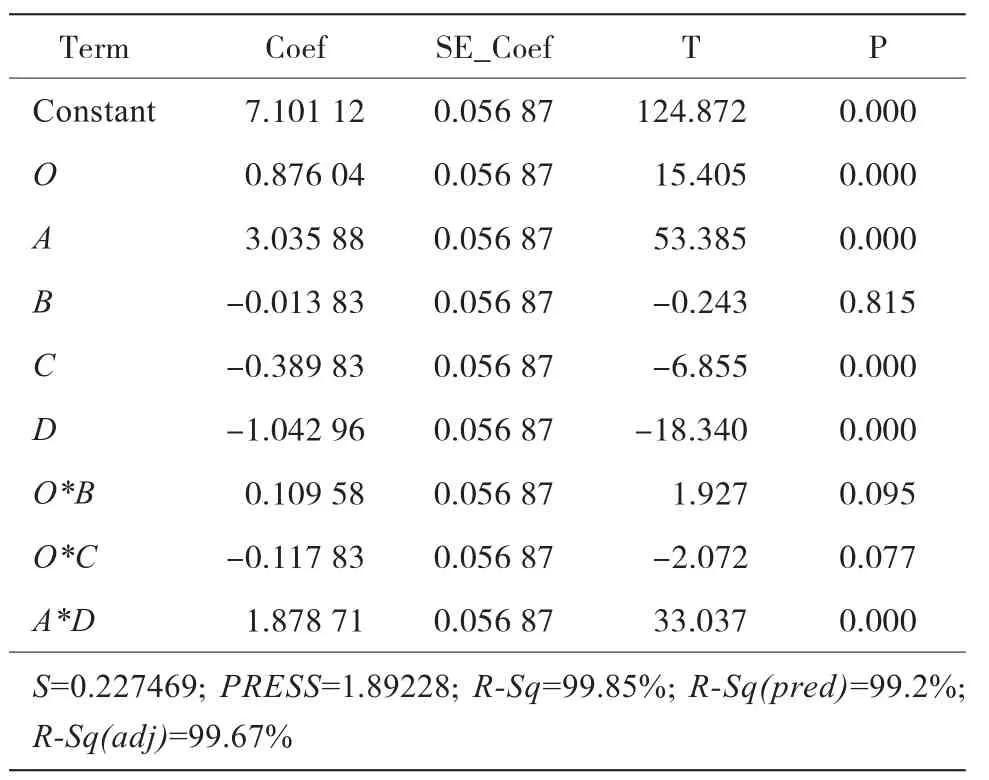
表5 y-均值的回归系数估值
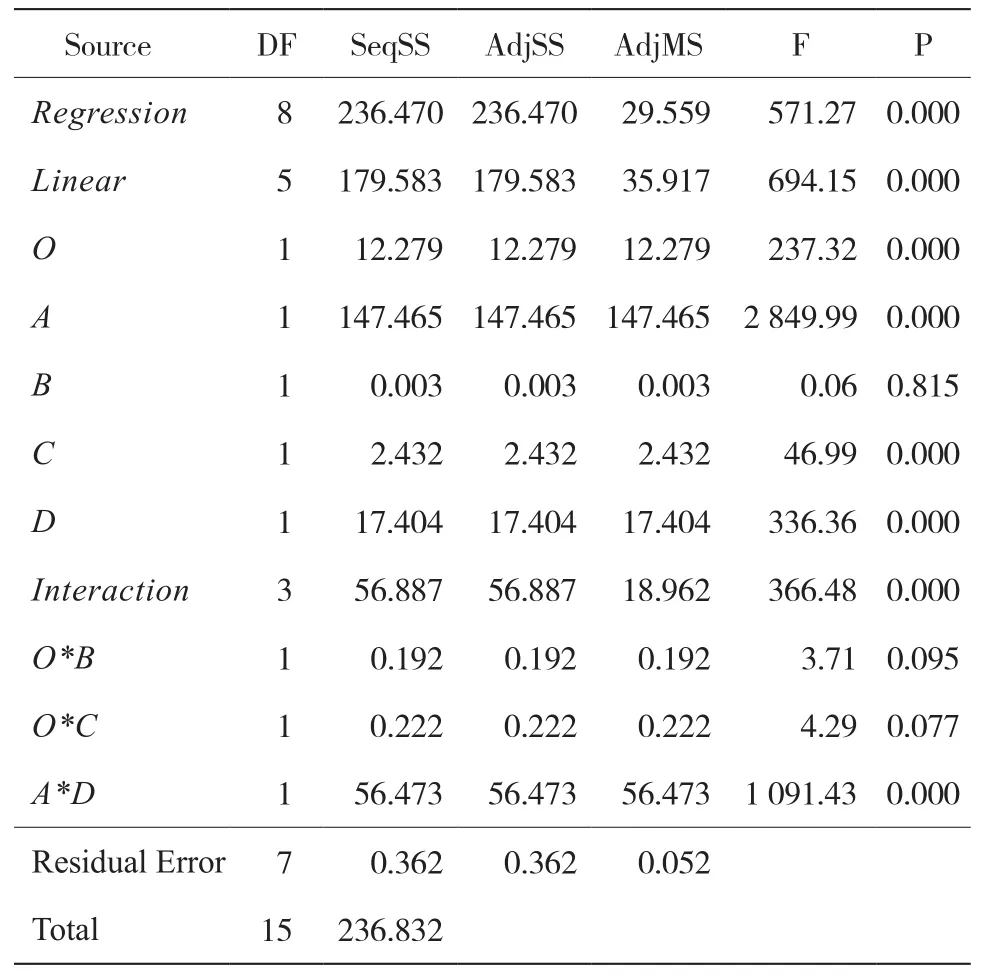
表6 y-均值的ANOVA分析
将上述两条方程联列为线性规划求最小值模型,以变化波动最小化为目标,以期望值=m的目标函数为限制条件的公式:

通过二进制搜索法,设噪声O=0,期望值m=7至9(上下限),然后进行搜索,其搜索结果如图4所示。由图4可看出,当目标噪声变量O=0时,理想结果收敛,m=8.8875时,最接近于8,如图4b所示。其对应的实验参数设计为:(A, B, C, D)=(0.44475, -1, 1,-0.29385)。
用同样的方法测试噪声因子O=[-1, 1],即非编码变量130~170,当m=8.875时,其期望响应仍在目标范围值内。因此,运用双响应模型控制的变化因素非常稳定,可将O确定在一个非常小的值上。然而,这种方法需要牺牲目标值m的精确性。当m=8.875时,偏离了目标指标8。若在设计区间内,可接受这个结论;若不在设计区间内,这种方法不可取。双响应方法的主要控制手段在于,利用m的值作为可调节的限制条件,以期获得最小的O。其模拟结果如图5所示。
2.5 结果比较
PerMIA方法、Derringer方法和双响应方法三种方法均采用编码式变量的测试方法,检验三种实验设计方案。Derringer方法与PerMIA方法类似,均分列均值和方差为不同方程;双响应方法则采用预测模型对噪声变量求偏导,由于其采用16次实验,仅为另外二者交叉数列方式的48次实验次数的1/3。通过对以上三种方法结果进行定量比较分析可看出,Derringer方法所得结果在目标值下,对噪声的抵抗力最强,其箱型图的25个百分点至75个百分点的区间最窄;双响应方法可使结果更准确地靠近设计目标,但变量非常大;只有PerMIA方法的结果在8附近,且分布较窄,如图6所示。

图4 二进制搜索法寻找最适合的组合

图5 8.75, 8.875, 9的箱型图

图6 三种方法仿真结果的箱型图
由仿真结果可看出,若以期望值为目标,双响应方法不但效果较好,且最节约成本。但双响应方法的结果分布较散,方差巨大,稳定性极弱,且AdSEn算法的基础需要大量的数据,因而与AdSEn结合时,双响应方法并不能完全发挥其优势。反之,若以最小变量为目的确定实验参数配置时,Derringer方法为最优选项。但Derringer方法对期望值的控制能力较弱,偏差较大。AdSEn算法中,其检测期望值偏差的能力远远强于检测方差波动的能力,若与Derringer方法结合,相当于把AdSEn的强项作为一个限制条件,并不能完全发挥AdSEn算法本身的作用。PerMIA方法虽然不如Derringer方法精确,且比双响应方法更昂贵,但PerMIA方法对期望值和方差的控制都较为准确。通过最直观的实验参数与实验结果的关系的展示,PerMIA方法能通过调整参数快速作出响应,并提供最优解。
3 结 论
AdSEn算法本身拥有较高响应精度,能根据阈值的设置,调节响应敏锐度,与PerMIA方法非常相似,契合度极高。但AdSEn算法的量化水平不高,而PerMIA方法本身的检测精度也有限,因而在矫正应用的实践过程中仍需探索提高目标精度的方法。PerMIA方法与AdSEn的契合将是下一步研究方向,即在保障AdSEn方法高灵敏度的情况下,探索挖掘提高PerMIA与AdSEn结合的检测精度。AdSEn方法需要大量的历史数据作为支撑,在当前生产工具高度自动化、智能化的趋势下,二进制搜索方法将变得越来越简单。通过递进算法,当将实验目标设置为m的时候,计算机能快速计算出实验结果可能的最小波动范围。但当运用于生产实践中,随着数据的积累,PerMIA方法与AdSEn的契合可从实际生产数据中进行数据挖掘,运用深度学习,最终提高控制精度,实现精确质量控制的目标,成为最契合大数据的、新一代的过程能力控制解决方案。
