HPM视角下的余弦定理教学案例
2018-07-30孔祥文
孔祥文 李 岚
数学史展现了不同方法的成败得失,今人可以从中汲取思想养料,少走弯路,获取最佳的教学方法。所以,如何将数学史融入数学教学,已经成为中学数学教师日益关注的一个课题,也是HPM(数学史与数学关系)研究领域的一个重要方向。下面就以HPM视角下余弦定理的设计和实施为例,阐述HPM视角下数学教学的设计方法,帮助学生理解数学和数学活动的本质,加强学生的学习动机。
一、教学目标
知识与技能:通过对任意三角形边长和角度关系的探索,掌握余弦定理的内容及其证明方法;能运用余弦定理解决一些简单的解三角形问题。
过程与方法:让学生从已有的几何知识出发,探究在任意三角形中,边与其对角的关系,引导学生通过观察、推导、比较,归纳出余弦定理,并对定理的证明进行实践操作。
情感态度价值观:在HPM视域下,引导学生体验知识的形成过程,提高学生发现数学规律的能力。
二、教学重点和难点
教学重点:余弦定理的探索和证明。
教学难点:余弦定理的应用。
三、教学过程
1.导入
上次课中我们学习了正弦定理,正弦定理的内容是什么?正弦定理解决了哪两类问题?如果知道两边和它们的夹角计算另一边和另两个角的问题,正弦定理还能够解决吗?这就是我们今天要学习的余弦定理。
2.新课讲解
下面我们来看如何用两边和它们的夹角计算另一边和另两个角的问题,由于涉及边长问题,我们是否可以考虑用向量的数量积,或用解析几何中的两点间距离公式来研究这个问题呢?
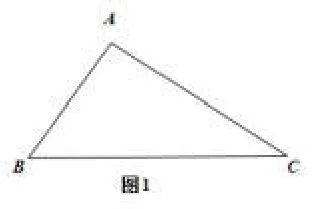
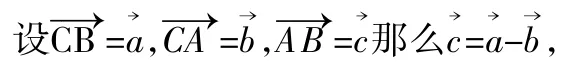

同理可证明:a2=b2+c2-2bccosA,b2=c2+a2-2cacosB.
得出如下结论:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍。即a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC。
余弦定理是作为勾股定理的推广而诞生的,公元前3世纪,欧几里得在《几何原体》第2卷分别给出钝角三角形和锐角三角形三边之间的关系(Heath,1968,403-409):
命题II.12:在钝角三角形中,钝角对边上的正方形面积大于两锐角对边上的正方形面积之和,其差为一矩形的两倍,该矩形由一锐角的对边和从该锐角(顶点)向对边延长线作垂线,垂足到原锐角(顶点)之间的一段所构成。
命题II.13:在锐角三角形中,锐角对边上的正方形面积小于该锐角两边上的正方形面积之和,其差为一矩形的两倍,该矩形由另一锐角的对边和从该锐角(顶点)向对边作垂线,垂足到原锐角(顶点)之间的一段所构成。
命题II.12.相当于说,在图2所示钝角三角形∨ABC中,
a2=b2+c2+2cm(a为钝角对边)。
命题II.13.相当于说,在图3所示锐角三角形∨ABC中,
a2=b2+c2-2cm(a为锐角对边)。其中等式(2)对于钝角三角形中的锐角对边也是成立的。

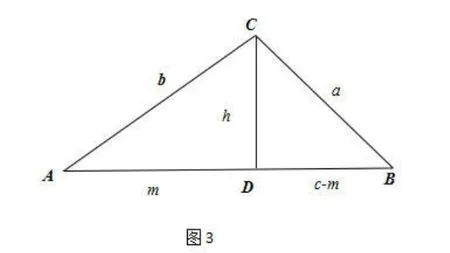
欧几里得利用勾股定理对上述命题进行证明。如图2和3所示,由勾股定理分别得:a2=h2+(c+m)2=h2+m2+c2=2cm=b2+c2+2cm,a2=h2+(c+m)2=h2+m2+c2=2cm=b2+c2-2cm。
第一种情形,m=-bcosA,第二种情形,m=bcosA,代入相应等式,即得我们熟悉的三角形式的余弦定理:a2=b2+c2-2bccosA。
教师应该注意创设情境,从具体事实出发,为学生展示数学知识的发现过程,使学生能够从中发现问题、提出问题,经历数学的发现和创造过程,了解知识的来龙去脉。实践表明,采用HPM的余弦定理教学案例,能有效激发学生的学习兴趣,得到了学生的普遍认同。
