针式翅片圆筒散热器的自然对流散热研究*

李 斌 熊 伦 唐瑜梅 涂 朴1,

(1.四川文理学院达州智能制造产业技术研究院，四川 达州 635000； 2.四川文理学院智能制造学院，四川 达州 635000)

LED(light emitting diode)是发光二极管的简称，由于其出色的电光转换效率, 被认为是即将普及的第四代照明光源[1]. 为达到更高的光照强度, LED芯片的集成密度越来越高，随之而来的是芯片热流密度快速上升, 严重影响了LED元件的发光性能和使用寿命, 为大功率照明LED的普及带来了障碍. LED以自然对流散热为主是因为其拥有换热效率高、简单和便宜的特点. 由于灯具的设计不同, 自然对流散热器的种类也随之变化. 根据翅片的种类划分,常用的散热器可划分为平板翅片式和针形翅片式. 根据翅片分布方向划分, 常用的散热器可划分为方形式和圆形式.

圆形式散热器是最近几年的研究热点. Li等[2]研究了中部有圆环的圆形散热器, 该散热器的热源位于基板底部, 对平板翅片进行了参数分析. Daeseok Jang等[3]在自然对流条件下对热源位于基板底部的针形翅片散热器进行了最优化设计.他们的研究结果表明,针形翅片平行分布的散热器在热性能上与平板翅片散热器相当，但是在重量上比平板翅片散热器轻了30%．如果对针形翅片进行错位排列,其热性能更好. Yu等[4]进行了CFD(computational fluid dynamics)建模，通过数值计算对三种板式翅片不同分布的散热器进行了热性能比较. Seung-Jae Park等[5]提出了新型的圆形散热器, 对散热器的翅片以及散热器本身的安装角度进行了分析, 并发现方向性对散热器的热性能有着显著的影响. 前述的圆形散热器研究都是基于热源位于基板底部或者翅片中间的圆环面. 而Joo等[6]研究了热源位于外部, 翅片位于内部型圆筒散热器, 对该类型散热器的平板翅片进行了最优化设计, 给出了最优化方程.

翅片位于内部型圆筒散热器能有效地提高换热效率.Joo等在设计圆筒型散热器的时候只考虑了平板式翅片, 并没有考虑针形翅片. 针形翅片在满足散热要求的情况下可以减轻LED灯具的整体重量. 因此本文基于计算流体力学(CFD)方法，对针形翅片散热器进行了仿真分析并对比了同样条件下针形翅片散热器与平板翅片散热器的热性能. 研究了针形翅片的高度对散热器散热的影响，讨论了翅片个数对散热器整体重量的影响.

符号表Nomenclature

Q：热源功率，W

ε：发射率，无量纲

N: 翅片在竖直方向的个数，无量纲

k：散热器的导热系数，W/(m·K)

L：翅片的长度，mm

H：高度，mm

t：翅片的厚度，mm

D: 散热器的直径，mm

T：温度，K

脚标subscripts

max：最大的 (maximum)

o：外部 (outer)

f：散热器翅片(fin)

i：内部 (inner)

plate：平板式

pin：针形

al：铝合金

1 散热器模型建立

翅片内分布的圆筒散热器由圆筒和翅片两部分组成. 本文以平板翅片和针形翅片两种类型作为研究对象．图1为平板翅片散热器，图2为针形翅片散热器.

图1 平板翅片散热器((a)散热器结构图；(b)平板翅片放大图)

图1(a)和图2(a)为两种散热器的整体结构图, 散热器的高度H为80 mm，圆筒的内直径Di为50 mm，圆筒的外直径Do为60 mm. 图1(b)为平板翅片的放大图, 翅片的高度与散热器的高度保持一致, 长度L为10 mm，翅片厚度t为2 mm. 图2(b)为针形翅片的放大图， 每个针形翅片的高度为Hf为2 mm，长度为10 mm，厚度为2 mm. 两种散热器的材质均采用市场上广泛应用的6061-T6型铝合金. 其密度为2 700 kg/m2，热传导率k为167 W/(m·K)，比热为896 J/(kg·K)，散热器的表面辐射发射率为0.8.

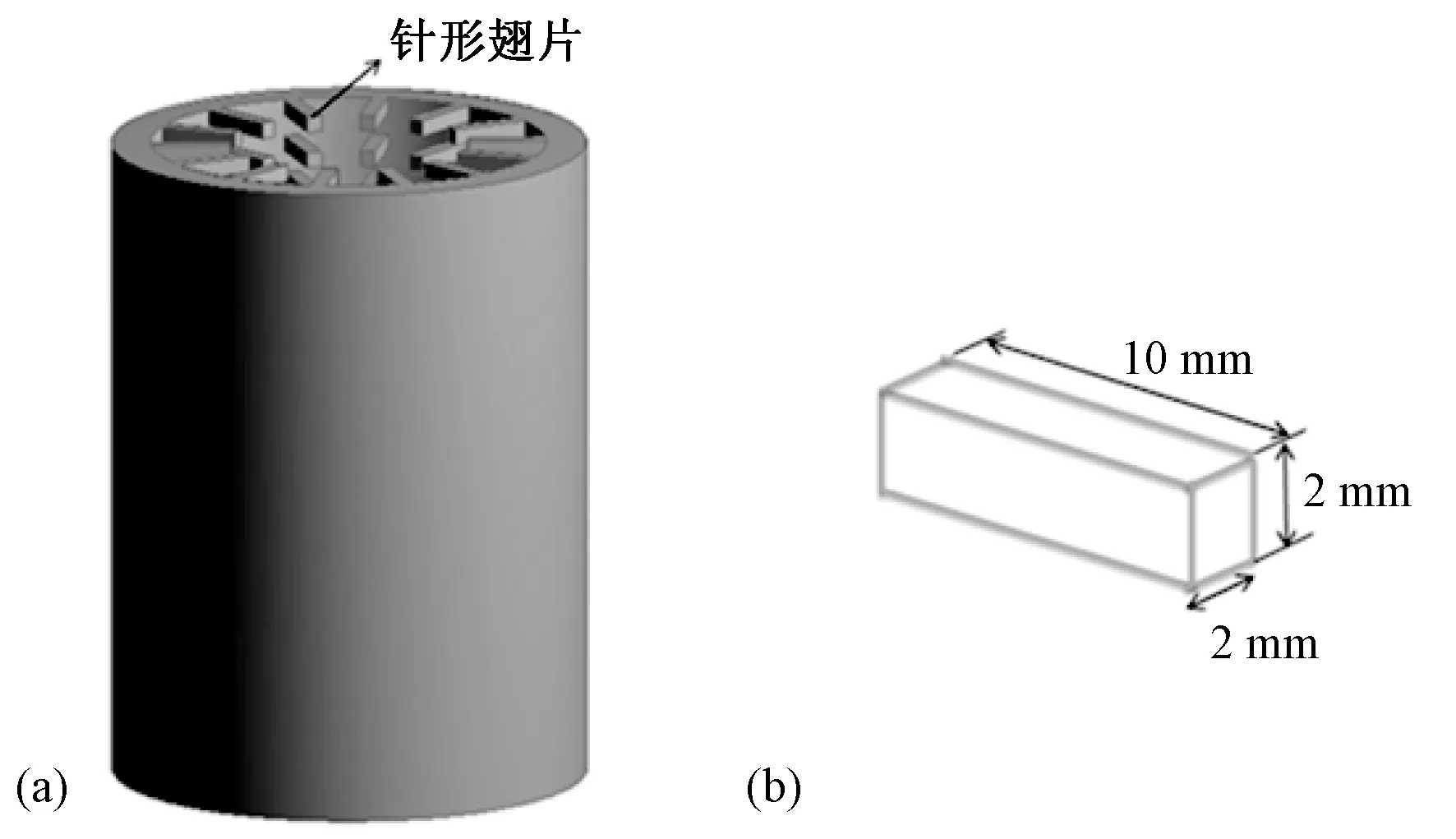
图2 针形翅片散热器((a)散热器结构图；(b)针形翅片放大图)

2 数值仿真模拟

本文对散热器进行3D建模后，采用有限体积法(FVM)进行自然对流分析. 为了确保求解域的大小对仿真结果无影响, 求解域的体积被设置为散热器整体体积的5倍. 采用HD网格器进行网格划分, 网格数由57 621到32 584区间进行网格测试, 最终选择温度没有变化时的最小网格数进行求解. 模拟自然对流散热, 求解域的顶部及四周设置为opening, 底部模拟地面而设置为wall. 在圆筒外部附上热源, 对散热器进行均匀地加热, 热源功率取值范围为5～20 W. 热源外部由胶木材质覆盖, 模拟绝热条件. 圆筒的竖直方向由上而下为重力方向, 求解域内空气温度设置为20 ℃. 本次研究用翅片的总高度与散热器高度的比例系数φ来表示翅片在竖直方向占有的比例:

(1)

其中，N为针形翅片竖直方向的排列个数，Hf为单个针形翅片的高度，H为散热器圆筒的高度. 表1陈列了针形翅片散热器在竖直方向的排列个数N的范围为：12～30. 当φ=1时,NHf为80 mm,即为平板式翅片散热器.仿真模拟中涉及到的控制方程如下：

连续方程：

(2)

动量方程：

2u,

(3)

(4)

(5)

能源方程：

2T+S,

(6)

其中能源方程中的S是辐射散热量, 采用离散坐标法对其进行计算[8].

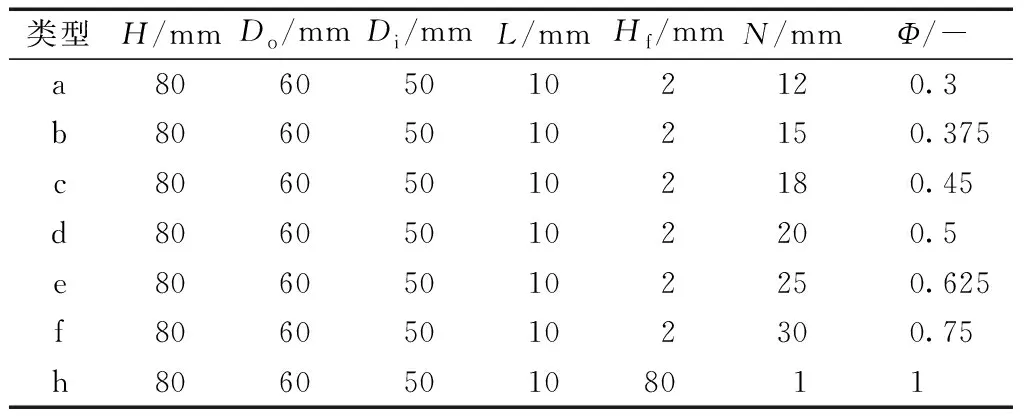
表1 各散热器翅片高度与散热器总高度的比例系数

3 结果分析

图3给出了平板式翅片散热器在功率为20 W条件下的温度分布图. 由图可见， 圆筒型散热器上面部分的温度高于下面部分的温度：由上而下, 温度逐渐降低. 图4给出了造成该现象的合理解释. 因为在翅片外部附加一个圆筒可形成“烟囱效应”[7], “烟囱”下面部分的空气流动速度比上面部分大, 此圆筒型散热器正好具有该特点. 图4(a)为N=20的针形翅片散热器速度场分布图, 图4(b)为N=5的针形翅片散热器速度场分布图. 由两个速度场分布图可知, 竖直方向针形翅片个数越多, 圆筒内部空气流动速度越大.

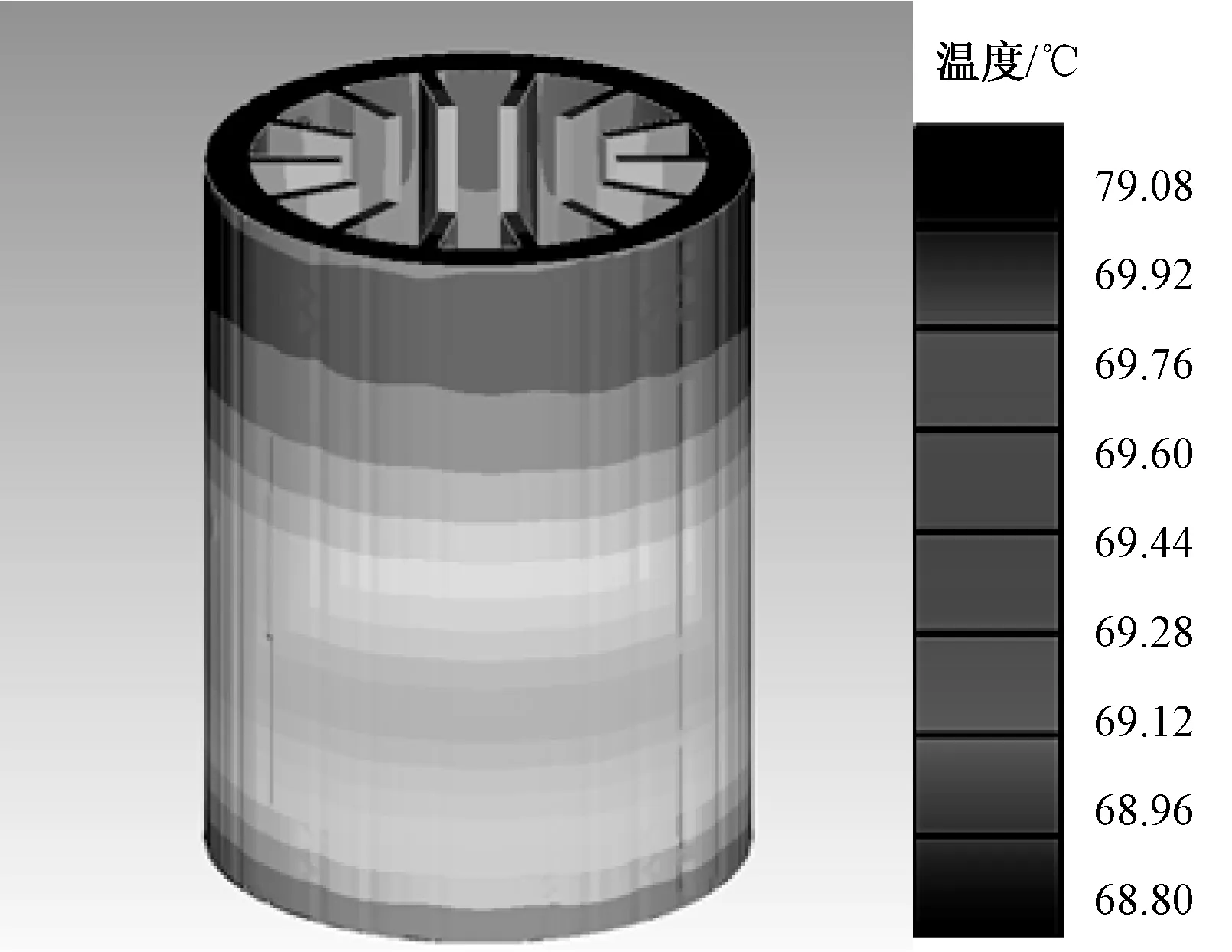
图3 平板式翅片散热器在功率为20 W条件下的温度分布图

图4 散热器内部空气流动的速度分布图((a)N=20；(b)N=5)

图5给出了不同功率下板式翅片散热器和针形翅片散热器(N=30)最高温度曲线图.由图可见, 两种散热器的温度曲线走势基本一致, 散热器的最高温度随功率的增加而增加.由此可知, 竖直方向针形翅片个数较多的散热器与平板翅片散热器的热性能相近. 图6给出了在功率为20 W的固定条件下散热器最高温度随比例系数的变化图. 通过仿真的数据可以发现, 散热器的最高温度随比例系数的增加而降低. 针形翅片个数越多, 散热器的最高温度越小. 这是因为圆筒内自然对流散热面积越大, 空气流动的速度越大，从而带走的热量越多. 这个结论与图4显示的结果一致. 然而0.625≤φ≤1.0时, 散热器的温度曲线走势趋于水平. 由此可知, 该阶段下的散热器温度变化不显著. 当φ为0.625时, 由公式(1)可得知N为25. 针形翅片的质量与平板式翅片的质量比例系数由θ来表示, 如下：

(7)

这里的V为体积,ρ为密度. 当高度比例系数φ为0.625时,N为25. 可计算得出此时针形翅片的总质量为板式翅片总质量的62.5%, 减少量为37.5%.

图5 平板翅片散热器和针型翅片散热器的温度曲线图

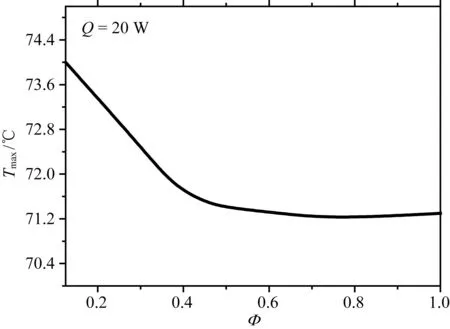
图6 不同高度比例系数下最高温度曲线图

4 结 论

通过对两种散热器进行建模和自然对流条件下的仿真研究, 可得到以下结论：

(1)竖直方向针形翅片个数过少时, 圆筒内空气流动速度减弱.

(2)数值方向个数较多的针形翅片散热器温度曲线走势与板式翅片散热器的基本一致.

(3)比例系数大于等于0.625时两种类型翅片的散热器在热性能上没有显著的区别; 比例系数小于0.625时平板式翅片散热器优胜于针形翅片散热器.

(4)比较两种散热器, 比例系数为0.625时为最优. 此时, 翅片的总重量减少37.5%.

本文选定的研究对象是一款具有代表性的圆筒形LED灯散热器,采用的研究方法和所得的数据具有可靠性、适用性，为LED灯同种产品的散热设计提供有力的参考.