交集问题特征对其解法迁移的影响

2018-07-28张令伟连四清刘芳芳尹凤艳

首都师范大学学报（自然科学版） 2018年3期

张令伟连四清刘芳芳尹凤艳

(1．首都师范大学数学科学学院，北京 100048； 2．河北省平乡县第一中学，河北平乡 054500； 3.河北省唐山市滦县第二中学，河北滦县 063700)

1 问题提出

样例在原理学习与迁移过程的作用，已经有大量的研究.在Gentner的类比结构映射理论中，样例为学习者解决新问题提供了一个类比源，类比主要是对两种情境所蕴含的结构和等级关系进行映射，只映射共同的内在关系而不包括具体事物的属性[1].

样例的表面内容对于新手解决问题的影响已有大量的研究.Gick，Reed以及Holyoak和Koh等对样例的表面内容对问题的解决迁移影响做了系列研究，研究指出样例的表面内容只对信息提取有影响，尤其是对信息的自发提取，一旦提取成功或找到合适的类比源后，接下来的应用或者映射过程将不受表面内容的影响，而只是对问题的结构信息敏感[2-4].

样例的表面内容对已经形成原理图式的熟练者问题解决影响也有一些研究.Hinsley以熟练者为被试的研究结果显示：问题的内部结构对熟悉者解决问题发生作用[5].Chi等人的研究发现，熟练者是使用问题的结构性信息来通达相关的知识，而初学者主要依靠的是表面内容.同时，Chi等人研究还发现专家的图式中也包括表面信息.这一结果表明即使问题图式概括的很好，专家在解决问题时仍需利用一些特定问题信息[6].

Blessing和Ross在对熟练者解决适宜题与不适宜问题的研究过程中，运用出声思维的方法，探讨了问题表面内容对熟练者问题解决的影响，实验设计了三类代数文字题作为研究材料，研究结果表明：熟练者在解决问题时也受到问题表面内容的影响，问题的表面内容与内部结构相适宜情况下对问题的归类或解决的成绩显著优于问题的表面内容与内部结构不适宜情况下的成绩.Blessing研究表明，熟练者的原理图式中仍然包括了具体内容信息，这些具体内容信息会影响他们对问题的解决[7].莫雷在Blessing与Ross的研究基础上运用发声思维的方法，进一步探讨表面内容的相似性对熟悉者问题归类与问题解决的影响.样例与测题的表面概貌在事件类型方面有变化的情况下，探讨了表面概貌的变化对原理运用的影响[8].

有研究证实在原理学习过程中，学习样例的表面内容不仅影响新手对问题的解决，而且也会影响已经掌握了原理的熟练者对问题的解决，这种影响作用将随着样例学习而形成的问题原型概括化程度的提高而逐步减弱[9].

张令伟，连四清，尹凤艳等以高中三个年级已学习过交集知识的学生为被试，进一步研究了样例与新问题的表面内容的相似性对迁移的影响，结果表明：对于熟悉学者来说，样例和测题表面特征的不同相似关系对问题解决迁移成绩有不同的影响．应用类型表面特征的具体情节发生较大变化时，对问题解决方法的通达、提取和运用的迁移有影响；变量类型问题表面特征的具体情节发生较大变化时，不仅对问题解决方法的通达有影响，而且对方法的提取和运用也有影响；当被试学生年级类型不同时，影响也不同[10]．

张令伟等人以高中三个年级已学过交集知识的学生作为被试，应用类型和变量类型为变量，研究样例与新问题的表面内容的相似性对迁移成绩的影响，但是三个年级中学生类型不同时实验结果是否会与已有结果一致，还没有进一步的研究.本文设想：以高中三个不同年级都已学过交集知识的学生作为被试，以测试题的迁移水平和学生类型为研究变量，研究样例与新问题的表面内容的相似性对迁移成绩的影响，以便为不同年级不同类型的学生交集教学设计提供理论上的依据.

2 研究方法

实验设计：本实验采用3(年级：高中一、二、三年级)×3(学生类型：学优生、学中生、学差生)×7(迁移水平：七个不同的迁移水平)三因素混合设计，迁移水平为被试内变量，年级、学生类型为被试间变量.其中，年级是指高中一年级、高中二年级，高中三年级；学生类型是指把每个参加问卷调查的班级按照上学年的期末考试成绩分别分为学优生、学中生、学差生；迁移水平是指七道测试题，每一题为一个迁移水平.研究变量为迁移成绩.

被试：选择唐山市某中学的高一、二、三年级各个班的学生作为被试，每一个班均为普通班，高中一年级55名，高中二年级49名，高中三年级27名，共131名学生被试.根据各班的上学期期末考成绩将每个班的学生分为学优生、学中生、学差生三个类型.分类的依据是：期末考成绩的平均分加减标准差.在实验过程中有学生没有按要求进行实验，如测试卷上不写姓名，或迁移成绩与月考成绩出入很大，这些学生被试的数据在统计分析时被剔除.最后有125名学生被试的数据有效，高中一年级53名，高中二年级45名，高中三年级27名.

实验材料：实验材料包括学习材料和测试材料.学习材料由一个交集的概念和一道学习样例题组成.学习样例给出了样例的解答过程.测试材料由7道测试题组成，分为四类题目.第一类，测试题与样例的表面概貌相似，表面对应相似；第二类，测试题与样例的表面概貌不相似，表面对应相似；第三类，测试题与样例的表面概貌不相似，表面对应相似；第四类，测试题与样例的表面概貌不相似，表面对应相似. 为了消除顺序效应，本实验的测试材料采用拉丁方设计，共有7套测试卷.高中三个年级学习材料和测试材料试卷都相同.

实验程序：首先让被试用10分钟时间阅读学习材料.然后向被试发放学习材料，20分钟后统一收回测试材料.

数据的观测方法：按满分10分的评分标准对被试答卷进行评分，每道题结果全对给10分；第五题没有舍去1的给8分，只写出0的给1分；写出0和正负值中一个的给4分；第六题缺等号的给5分；第七题写对一个给5分.

3 实验结果

三个年级实验研究中，交集问题特征对七种不同迁移水平的问题解决迁移成绩描述性统计结果如表1和表2.

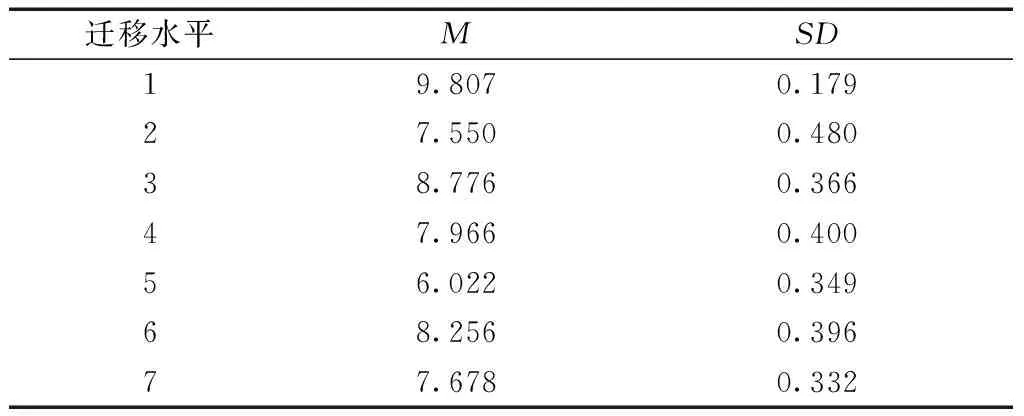
表1 交集问题七种迁移水平问题解决迁移成绩描述统计表

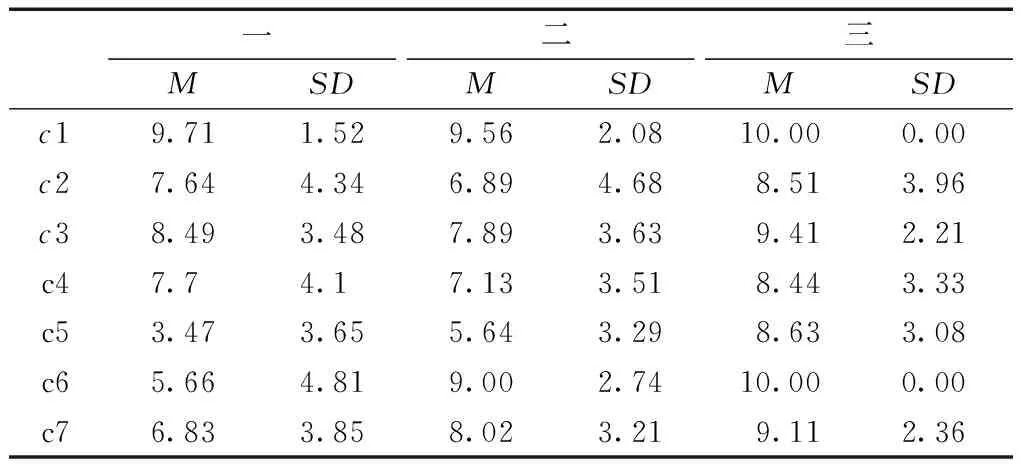
表2 高中三个年级七个迁移水平问题解决迁移成绩描述统计表

从表1可以看出,三个年级七种迁移水平上,迁移成绩有显著差异, 七种迁移水平成绩平均分从高到低依次是: 迁移水平1>迁移水平3>迁移水平6>迁移水平4>迁移水平7>迁移水平2>迁移水平5.

表2是迁移成绩平均分和标准差的描述性统计结果，期中c表示迁移水平.从表2可以看出，年级类型对交集的问题解决迁移成绩有显著影响，不同年级在七种迁移水平上有不同的差异；对于高中一年级学生来说，七种迁移水平成绩平均分从高到低依次是：迁移水平1(9.91)>迁移水平3(8.49)>迁移水平4(7.70)>迁移水平2(7.64)>迁移水平7(6.83)>迁移水平6(5.66)>迁移水平5(3.47)；对于高中二年级学生来说，七种迁移水平成绩平均分从高到低依次是：迁移水平1(9.56)>迁移水平6(9.00)>迁移水平7(8.02)>迁移水平3(7.89)>迁移水平4(7.13)>迁移水平2(6.89)>迁移水平5(5.64)；对于高中三年级学生来说，七种迁移水平成绩平均分从高到低依次是：迁移水平1(10.00)=迁移水平6(10.00)>迁移水平3(9.41)>迁移水平7(9.11)>迁移水平5(8.63)>迁移水平2(8.51)>迁移水平4(8.44).

对高中三个年级交集问题解决的迁移成绩进行3(年级：高中一、二、三年级)×3(学生类型：学优生、学中生、学差生)×7(迁移水平：七个不同的迁移水平)重复测量方差统计，结果如下：表3是高中三个年级交集问题解决的迁移成绩方差分析结果，表4是交集问题特征对不同学生类型和不同年级迁移成绩方差分析结果.

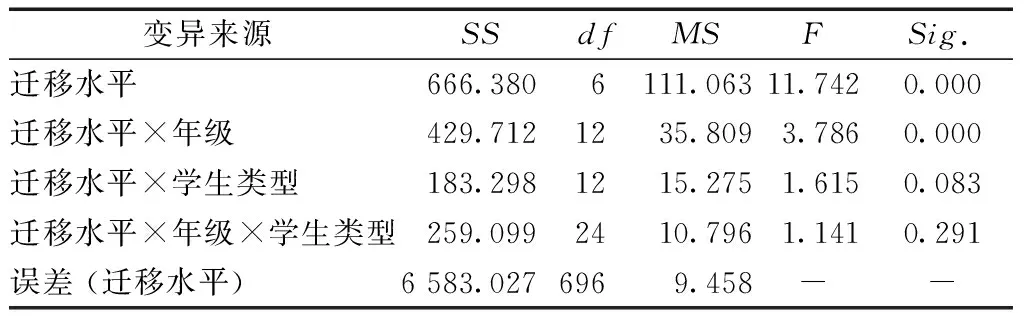
表3 高中三个年级交集平问题解决迁移成绩方差分析表

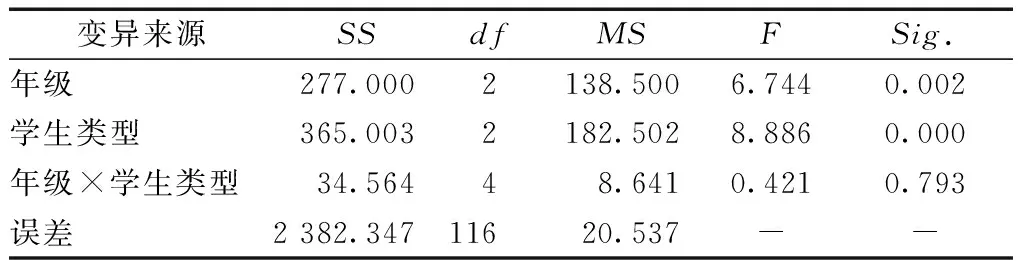
表4 交集问题特征对不同学生类型和不同年级迁移成绩方差分析表

表3结果表明：迁移水平的主效应极其显著(F=11.742，P=0.000)，迁移水平与年级类型交互效应极其显著(F=3.786，P=0.000).这说明迁移水平主效应存在年级类型差异.迁移水平与学生类型交互效应边际显著(F=1.615，P=0.083).这说明迁移水平对迁移成绩的影响存在一定的学生类型差异.迁移水平、年级类型与学生类型三因素交互效应不显著(F=1.141，P=0.291>0.05).这说明迁移水平与学生类型交互效应不存在年级类型差异.

进一步对迁移水平类型因素在年级类型的三个水平上做简单效应检验结果知：在高中一年级水平上F=18.268，P=0.000；在高中二年级学生水平上F=8.151，P=0.000；在高中三年级学生水平上F=0.025，P=0.875.这说明对于高中一年级学生来说，迁移水平因素对问题解决的迁移成绩有极其显著的影响；对于高中二年级的学生来说，迁移水平因素对问题解决的迁移成绩也有极其显著影响；对于高中高三年级的学生来说，迁移水平因素对问题解决的迁移成绩没有显著影响，与高中二年级学生比较而言，对高中一年级学生的影响更大.迁移水平与年级类型交互作用图如下图.

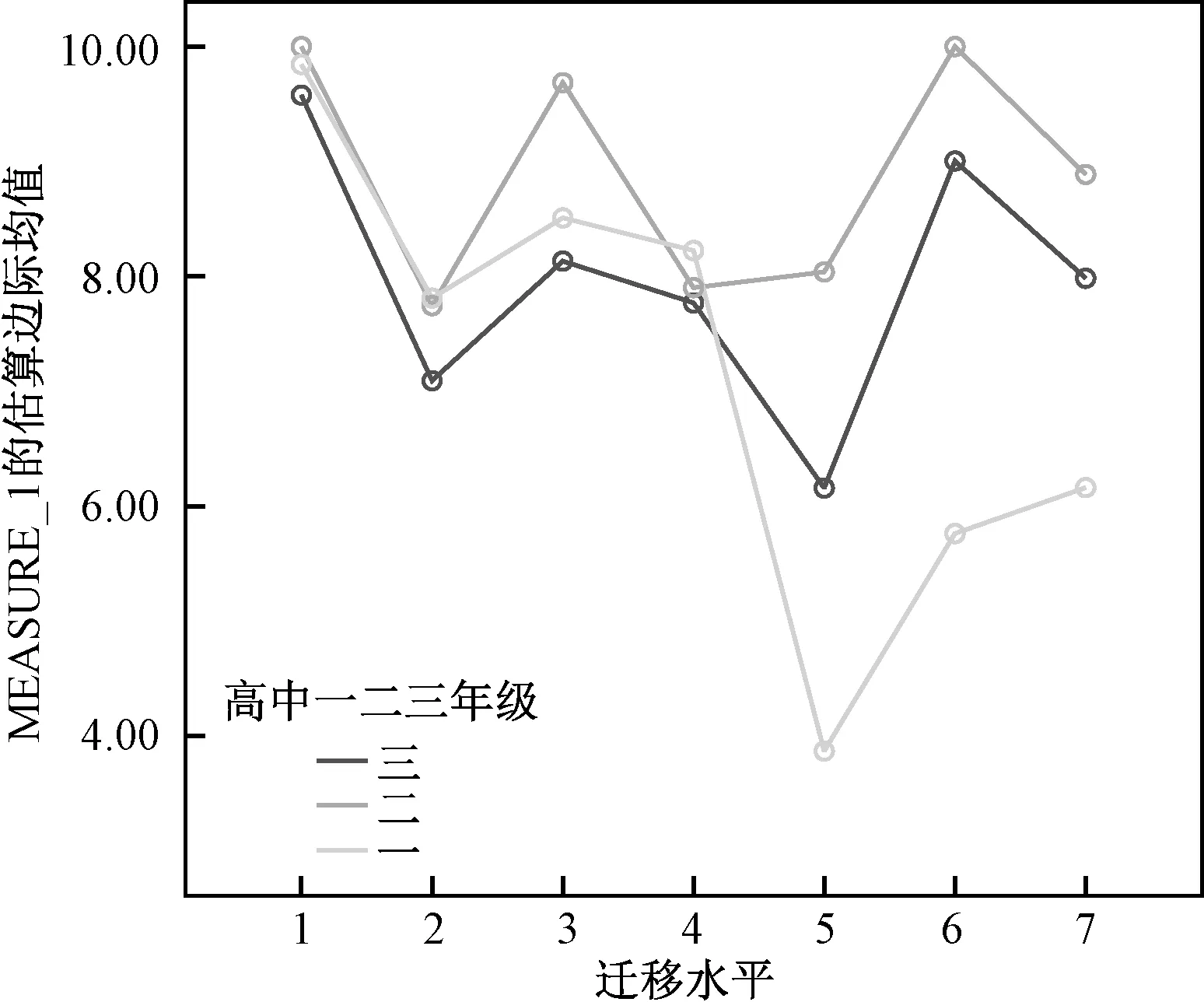
表4结果表明：年级类型的主效应显著(F=6.744，P=0.002<0.01)，这说明年级类型因素对迁移成绩影响非常显著.学生类型的主效应显著(F=8.886，P=0.000<0.01)，这说明学生类型因素对迁移成绩影响极其显著.年级类型与学生类型交互效应不显著(F=0.421，P=0.793>0.05)，这说明年级类型对迁移成绩的影响不存在的学生类型差异.

对于年级类型来说，高中一年级学生与高中二年级学生迁移成绩存在边际差异(P=0.06)，高中一年级比高中二年级学生迁移成绩平均分低0.660 6分；高中一年级学生与高中三年级学生迁移成绩存在极其显著差异(P=0.000)，高中一年级学生比高中三年级学生迁移成绩平均分低2.033 0分；高中二年级学生与高中三年级学生迁移成绩存在十分显著差异(P=0.001)，高中二年级学生比高中三年级学生迁移成绩平均分低1.372 5分.

4 分析与讨论

本实验的目的：探讨高中三个年级不同类型的学生(都已经学习过交集的有关知识)作为被试时，样例与测题的问题特征相似性对问题解决的迁移成绩的影响.实验的基本设想是：不同迁移水平问题特征对问题解决的迁移成绩都有影响；问题特征的不同相似性对不同年级的学生问题解决的迁移成绩的影响不同；问题特征的不同相似性对不同类型的学生问题解决的迁移成绩的影响不同.

实验结果表明：迁移水平的主效应极其显著，迁移水平主效应存在学生类型差异，迁移水平主效应也存在年级类型差异，也就是说迁移水平对问题解决的迁移成绩有极其显著影响.这一结果与我们的预期基本一致同.结果说明，不同的迁移水平影响问题解决方法的通达、提取和应用.其原因一方面可能是：被试通过对样例学习及对样例和测题表面特征的比较，可能已经概括出样例与测题在不同迁移水平下它们之间所蕴涵的关系和结构，进而在解题过程中直接把这种关系映射过来.在样例和测题中，如已知条件表达式“设A={3,5,6,8}，B={4,5,7,8}”和所求表达式“A∩B”中蕴涵的隐含条件是求集合A与B的公共元素，同样在测试题中，如已知条件表达式“设A={4,5,6,8}，B={3,5,7,8}”和所求表达式“A∩B”中所蕴涵的隐含条件也是求集合A与B的公共元素.这样被试把样例中的解题方法“找公共元素”直接迁移到测题中应用；而对于形如“已知集合A={x|x≤1}，B={x|x≥a}，且A∩B={x|x≥a}，则实数a的取值范围是？”的测试题，样例的解题方法不能直接迁移应用，这就需要被试不仅利用A∩B是A与B的公共元素做成的集合，而且要从工作记忆中搜索与解题有关的信息，从而增加了学生的认知负荷.

正如我们假设的那样，对于已有经验的被试来说，年级类型的主效应十分显著，也就是说年级类型因素对迁移成绩影响非常显著.这说明年级类型因素影响解题方法的通达、提取和应用.其原因可能是：学习样例中给出的已知条件表达式如“设A={4,5,6,8}，B={3,5,7,8}”，为所求“A∩B”，问题解决过程中直接利用“求公共元素”的方法.但是测题中包含四类题：第一类，测试题与样例的表面概貌相似，表面对应相似；第二类，测试题与样例的表面概貌不相似，表面对应相似；第三类，测试题与样例的表面概貌不相似，表面对应相似；第四类，测试题与样例的表面概貌不相似，表面对应相似.这些测题与样例在表面概貌的具体情节上有些变化较大，不同年级的被试可能不同程度的揭露这种隐蔽条件，看出测题与样例表面特征的隐蔽的相似性，从而在问题解决过程中迁移完成程度也不同.

迁移水平与年级类型交互效应极其显著，这说明迁移水平对迁移成绩的影响存在一定的年级类型差异，也就是说对于不同年级类型的学生，迁移水平对迁移成绩的影响不同.进一步的简单效应分析发现：对于高中一年级学生来说，迁移水平因素对问题解决的类比迁移成绩有极其显著的影响；对于高中二年级的学生来说，迁移水平因素对问题解决的类比迁移成绩也有极其显著影响；对于高中三年级的学生来说，迁移水平因素对问题解决的类比迁移成绩没有显著影响，与高中二年级学生比较而言，对高中一年级学生的影响更大.出现这一现象的原因可能是不同年级类型的学生对解决过的问题的图式归纳方式不同，或者至少是侧重不同：高中三年级学生更善于或侧重于归纳出问题的结构特征，在解决新问题时能排除表面信息的干扰；而高中一年级学生和高中二年级学生往往不能归纳出问题的结构特征而依赖问题的表面特征，最终保存在他们长时记忆中的是关于问题的表面的、非结构的信息，他们不能揭露表面特征的隐蔽条件，看到表面特征的隐蔽的相似性.