基座运动对并联调整机构动力学性能的影响

2018-07-28姚建涛窦玉超许允斗赵永生

农业机械学报 2018年7期

姚建涛韩博窦玉超张硕许允斗赵永生

(1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛 066004；2.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛 066004；3.中国电子科技集团公司第五十四研究所，石家庄 050081)

0 引言

上海65 m射电望远镜是一台65 m口径全方位可动的大型射电天文望远镜，其天线主面直径为65 m，副面口径为6.5 m，由4根与主反射面相连的桁架支撑，距离地面70 m，为了适应多频段馈源工作要求，并补偿由重力变形或者外界风、雨、雪等因素引起天线性能和指向的变化，在副面与桁架之间装有并联调整机构，可根据天线主面工作状态对副面进行实时多自由度位姿调整[1-4]。

副反射面调整机构为典型的六自由度Stewart并联机构，并联机构动力学分为正向动力学和逆向动力学，目前研究较多的是逆向动力学，即根据并联机构动平台位姿、速度和加速度计算各分支的驱动力[5-9]。并联机构常用的动力学建模方法有牛顿欧拉法[10-11]、拉格朗日法[12-13]和Kane法[14-16]等，其中牛顿欧拉法物理意义明确、可求得系统内部约束反力，但仅适用于简单系统；拉格朗日法动力学方程形式简单、适用于复杂系统动力学建模，但过程复杂且计算量庞大；Kane法用矢量运算符叉积、点乘代替求导运算，运算速度得到极大提升，适用于实时运算，但偏速度和偏角速度概念较难理解。虽然不同的建模方法各具特点且建模过程不同，但最终得到的结果是一致的。

DO等[17]使用牛顿欧拉方法建立了Stewart平台的动力学模型，文献[18]则在系统动力学建模过程中考虑了驱动分支的惯量对系统整体动力学性能的影响，并进行了详细分析；文献[19-20]使用拉格朗日法对几种构型并联机构进行了动力学建模研究；丁华锋等[21]运用Kane方法对一种正铲液压挖掘装置进行了动力学分析；蔡赟等[22]提出了一种联合应用Kane方程及拉格朗日方程的动力学解耦方法，并对一种3PTT-2R串并联数控机床动力学耦合特性进行了研究；文献[23-25]对基座运动和负载运动情况下的并联机构动力学建模方法进行了研究分析。

上述文献多数是对基座固定情况下的并联机构动力学建模方法的研究，只有极少数学者考虑了基座运动对机构动力学性能的影响，但却忽略了控制系统对动力学模型计算的高实时性要求。本文采用Kane方法针对射电望远镜副面并联调整机构进行基座运动情况下的动力学建模与计算，分析基座运动对并联调整机构动力学性能的影响，从而为此类并联装备机械结构强度校核和控制系统参数的确定奠定理论基础。

1 并联调整机构构型介绍与位姿描述

副面并联调整机构为Stewart构型，主要由定、动平台及6条可伸缩的UPS支链构成，构型如图1所示。

该机构由基座、运动平台、连接基座和运动平台的6个驱动分支组成，其中基座与射电望远镜的桁架固连，副面安装在运动平台的底面上。驱动分支则由1个虎克铰、1个移动副以及1个球铰依次连接而成。其中虎克铰与基座相连，球铰与运动平台相连，采用移动副作为分支的驱动输入。6个虎克铰Bi(i=1，2，…，6)共分3组且均布在半径为R的圆周上，组间的夹角为φ1，组内两虎克铰间夹角为θ1。6个球铰ai(i=1，2，…，6)共分3组均布在半径为r的圆周上，组间夹角为φ2，组内两球铰间夹角为θ2。

如图1所示，为了描述动平台(副反射面)相对基座的位姿，在虎克铰分布圆的中心以及副面与运动平台组合体的质心分别建立直角坐标系{B}和{P}，其中坐标系{B}的yB轴与∠B1oBB2的角平分线重合，zB轴垂直于基座竖直向上。坐标系{P}的yP轴与∠a1oa2的角平分线平行，zP轴垂直于运动平台且过其中心o点，oP与o距离为d。副面相对基座的位姿即可用坐标系{P}在坐标系{B}的位姿进行描述，初始位姿下，xP、yP轴分别与xB、yB轴对应平行，zP轴与zB轴重合。

2 基座运动对动平台和驱动分支受力影响

在射电望远镜天线跟踪天体运动的过程中，并联调整机构的基座相对大地将产生运动，这不但增加了各构件的惯性力，同时在坐标系{B}下各构件的重力矢量方向也将发生改变。为对基座运动引起的各构件惯性力和重力矢量的变化进行分析，确定基座运动对系统动力学的影响，在天线方位和俯仰转动中心建立大地参考坐标系{W}，如图2所示。

图2 系统坐标系设置Fig.2 Coordinate system settings

(1)

式中，基座位置矢量WpB|W下角标B代表与被描述对象固连的坐标系{B}，上角标W则表示被描述对象的参考坐标系{W}，下角标W则表示在坐标系{W}下对基座的位置进行描述，其他变量角标定义以此类推。

基座在大地坐标系下的位姿为

(2)

2.1 基座运动对动平台的受力影响分析

取基座在坐标系{W}下的位姿WXB|W为其广义坐标

(3)

式(3)两端分别对时间求导，可得基座在大地坐标系{W}下的速度为

(4)

根据坐标系间速度的映射关系，基座速度在坐标系{B}下可表示为

(5)

将式(5)两端分别对时间求导，可得坐标系{B}下基座的加速度

(6)

根据速度合成定理，由基座运动引起的动平台线速度和角速度可分别表示为

(7)

WωP|B=WωB|B

(8)

将式(7)两端分别对时间求导，可得坐标系{B}下动平台的线加速度为

BpP|B+WωB|B×(WωB|B×BpP|B)

(9)

其中，式(9)中的第2项为动平台的科氏加速度，第4项为动平台的向心加速度。

根据角加速度合成定理，可得坐标系{B}下动平台的角加速度为

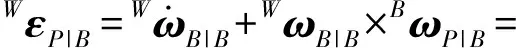
(10)

根据牛顿第二运动定律，基座运动引起的动平台惯性力为

(11)

根据牛顿欧拉方程，基座运动引起的动平台惯性矩为

MP|B=IP|BWεP|B+WωP|B×(IP|BWωP|B)=
IP|B(WεB|B+WωB|B×BωP|B)+WωP|B×(IP|BWωP|B)

(12)

式中IP|B——坐标系{B}下动平台的惯性张量

2.2 基座运动对驱动分支的受力影响

为了对基座运动引起的分支惯性力进行分析，以第i个分支为研究对象，以质心mfi和mmi为原点分别建立坐标系{Ci}和{Di}。其中坐标系{Ci}的xCi轴沿分支杆长指向动平台一侧，yCi轴垂直于轴xCi且始终与坐标系{B}的xByB平面保持平行，根据右手法则可确定zCi轴指向，且zCi轴在zB轴上的投影始终指向zB轴的正方向。同理，坐标系{Di}的xDi轴沿分支杆长指向动平台一侧，yCi轴垂直于轴xCi且始终与xByB平面保持平行，zCi轴在zB轴上的投影亦始终指向zB轴的正方向，如图3所示。

图3 驱动分支质心坐标系Fig.3 Center of mass coordinate of link

根据空间矢量合成定理，质心mfi相对坐标系{W}的位置矢量在坐标系{B}下的表示为

(13)

式(13)两端对时间求导，并根据速度合成定理，可求得质心mfi的线速度为

Wvfi|B=WvB|B+WωB|B×(BpBi|B+lfsi)

(14)

式(14)两端对时间求导可得坐标系{B}下质心mfi的线加速度为

(15)

其中第2项为质心mfi的科氏加速度，第4项为质心mfi的向心加速度。

根据牛顿第二定律，基座运动引起的基座侧驱动分支惯性力为

Fmi|B=mfWafi|B=
mf{WaB|B+2WωB|B×Bvfi|B+WεB|B×(lfisi+Bi)+
WωB|B×[WωB|B×(lfisi+Bi)]}

(16)

为了计算基座运动对驱动分支惯性矩的影响，首先确定驱动分支的惯性矩阵在坐标系{B}下的表示。根据图3中所示驱动分支质心坐标系{Ci}和{Di}的设置，可得坐标系{Ci}向坐标系{B}的映射矩阵为

(17)

已知在坐标系{Ci}下分支惯性矩阵为If|C，则其在坐标系{B}下可表示为

(18)

根据角加速度合成定理，基座运动引起的质心mfi处的角加速度为

(19)

则根据牛顿欧拉方程，基座运动引起的基座侧分支所受惯性矩为

(20)

对于运动平台侧驱动分支，其质心mmi在坐标系{B}下的位置矢量为

Wpmi|B=WpB|B+Bpmi|B

(21)

式(21)两端对时间求导，可求得质心mmi的线速度为

(22)

式(22)两端对时间求导可得质心mmi的加速度为

(23)

其中第2项为质心mmi的科氏加速度，第4项为质心mmi的向心加速度。

则由基座运动引起的运动平台侧分支惯性力为

Fmi|B=mmWami|B=
mf{WaB|B+2WωB|B×Bvmi|B+WεB|B×Bpmi|B+
WωB|B×[WωB|B×(Bi+(li-lmi)si)]}

(24)

由于驱动分支两部分间轴线始终保持重合，故坐标系{Di}向坐标系{B}的映射矩阵满足

(25)

所以，坐标系{B}下运动平台侧驱动分支惯性矩阵可以表示为

(26)

由于驱动分支两段间的角加速度始终保持相等

(27)

根据牛顿欧拉方程，基座运动引起的运动平台侧驱动分支惯性力矩为

(28)

2.3 基座运动对重力加速度方向矢量的影响

基座坐标系{B}与大地坐标系{W}间不存在相对运动的情况下，两坐标系坐标轴对应平行，此时坐标系{B}下重力加速度矢量为

(29)

(30)

3 并联调整机构动力学建模

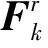
(31)

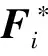
(32)

即作用于刚体简化中心上的主动力和主动力矩，分别与该点对应于某一独立速度的偏速度和偏角速度的标量积之和称为刚体对应于该独立速度的广义主动力。广义惯性力则为刚体质心上作用的惯性力和惯性力矩与该质心对应于某一独立速度的偏速度与偏角速度的标量积之和。

3.1 基座固定情况下系统动力学建模

已知动平台和副面的质量之和为mP，对于第i个驱动分支，其基座一侧质量为mf，运动平台一侧质量为m，分支驱动力为Fi，重力加速度为gB。

根据系统广义主动力的定义，可知对应于广义速率的系统广义主动力为

(33)

其中，各偏速度下角标k表示偏速度的第k列构成的向量，其中k依次取1，2，…，6。

对应于广义速率的系统广义惯性力为

(34)

其中，各偏速度下角标k表示偏速度的第k列构成的向量，其中k依次取1，2，…，6。

根据式(31)中Kane方程的定义可得并联调整机构动力学方程为

(35)

式(35)经过整理，可以表达为

(36)

式中F——各分支驱动力组成的行向量

eF——系统中对应各偏速度的广义惯性力与除广义驱动力以外的其他广义主动力之差组成的行向量

该行向量的第k个元素为

(37)

G6×6为除广义驱动力以外的广义主动力和惯性力之和向分支驱动力的映射矩阵

(38)

根据式(36)中建立的分支驱动力与除广义驱动力以外的其他广义惯性力和广义主动力之差的映射关系，即可计算出基座固定时对应指定运动参数下分支的驱动力。

3.2 基座运动情况下系统动力学建模

由前述基座运动影响下动平台和驱动分支受力分析，可知动平台和驱动分支所受惯性力和惯性力矩以及重力加速度在坐标系{B}下的表示，则基座运动情况下系统主动力和主动力矩对应于广义速率的广义主动力为

(39)

其中，各偏速度下角k表示由偏速度的第k列构成的向量，k依次取1，2，…，6。

对应于广义速率的系统广义惯性力为

(40)

根据Kane方程的定义，基座运动情况下作用在调整机构各构件上相对于广义速率的广义主动力和广义惯性力之和为零，则系统动力学方程为

(41)

式(41)经过整理，可以表示成

F′=eF′G′6×6-1=

(42)

式中eF′——系统中对应各偏速度的广义惯性力与除广义驱动力以外的其他广义主动力之差组成的行向量

该行向量的第k个元素为

(43)

G′6×6-1为系统中除广义驱动力以外的广义主动力和惯性力之和与分支驱动力间的映射矩阵，其中

(44)

根据式(42)中建立的分支驱动力与除广义驱动力以外的其他广义惯性力和广义主动力之差的映射关系，即可计算出基座运动情况下对于指定运动参数下分支的驱动力，即系统的动力学逆解。

4 并联调整机构动力学数值与仿真分析

并联调整机构结构及物理参数见表1。

运用上述理模型和机构参数，在Matlab中进行编程计算求解，得到的驱动力如图4所示。

将图4和图5所示两种情况下系统的驱动力进行对比，结果如图6所示。

表1 结构及物理参数Tab.1 Structural and physical parameters

图4 基座固定情况下分支驱动力理论值Fig.4 Theoretical value of driving force with condition of fixed base

图5 基座运动情况下分支驱动力理论值Fig.5 Theoretical value of driving force with condition of moving base

图6 基座运动对分支驱动力的影响(理论值)Fig.6 Influence of base moving on driving force (theoretical value)

为验证理论模型的正确性，采用系统动力学分析软件ADAMS对机构进行动力学仿真，将建立好的三维模型导入到ADAMS软件中，并添加相关运动副约束，设置并联调整机构的驱动模型，使其与上述规划的运动模型一致，虚拟样机模型如图7所示，仿真结果如图8～10所示。

图7 并联调整机构ADAMS模型Fig.7 ADAMS model of parallel adjusting mechanism

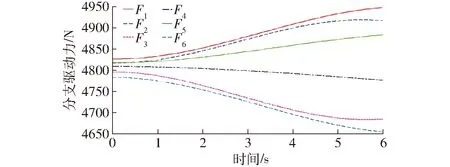
图8 基座固定情况下分支驱动力仿真值Fig.8 Simulation value of driving force with fixed base

图9 基座运动情况下分支驱动力仿真值Fig.9 Simulation value of driving force with moving base

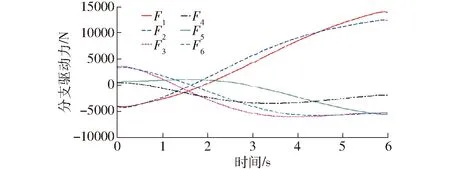
图10 基座运动对分支驱动力的影响(仿真值)Fig.10 Influence of base moving on driving force (simulation value)

对比图4～6与图8～10的仿真曲线，可以得出前述并联调整机构动力学模型的正确性。

对比图6和图10中各分支驱动力变化曲线可以得知，在基座运动的影响下，1、2分支驱动力先减小后增大，最大增幅接近14 000 N。第3、4、5、6分支驱动力则是先增大后减小，驱动力由拉力(正值)逐渐过渡为推力(负值)，最大增幅6 000 N。通过以上分析可以得知，基座运动对系统动力学性能影响是不容忽视的，在结构设计及强度校核、电机选型和控制策略设计过程中应充分考虑基座运动的影响，以提高系统参数的准确性和结构强度的可靠性。