水田电动双行深施肥除草机设计与试验
2018-07-28王金峰高观保闫东伟王金武翁武雄陈博闻
王金峰 高观保 闫东伟 王金武 翁武雄 陈博闻
(东北农业大学工程学院,哈尔滨 150030)
0 引言
水稻生长过程大致分为幼苗期、分蘖期、拔节期、孕穗期、抽穗期、扬花期、乳熟期、蜡熟期和完熟期9个时期,其中分蘖期是水稻生长过程中氮元素代谢最旺盛的阶段,合理施用分蘖肥可有效促进水稻秧苗快速长根、出叶、分蘖,增产丰收[1-2]。
目前,水稻分蘖肥施用的途径主要分为两种:一是以欧美为代表的水稻直播机械化栽培体系,水稻采用直播方式进行种植,在水稻分蘖期,普遍采用撒肥机完成分蘖肥撒施;二是以日本为代表的水稻移栽机械化栽培体系,水稻采用移栽方式进行种植,普遍采用机械插秧与侧深施肥同步作业,一次性将基肥和返青肥施在距离水稻秧苗根系一侧3~5 cm和深度5~8 cm处的侧深位置,但随着水稻秧苗根系的伸展,以施用颗粒状硫酸铵为代表的返青肥在促进水稻返青和水稻分蘖方面只能维持10 d左右肥效,为保证水稻分蘖期氮元素持续供应,一般在水稻插秧后10 d左右,通过人工或撒肥机对水稻行间追施以氮肥为主的分蘖肥[1-4]。以上两种栽培体系分别通过不同途径完成分蘖肥的施用,一定程度上可促进水稻秧苗分蘖,但两种途径的施肥方式存在施肥量不稳定、营养分布不均匀、污染水资源等问题,导致肥效利用率降低,水稻有效分蘖量较少,直接影响水稻产量。水稻深施肥技术是将肥料施入地基以下一定深度的位置,可减少氮肥使用量,有效提高肥效利用率,降低对水资源的污染[5-8]。
本文将已研制的深施肥装置安装于具有除草功能的行走装置[9-13]上,进行水田电动双行深施肥除草机设计。该机具采用电力驱动,通过控制机具前进速度和叶片开口直径以满足不同施肥量需求,可同步完成水稻分蘖肥深施和行间除草,从而减少作业次数,降低秧苗损伤,提高肥效利用率,减少环境污染。
1 农艺要求
黑龙江省种植水稻为一季稻,不同地区积温不同,插秧后返青期长短也不相同,最佳水稻行间除草时间为插秧后10~20 d,分蘖肥施用时间一般为人工撒施返青肥或插秧机侧深施肥后7~14 d,施肥量为45~90 kg/hm2,施肥深度不超过0.10 m,水稻分蘖肥深施和行间除草同步作业最佳时间为插秧后10~14 d。作业时,泥土深度0.18~0.20 m,水稻返青后控水,泥浆层深度0.02~0.05 m,秧苗的株距与行距分别为0.12、0.30 m,除草率在75%以上[14-16]。
2 整机结构与工作原理
水田电动双行深施肥除草机是一种适用于水稻插秧后10~14 d,将分蘖肥准确、定量地施在水稻两行中央地基以下0.05~0.10 m处的同时,完成行间除草作业的机具,具有结构紧凑、操作灵活、噪声小等特点。
机具整机结构如图1a所示,主要包括支撑架、电池、电动机、限深板、侧传动箱、深施肥装置、变向减速器、主动除草轮、被动除草轮、电压调节转把、电流调节控制器。其中侧传动箱由链轮、链条和链轮箱组成;深施肥装置由肥箱、螺旋钢丝、施肥量调节机构、防堵排肥机构和施肥靴组成。主动除草轮与被动除草轮通过转轴与支撑架铰接,陷深板通过螺栓固接于支撑架,电动机与变向减速器组合在一起与支撑架固接,电池放置在变向减速器上端,变向减速器左右两侧分别安装有侧传动箱和深施肥装置,侧传动箱下端与主动除草轮通过转轴连接,深施肥装置安装在被动除草轮与主动除草轮之间,固接于链轮箱外壁,肥箱内的螺旋钢丝与变向减速器输出轴连接,施肥量调节机构通过螺栓固接于肥箱下端排肥口,防堵排肥机构通过螺栓与施肥量调节机构下端固接,施肥靴插配在防堵排肥机构下端管口。电压调节转把、电流调节控制器等控制部件依次安装于支撑架上。
施肥量调节机构结构如图1b所示,主要包括上壳体、下壳体、环形叶片、步进电动机、主动齿轮、齿轮转动环。环形叶片、主动齿轮、齿轮转动环自上而下依次安装在上壳体和下壳体构成的腔体内,通过控制步进电动机达到调节施肥量的目的[12]。
机具作业时,电动机产生的驱动力矩经变向减速器和侧传动箱分别传递到主动除草轮和螺旋钢丝。主动除草轮的转动可驱使机具前进行驶并完成除草作业,通过转动电压调节转把,由电流调节控制器控制电动机的转速,实现对机具前进速度的无级调控;同时,螺旋钢丝的转动促使肥料由肥箱排出,控制深施肥装置施肥量调节系统,设定适宜叶片开口直径,肥料经施肥量调节机构和防堵排肥机构落入施肥靴已划出的沟槽内,然后由施肥靴尾端覆泥板以及被动除草轮完成覆土盖肥,最终实现水稻分蘖肥深施与行间除草的同步作业。机具作业原理如图2所示。
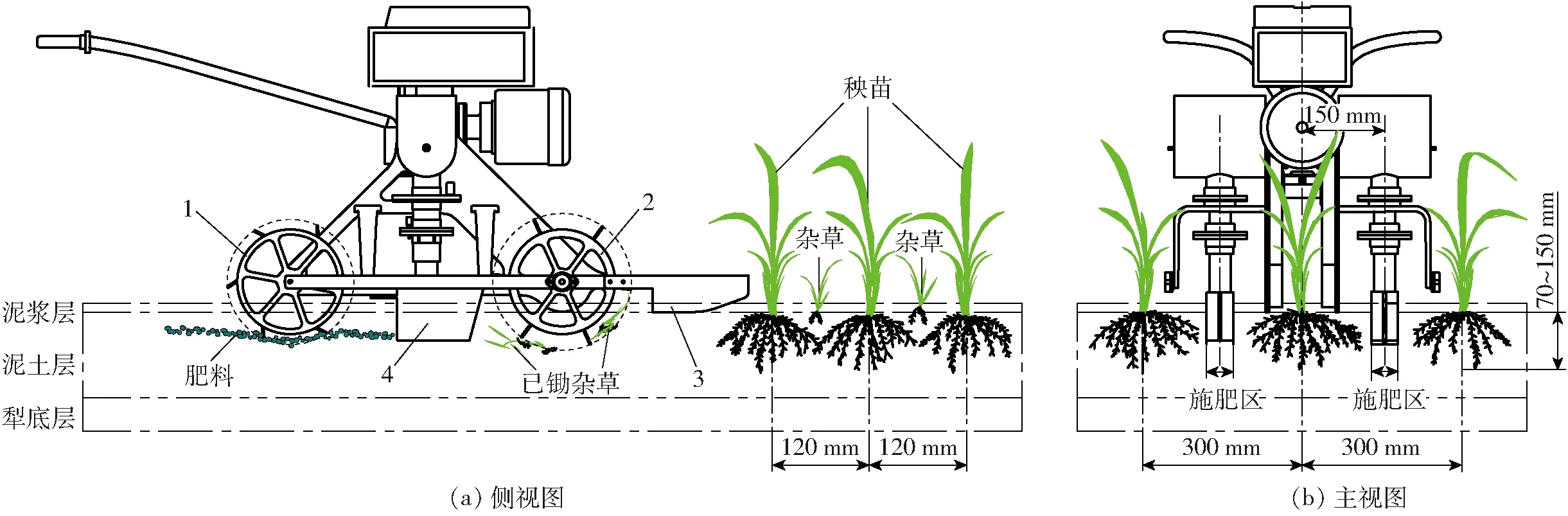
图2 水田电动双行深施肥除草机作业示意图Fig.2 Schematic diagram of electric control double row deep fertilizing weeder in paddy fields1.被动除草轮 2.主动除草轮 3.限深板 4.施肥靴
3 机具受力分析与系统设计
水田作业环境较为复杂,为保证水田电动双行深施肥除草机正常作业,本文根据达朗贝尔原理,通过对该机具被动除草轮、主动除草轮和机身(除了主动除草轮和被动除草轮以外其他部件的总成)进行动力学分析,计算主动除草轮所需最大驱动力矩,完成配套选型。
3.1 机具受力分析
水田电动双行深施肥除草机的触土部件为被动除草轮、主动除草轮以及机身的施肥靴和陷深板。机具的作业过程主要分为启动加速、平稳作业和制动减速3个阶段,其中启动加速阶段主动除草轮所需驱动力矩最大[17-19]。在启动加速过程中,由机具各部件运动状态可知,机身整体为平移加速运动,主动除草轮和被动除草轮为既做平移加速运动又做定轴加速转动的复合运动,机具受有惯性力和惯性力矩作用。因此,本文根据达朗贝尔原理对机具的启动加速阶段进行动力学分析,建立主动除草轮所需驱动力矩数学模型。
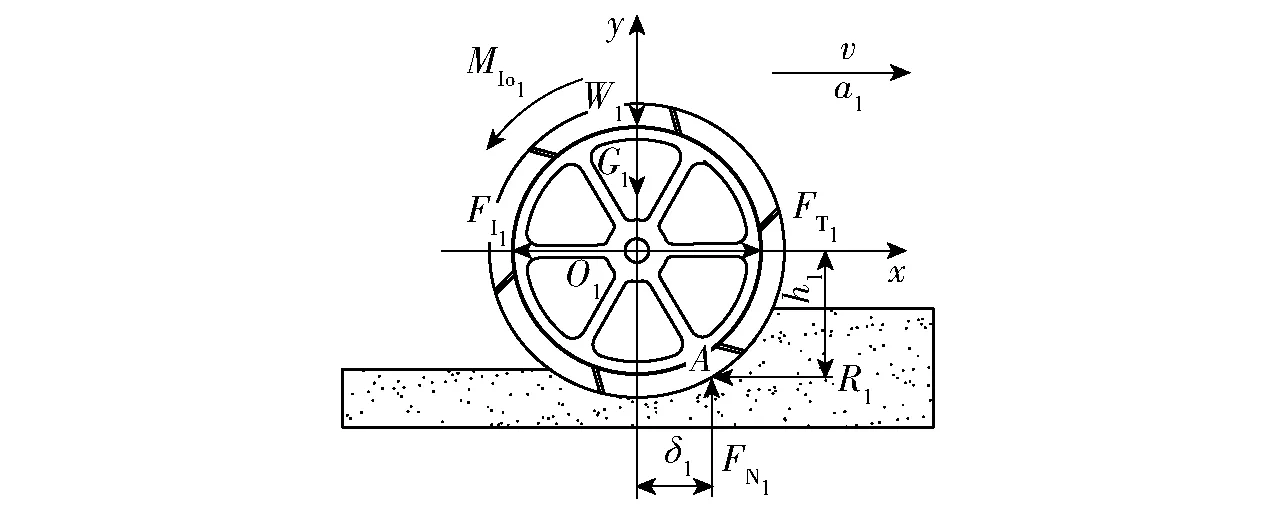
图3 被动除草轮受力分析Fig.3 Force analysis of passive weeding wheel
被动除草轮作为机具的从动轮,在土壤对被动除草轮的反作用力下前进运转,具有覆土盖肥、辅助除草、限制主动除草轮工作位置等功能,与文献[13]所述被动除草轮设计参数一致。机具启动加速过程中,被动除草轮受力情况如图3所示,主要有与机具前进方向相反的惯性力FI1;被动除草轮加速转动产生的惯性力矩MIo1;被动除草轮自身重力G1;机身对铰链点O1的垂直载荷W1;机身对被动除草轮的牵引力FT1,方向与机具前进方向相同;土壤与被动除草轮接触处作用有土壤对被动除草轮的法向反作用力Fn和切向摩擦力Fτ,假设Fn和Fτ的合力作用点为A,设合力的水平分量为R1,方向与机具前进方向相反,垂直分量为FN1,方向竖直向上。建立被动除草轮动力学平衡方程为
∑Fx=FT1-R1-FI1=0
(1)
∑Fy=FN1-G1-W1=0
(2)
∑MO1=R1h1-FN1δ1-MIo1=0
(3)
其中
R1=f1FN1FI1=m1a1MIo1=Jo1α1
式中f1——被动除草轮的滚动摩擦因数
m1——两个被动除草轮的质量,kg
a1——两个被动除草轮的加速度,m/s2
Jo1——两个被动除草轮关于旋转轴的转动惯量,kg·m2
α1——两个被动除草轮的角加速度(假设两个被动除草轮角加速度相同),rad/s2
δ1——合力作用点A与y轴的距离,m
h1——合力作用点A与x轴的距离,m
主动除草轮作为机具的驱动轮,电动机产生的驱动力矩经过变向减速箱减速增扭后传递到主动除草轮,在土壤对主动除草轮的反作用力下前进运转,进而带动机身和被动除草轮行进,完成深施肥与行间除草作业。受限于水田土壤较柔软、硬度较低、受力易变性等特性,主动除草轮在前进运转过程中使土壤发生沿切向方向的移动,主动除草轮不可避免存在滑转现象,即机具实际行走距离相比理论行走距离减小,滑转现象严重会导致主动除草轮驱动能力降低,机具功率消耗增大,甚至无法前进,直接影响机具作业质量。为减少主动除草轮滑转,根据轮子滚动前进条件,对主动除草轮结构进行改进,以增大极限土壤推进力[20-23]。如图4所示,改进后的主动除草轮主要包括轮盘、板齿和轴套,其滚动半径、宽度以及耙齿长度和数量与文献[13]所述主动除草轮设计参数保持一致,将耙齿更换为板齿,并沿轮盘法向方向均布焊接于2个轮盘之间,通过增加土壤与板齿法向接触面积来增加对土壤的切向压力,进而增加极限土壤推进力;将轮盘由全盘式改为镂空式,以防止主动除草轮被泥土堵塞,影响机具作业质量。
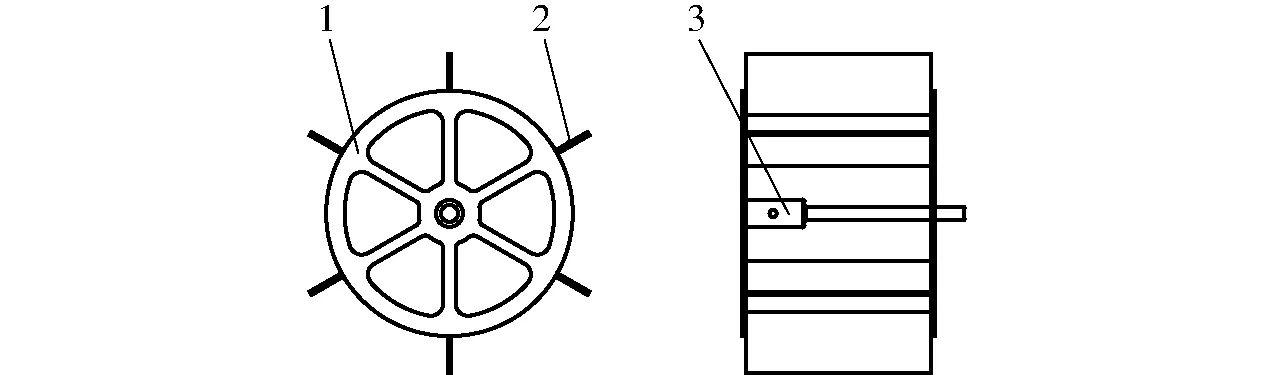
图4 改进后主动除草轮结构图Fig.4 Structure diagram of improved active weeding wheel1.轮盘 2.板齿 3.轴套
机具启动加速过程中,主动除草轮受力情况如图5所示,主要有与机具前进方向相反的惯性力FI2;主动除草轮加速旋转产生的惯性力矩MIo2;电动机传递到主动除草轮的驱动力矩Md;主动除草轮自身重力G2;机身对铰链点O2的垂直载荷W2;机身对主动除草轮的牵引阻力FT2,方向与机具前进方向相反;土壤与主动除草轮接触处作用有土壤对主动除草轮的滚动阻力R和由驱动力矩产生的驱动力对土壤作用时所产生的反作用力PT,假设R和PT的合力作用点为B,设合力的水平分量为R2,方向与机具前进方向相同,垂直分量为FN2,方向竖直向上。建立主动除草轮动力学平衡方程为
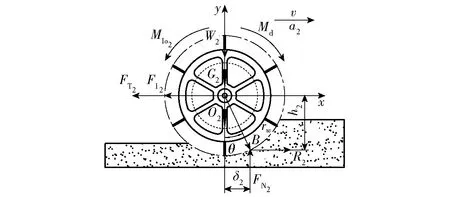
图5 主动除草轮受力分析Fig.5 Force analysis of driving weeding wheel
∑Fx=R2-FT2-FI2=0
(4)
∑Fy=FN2-G2-W2=0
(5)
∑MO2=Md-FN2δ2-R2h2-MIo2=0
(6)
其中
R2=f2FN2FI2=m2a2MIo2=Jo2α2
式中f2——主动除草轮的滚动摩擦因数
m2——两个主动除草轮的质量,kg
a2——两个主动除草轮的加速度,m/s2
Jo2——两个主动除草轮关于旋转轴的转动惯量,kg·m2
α2——两个主动除草轮的角加速度,rad/s2
δ2——合力作用点B与y轴的距离,m
h2——合力作用点B与x轴的距离,m
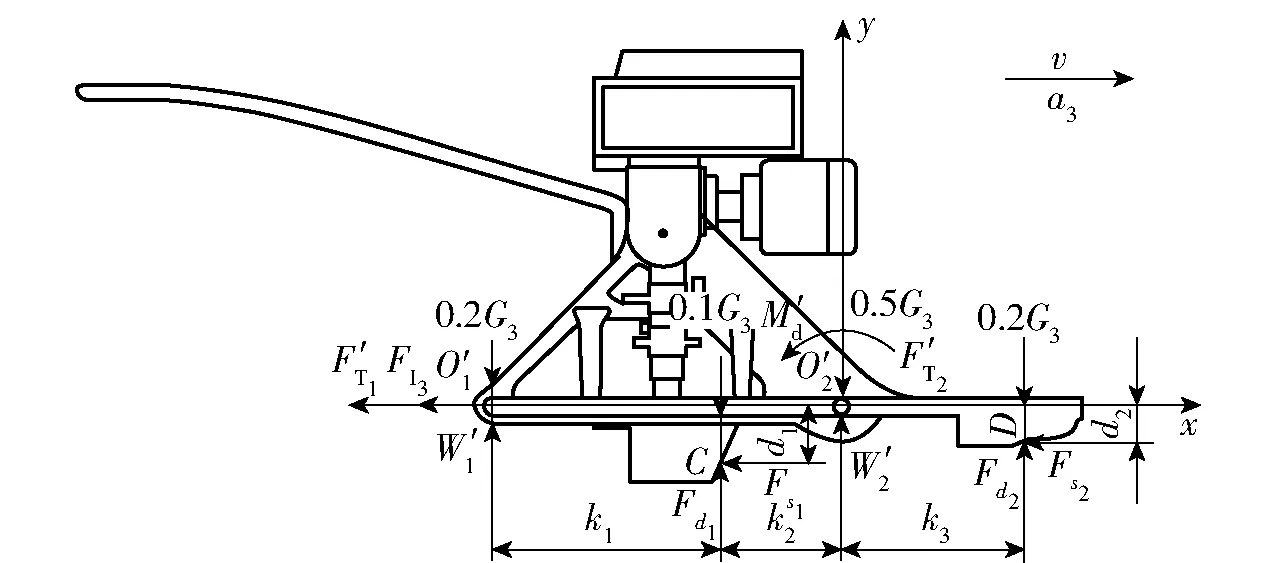
图6 机身受力分析Fig.6 Force analysis of fuselage
机身在被动除草轮与主动除草轮驱动下前进,其触土部件为陷深板和深施肥装置的施肥靴。机具加速启动过程中,机身受力情况如图6所示,主要有与机具前进方向相反的惯性力FI3;机身自身重力G3;驱动力矩对铰链点O′2的反作用力矩M′d;铰链点O′1对机身的支撑反力W′1;铰链点O′2对机身的支撑反力W′2;被动除草轮对机身的拉力F′T1;主动除草轮对机身的牵引力F′T2;土壤对施肥靴的滑动摩擦力Fs1;土壤对陷深板的滑动摩擦力Fs2;土壤对施肥靴的垂直反力Fd1;泥土对陷深板的垂直反力Fd2。建立机身动力学平衡方程为
∑Fx=F′T2-F′T1-Fs1-Fs2-FI3=0
(7)
∑Fy=Fd1+Fd2+W′1+W′2-G3=0
(8)
∑MO′2=(W′1-0.2G3)(k1+k2)+(Fd1-0.1G3)k2+Fs1d1+Fs2d2-M′d-(Fd2-0.2G3)k3=0
(9)
其中
Fs1=μ1Fd1Fs2=μ2Fd2FI3=m3a3
式中μ1——施肥靴的滑动摩擦因数
μ2——陷深板的滑动摩擦因数
m3——机身总质量,kg
a3——机身加速度,m/s2
d1——作用点C与x轴的距离,m
d2——作用点D与x轴的距离,m
k1——铰链点O′1与作用点C的距离,m
k2——作用点C与y轴的距离,m
k3——作用点D与y轴的距离,m
根据受力关系可知,W1=W′1,W2=W′2,FT1=F′T1,FT2=F′T2,联立式(1)、(2)、(4)、(5)、(7)、(8)可得
(1-f1)FN1+(1+f2)FN2+(1-μ1)Fd1+(1-μ2)Fd2-(G1+G2+G3)-(m1a1+m2a2+m3a3)=0
(10)
其中
G1+G2+G3=G0=m0g
a1=a2=a3=am1+m2+m3=m0m1a1+m2a2+m3a3=m0a
式中m0——机具整机总质量,kg
a——机具整机加速度,m/s2
联立式(6)、(10)可得

(11)
为使驱动力矩满足机具启动加速需求,令μ1=μ2=f1=f2=1,则Fs1=Fd1,Fs2=Fd2,R1=FN1,R2=FN2,由式(11)可知
(12)
如图5所示,根据几何关系建立rw、δ2、h2三者的函数关系
(13)
式中rw——主动除草轮无滑转时滚动半径,m
θ——作用点B所处半径与y轴负半轴的夹角,(°)
在机具启动加速过程中,主动除草轮不可避免存在滑转现象,滑转程度用滑转率表示为
(14)
式中η——主动除草轮的滑转率,%
r——主动除草轮滑转时的滚动半径,m
则主动除草轮角加速度与机具整机加速度的关系为
(15)
联立式(12)、(13)、(15),可得
(16)
令b=sin(π/4+θ),由三角函数性质可知,当θ=2kπ+π/4且k=0时,b取得最大值1,则Md取相应最大值为
(17)
农业机械在田间作业时行走轮的滑转率一般为3%~8%,水田作业环境较为复杂,滑转率较高,取最大允许滑转率20%[24-26];水田电动双行深施肥除草机为单人作业机具,可单手拉起,要求机具结构紧凑,尽量轻简化,设计整机载肥状态下总质量为35 kg;主动除草轮无滑转时的滚动半径参考文献[13],取值为0.15 m;由于主动除草轮结构较为复杂,其惯性张量很难精确算出,本文通过Pro/E软件对主动除草轮的三维模型进行质量属性分析,材质选择密度为2.79×103kg/m3的铝合金,得到两个主动除草轮关于旋转轴的转动惯量7.15×10-3kg·m2;根据农艺要求,机具正常的作业速度为0.4~0.6 m/s,为保证机具作业质量,机具启动加速阶段所用时间越短越好,时间应控制在0.1 s以内,假设机具在启动加速过程中做匀加速运动,在电动机达到额定功率之前机具前进速度能够满足正常作业速度需求,加速度取值为6 m/s2。由式(17)计算得到主动除草轮所需最大驱动力矩理论值为59.05 N·m。
3.2 控制系统设计
水田电动双行深施肥除草机控制系统主要包括深施肥装置控制系统和机具行走控制系统。
3.2.1深施肥装置控制系统
深施肥装置控制系统硬件结构如图7a所示,主要包括电池、步进电动机、直流电动机、红外遥控器、红外接收管、L298N电动机驱动模块(步进电动机驱动模块和直流电动机驱动模块)、STC89C52RC单片机、肥量调节机构和防堵排肥机构。其系统硬件原理框图如图7b所示。
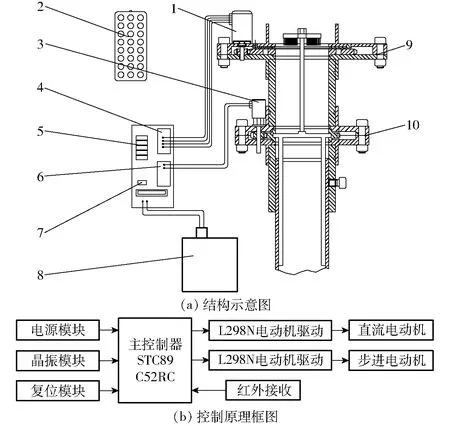
图7 深施肥装置控制系统硬件结构图Fig.7 Structure design of control system hardware of deep fertilizer device1.步进电动机 2.红外遥控器 3.直流电动机 4.步进电动机驱动模块 5.STC89C52RC单片机 6.直流电动机驱动模块 7.红外接收管 8.电池 9.肥量调节机构 10.防堵排肥机构
如图8所示,深施肥装置控制系统软件主要包括控制电动机转动的STC89C52RC单片机主程序和红外解码子程序。其中,“motor=0”、“zheng_flag=1”、“fan_flag=1”、“zheng_run=1”和“fan_run=1”分别为直流电动机转动控制、步进电动机正转一个角度、步进电动机反转一个角度、步进电动机连续正转和步进电动机连续反转的标志变量,编码值为8个16进制数据,解析为相应内容。该控制系统由电池供电,以STC89C52RC单片机为主控,设定肥量调节机构叶片开口直径时,按动红外遥控器相应定义控制按键,红外遥控器将电信号转化为红外信号经红外接收管传输给STC89C52RC单片机,STC89C52RC单片机将红外信号转换为电信号传递给步进电动机驱动模块,控制步进电动机转动一定步数,完成开口直径大小的调节;防堵排肥机构的控制方式与肥量调节机构类似,不同点是驱动电动机为直流电动机,通过红外遥控器控制直流电动机的运行与停止来调整防堵排肥机构的工作状态。
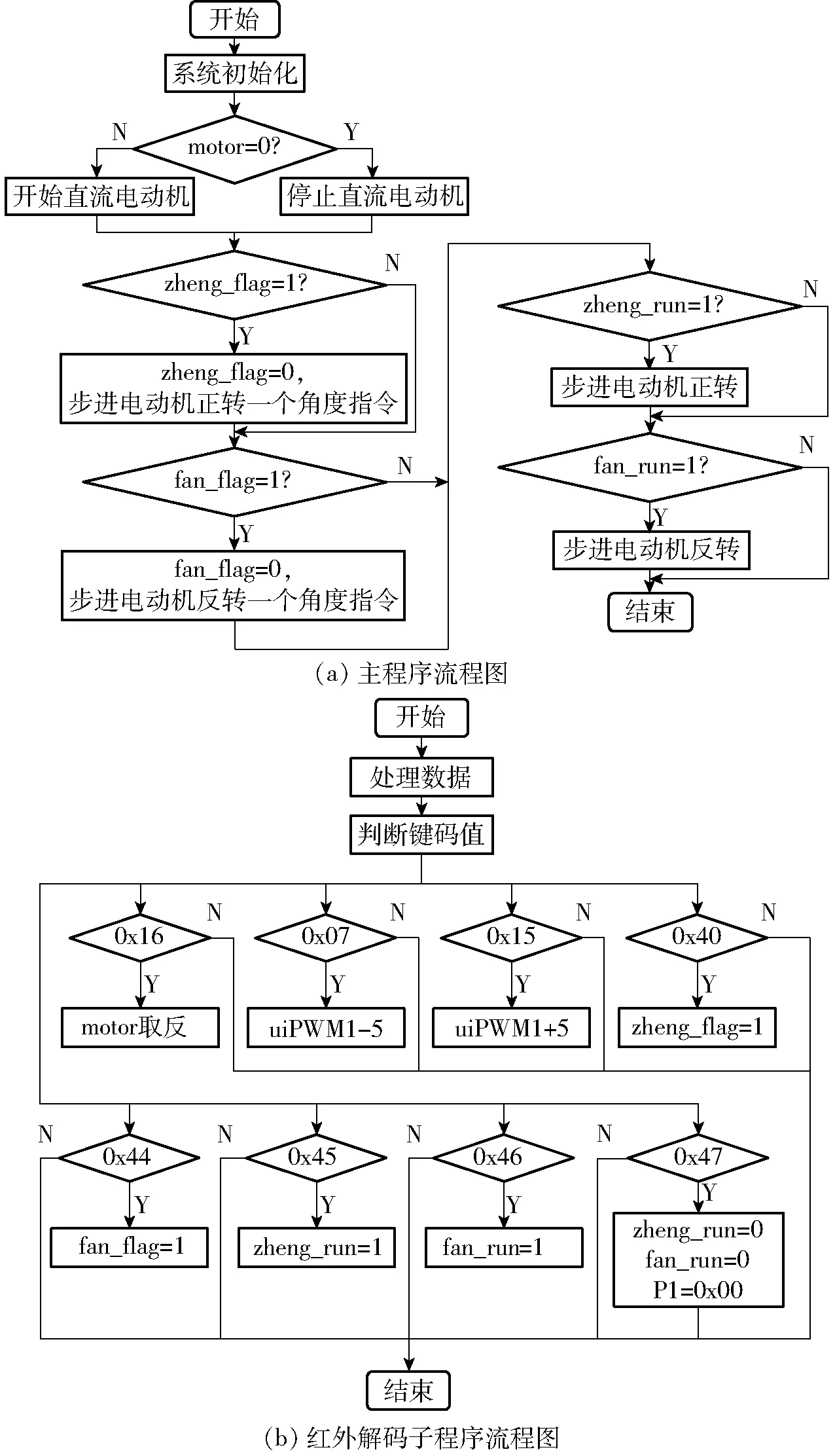
图8 深施肥装置控制系统软件流程图Fig.8 Flow chart of deep fertilizer device control system software
3.2.2机具行走控制系统
如图9所示,机具行走控制系统主要包括电池、电动机、电压调节转把和电流调节控制器。电流调节控制器分别与电池、电动机和电压调节转把连接。

图9 机具行走控制系统实物图Fig.9 Electronic controlled deep fertilizing device for paddy filed1.电压调节转把 2.电池 3.电流调节控制器 4.电动机
电压调节转把选取可匹配12~99 V电动机的通用型霍尔元件转把;电流调节控制器选用60 V/500 W控制器;电动机选用无刷差速电动机,额定功率为500 W,额定转速为3 000 r/min,额定力矩为1.59 N·m。
通过对主动除草轮进行运动学分析可知[9,23],其瞬时转速为
(18)
式中ω——主动除草轮的角速度,rad/s
v——机具的前进速度,m/s
由式(18)可知,当主动除草轮滑转率达到最大允许值20%,机具前进速度最大为0.6 m/s时,主动除草轮的瞬时转速达到最大转速为48 r/min。根据电动机额定转速,变向减速器传动比应大于1/62;电动机产生的力矩经变向减速器减速增扭后传递到主动除草轮,主动除草轮所需最大驱动力矩理论值为59.05 N·m,根据电动机额定力矩,变向减速器传动比应小于1/37。结合机具结构,主变速箱选取减速器传动比为1/50的RV系列蜗轮减速器,则主动除草轮的瞬时转速最大为60 r/min,电动机产生的力矩经变向减速器减速增扭后传递到主动除草轮的驱动力矩为79.50 N·m。由此可知,所选的电动机与变向减速器组合满足机具启动加速时主动除草轮所需最大瞬时转速和驱动力矩的要求。
电池的选型既要满足电动机的额定功率,同时要求具有一定的续航能力,电池选用电压容量为60 V/20 A·h的锂电池。锂电池的工作时长为
(19)
式中C——电池容量,A·h
P——电动机额定功率,W
U——电动机额定电压,V
由式(19)计算可得,电动机在额定功率下工作时,锂电池理论工作时长为2.4 h,满足机具实际作业时长需求。
4 台架试验
参考NY/T 1003—2006《施肥机械质量评价技术规范》,运用试验设计与分析的方法对深施肥装置的施肥稳定性和施肥均匀性进行研究。通过预试验确定前进速度和叶片开口直径为影响深施肥装置施肥性能的主要因素,并得到合理的取值范围,然后进行二次正交旋转组合试验,分析得到影响因素分别与施肥均匀性施肥量均值和施肥均匀性变异系数之间的关系。
4.1 试验材料与方法
试验在东北农业大学排种性能实验室进行,试验材料为粒径2~5 mm,容重1.35×103kg/m3,含水率19.4%,自然休止角35.8°,含氮量在46.4%以上的颗粒状尿素。
依据NY/T 1003—2006《施肥机械质量评价技术规范》,施肥稳定性测定为静态试验,不考虑前进速度,分析深施肥装置不同叶片开口直径下相同时间内排肥量的变化规律;施肥均匀性测定为动态试验,沿机具前进方向按0.1 m长度连续等分不少于30段的距离,分别收集落在各小段内的尿素颗粒并称量其质量。施肥稳定性和施肥均匀性由施肥量均值、施肥量标准差和变异系数衡量。
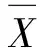
(20)
式中Xi——测定施肥稳定性时表示每相同时间内排出尿素颗粒的质量;测定施肥均匀性时表示每小段内落入尿素颗粒的质量,g
m——测定次数
施肥量标准差σ为
(21)
变异系数V为
(22)
试验台架主要由安装架、深施肥装置、肥料收集带和JPS-12型排种性能检测试验台组成,如图10所示。试验时,深施肥装置固定于安装架,将自制每小段长度为0.1 m,总长度为4 m的肥料收集带放置于JPS-12型排种性能检测试验台的传送带,用于施肥均匀性测定时收集深施肥装置下落的尿素颗粒,然后利用调速器控制深施肥装置螺旋钢丝转动及叶片开口直径的大小,通过调节JPS-12型排种试验台电动机变频器频率控制传送带(肥料收集带)相对于深施肥装置反向运动,模拟深施肥装置前进速度。

图10 深施肥装置试验台架Fig.10 Test bench of deep fertilizing device1.深施肥装置 2.安装架 3.JPS-12型排种性能检测试验台 4.肥料收集带
4.2 试验结果与分析
4.2.1施肥稳定性
施肥稳定性测定初始,肥箱为满肥状态,且肥量低于肥料箱容积1/4时停止试验。用电子天平称量叶片开口直径分别为14、15、16、17、18、19、20 mm时深施肥装置10 s内排出尿素颗粒的质量,重复5次,由式(20)~(22)计算施肥稳定性施肥量均值y1和施肥稳定性变异系数y2。试验结果如表1所示。
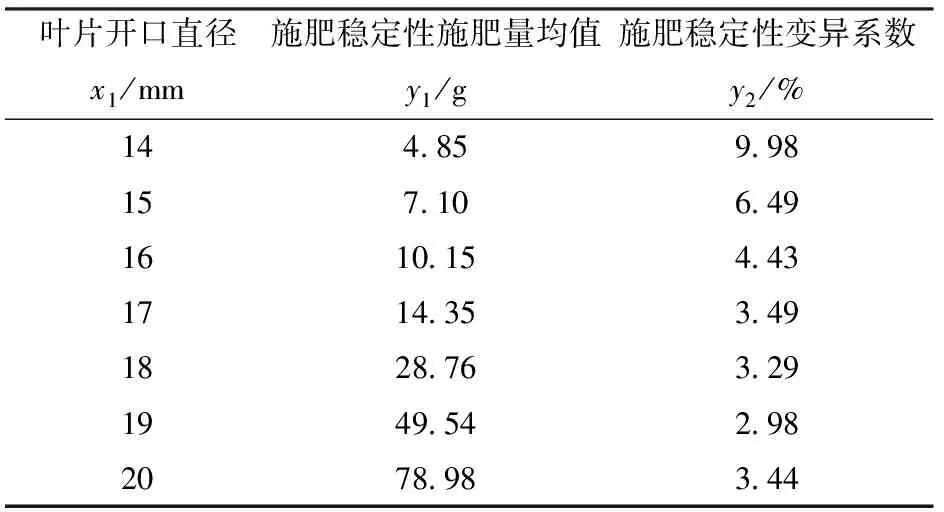
表1 不同开口直径下的施肥稳定性性能Tab.1 Fertilization stability under different opening diameters of fertilizer regulation mechanism
应用Design-Expert软件对表1结果进行方差分析,叶片开口直径对施肥稳定性施肥量均值和施肥稳定性变异系数的模型影响显著,叶片开口直径影响施肥稳定性施肥量均值和施肥稳定性变异系数的回归方程分别为
(23)
(24)
由式(23)、(24)可知,当叶片开口直径在一定范围内时,随着叶片开口直径的增大,施肥稳定性施肥量均值逐渐增大,施肥稳定性变异系数逐渐减小。为判断深施肥装置是否满足NY/T 1003—2006《施肥机械质量评价技术规范》中施肥稳定性变异系数小于7.8%的要求,设机具前进速度为0.5 m/s,求得最小施肥量45 kg/hm2时叶片开口直径为15.74 mm,施肥稳定性变异系数为6.08%,说明该施肥装置的施肥稳定性较好。
4.2.2施肥均匀性
通过对深施肥装置施肥性能进行预试验,确定影响施肥均匀性施肥量均值和施肥均匀性变异系数的主要因素包括前进速度和叶片开口直径,得到各影响因素的取值范围:叶片开口直径为15~19 mm,前进速度为0.4~0.6 m/s,在此基础上采用二次正交旋转组合进行试验分析,试验因素编码如表2所示。
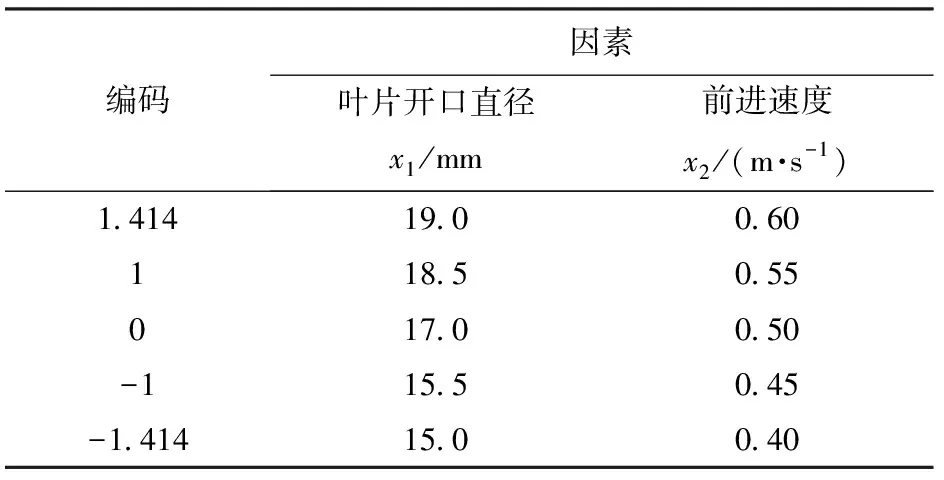
表2 试验因素编码Tab.2 Factors coding
根据二次正交旋转组合设计16组试验,分别收集落在各小段内的颗粒尿素并称量其质量,由式(20)~(22)计算施肥均匀性施肥量均值y3和施肥均匀性变异系数y4。试验方案与结果见表3。
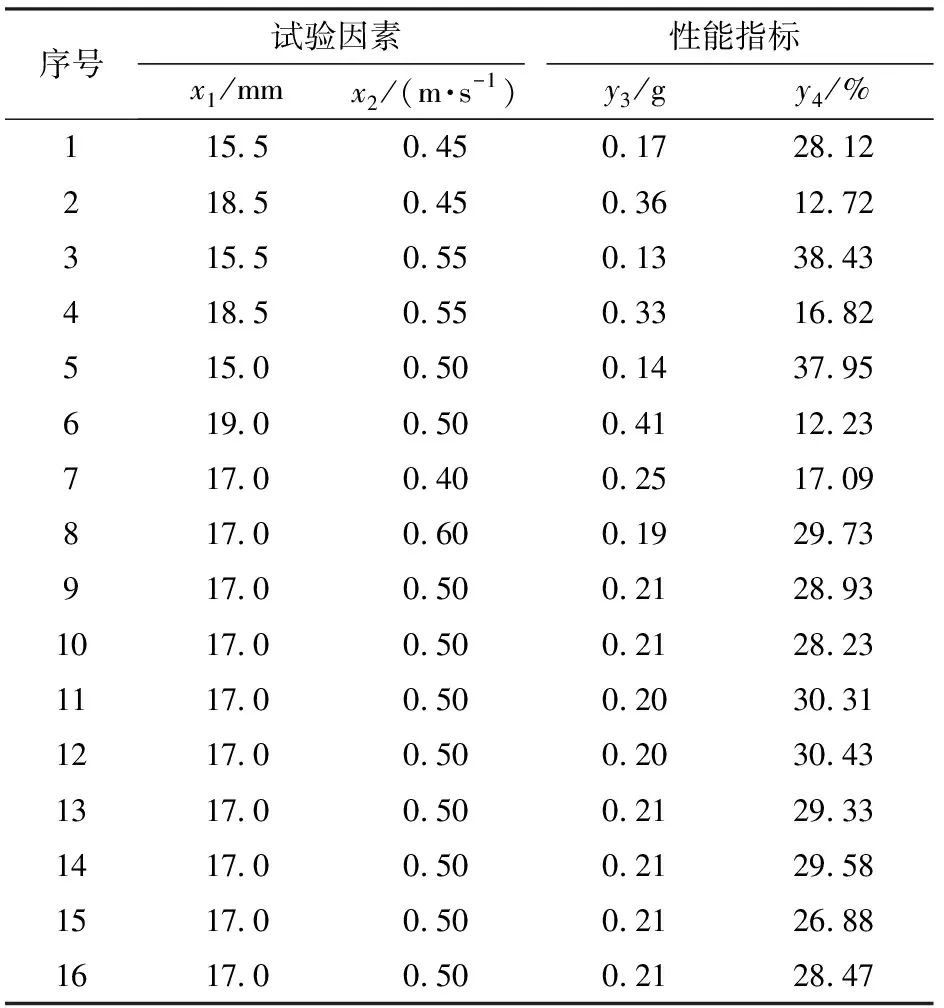
表3 试验方案与结果Tab.3 Trial protocols and results
4.2.2.1施肥均匀性施肥量均值
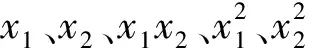
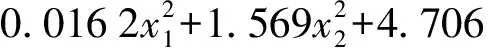
(25)
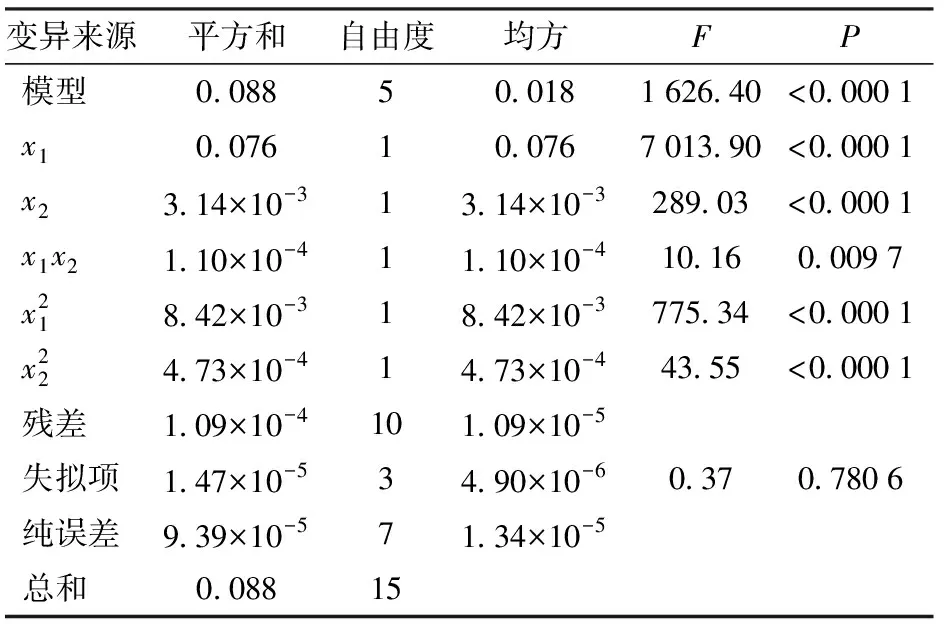
表4 施肥均匀性施肥量均值方差分析Tab.4 Variance analysis on mean value of fertilization of fertilization uniformity
根据回归方程(25),利用Design-Expert软件绘制出叶片开口直径和前进速度对施肥均匀性施肥量均值的响应曲面,如图11所示。
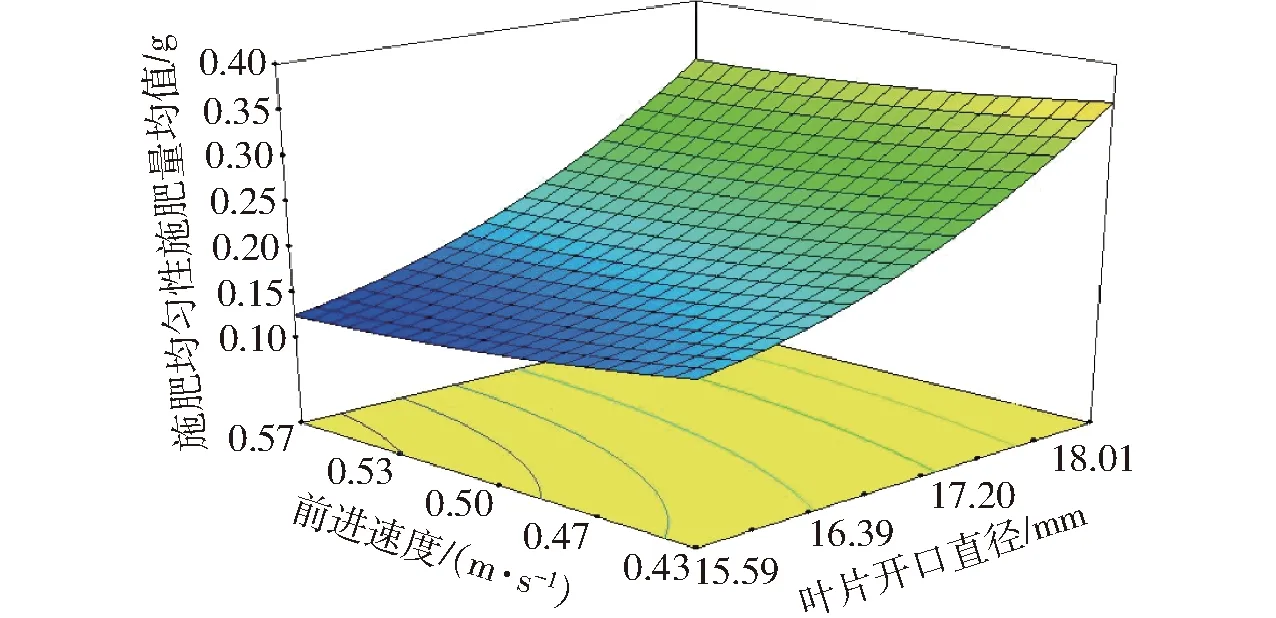
图11 各因素对施肥均匀性施肥量均值的响应曲面Fig.11 Response surface of all factors to mean value of fertilization of fertilization uniformity
由图11可知,当前进速度一定时,施肥均匀性施肥量均值随着叶片开口直径的增大而增大;当叶片开口直径一定时,施肥均匀性施肥量均值随着前进速度的增大而减小。深施肥装置通过调节叶片开口直径大小控制排肥量,叶片开口直径越大,排出的肥量越大,反之越小。当叶片开口直径处于低水平时,施肥装置单位时间内排出的肥量为定值且较少,随着前进速度的增大,下落到每段收集盒内的肥量相应减少,即施肥均匀性施肥量均值减小,此时影响施肥均匀性施肥量均值的主要因素为前进速度;当叶片开口直径处于高水平时,施肥装置单位时间内排出的肥量为定值且较多,随着前进速度的增大,下落到每段收集盒内的肥量相应减少,即施肥均匀性施肥量均值减小,此时影响施肥均匀性施肥量均值的主要因素为叶片开口直径。
4.2.2.2施肥均匀性变异系数
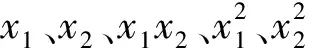
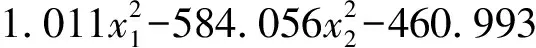
(26)

表5 施肥均匀性变异系数方差分析Tab.5 Variance analysis of fertilization uniformity variation coefficient
根据回归方程(26),利用Design-Expert软件绘制出叶片开口直径和前进速度对施肥均匀性变异系数的响应曲面,如图12所示。
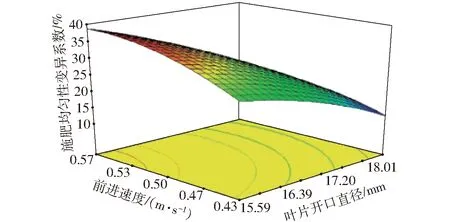
图12 各因素对施肥均匀性变异系数的响应曲面Fig.12 Response surface of all factors to the variation coefficient of fertillization uniformity
由图12可知,当前进速度一定时,施肥均匀性变异系数随着叶片开口直径的增大而减小;当叶片开口直径一定时,施肥均匀性变异系数随着前进速度的增大而增大。试验所用肥料为颗粒状尿素,试验时,肥料颗粒从叶片开口处排出,当叶片开口直径处于低水平时,排肥量较小,而且肥料为形状大小不一的固态颗粒,表面为凹凸非光滑曲面,易在下落口处挤压结拱,影响肥料颗粒下落,随着前进速度的增大,下落到每段收集盒内的肥量随之减少,甚至出现断条,施肥均匀性较低,此时影响施肥均匀性变异系数的主要因素为叶片开口直径;当叶片开口直径处于高水平时,排肥量较大,结拱现象减弱,肥料颗粒下落顺畅,连续性增强,施肥均匀性提高,但随着前进速度的增大,施肥均匀性同样会随之降低,此时影响施肥均匀性变异系数的主要因素为前进速度。
4.3 参数优化
根据农艺要求,深施肥装置施肥量调节范围为45~90 kg/hm2,施肥均匀性变异系数控制在NY/T 1003—2006《施肥机械质量评价技术规范》中规定的40%以内,且越小越好。因此,对该施肥装置在常规施肥量67.5 kg/hm2情况下的各项作业参数进行优化求解,得到相应的施肥均匀性变异系数。其约束函数为
(27)
根据约束函数模型,利用Design-Expert软件对回归方程(25)、(26)进行优化求解,得到在施肥均匀性施肥量均值目标值为0.20 g情况下影响施肥均匀性变异系数的各参数组合,如图13所示阴影区域,选取其中施肥均匀性变异系数最低的参数组合作为最优,即叶片开口直径为16 mm,前进速度为0.40 m/s,此时施肥均匀性施肥量均值为0.20 g,施肥均匀性变异系数为21.7%。
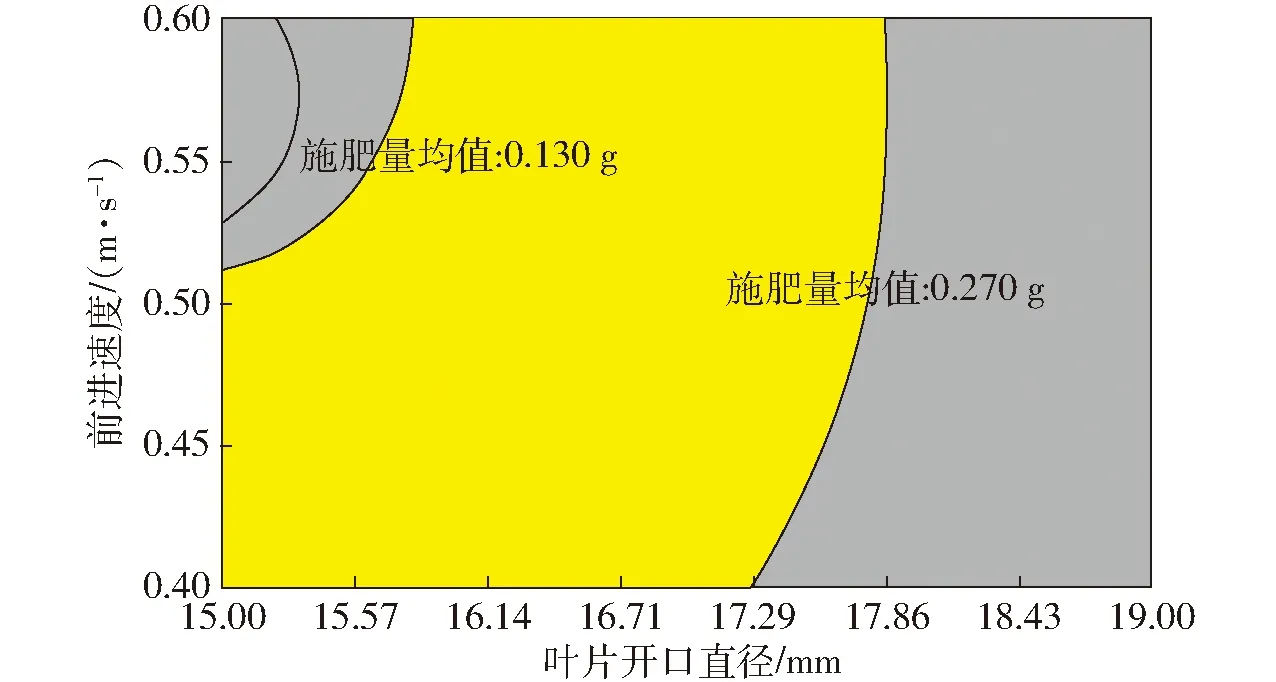
图13 优化区域Fig.13 Optimized area
5 田间试验
5.1 试验条件
为检验机具的田间作业性能,于2017年6月15日在黑龙江省哈尔滨市阿城区新乡试验田内进行施肥量偏差和除草率测定,水稻种植采用机械插秧和侧深施肥同步作业,未经化学或人工除草。试验于插秧后10 d进行,水稻品种为龙洋16,长势良好,株距0.12 m,行距0.30 m,苗高约0.26 m,泥浆层深度约0.05 m,泥土深度约0.17 m,杂草数量约20株/m2,杂草主要以水田稗(平均株高约0.12 m,根系平均深度约0.19 m)为主,有少量野慈姑。田间试验如图14所示。

图14 水田电动双行深施肥除草机田间试验Fig.14 Field experiment of electric control double row deep fertilizing weeder in paddy fields
5.2 施肥量偏差试验
施肥量偏差测定试验时,给定施肥量为67.5 kg/hm2,选取5块2.4 m×30 m的矩形区域作为施肥量偏差测定的试验田块,试验前对肥箱内肥料进行称量,叶片开口直径设为16 mm,机具以0.40 m/s的速度进行作业,试验结束后称量肥箱内剩余肥料质量,计算施肥量偏差
(28)
式中γs——施肥量偏差,%
Wq——试验前肥箱内肥料质量,kg
Wh——试验后肥箱内剩余肥料质量,kg
S——施肥作业面积,m2
F——给定施肥量,kg/hm2
试验结果如表6所示,当给定施肥量为67.5 kg/hm2,叶片开口直径16 mm,机具前进速度0.4 m/s时,施肥量偏差控制在3.54%以内,深施肥装置施肥量总体比较稳定。
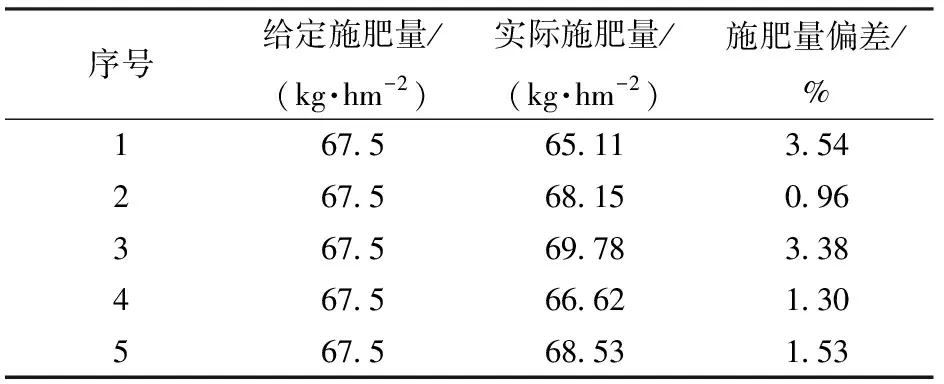
表6 施肥量偏差测定统计表Tab.6 Statistical result for measuring fertilization deviation
5.3 除草率试验
机具前进速度是影响水田机械除草效果的重要因素,以机具前进速度为试验因素,除草率为评价指标进行单因素试验,另外选取5块2.4 m×30 m的矩形区域作为不同前进速度下除草率测定的试验田块,然后在不同前进速度的试验田块内任意选取5个1 m×1 m区域为测试区,计算除草率后取平均值。
(29)
式中Y——除草率,%
Q1——除草前测试区杂草总数,株
Q2——除草后测试区杂草总数,株
试验结果如表7所示,水田电动双行深施肥除草机除草率均不小于78.5%,除草效果较优,满足农艺要求。

表7 不同前进速度下机具除草率Tab.7 Weeding rate of implements at different forward speeds
6 结论
(1)根据达朗贝尔原理,对被动除草轮、主动除草轮和机身进行动力学分析,建立主动除草轮所需驱动力矩数学模型,得到主动除草轮所需最大驱动力矩理论值为59.05 N·m,完成深施肥装置控制系统与机具行走控制系统设计。
(2)对深施肥装置进行台架试验,试验采用二次正交旋转组合设计,得到机具前进速度与叶片开口直径分别对施肥均匀性施肥量均值和施肥均匀性变异系数的影响规律,优化结果表明:在机具前进速度为0.40 m/s,叶片开口直径为16 mm的条件下,施肥均匀性施肥量均值为0.20 g,施肥均匀性变异系数最小值为21.7%。
(3)对机具进行田间性能试验,当给定施肥量为67.5 kg/hm2,叶片开口直径16 mm,机具前进速度0.40 m/s时,施肥量偏差控制在3.54%以内;不同前进速度下除草率均不小于78.5%,机具满足水稻分蘖肥深施和行间除草的农艺要求。
