平地向坡地转换喷灌水量分布计算模型研究

张 林 惠 鑫 陈俊英

(1.西北农林科技大学水土保持研究所，陕西杨凌 712100； 2.西北农林科技大学水利与建筑工程学院，陕西杨凌 712100)

0 引言

喷灌均匀度是喷灌系统设计的一个重要参数，单喷头水量分布是喷灌均匀度计算的最基本资料之一[1-3]。关于喷灌水量分布和均匀度计算方面，以往的研究较多[4-13]。朱兴业等[4]采用Matlab语言编制程序，对不同喷头组合间距下的水量分布及均匀系数进行了模拟仿真计算，初步提出了旋转式射流喷头在正方形布置时的最佳组合间距。严海军等[5]对两种园林地埋式喷头组合喷洒性能进行了模拟试验，结果表明，在最大零漏喷范围内，喷灌均匀系数与组合形式关系不大，主要取决于喷头结构及其径向水量分布。TARJUELO等[6-7]分别研究了喷头在无风和有风条件下水量分布的影响因素，结果表明，风速对水量分布的影响显著。MANTOVANI等[8]和LI[9]分析了喷灌均匀性对作物产量的影响。ZHANG等[10]、MATEOS[11]均对大田尺度下喷灌均匀性进行了研究，初步建立了大田尺度下喷灌系统均匀度计算模型。这些研究对喷灌系统设计及技术推广应用起到了重要作用。但纵观这些研究，主要以平地喷灌为主。随着喷灌技术逐步向丘陵山区发展，坡地喷灌系统设计成为当前急需解决的重要技术问题。

坡地喷灌水量分布对于坡地喷灌系统设计至关重要，但受地形影响，实测坡地喷灌水量分布往往比较困难，而平地水量分布获取相对简单，因此有学者试图通过一些方法将喷灌水量分布由平地转换到坡地，从而便于坡地喷灌研究。陈学敏等[14]基于动力学原理推导出水滴运动方程，并结合水量平衡原理，构建出坡地喷灌水量分布计算模型，但模型假定水流在喷嘴出口处就完全碎裂，这与实际不太相符，影响了计算结果的准确性。向清江等[15]以射流轨迹计算公式[16]为基础，采用网格变换的方式实现了平地和坡地之间水量分布数据的转换，但该方法在假定射流的射程损失时过于简化，因此数据转换准确性还需进一步验证；张以升等[17]以弹道理论为基础，考虑水滴运动蒸发，建立了坡地喷灌水量分布计算模型，但该模型做了较多假设，使得模型只能在较为理想的状态下使用，不具有普适性。

针对上述问题，本文以坡地喷头射程计算公式[18]为基础，根据喷头射流方向总水量守恒原理，构建喷灌水量分布由平地转换到坡地的计算模型，并通过试验验证模型的正确性。最后利用该模型，分析喷头工作压力、布置方式和间距等对坡地喷灌水量分布的影响，以期为坡地喷灌系统设计提供一定的科学依据。

1 现有基础

引用文献[18]推导出的坡地喷头射程计算公式

Rup=R0cosβ(1-tanβcot(θ+β))

(1)

Rdown=R0cosβ(1+tanβcot(θ-β))

(2)

式中Rup——喷头在上坡方向的射程，m

Rdown——喷头在下坡方向的射程，m

R0——喷头在平地上的射程，m

β——投影角，即喷射水流运动轨迹线在坡面上的投影线和平地上的投影线之间的夹角，(°)

θ——喷射水流运动轨迹线与平地的夹角，即射流末端水滴落地角度，(°)

已知地形坡度，给定喷头在坡面上的旋转角，可计算出投影角

(3)

式中i——地形坡度

α——喷头旋转角，(°)

当0°≤α≤180°时，β取正号；当180°<α<360°时，β取负号。

2 单喷头水量分布由平地向坡地转换的计算模型

2.1 模型构建思路

在喷头工作参数(如压力等)不变的条件下，喷头出流量会保持不变，假定喷头旋转速度均匀，那么无论是平地或坡地，不同旋转角下沿喷头射流方向上总水量保持不变。已知地形坡度，根据上述坡地喷头射程计算公式，可以获得不同喷头旋转角下的坡面射程；结合平地上实测的喷头径向水量分布数据，基于沿喷头射流方向总水量守恒原理，利用喷头坡面射程与平地射程比例，将平地实测水量转换为坡地水量，进而获得整个坡面水量分布。

2.2 平地和坡地之间的坐标转换

2.2.1上坡方向坐标转换

如图1所示，曲线O′M′nMn为上坡方向喷头射流运动轨迹，射流在平地上的落点为Mn，在上坡面对应的落点为M′n，假定Mn在平地上的坐标为(xn，yn)(其横、纵坐标轴所在平面为平地地面)、M′n在上坡面上的坐标为(x′n,y′n)(其横、纵坐标轴所在平面为坡面)，通过对图1解立体几何可知Mn的横、纵坐标为

(4)

M′n的横、纵坐标为

(5)

平地直线OMn上任意点Mn-1的横、纵坐标为

(6)

在上坡面与点Mn-1相对应的点M′n-1的横、纵坐标为

(7)

图1 上坡方向平-坡坐标转换示意图Fig.1 Sketch of coordinate transformation from flat ground to sloping land in uphill direction

2.2.2下坡方向坐标转换

(8)

M′m的横、纵坐标为

(9)

平地直线OMm上任意点Mm-1的横、纵坐标为

(10)

在下坡面与点Mm-1相对应的点M′m-1的横、纵坐标为

(11)

图2 下坡方向平-坡坐标转换示意图Fig.2 Sketch of coordinate transformation from flat ground to sloping land in downhill direction

2.3 平地水量向坡地上的转换

2.3.1上坡方向水量转换

由沿喷头射流方向总水量守恒原理可知，平地直线OMn上的水量与上坡面直线OM′n上的水量相等，因此可将平地直线OMn上的水量折算到上坡面直线OM′n上。引入折算系数λ，上坡方向水量折算系数λup为

(12)

平地上的喷灌水量是已知的，假定平地直线上点Mn处和任意点Mn-1处的喷灌强度分别为Pn和Pn-1,则上坡面对应点M′n处的喷灌强度P′n为

(13)

任意点Mn-1在上坡面对应点M′n-1处的喷灌强度P′n-1为

(14)

2.3.2下坡方向水量转换

同上，下坡方向水量折算系数λdown为

(15)

假定平地直线上点Mm处和任意点Mm-1处的喷灌强度分别为Pm和Pm-1,则下坡面对应点M′m处的喷灌强度P′m为

(16)

任意点Mm-1在上坡面对应点M′m-1处的喷灌强度P′m-1为

(17)

通过上述方法，可将实测平地径向射线上的水量转换到坡地上，进而获得整个坡面上的水量分布。

2.4 模型的计算

应用Eclipse作为开发工具，对坡地喷灌水量分布计算进行程序化处理，图3为喷灌水量分布由平地向坡地转换计算程序流程图。

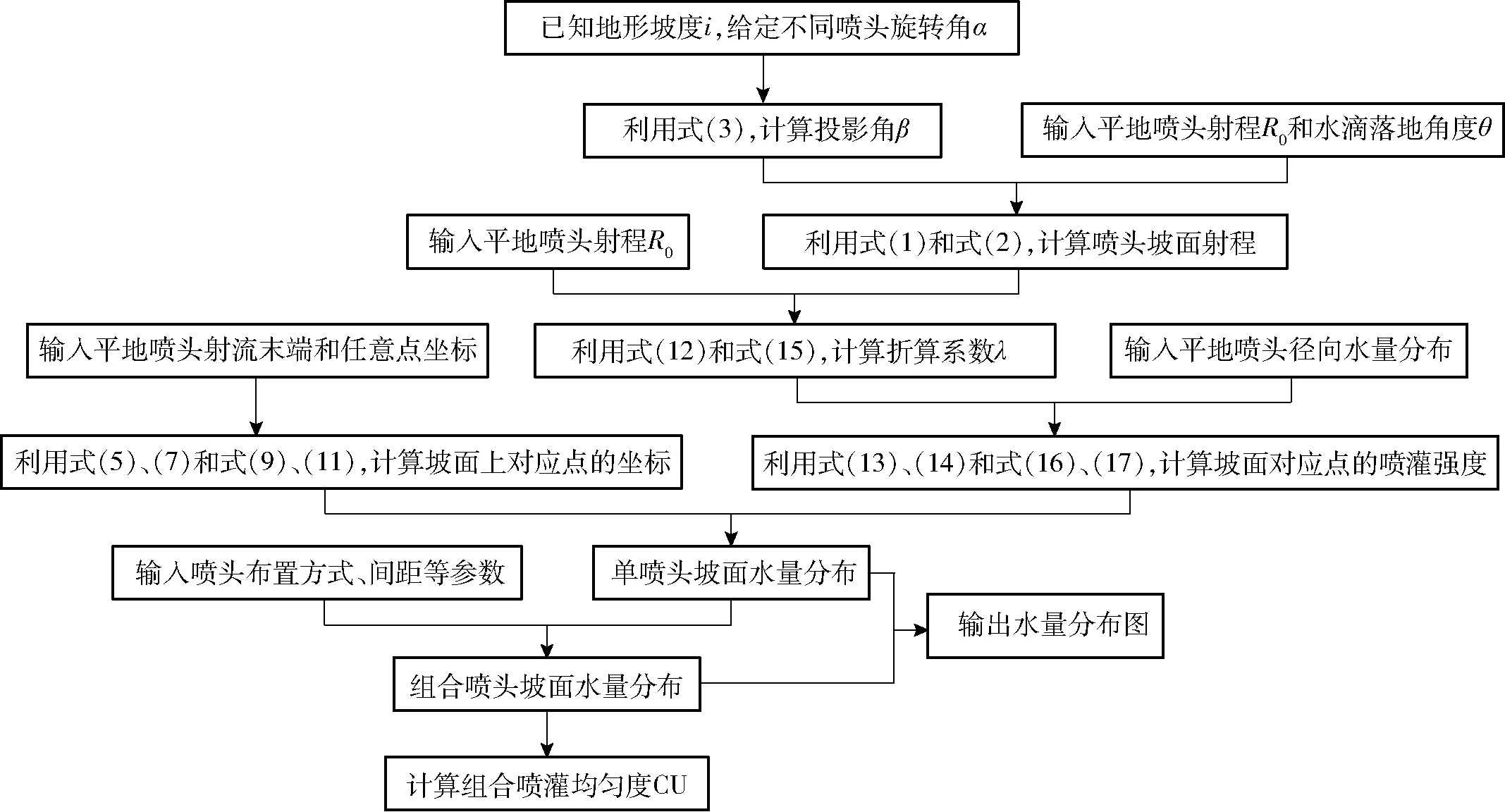
图3 喷灌水量分布由平地向坡地转换计算程序框图Fig.3 Programming flow chart for transforming sprinkler water distribution from flatground into sloping land

3 模型验证

3.1 验证试验

为了验证水量分布转换模型的正确性，在西北农林科技大学灌溉水力学实验厅测试单喷头在不同坡度和压力下的水量分布。试验装置由高度可调支架和钢槽、雨量筒、压力传感器、变频恒压供水节能控制柜、加压泵、不锈钢水箱、PVC管和阀门等组成，如图4所示。

图4 坡地喷灌水量分布试验装置图Fig.4 Experimental setup for sprinkler water distribution on sloping land1.雨量筒 2.钢槽 3.高度可调节支架 4.压力传感器 5.挡水薄膜 6.喷头

测试喷头为雨鸟LF1200型喷头，喷嘴尺寸为2.18 mm，喷射仰角为17°，工作压力范围为170～410 kPa。喷灌的地形坡度通过高度可调支架和宽0.15 m的钢槽实现，试验前，根据拟试验的坡度，计算不同控制点的高程，调节可调支架高度，将钢槽架设在支架上，进而形成试验所需的坡面。为了减小坡长，降低坡高，便于试验操作，将测试喷头分别铅直布置于坡面底端和顶端，安装高度为30 cm(厂家推荐的安装高度)。试验时，先将喷头布置于坡面顶端，记录其向下坡喷洒的水量分布，然后在压力等其他试验条件完全一样的情况下，再将喷头布置于坡面底端，记录其向上坡喷洒的水量分布，将上坡和下坡的水量分布数据合在一起即为该喷头在整个坡面上的水量分布。为了防止喷头喷洒出的水滴四处乱溅，损坏其他试验设备，在喷头周围安装一道弧形挡水薄膜。压力传感器为西安新敏CYB型(量程为0～500 kPa，精度0.1%)，将其安装在喷头进口处，并用防水塑料袋包裹，压力传感器与采集器连接，每隔5 s采集一次压力数据，最后求平均值。雨量筒高度为14.0 cm，开口直径为10.6 cm，将雨量筒布置在钢槽中，采用网格线法布置，网格在地面上的投影间距为1 m×1 m，共布置12行，每行11个雨量筒，共布置121个，观测记录雨量筒中水的体积，并转换成水深，从而获得每个测点处的喷灌强度(测点水深与喷灌时间的比值)。

试验因素为喷头工作压力和地形坡度。在厂家推荐喷头工作压力范围内选3个水平，分别为200、300、400 kPa，地形坡度有3个水平，分别为0.05、0.10、0.15，共测试9组，每次测试1 h，每组重复3次，每个测点处的喷灌强度取3次测试的平均值。

3.2 模拟与实测结果对比分析

限于篇幅，选择其中3组(压力200 kPa、坡度0.05；压力300 kPa、坡度0.10；压力400 kPa、坡度0.15)实测水量分布与模拟结果进行对照，将这3组分别记为P200I0.05、P300I0.10和P400I0.15。图5给出了模拟与实测水量分布的对照结果。坐标(0，0)为喷头位置，纵坐标正方向为坡面的上坡方向，纵坐标负方向为坡面的下坡方向。

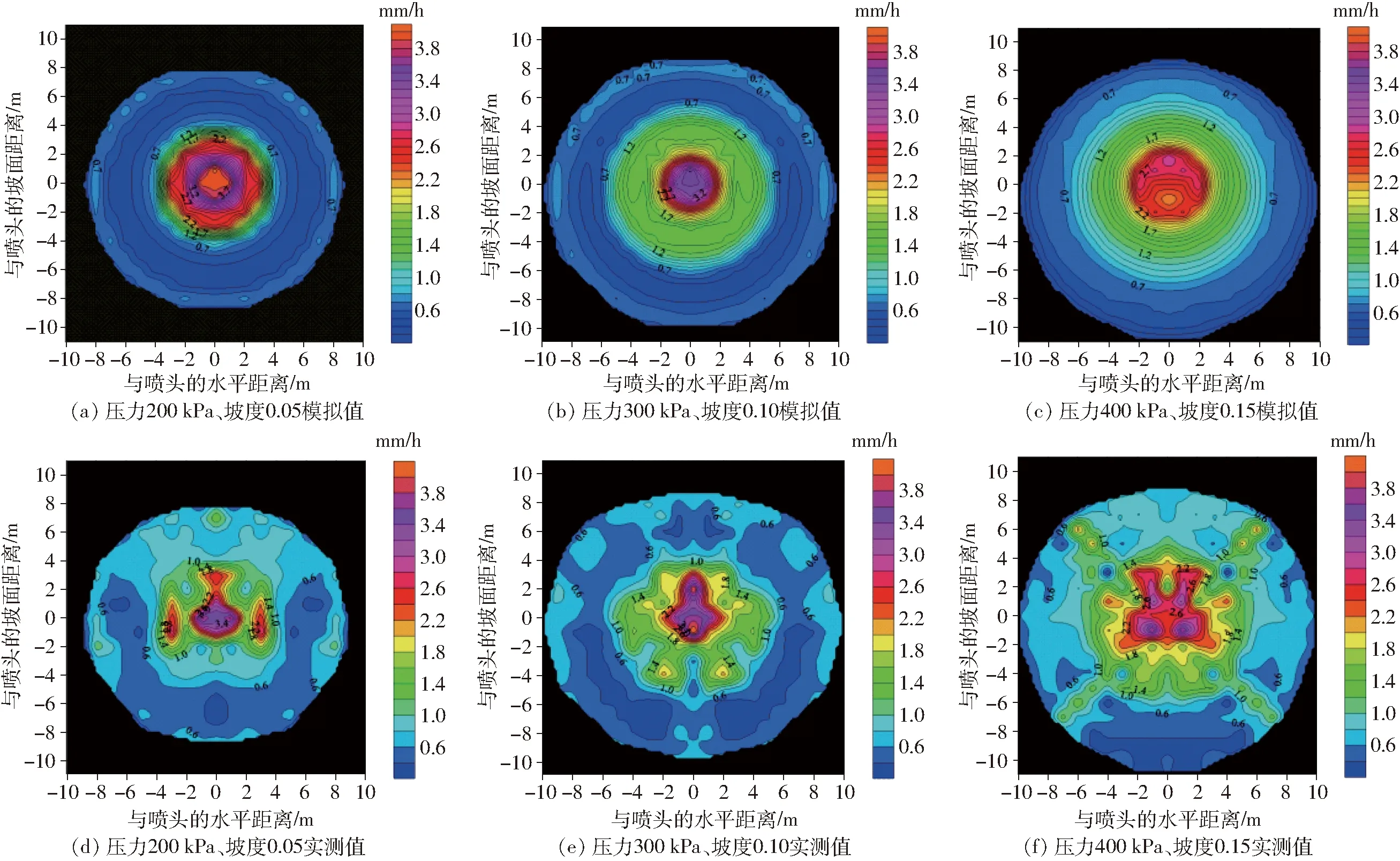
图5 单喷头水量分布模拟值与实测值对比Fig.5 Comparisons of simulated and measured water distributions for single sprinkler

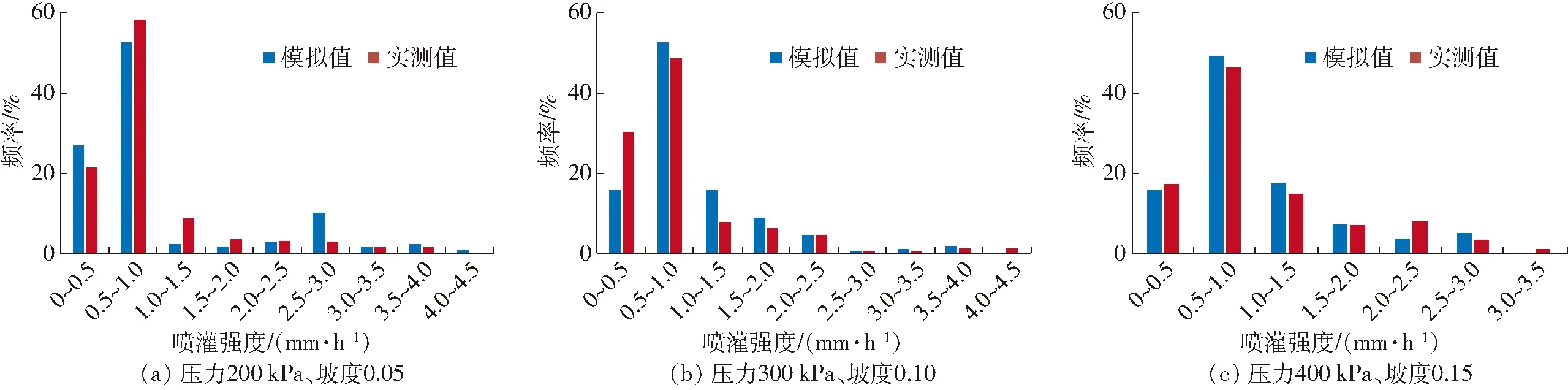
图6 模拟与实测喷灌强度频率对比Fig.6 Comparison of simulated and measured spray intensity frequency values

从水量分布图来看，模拟与实测的水量分布图形均为“鸡蛋形”，上部扁而宽，下部长而尖。从水量分布规律来看，模拟与实测的水量分布均为喷头附近水量较多，远离喷头水量较少，上坡方向水量相对集中，下坡方向水量相对稀疏。从喷灌强度峰值来看，模拟的3组(P200I0.05、P300I0.10、P400I0.15)喷灌强度峰值分别为4.05、3.65、2.91 mm/h，实测的分别为3.97、3.98、3.29 mm/h，其相对偏差为2.20%、8.32%和11.47%。从喷灌强度平均值来看，模拟的3组(P200I0.05、P300I0.10、P400I0.15)喷灌强度平均值分别为1.00、0.96、0.98 mm/h，实测的分别为0.91、0.87、1.05 mm/h，其相对偏差为10.30%、10.20%和7.12%。

图6给出了模拟与实测的喷灌强度频率的对比情况。从图中可以看出，模拟的不同压力和坡度下各级喷灌强度的频率与实测值基本吻合。综上，总体而言，模拟结果能够较好地反映坡地喷灌水量分布规律。模拟与实测结果之所以出现差异，一是因为坡地喷头射程公式计算出的坡面射程与实测值之间有一定误差，二是喷灌水量由平地转换到坡地时，采用了均匀折算。

4 模型应用

4.1 喷头布置方式对坡面水量分布的影响

图7 不同喷头布置方式下组合喷头坡面水量分布Fig.7 Water distributions for combined sprinklers with different sprinkler layouts on sloping land

图8 不同喷头间距下组合喷头坡面水量分布Fig.8 Water distributions for combined sprinklers with different sprinkler spacings on sloping land

图7给出了喷头工作压力为300 kPa、间距为R0、坡度为0.15时2种布置方式(方形和三角形)下组合喷头坡面水量分布情况。在方形布置下，4个喷头分别位于方形4个顶点，如图7a所示，在喷头附近和方形喷洒区域中偏下位置的圆环上水量分布较多，其各点喷灌强度均大于3.1 mm/h，且该区域占整个方形喷洒区域面积的43.8%；相邻两喷头之间的水量分布相对较少，尤以方形上部两喷头之间的水量最少，这是因为方形上部两喷头之间的水量主要是以单喷头下坡水量叠加而成，而单喷头下坡水量分布较上坡稀疏。在三角形布置下，3个喷头分别位于三角形3个顶点，如图7b所示，喷头附近水量分布较多，三角形喷洒区域中的其他地方水量相对较少。另外，方形和三角形布置方式下的组合喷灌均匀度CU(用Christiansen方法[19]计算)分别为84.2%和86.0%，三角形布置的CU略高于方形布置，说明三角形布置更利于坡地单喷头水量分布的叠加。因此，在坡地喷灌系统设计时，若仅从喷灌均匀性角度考虑，建议优先采用三角形布置方式。

4.2 喷头间距对坡面水量分布的影响

图8给出了喷头工作压力为300 kPa、坡度为0.15、三角形布置方式下不同喷头间距对坡面水量分布的影响。从图8中可以看出，不同间距下喷头附近水量较多，且随着喷头间距的增大，水量分布越来越不均匀，4个喷头间距下(0.8R0、R0、1.2R0、1.4R0)的组合喷灌均匀度CU分别为88.7%、86.0%、80.4%和77.1%。当喷头间距为0.8R0时，虽然组合喷灌均匀度CU高达88.7%，能满足喷灌质量要求，但是较小的喷头间距，将会增加喷灌系统中的喷头数量，导致系统成本上升。因此，在坡地喷灌系统设计时，若选用雨鸟LF1200型喷头，综合考虑喷灌均匀性和系统成本两个因素，建议喷头间距选用1.0～1.2倍平地喷头射程为宜。

4.3 坡度对坡面水量分布的影响

图9给出了喷头工作压力为300 kPa、间距为R0、三角形布置方式下坡度对组合喷头坡面水量分布的影响。从图9中可以看出，不同坡度下的组合喷洒水量分布极为相似，均是三角形下部两喷头附近水量分布较多，其他地方水量相对较少，这与单喷头水量分布叠加有关，三角形下部两喷头附近水量主要是由单喷头上坡水量叠加而成，而上坡水量分布较下坡水量分布集中，尤以上坡喷头附近水量最多。另外，随着坡度的逐渐增大，组合喷灌均匀度CU有所降低，坡度为0.10、0.20和0.30所对应的CU分别为86.1%、84.5%和82.0%，均能满足喷灌均匀性要求，说明在一定坡度范围内，地形坡度对坡面水量分布及组合喷灌均匀度的影响较小，因此在实际坡地喷灌系统设计时，当地形坡度不是特别陡峭时，应重点考虑喷头工作压力、间距和布置方式等其他参数的选取。

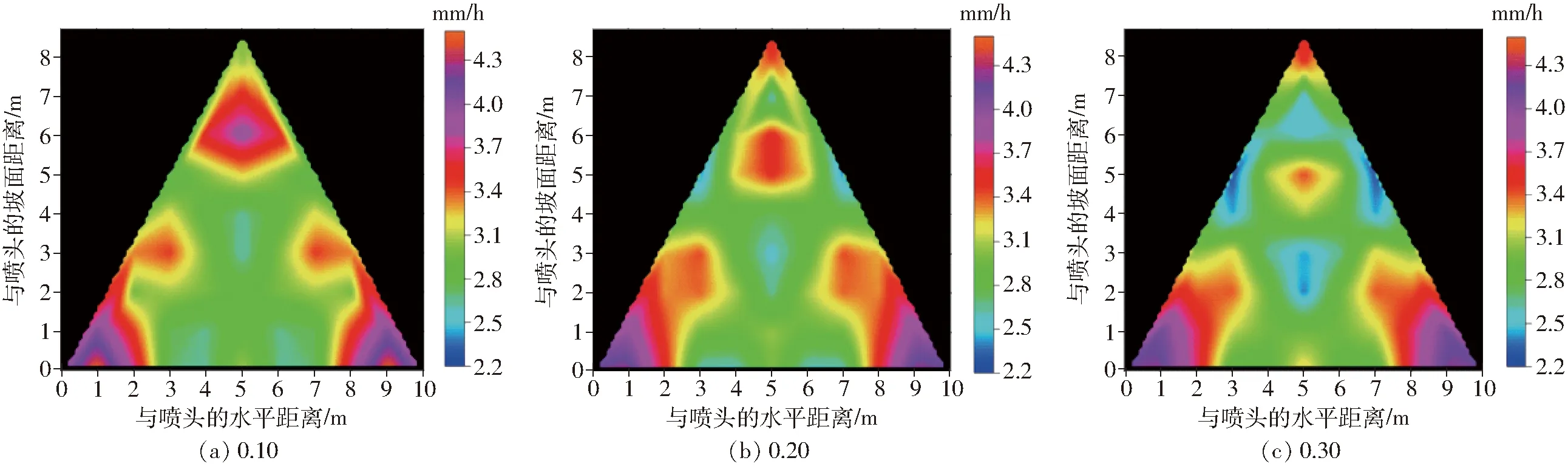
图9 不同坡度下组合喷头坡面水量分布Fig.9 Water distributions for combined sprinklers under different slopes

图10 不同喷头工作压力下组合喷头坡面水量分布Fig.10 Water distributions for combined sprinklers with different sprinkler pressures

4.4 喷头工作压力对坡面水量分布的影响

图10给出了喷头间距为R0、坡度为0.15、三角形布置方式下不同工作压力对组合喷头坡面水量分布的影响。从图10中可以看出，当喷头工作压力为100 kPa时，其水量分布极不均匀，喷头附近水量较多，其喷灌强度可达到2.8 mm/h以上，三角形中部水量普遍较少，其喷灌强度基本处于1.0～2.8 mm/h之间，且CU仅为44.6%；随着喷头工作压力的逐渐增大，当工作压力为200 kPa时，喷头附近喷灌强度在2.8 mm/h以上的区域增大，占整个三角形喷洒区域的比例达到56%，较工作压力为100 kPa时增加了16%，CU虽有所增加，达到64.5%，但仍低于国家《喷灌工程技术规范》中规定的75%的标准[20]，不能满足灌溉要求。因此，从灌溉质量考虑，不建议雨鸟LF1200型喷头在低压下运行。当喷头工作压力增大至300 kPa时，水量分布相对均匀，CU达到86.0%，均匀度较高，能够满足灌溉要求。当喷头工作压力进一步增大至400 kPa时，水量分布更为均匀，且CU高达89.7%。虽然更高的工作压力有助于提高喷灌均匀性，但是工作压力的增大意味着喷灌系统运行费用的上升，因此综合考虑喷灌均匀性和经济性，在坡地喷灌系统设计时，建议雨鸟LF1200型喷头工作压力选用300 kPa较为合适。

5 结论

(1)以坡地喷头射程计算公式为基础，根据喷头射流方向总水量守恒原理，构建了喷灌水量分布由平地转换到坡地的计算模型，且模型模拟的水量分布与实测水量分布基本吻合，其相对偏差在10%左右，说明该模型具有一定的准确性，模拟结果能够较好地反映坡地喷灌水量分布规律。

(2)基于雨鸟LF1200型喷头，应用该模型分别研究了喷头布置方式、喷头间距、地形坡度和工作压力等因素对坡地喷灌水量分布和组合喷灌均匀度的影响，结果表明，三角形布置下的喷灌水量分布均匀性略高于方形布置；随着喷头间距的增大，组合喷灌均匀度呈下降趋势；低压条件下，组合喷灌均匀度相对较低，不能满足灌溉质量要求，随着喷头工作压力的增大，组合喷灌均匀度逐渐增大；一定坡度范围内，坡度对坡面喷灌水量分布和组合喷灌均匀度的影响较小。

(3)在坡地喷灌系统设计时，若选用雨鸟LF1200型喷头，建议喷头布置方式优先选用三角形，喷头间距宜选用1.0～1.2倍的平地喷头射程，且喷头工作压力不易过低，应在厂家推荐的工作压力范围内选用300 kPa为宜。