基于有限元法的变压器振动噪声研究

2018-07-27胥建文徐莲环王新兵鲁文波程军卫

山东电力技术 2018年5期

胥建文，徐莲环，王新兵，鲁文波，程军卫

（1.山东电力设备有限公司，山东济南 250011；2.上海海基盛元信息科技有限公司，上海 200235）

0 引言

近年来，由于工农业生产和居民用电量的不断增长，城市用电负荷密度越来越大，随着城市规模的不断扩大及城区电网建设的需要，变压器的安装地点越来越靠近城区和居民区，许多大容量变电站陆续建设在市区内，中小容量变压器被广泛安装于居民区，使得变压器引起的振动和噪声问题日益突出［1-3］。

变压器的振动包括铁芯振动和绕组振动，铁芯的振动主要是由磁致伸缩力产生，而绕组的振动是由电磁力产生。绕组电磁力产生的振动可以通过有限元分析软件进行仿真计算，而铁芯磁致伸缩力产生的振动目前还无成熟的软件可用。

基于有限元和自编程相结合的方法对变压器的振动和噪声进行系统的分析与研究。根据磁致伸缩原理，编制了铁芯磁致伸缩力的计算程序，该程序可以对变压器和电抗器铁芯振动进行求解，进而分析整机振动噪声。

1 磁致伸缩

1.1 基本原理

铁磁材料在外磁场的激励下，其形状尺寸会随磁场的大小和方向发生变化，产生伸长/缩短的现象，这一现象被称为磁致伸缩。磁致伸缩是铁磁材料的一种固有属性，受诸多因素影响，如铁磁材料（一般是硅钢片）的成分，硅钢片轧制方向与磁化方向，硅钢片表面涂层，硅钢片热处理工艺，硅钢片表面应力，硅钢片装配方式等［4-6］。因此，受上述诸多因素的影响，即使是同一流水线上生产出的硅钢片，其磁致伸缩的规律也不尽相同。

为了衡量材料磁致伸缩的大小，类似于材料应变的概念，人们定义了磁致伸缩率λ，即在外磁场作用下，铁磁材料的伸长量（Δl）与自身原长L的比值，λ=Δl/L。磁致伸缩率λ是关于磁场大小和方向的函数，受诸多因素影响，很难完整地建立一个理论模型，一般借助实验手段，直接测量铁磁材料的磁致伸缩率λ。典型的磁致伸缩测量仪如图1所示，为了提高测量精度，一般采用激光位移计进行磁致伸缩量的测量。

图1 磁致伸缩测量仪

通过对不同磁场作用下的磁致伸缩量进行测量，便可得到一系列磁通密度与磁致伸缩率之间的对应关系，将这些数据绘制成曲线并进行合理拟合，便得到磁致伸缩率曲线，典型的磁致伸缩率曲线如图2所示。

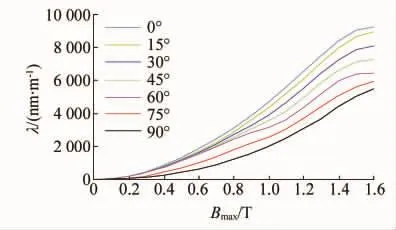
图2 磁致伸缩率曲线

虽然磁致伸缩是铁磁材料的一项固有属性，但人们更习惯于把磁致伸缩看成是在某种外力作用下发生的变形，这种外力其实是一种等效力，被称为磁致伸缩力Fms。也就是说，在磁致伸缩力Fms的作用下，铁磁材料的变形与其磁致伸缩产生的变形相同。

1.2 磁致伸缩力计算

在有限元模型中，单元的磁致伸缩率λe（等效于应变）可由磁致伸缩率曲线和节点磁通量密度B确定。一般认为，磁致伸缩不会改变铁磁材料的体积，即在笛卡尔坐标系中，单元体积不变，即

式中：λex，λey和 λez分别为单元沿 x，y，z轴的应变（磁致伸缩率）。已知沿磁化方向（假定为沿x轴方向），铁磁材料单元的应变为λex=λ（即为磁化方向上的磁致伸缩率，通过实测得到），则单元另外两个方向的应变为

根据单元应变 λex，λey和 λez，可根据结构力学的相关理论计算单元节点上的磁致伸缩力Fms。

2 多物理场耦合

电力变压器的振动及噪声是典型的多物理场耦合问题，分别涉及磁固耦合、流固耦合和声固耦合。

2.1 磁固耦合

首先采用瞬态场进行磁场计算，获取铁芯硅钢片上交变磁场数据，然后计算出交变磁场产生的磁致伸缩力。将磁致伸缩力进行FFT变换，得到不同频率下的激振力。在结构分析中，基于振动微分方程，采用时谐场分析方法，将不同频率下的激振力作为边界条件，施加到结构模型中进行振动计算。结构振动分析所需的主要的微分方程为［7］

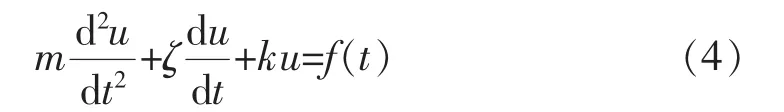
式中：m为质量；ζ为阻尼比；k为刚度；f为激振力；u为振动位移。

2.2 流固耦合

对于油浸式电力变压器，变压器油也是振动传递的一条关键路径。因此，流固耦合是研究油浸电力变压器的一项关键技术。耦合问题，分为强耦合和弱耦合，油浸式电力变压器的振动属于强耦合，因为变压器油一方面作为介质传递振动，另一方面作为附加质量和阻尼，抑制振源的振动。强耦合的数学表达为［8］

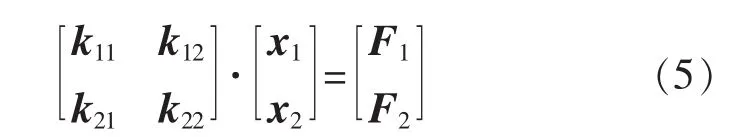
式中：F为边界条件；x为自由度（振动位移）；k为材料相关的参数（刚度矩阵）。

油固耦合问题的求解应在结构分析中进行，在结构振动计算模型中采用流固耦合单元来模拟变压器油对振动的影响，该单元的自由度为压力，一方面产生并传递由铁芯振动引起的压力场波动，另一方面其产生的压力作用于结构模型的边界而影响结构振动。

2.3 声固耦合

油浸式电力变压器的噪声是油箱表面的振动向外辐射的效果，这种耦合属于弱耦合，即油箱表面上的振动会影响噪声的大小及分布，但噪声并不对油箱表面上的振动产生影响。变压器油箱外表面的声压 p 满足 Helmholtz波动方程［9］：

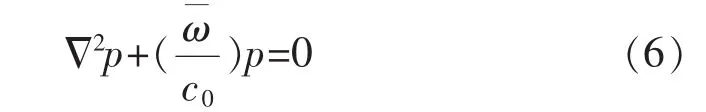
式中：p1、p2为声波的声压；u1n、u2n为声波的法向速度。即在分界面上，声波的声压和法向速度必须连续。

3 计算流程

计算流程如图3所示。

计算空载状态下铁芯的磁密分布，通过电磁的仿真，得到铁芯的磁密分布与大小，为磁致伸缩力的计算提供了数据支持。

通过在完成电磁场仿真以后，将铁芯网格节点处的磁密结果作为输入条件，利用自编程的磁致伸缩力计算程序作为工具，进行铁芯磁致伸缩力的求解。

通过磁致伸缩力的计算和洛伦兹力的提取，获得用于变压器电磁振动计算输入条件，为电磁振动的计算做好了准备。

通过模态试验，得到了变压器主要部件和整机的模态参数和振型图，可以为变压器的减振降噪提供参考。

将仿真结果与试验数据进行对比后，对仿真模型进行适当修正，修正后的模型重新进行模态仿真计算，得到结果应与试验结果具有较好的精度，以保证建模的合理性，从而提高振动噪声的计算精度。通过主要部件和整机模态的仿真计算与校核，逐步完成了变压器各部分的材料模型的修正。

将噪声的仿真结果与测试结果采用声功率级进行对比，声功率级的大小不受距离和障碍物影响。

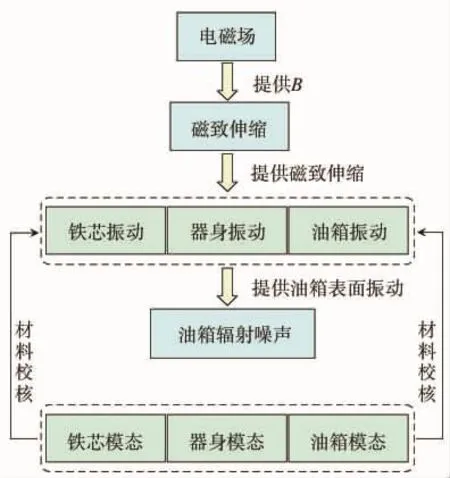
图3 计算流程

4 变压器的模态分析

4.1 基本原理

模态分析用于确定结构本身固有的振动特性，主要包括自振频率和振型，通过频率和振型的分布可以确定结构的薄弱环节，避免系统发生共振现象。

多自由度无阻尼系统的运动方程为［7，9］

在自由振动时f（t）=0，将此代入式（8）中，得到

设特解 x=Φejωt代入式（9）中得

该方程有非零解得充要条件是其系数矩阵行列式为零，即

解得ω的n个互异正根ω0i，成为无阻尼系统的固有频率（特征方程的特征值）。

将ω0i代入式（10）中，解得n个线型无关非零矢量φi的比例解，通常选择一定方法进行归一化，称为模态振型（特征方程的特征向量）。

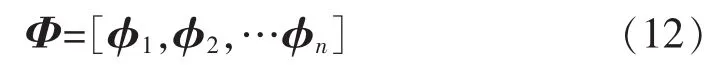
4.2 模态仿真

对变压器的铁芯和器身进行模态仿真计算，提取固有频率和振型，求解模型如图4、图5所示，模态仿真结果如图6所示。

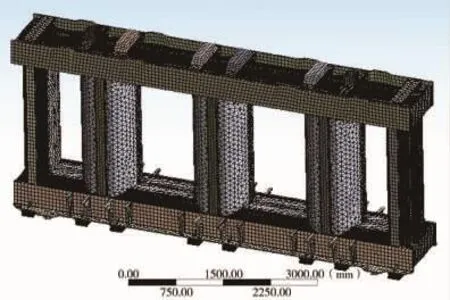
图4 铁芯有限元模型

图5 器身有限元模型

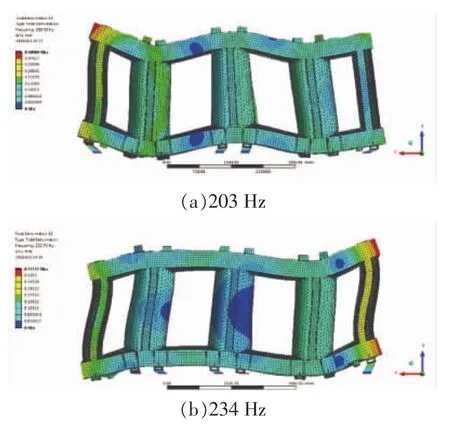
图6 不同铁芯固有频率下的模态振型

图6（a）是铁芯固有频率为203 Hz模态振型，铁轭表现为 W 型的弯曲；图 6（b）、图 6（c）、图 6（e）分别是铁芯固有频率为234 Hz、300 Hz、449 Hz的模态振型，这3个图主要表现为旁轭的S型或者C型弯曲；图6（d）是铁芯固有频率为395 Hz的模态振型，主要表现为C型弯曲。通过铁芯模态振型可以看出，上、下铁轭主要表现为S型或W型的弯曲模态；旁轭主要表现为S型的弯曲模态；由于3个铁芯柱的刚度较大，弯曲变形不明显。

4.3 模态测试

模态测试包括铁芯模态、器身模态和油箱模态，油箱的模态振型丰富，固有频率点多，这里不列出，只对铁芯和器身进行对比分析。进行模态测试时设置的试验参数如表1所示，图7所示为器身模态测试的频响函数和稳态图，铁芯测试现场传感器布置图如图8所示，器身测试现场传感器布置图如图9所示。

表1 模态试验参数

4.4 仿真与测试对比

将铁芯和器身模态的仿真值与实测值进行对比，平均误差控制在10%以内，具体结果对比如表2、表3所示。

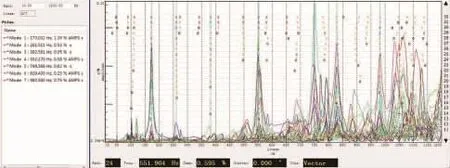
图7 模态测试

图8 铁芯测试现场

图9 器身测试现场

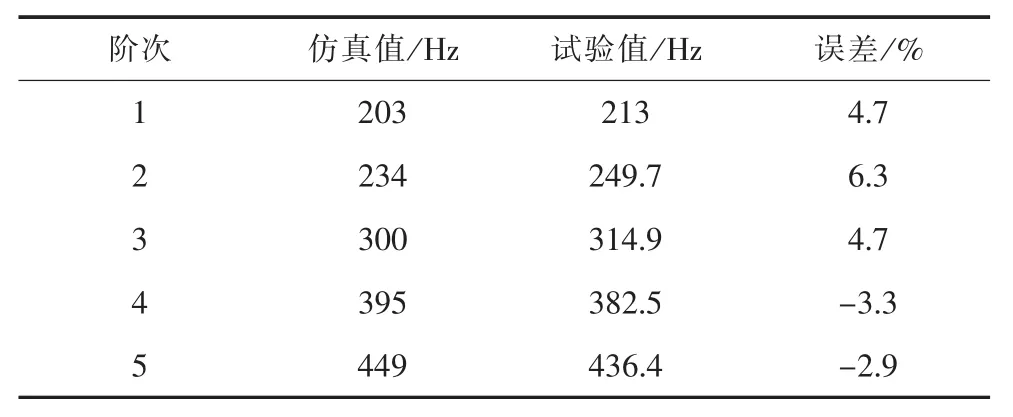
表2 铁芯模态频率对比

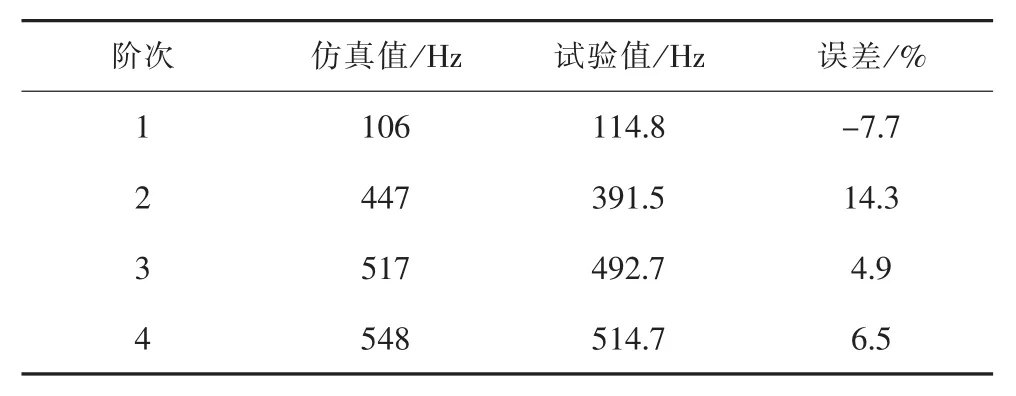
表3 器身模态频率对比

5 变压器的振动与噪声分析

5.1 基本原理

油浸式变压器的噪声相当于油箱各个面声源的辐射，而各面声源可以应用点源（小脉动球源）的组合来近似处理。脉动球源是进行着均匀涨缩振动的球面声源，在球源表面上各点沿着径向作同振幅、同相位的振动。这种情况下可以运用特殊形式的波动方程式，即

将小球面积S=4πr2代入上式，则成为

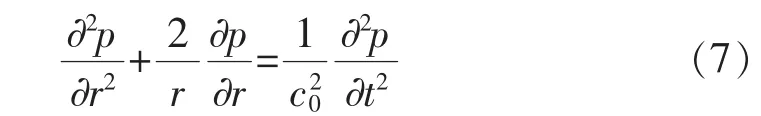
令 Y=pr，那么式（7）就可化为

可以求得式（8）的一般解为

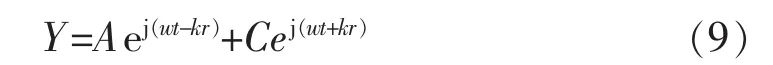
式中：A和B为两个待定常数。

解得Y即可求得式（7）的一般解为

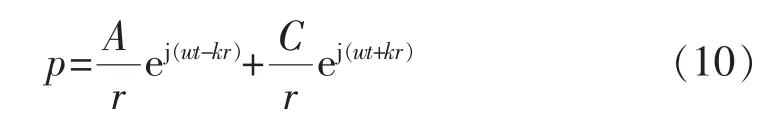
式（10）的第一项代表向外辐射（发散）的球面波；第二项代表向球心反射（会聚）的球面波，现在讨论无界空间辐射的自由行波，因而没有反射波，这里常数C=0。这样式（10）就成为

5.2 振动和噪声仿真

图10 变压器整机模型

建立变压器的整机模型，包括铁芯、绕组、拉板、夹件、变压器油、油箱及其附属的结构件，然后将磁致伸缩力和绕组电磁力的计算结果映射到整机模型中，对变压器整机振动进行仿真计算。计算模型如图10～11所示，振动结果如图12所示。

图11 整机有限元模型

图12（a）～（e）所示为 100 Hz～500 Hz 下的振动分布图，给出了不同频率下振动的位移，其目的一方面是为了仿真与试验数据进行对比，另一方面是为噪声仿真分析提供振动源。

基于振动结果进行变压器的声辐射计算，得到声功率级结果如表4所示。

表4中最后一列为利用声压级实测值的数据，考虑所有频率后的总声功率级。各频率下声功率级差异较大的原因是：某些频率处激励力与器身或油箱固有频率较近而产生共振，导致振动噪声大。变压器噪声是基于单频振动结果计算的，看不同频率下的声功率级能体现变压器噪声的频谱特性。

总声功率级计算公式为

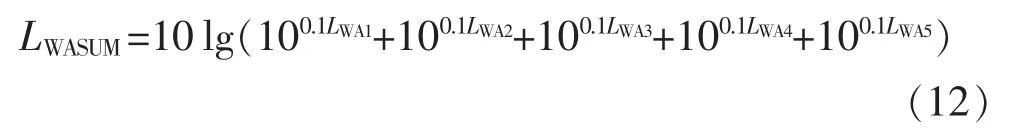
式中：LWASUM为总声功率级；LWA1为100 Hz频率下的声功率级；LWA2为200 Hz频率下的声功率级；LWA3为300 Hz频率下的声功率级；LWA4为400 Hz频率下的声功率级；LWA5为500 Hz频率下的声功率级。

通过下述公式对声功率级进行计算，得到声功率的计算值为85.37dB（A），与仿真值的误差为0.2%，验证了变压器振动噪声仿真计算方法的准确性。

变压器的A计权声功率级为

式中：LWA为A计权声功率级；为修正的平均A计权声压级；S为测量表面面积；S0为基准参考面积。

修正的平均A计权声压级为

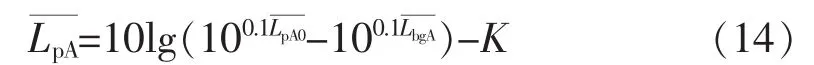
6 减振降噪优化方案

油浸式电力变压器振动量的传递主要有两个路径，一是通过垫脚将振动量传递给油箱，即固体传递；二是通过变压器油将振动量传递给油箱，即流体传递。固体传递常用的减振措施是在器身与油箱之间加不同厚度的减振垫，减振垫是一种阻尼材料，可以消耗固体传递路径上的振动量，但厚度增加到一定程度之后，振动量非但没有被降低，反而增大。表5分析了不同厚度减振垫作用下的声功率级。

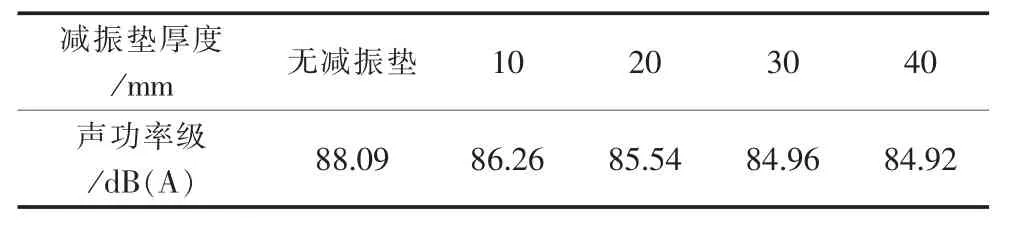
表5 不同厚度减振垫下的声功率级

从表5可看出，当减振垫的厚度逐渐增加后，变压器的声功率级也随之降低，下降的最大差值为3 dB，减振垫的方案只能使变压器的声功率级降低3 dB。如果想继续降低变压器的噪声，只能从其他方面着手。在油箱结构上做4种减振降噪的优化方案，如图13所示，具体说明如表6所示，相应声功率级结果如表7所示。

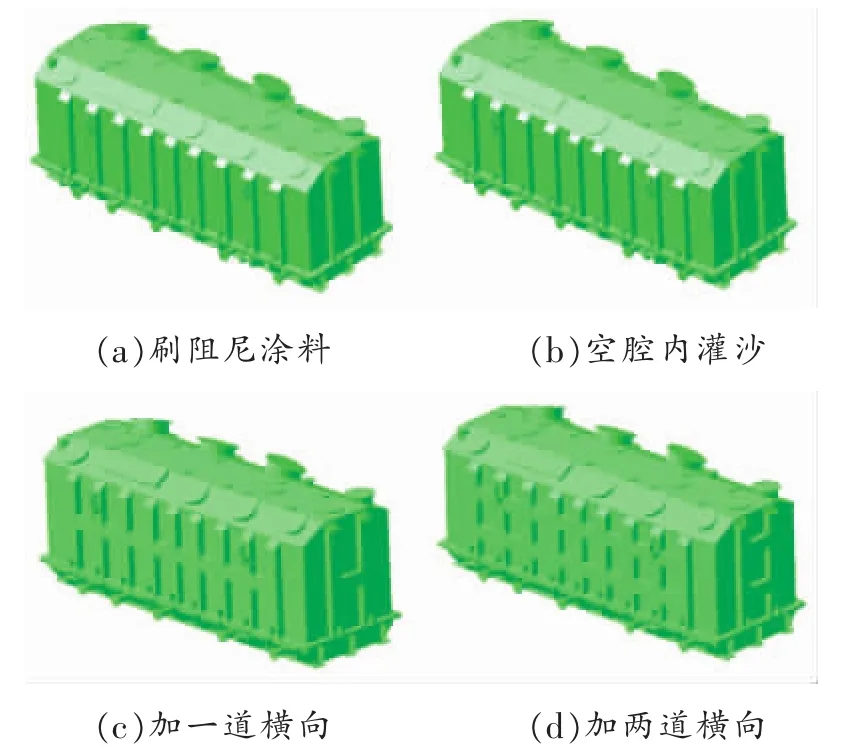
图13 降噪方案

表6 优化方案说明

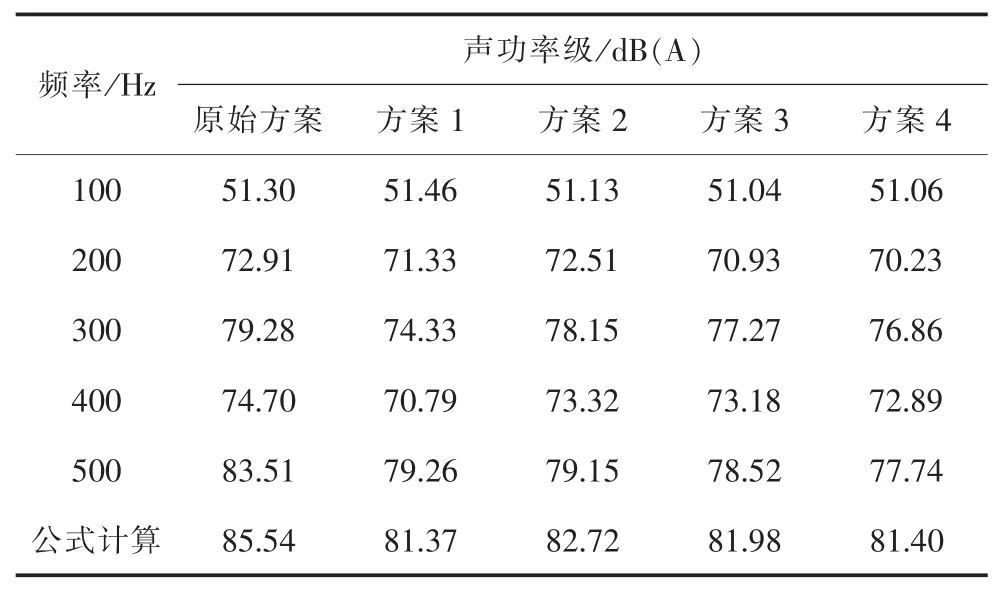
表7 不同方案下变压器的声功率级

通过表7中声功率的仿真结果可以看出，油箱外表面涂刷阻尼涂料的方案1可以使声功率级降低4.17 dB，油箱各侧壁的空腔内灌沙的方案2可以使声功率级降低2.82 dB，油箱各侧壁加一道加强筋且空腔内灌沙的方案3可以使声功率级降低3.56 dB，油箱各侧壁加两道加强筋且空腔内灌沙的方案4可以使声功率级降低4.14 dB。