特征层双模态生物识别算法容侵能力评测方法

王志芳, 甄佳奇, 朱福珍, 宋建华

(黑龙江大学电子工程学院, 黑龙江 哈尔滨 150080)

0 引 言

随着信息技术的快速发展,人们进入了数字化和网络化的时代,个人身份信息也随之数字化和隐性化[1]。个人身份信息越来越多的关系到个人隐私、财产安全与社会的公平和秩序,因此快速、准确、安全地在数字化环境中进行个人身份识别与验证成为信息安全领域研究热点之一,具有重要的理论意义和实用价值[2-3]。传统身份认证方式无法实现身份标志信息或物品与用户本人的唯一关联性和不可分离性,而生物识别技术将人体生物特征作为身份标志,兼顾了系统安全和用户体验,因此在信息安全等领域受到了广泛关注。随着生物识别技术在各个领域的广泛应用,单模态生物识别暴露了诸多问题,而多模态生物识别技术具有更优的适用性、安全性和可靠性,成为目前生物识别技术发展的趋势[4],也为信息安全应用系统提供了更加安全和可靠的身份认证方案。

根据融合发生的阶段不同,多模态生物识别方法具体划分为4个层次,分别为像素层、特征层、分数层和决策层[5]。相比像素层融合,特征层融合实现了信息的客观压缩,规避了大量数据的计算,有利于实时处理;而分数层和决策层就是将多个匹配分数和决策按照某种规则进行融合综合判断给出最终的结论。而融合的匹配分数和决策均来自单模态生物识别系统,这使得分数层和决策层的性能依赖于单模态生物识别系统,提升系统性能的空间有限[6-7]。而特征层融合提取决策分析所需的最大区分性类别信息,在理论上可得到最优识别效果。因此,特征层融合算法是多模态生物识别技术中一个潜力很大的研究方向,相关文献也陆续出现[6-8]。

目前,关注多模态生物识别技术安全问题的研究者并不多,仅有的少数文献提及也是与单模态生物识别技术相同的通识问题,而关于特征层多模态生物识别安全问题的研究更鲜有出现。目前,特征层多模态生物识别技术多以双模态生物识别算法为主。本文从双特征入手,将入侵容忍的概念引入到特征层双模态生物识别技术的安全评测中。对于一个系统来说,入侵是在没有授权的情况下,对系统资源进行存取、处理或破坏以使系统不可靠、不可用的故意行为[9]。从特征的角度来考虑,对于单模态生物识别来说,入侵行为就是窃取或伪造生物特征,这意味着该特征已经泄露,攻击者可以利用该特征进入系统获取所要的信息,系统安全和用户隐私将无法保障[10-12]。对于双模态生物识别技术来说,当所有模态的特征泄露时与单模态生物识别相同,攻击者就可以合法地进入系统。但双模态生物识别还存在另一种情况,只是一种生物特征泄露,也就意味着攻击者拿到了一种真实的生物特征。此种情况下,系统是否应该承认攻击者的合法身份,毕竟一种生物特征是真实的？但另一种生物特征并不是真实的,系统给予的判断结果应该是两种特征综合分析的结果。对于此种情况的讨论,本文借用入侵容忍技术。入侵容忍主要考虑在遭到攻击的情况下系统的可生存性,关注的重点是入侵造成的影响而不是入侵的原因[9, 13]。所谓的可生存性是指系统被部分入侵、性能下降的情况下,还能维持系统正常服务的能力。对于双模态生物识别技术,当一种特征被窃取,另一种特征并不真实的情况下,本文提出了容忍能力评测方案,比较典型特征层双模态生物识别算法的可生存性。

1 问题提出

根据入侵容忍的概念,多模态生物识别系统的可生存性是指在生物特征被窃取的情况下,还能够正确判定用户的身份。给出判定结果需要一个比对的过程,也就是需要将测试样本特征与数据库中的模板特征进行匹配。而由于生物特征具有模糊性,也就是采集的生物样本每次都不可能完全一样,比如指纹每次按压的力度、角度做不到完全一样,人脸不同时刻拍照时的表情,姿态也做不到完全相同,因此生物特征的匹配是采用阈值匹配,换句话说,2个生物特征之间的距离小于阈值被认为2个生物特征是来自同一个用户,大于阈值被认为2个生物特征来自不同的用户。在此基础之上,生物识别技术针对两种应用模式有两套对应的性能评价指标。

识别和认证是生物识别技术的两个应用模式[14]。识别是一对多的匹配,测试样本特征与注册的所有模板特征进行比对,按照某种距离测度给出识别结果。只要该测试样本特征与注册模板中的任意一个能够匹配,则识别成功,也就是所谓的一对多。反之,则认为识别失败。由此可见,识别模式强调的是身份的合法性,只要具有合法的身份,无论是否与用户自己的模板特征相匹配都可以得到系统的授权。验证模式则是一对一的匹配,测试样本特征必须与拥有该样本的用户注册的模板特征相匹配才被认为正确匹配,也就是验证成功。若测试样本特征与其他用户的注册模板相匹配,则被认为错误匹配,也就是验证失败。因此,验证模式是一对一的匹配,更适于算法性能的评价。

根据2种应用模式从而有了2对性能评价指标:错误接受率(false accept rate, FAR)和错误拒绝率(false reject rate, FRR),错误匹配率(false match rate, FMR)和错误匹配率(false non-match rate, FNMR)[14]。其中,FAR和FRR是针对识别模式,FMR和FNMR是针对验证模式。本文关注特征层双模态生物识别算法,因此选用FMR和FNMR两个性能参数。FMR和FNMR的计算需要将样本分为2个集合:用户的训练样本集和用户的测试样本集。则FMR和FNMR计算公式为

式中,样本类间距离是指不同用户特征之间的距离;样本类内距离是指同一用户特征之间的距离。

目前,多模态生物识别的研究多以双模态生物识别为主,也就是融合两种生物特征进行身份识别。本文以双模态生物识别算法为例,对入侵容忍问题进行分析。表1为双模态生物特征A和B不同情况下给出判定结果后所对应的评价性能参数。当2种特征都是真的,判定正确匹配,或者两种特征都是假的,判定错误匹配,这两种情况没有任何异议,用“√”来标记。若两种特征都是真的,当错误匹配时很显然应归属于错误误匹配率了,对应参数就是FNMR。同理,当两种特征都是假的而被判定正确匹配时对应的参数就是FMR了。这4种情况很容易归属,可当两种特征有真有假时,无论判定结果是正确匹配还是错误匹配,都很难去界定对应的参数,在表中用“√”表示。此时,相比单个用户的判定结果是否正确,整体算法的可生存性更引人关注。

表1 双模态生物特征真假分析

2 容侵能力评测方法

多模态生物识别的优势正是体现在这个“多”上面,多种生物特征的参与提高了系统的适用性、可靠性和安全性。然而,当其中一种模态的生物特征被窃取时,系统的识别性能会受到什么样的影响？系统的安全性会受到什么影响？目前几乎没有文献涉及过此问题,更没有给出定量的指标来评测这个问题。理想情况下,部分特征被窃取后融合算法尽可能地保持与无特征被窃取情况相同,这样能够保证攻击者即使得到用户的一种样本特征,与没有得到用户样本特征进入系统的难度大致相同,也就是系统还能基本完成系统功能。因此,部分样本特征被窃取情况对于多模态生物识别算法在区分性上有更高的要求,尽量避免出现错误匹配。本文从系统安全出发,关注FMR的变化程度,首先定义了FMR的积分差作为精确容侵能力度量,设计评测方案,对典型特征层双模态生物识别算法进行评测。

2.1 参数定义

从安全的角度来考虑算法的性能,用户更为关心攻击者攻破系统的可能性,对应的参数也就是FMR。因此,本文以FMR为性能评价参数,测试样本特征部分被窃取的情况下算法功能完成的情况,也就是算法容侵能力的测试。如何进一步定量的衡量算法的容侵能力,本文首先定义算法的安全威胁参数。

定义1某种多模态生物识别算法的安全威胁参数定义为

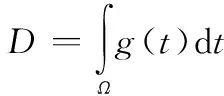
(1)

式中,t为匹配阈值;Ω为可能的匹配阈值的范围;g(t)为该算法的FMR曲线。

定义D实际上是计算FMR曲线在阈值范围Ω的定积分,相对于单一的某个阈值下的FMR,D更准确更全面地反映了识别算法的整体安全性。在实际计算中,阈值的取值是离散的,设阈值取值序列为x0,x1,…,xn,如图1所示,安全威胁参数可转化为

(2)

在实际测试中,在匹配之前已将融合特征进行了归一化,从而归一化匹配阈值的范围为[0,1]。

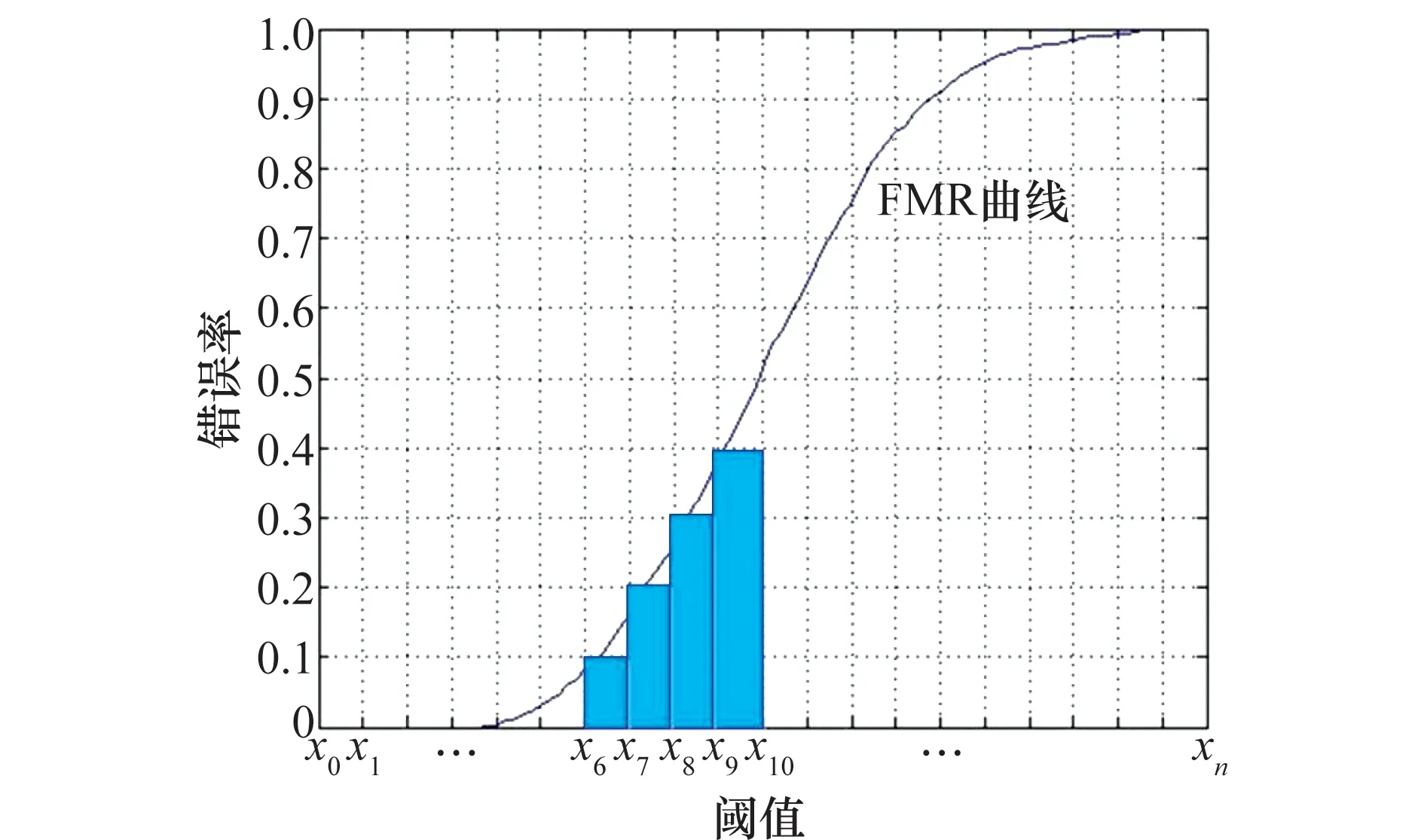
图1 离散安全威胁参数定义Fig.1 Definition of discrete security threat parameter

当样本特征部分被窃取时,攻击者拿到部分特征的情况下,希望融合算法还能够将攻击者识破,即要求融合算法在样本特征部分窃取情况下,FMR上升速度不能过快,仍然保持与正常情况相当的区分性。为了度量这一点,本文进一步提出了容侵能力度量准则。

定义2某种多模态生物识别算法的容侵能力度量定义为

(3)

式中,Dn和Dl分别表示正常情况下和样本特征部分窃取情况下该算法的安全威胁参数;gn(xi)和gl(xi)分别表示正常情况下和样本特征部分窃取情况下该算法的FMR曲线。实际上,V即为两种情况下FMR曲线之间的面积,如图2所示。

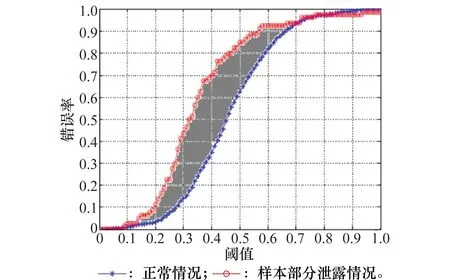
图2 容侵能力度量定义Fig.2 Definition of intrusion tolerance capability measurement

V反映了融合算法识别性能受样本特征部分窃取的影响程度,该值越小表示融合算法的容侵能力越高,等于0是容侵能力最佳的理想情况,即算法的性能不受样本特征被窃取的影响,该算法的安全性也就越高。上述2个度量的引入使得能够有效对融合算法的总体识别性能进行量化的评估,对融合算法在样本特征部分窃取情况下容侵能力下降程度进行定量的分析。

2.2 评测方案

3 实验结果

3.1 典型特征层融合算法

目前,特征层多模态生物识别技术多以双模态生物识别算法为主。因此,以双模态生物识别算法为例给出测试结果。传统的特征层双模态生物识别算法有两类:串联融合和加权融合[5-6]。串联融合就是将2种模态特征向量串联成一个长向量,这样带来的计算量非常可观。而加权融合是将2种模态特征向量分别乘以权值后再叠加,但权值的选择是个备受争议的问题。典型相关分析(canonical correlation analysis, CCA)属于并联方式,但与加权融合模式不同,并没有提前将2种特征进行融合,整个算法既是融合过程,也是分类过程[15]。复数融合是一种新兴的融合模式,其将2种模态特征向量分别作为实部和虚部组成复数特征向量,再对复数特征向量进行分类。这样既解决了串联带来的巨大计算量,同时又避免了权值的选择问题[16-20]。

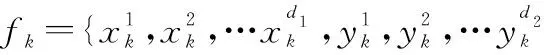
fk=

(4)

因此,根据式(4)得到的融合特征维数为d=max{d1,d2}。

CCA算法按照相同的方式统一特征维数,其通过2个数据集之间的线性变换来提取典型变量,利用典型变量间的相关系数来表征数据集间的相关性,从而找到两个投影方向使得两个数据集投影后具有最大的相关性。投影方向α和β的求解可通过式(5)的最大化得到。

(5)

式中,Sxy为训练样本集x和y的互协方差矩阵;Sxx和Syy分别为样本集x和y的协方差矩阵。

复数融合模式按照加权融合相同的方式统一特征维数,则复数融合方式的第k个融合特征fk为

(6)

式中,i为虚数单位。

通常情况下,串联融合和加权融合方式得到融合特征之后按照某种距离测度进行匹配从而得到验证结果,而CCA算法整体既是融合过程也是分类的过程。复数融合方式得到融合特征后还需要再利用复数分类器进行再次分类给出最后的验证结果。文献[16]最早提出复数融合并给出了复数Fisher鉴别分析算法(complex fisher discriminant analysis,CFDA)算法,利用复数向量融合使用不同特征提取方法得到的人脸特征进而分类识别。CFDA的目标函数为

(7)

式中,Sb和Sw分别为样本类间散度矩阵和样本类内散度矩阵;H为共轭转置符号。当wHSww=0且wHSbw≠0时,目标函数达到最大值。正是基于上述思想,复数普通向量(complex common vector, CCV)算法被提出[17],目标函数为

(8)

式中,St为总体散度矩阵。考虑到非线性特征的存在,基于核函数的复数双模态生物识别算法复数核主成分分析(complex kernel principal component analysis, CKPCA)和复数核Fisher鉴别分析(complex kernel fisher discriminant analysis, CKFDA)相继出现[18-19],算法的目标试图将原始训练样本通过某个非线性映射映射到某一高维特征空间,并在该空间中实现线性主成分分析和Fisher鉴别分析,目标函数分别为

(9)

(10)

式中,R=K-1mK-K1m+1mK1m,K为样本核矩阵,1m为m×m元素都为1的矩阵(m为样本总个数);Kb和Kw分别为基于核函数的类间散度矩阵和类内散度矩阵,本文测试采用高斯核函数。

复数局部保射投影(complex locality preserving projection,CLPP)算法是让原始样本同类的数据点间距离较近的点,在经过映射到低维空间后两点间的距离被压缩的很近,该方法能够很好地保持原始数据同类间的非线性结构,因此在经过映射后能够充分利用同类间的非线性结构保持其相似性[20]。这种映射克服了传统线性分析算法不能保留高维数据中流形结构的缺点,同时还克服了非线性映射后很难获得在低维样本空间上的简洁特征表示的困难。其目标函数为

(11)

式中,Sij表示互为近邻的两个数据点之间的相似度。

3.2 实验对象

本文采用中科院自动化所(Institute of Automation，Chinese Academy of Sciences, CASIA)公开虹膜数据库,奥利维提研究实验室(Olivetti Research Laboratory, ORL)人脸数据库和耶鲁(Yale)人脸数据库。CASIA虹膜数据库包括108个虹膜个体,每个虹膜分两个阶段采集7幅图像,共756幅虹膜图像。ORL人脸数据库由剑桥大学AT&T实验室创建,包含40人,每人采集10幅图像,共400幅人脸图像,其中包括了姿态、表情和面部饰物的变化。Yale人脸数据库由耶鲁大学计算视觉与控制中心创建,包含15人,每人采集11幅图像,共165幅人脸图片,同样包含光照、表情和姿态的变化。

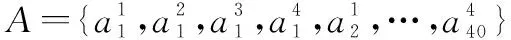
3.3 实验结果

对第3.1节中所述的特征层双模态生物识别算法进行评测:串联算法,加权算法,CFDA算法,CCV算法,CKPCA算法,CKFDA算法,CCA算法,CLPP算法。在加权算法中,由于虹膜识别相较于人脸识别在准确率方面性能更优,因此在权值分配上偏重于虹膜特征,以期望虹膜特征的区分性能在融合特征中起到重要作用,本文实验中2种特征的权值取为θ1=0.3,θ2=0.7。同时,也添加了加法算法的实验对比,将人脸特征和虹膜特征权值设置相同,也就是权值取为θ1=θ2=0.5,作为加权算法的一个特例也参与评测。因此,本文是对以上9种算法给出评测结果。

表2给出了实验1中9种融合算法在样本特征泄露情况和正常情况下不同阈值的FMR、对应的容侵能力度量V及程序运行时间。

表2 实验1参数比较

在计算量方面,实验对比的9种算法原理各不相同,因此在计算量方面也相差较大。本文实验采用Matlab R2017b,计算机处理器Intel(R) Core(TM) i7-7700HQ CPU@2.80GHz 2.81GHz,内存8GB。由于串联、加法和加权3种方法融合之后不再对融合特征添加分类器,因此在9种算法中时间最短。其中,加法和加权两种融合算法得到的特征相比串联特征的维数更小,因此时间上最短。CCA算法比较特殊,与加权、复数融合方式不同,并不对两种模态特征直接做操作,算法执行的过程就是融合和分类的过程,因此时间也较短。而其他算法中,CKPCA和CKFDA两种算法在进行核函数计算生成核矩阵的过程中需要样本间两两遍历所有组合,大维数核矩阵的求解花费时间也长,造成两种算法时间较长,尤其CKFDA是CKPCA的基础上又进行了FDA,因此时间最长。CFDA、CCV和CLPP运行时间处于中间。

图3给出了实验1中9种融合算法在2种情况下FMR随阈值大小变化而变化的对比情况。随着阈值的增大,FMR也随之增大,这是因为样本类间距离小于阈值可能性就增加了,进而样本类间距离中小于阈值的个数将会增大,必然会使得FMR增大。然而,正常情况和泄露情况FMR增长的速率并不相同。从表2具体数值可看出,相同阈值下,串联、加法、加权、CFDA算法、CKPCA算法5种算法正常情况和泄漏情况FMR数值相似,进一步可看出相同阈值差值得到的FMR差值也是相似的,这也验证了图3中4种算法对应FMR增长曲线的相似性,从而表2给出的容侵能力度量V也是非常接近的。CCV算法和CCA算法正常情况下FMR增长速度相比泄露情况下FMR的增长速度过快,导致2种情况FMR相差较大,从而得到的容侵能力度量V也较大。从图3不难看出CKFDA算法和CLPP算法相对于其他7种算法在正常情况下和泄露情况下2条FMR曲线非常接近,尤其CLPP算法趋近于理想状况。CKFDA算法继承了实数域KFDA算法的优势,在增大类间距离的同时缩小类内距离,利用核函数将低维空间线性不可分问题转化为高维空间线性可分问题,提取更具有区分性的样本非线性特征。而CLPP算法更关注局部特征,保证在高维流形中相邻的样本在降维后的空间中也相邻,克服了线性算法不能保留高维数据中流形结构的缺点,充分利用同类间的非线性结构,在抵抗伪造特征攻击的表现更佳。从表2可以更方便地看出CLPP算法容侵能力度量最低。因此,从实验1的实验结果来看,如果从安全角度考虑融合算法,CLPP算法是较好的选择。

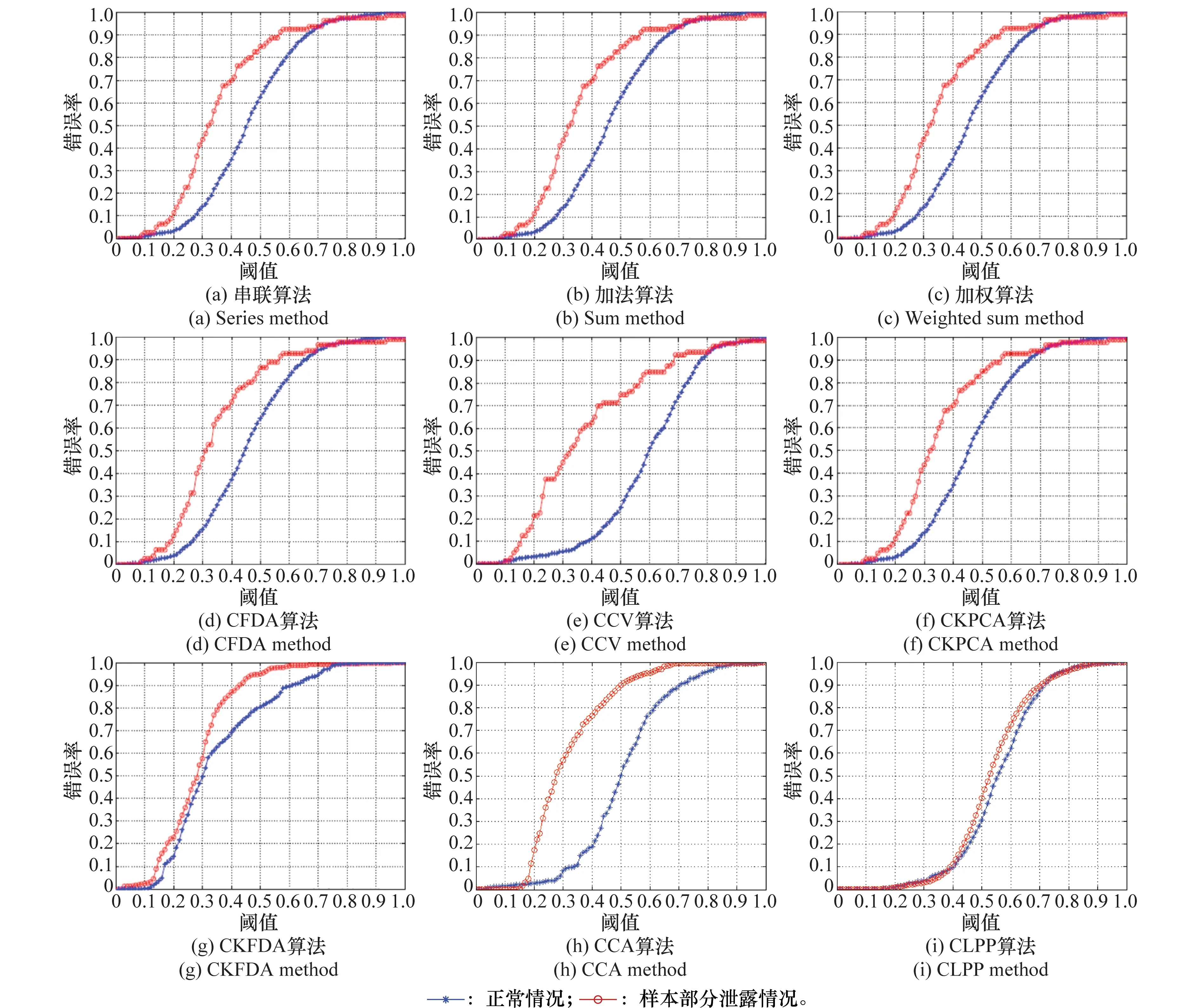
图3 实验1算法容侵能力比较Fig.3 Intrusion tolerance capability comparison of experiment 1

表3给出了实验2中9种融合算法在样本特征泄露情况和正常情况下不同阈值的FMR,对应的容侵能力度量V以及程序运行时间。计算机配置与实验1相同,9种算法程序运行时间差异与实验1也基本相同,但因为Yale库的样本数比ORL库样本少,因此表3中各算法运行时间都比表2中运行时间少。

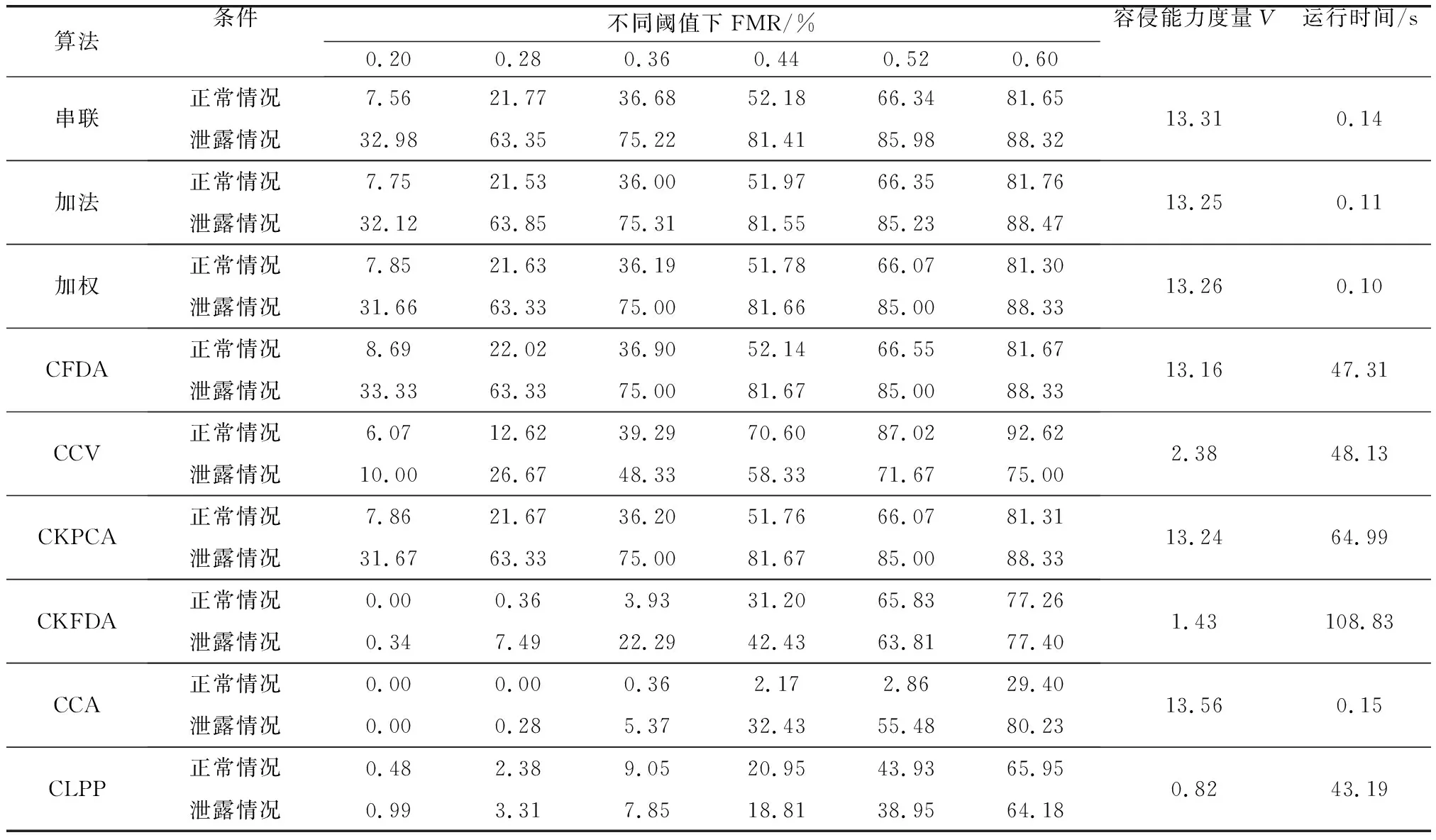
表3 实验2参数比较

图4给出了实验2中9种融合算法在2种情况下FMR随阈值大小变化而变化的对比情况。从表3和图4的实验结果,可看到实验2和实验1有相同的结论。相同阈值下,串联、加法、加权、CFDA算法、CKPCA算法5种算法正常情况和泄漏情况FMR数值相似,得到的容侵能力度量也是相近的。CCV算法和CCA算法在实验2中正常情况下FMR增长速度相比泄露情况下FMR的增长速度同样过快,导致2种情况FMR相差较大,从而得到的容侵能力度量V也较大。相比实验1,图4中CKFDA算法和CLPP算法在正常情况下和泄露情况下两条FMR曲线更加接近,尤其CLPP算法两条曲线几乎重合。因此,从实验1和实验2的实验结果来看,如果从安全角度考虑融合算法,CLPP算法是较好的选择。

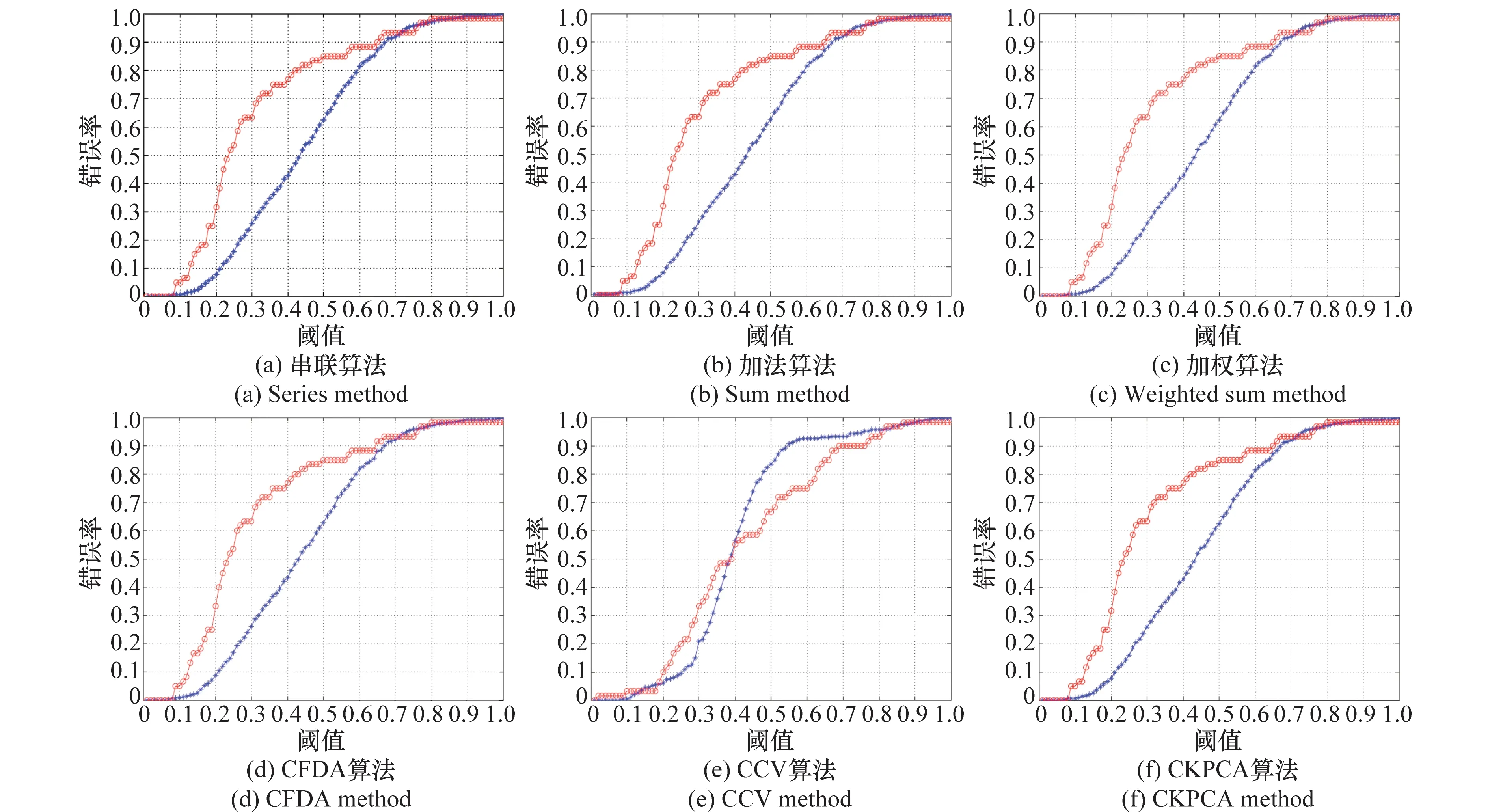
图4 实验2算法容侵能力比较Fig.4 Intrusion tolerance capability comparison of experiment 2

4 结 论

本文探讨了特征层多模态生物识别算法的安全问题,针对多特征中部分特征被窃取情况,引入入侵容忍概念,定义了安全威胁参数和容侵能力度量,提出了容侵能力评测方案,以人脸和虹膜为研究对象,对串联算法、加权算法、加法算法、CFDA算法、CCV算法、CKPCA算法、CKFDA算法、CCA算法和CLPP算法9种特征层双模态生物识别算法进行了评测。两组实验结果都表明CCV算法和CCA对于样本泄露造成的影响比较敏感,而CKFDA算法和CLPP算法对于样本特征被窃取情况的鲁棒性更高,保持了较高的安全性。