ZL108铸造铝合金拉压疲劳寿命曲线模型的建立与应用
2018-07-27,,,
,,,
(北京工业职业技术学院, 北京 100042)
0 引 言
疲劳破坏是工程结构和机械设备失效的主要原因之一。由于受到材料性能、载荷等因素的影响,疲劳寿命通常具有较大的随机性[1-2]。相对合金钢而言,铸造铝合金疲劳寿命的分散性更大,因此有必要对其进行统计分析。从可靠性角度建立疲劳寿命的概率模型,得出指定存活率下的疲劳寿命曲线,为结构寿命、可靠性评估提供模型基础[3]。疲劳寿命曲线常以应力幅S与寿命N之间关系的S-N曲线来描述,S-N曲线模型主要有指数函数、幂函数、Basquin公式、Weibull公式、多线性等[4],其中应用较多的是指数函数和幂函数。目前,国内外学者已对不同模型进行了研究、应用与比较[5-7]。在疲劳可靠性分析中,通常将S-N曲线参数作为随机量[3, 8],但部分S-N曲线参数仅仅是一个拟合数据,不具有实际的物理意义。
ZL108铸造铝合金是一种常用的铝合金,主要适用于制造汽车、拖拉机活塞和其他在250 ℃以下高温中工作的零件[9]。目前,有关ZL108铸造铝合金的研究主要集中在组织、力学性能、切削性能等方面,而对其疲劳性能的研究较少。因此,作者通过拉压疲劳试验,依据三参数幂函数建立了ZL108铸造铝合金的存活率-应力幅-寿命(P-S-N)曲线,利用疲劳试验中疲劳寿命统计数据得到结构疲劳失效极限状态函数,用于进行结构疲劳可靠性分析,并进行了试验验证。
1 试样制备与试验方法
试验材料为ZL108铸造铝合金,由金属熔融铸造法制备得到,抗拉强度为251~282 MPa,其化学成分(质量分数/%)为11.0~13.0Si,1.0~2.0Cu,0.4~1.0Mg,0.3~0.9Mn,余Al。按照GB/T 3075-2008,在ZL108铸造铝合金上截取如图1所示的试样,在加工过程中试样不能产生过热和冷作硬化,同时试样表面不可有划痕、损伤和腐蚀痕迹等;采用QBG-100型高频疲劳试验机进行轴向拉压疲劳试验,试验过程采用应力控制的对称拉压循环加载方式,加载频率为80 Hz,加载波形为三角波,试验环境为常温;考虑到铝合金材料一般无固定的疲劳极限,只开展循环次数在107周次以下的疲劳试验,加载应力幅分别为119,112,104,96,88,119 MPa应力下的试样数量为12个,其他应力下的均为15个。
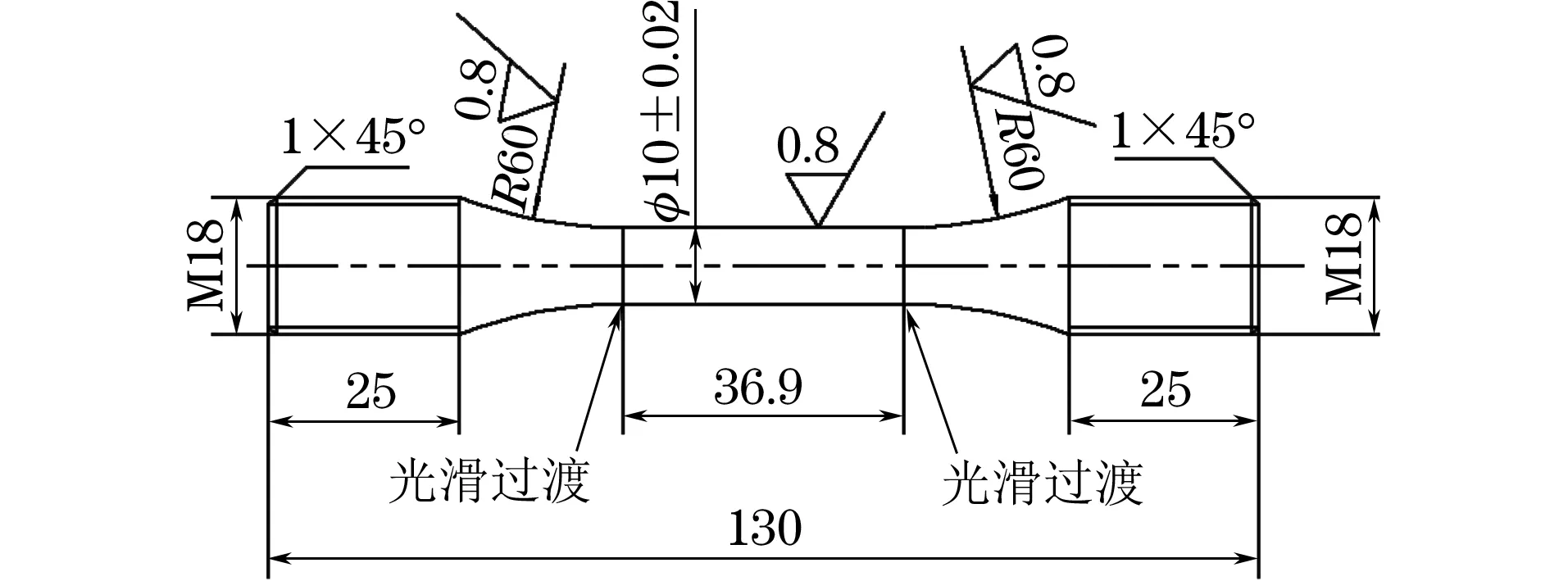
图1 试样的形状与尺寸Fig.1 Shape and size of specimen
2 试验结果与讨论
2.1 S-N曲线
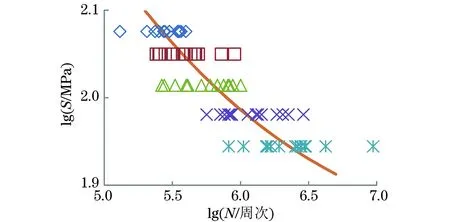
图2 ZL108铸造铝合金的S-N曲线Fig.2 S-N curve of ZL108 cast aluminum alloy
由图2可知,ZL108铸造铝合金的疲劳寿命随应力幅的增大而减小,且在每一应力水平下,疲劳寿命均具有较大的分散性。
2.2 疲劳寿命分布统计
计算得到不同应力下对数疲劳寿命的均值和标准差,如表1所示。经检验,不同应力下的对数疲劳寿命均服从正态分布,且对数疲劳寿命的变异系数在0.02~0.04范围内。

表1 ZL108铸造铝合金对数疲劳寿命的分布参数Tab.1 Distribution parameters of logarithmic fatigue life ofZL108 cast aluminum alloy
2.3 P-S-N曲线
用工程上常用的三参数幂函数拟合ZL108铸造铝合金的S-N和P-S-N曲线。S-N曲线拟合函数表达式为
S=C(1+A/Nα)
(1)
式中:C为N→∞时对应的S,即理论中值疲劳极限;A,α均为S-N曲线参数。
P-S-N曲线拟合函数表达式为
S=CP(1+A/NαP)
(2)
式中:CP为指定P下的理论安全疲劳极限,由最大相关系数法确定;αP为P-S-N曲线参数。
对式(2)两边取对数,得
lg(S/CP-1)=lgA-αPlgN
(3)
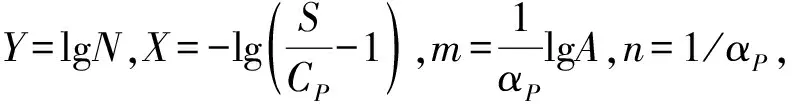
Y=nX+m
(4)
基于疲劳试验数据,利用最小二乘法拟合双对数疲劳寿命曲线,从而确定不同存活率下的曲线参数,如表2所示,从而得到ZL108铸造铝合金在不同存活率下的S-N曲线,即P-S-N曲线,如图3所示。
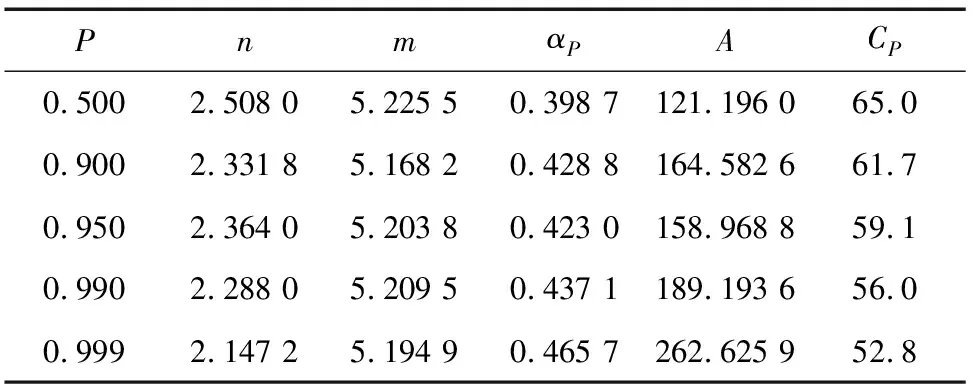
表2 ZL108铸造铝合金P-S-N曲线的拟合参数Tab.2 Fitting parameters of P-S-N curves of ZL108cast aluminum alloy
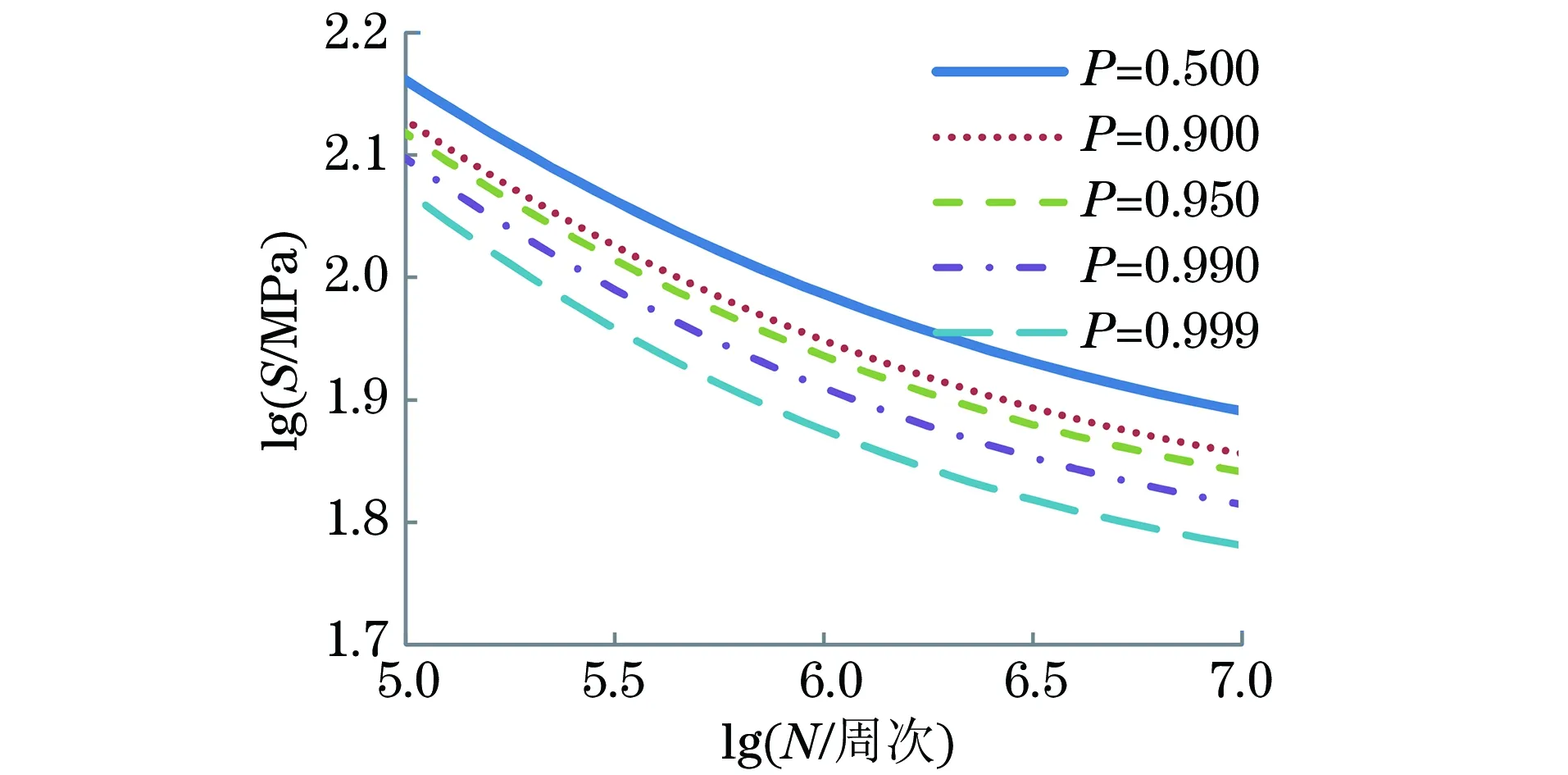
图3 ZL108铸造铝合金的P-S-N曲线Fig.3 P-S-N curves of ZL108 cast aluminum alloy
由图3可知,在同等应力水平下,存活率越大,疲劳寿命越短。图3为ZL108铸造铝合金标准试样的P-S-N曲线,在应用于结构疲劳设计之前,应考虑结构的应力集中、尺寸、表面质量等因素影响,对其应力或P-S-N曲线参数进行修正[3]。
3 P-S-N曲线模型的应用与分析
3.1 结构疲劳寿命计算
若已知结构所承受的应力幅Ss,考虑疲劳因素可折算为材料的等效应力幅S。由式(3)和表2的数据,可计算得到可靠度为0.500,0.900,0.950,0.990,0.999下的结构疲劳寿命,即
(5)
若结构承受的载荷谱为非恒幅应力谱,则可利用Miner准则中的等累积损伤方法[4]进行损伤累积,然后计算其疲劳寿命。
3.2 结构疲劳可靠性分析
若结构的实际寿命低于其设计寿命Ng时,则认为该结构失效,即该结构不可靠。根据结构可靠性理论,结构疲劳失效的极限状态函数[4]为
Z=N-Ng
(6)
式中:Z为结构极限状态值。
当Z>0时表示结构可靠,满足设计要求;当Z<0时表示结构失效,不满足设计要求;当Z=0时结构为临界状态。
由式(5)可知,结构的实际寿命与结构应力、材料的S-N曲线参数、疲劳修正系数有关,而结构应力与外加载荷、结构尺寸、弹性模量、应力集中等有关。因此,结构疲劳寿命是材料S-N曲线参数、结构尺寸、载荷等参数的函数。在实际工程中,大部分的材料S-N曲线参数、结构尺寸、载荷等均为随机变量,其大小服从一定的随机分布。确定各参数的随机分布及其参数后,利用一次二阶矩、蒙特卡洛等方法,通过式(6)得到结构疲劳失效概率或结构可靠度。但是,在疲劳可靠度计算中,S-N曲线参数A,α没有具体的物理意义,其随机分布的参数也较难获取,因此利用疲劳试验中的疲劳寿命统计数据替代S-N曲线参数,建立ZL108铸造铝合金结构的疲劳失效极限状态函数来进行疲劳可靠性分析。
由于P-S-N曲线中的长寿命段在双对数坐标系中是一条直线,而且由表1可知,不同应力水平下的对数疲劳寿命均值均分布在P=0.500的S-N曲线附近,如图4所示。
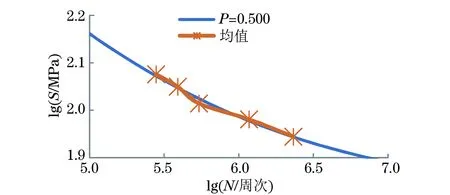
图4 ZL108铸造铝合金的疲劳寿命均值与P为0.5时的S-N曲线Fig.4 Mean value of fatigue life and S-N curve at P of 0.5 of ZL108 cast aluminum alloy
令应力水平119.069 4,112.178 5,103.358 6,95.687 8,88.007 8 MPa分别为S1,S2,S3,S4,S5,则对应的对数疲劳寿命分别为L1,L2,L3,L4,L5,则疲劳寿命近似表示为
(7)
式(7)中L1,L2,L3,L4,L5一般服从正态分布,其分布参数由疲劳试验数据即可获取。将式(7)代入式(6)建立结构疲劳失效的极限状态函数,利用一次二阶矩、蒙特卡洛等方法[3]求解结构疲劳可靠度。
4 试验验证
试验材料为带中心孔的ZL108铸造铝合金板,尺寸如图5所示,宽度W为50 mm,孔直径D为8 mm。对铝合金板两端施加均匀分布的对称循环拉压应力,最大应力为40 MPa,对其疲劳寿命进行分析。

图5 带中心孔ZL108铸造铝合金板的尺寸Fig.5 Size of ZL108 cast aluminum alloy sheet with a center hole
由D/W=0.16,查机械设计手册[10]得应力集中系数K为2.6,尺寸系数ε取0.95。不考虑表面粗糙度的影响,则修正应力水平为109.47 MPa。利用式(5)和表2中的数据,分别计算可靠度为0.500,0.900,0.950,0.990,0.999时的疲劳寿命,结果如表3所示。
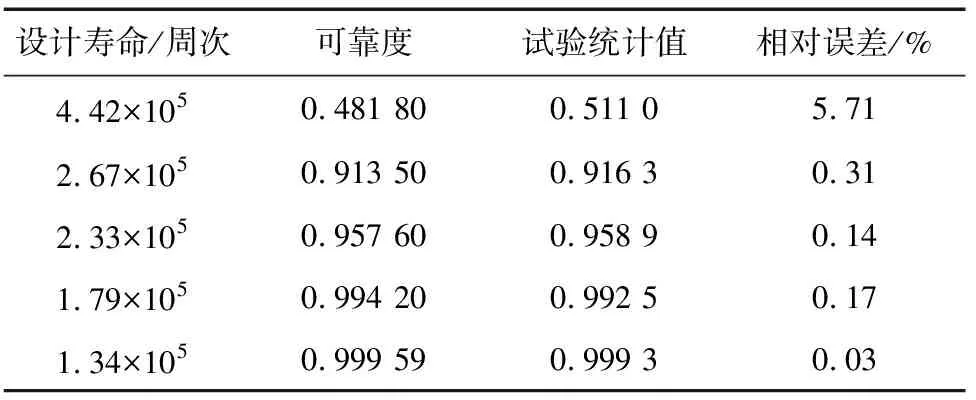
由于S2<109.47 (8) 为验证疲劳可靠性分析方法,只考虑L2和L3的随机性,利用一次二阶矩方法分别求出疲劳寿命为4.42×105,2.67×105,2.33×105,1.79×105,1.34×105时的结构可靠度,计算结果如表4所示。 表3 计算得到带中心孔ZL108铝合金板的疲劳寿命Tab.3 Calculated fatigue live of ZL108 cast aluminum alloysheet with a center hole 表4带中心孔ZL108铸造铝合金板的结构可靠度与试验统计值的对比 Tab.4ComparisonofstructurereliabilitydegreeandexperimentalstatisticofZL108castaluminumalloysheetwithacenterhole 设计寿命/周次可靠度试验统计值相对误差/%4.42×1050.481 800.511 05.712.67×1050.913 500.916 30.312.33×1050.957 600.958 90.141.79×1050.994 200.992 50.171.34×1050.999 590.999 30.03 取10个如图5所示的带中心孔的ZL108铸造铝合金板试样,在QBG-100型高频疲劳试验机上进行疲劳试验,采用最大应力为40 MPa的拉压循环载荷。由试验结果可知,各试样的疲劳寿命分别为203 147,366 049,334 598,428 952,423 306,597 500,691 854,460 403,854 757,486 208周次,其对数疲劳寿命均值为5.65,标准差为0.165。经检验,该铝合金板的对数疲劳寿命服从正态分布。由设计疲劳寿命即累积分布值确定对应的概率,即为试验统计值,之后计算可靠度相对于试验统计值的误差,结果列于表4中。由表4可以看出,通过疲劳可靠性分析方法,利用疲劳试验数据计算得到的可靠度与试验结果比较吻合,最大相对误差为5.71%。因此,可以直接利用疲劳试验数据进行疲劳可靠性分析,解决S-N曲线参数A,α存在随机性而难以获取的问题。 (1) ZL108铸造铝合金的疲劳寿命随应力的增大而减小,且在每一应力水平下,疲劳寿命具有较大的分散性;根据ZL108铸造铝合金的疲劳试验数据,确定不同应力水平下的对数疲劳寿命均服从正态分布,得到了ZL108铸造铝合金的P-S-N曲线。 (2) 通过建立的ZL108铸造铝合金结构的疲劳失效极限状态函数计算得到的可靠度与试验结果比较吻合,最大相对误差为5.71%。
5 结 论
