粉末热等静压制备Ti6Al4V合金在α+β两相区的热压缩行为
2018-07-27,,,,,
,,, ,,
(1.华中科技大学,材料成形与模具技术国家重点实验室,武汉 430070;2.中国航发北京航空材料研究院铸钛技术中心,北京 100089)
0 引 言
Ti6Al4V合金具有密度小、比强度高、耐腐蚀性能好等特点,已广泛应用于航空、航天、舰船等方面。随着制造技术的不断进步,材料成形技术逐步向高性能、整体化成形、快速成形和无余量近净成形的方向发展[1]。铸造方法能够实现复杂构件近净成形,但铸造钛合金存在组织粗大、成分偏析、缩孔和疏松缺陷等问题,导致其塑性差,使用可靠性低,只能用于一些非关键结构部件[2];锻造钛合金的力学性能突出,但难以直接成形出复杂结构件,而且锻造钛合金的机械加工性能差、材料成本高:因此催生了钛合金近净成形技术的发展。粉末冶金结合热等静压技术作为一种新兴的近净成形方法,其材料利用率高,制备的合金组织均匀细小、力学性能与锻造合金的相当,因此该成形技术受到越来越多的关注[3]。
在粉末热等静压过程的高温高压作用下,粉末的致密化过程涉及颗粒的平移、翻转以及塑性变形等一系列复杂变化,同时粉末热等静压是一个涉及到大压缩复杂变形的热加工过程,而且热等静压炉的密闭性导致对粉末热等静压过程进行实时动态研究的难度较大,但是这些问题均可以通过数值模拟来解决。数值模拟不但可以节约研究成本,而且还可实时动态再现热等静压过程中粉末的致密化过程,并可对不同热等静压工艺下粉末的致密性、应力应变、包套变形情况等多种物理量的变化过程进行预测,从而为研究粉末热等静压过程提供参考。近年来,随着计算机技术的发展,基于有限元的商业软件如Abaqus,Ansys,MSC.Marc等在金属热加工的研究中得到越来越广泛的应用,而建立准确的流变应力模型是提高数值模拟精度的关键。
目前,许多学者通过热压缩试验获得了不同热加工条件下不同材料的应力-应变曲线,并基于Arrhenius方程得到了不同合金在热变形下的本构方程[4-6],同时还有通过Fields-Backofen模型[7]、Johnson-Cook模型[8]来研究材料热压缩过程的流变应力本构方程,但是现有研究很少涉及到粉末热等静压领域。在粉末热等静压制备Ti6Al4V合金时,温度基本控制在该合金熔点的50%~70%,而在该温度范围内Ti6Al4V合金为典型的α+β两相组织,因此作者通过对粉末热等静压制备的Ti6Al4V合金进行高温压缩试验,建立了可描述合金在两相区压缩行为的本构方程,对合金热加工过程中的加工硬化、动态软化参数和动态再结晶动力学模型进行求解,并构建了合金在两相区的流变应力模型,为钛合金粉末热等静压过程的数值模拟提供依据。
1 试样制备与试验方法
试验原料为由宝鸡海宝特种金属材料公司提供的采用等离子旋转电极工艺生产的Ti6Al4V合金粉,粒径为40~200 μm,化学成分如表1所示,形貌如图1所示。由图1可知,Ti6Al4V合金粉颗粒呈球形,少量颗粒带有行星球,表面光滑,未见孔洞。
采用QIH215型热等静压机对Ti6Al4V合金粉进行包套热等静压,温度为1 000 ℃,压力为120 MPa,时间为3 h,圆柱形包套的壁厚为3 mm,内径为24 mm,高度为90 mm。制备得到的Ti6Al4V合金用由3 mL HF、6 mL HNO3和100 mL水组成的Kroll腐蚀剂腐蚀后,采用Mzto MR6000型光学显微镜观察其显微组织。
采用阿基米德排水法测合金的相对密度,在相对密度95%以上的合金上截取热压缩试样,尺寸为φ6 mm×9 mm,采用Gleeble3500型热模拟试验机进行高温热压缩试验,变形温度在645~720 ℃,应变速率分别为0.1,1.0,10.0 s-1,最大应变为0.8。在试验过程中,先将试样以2 ℃·s-1的速率加热到1 200 ℃,保温3~5 min,然后以2 ℃·s-1的冷却速率降至变形温度,保温1 min,然后以不同的应变速率对试样进行热压缩,变形完毕后立即水淬。
2 试验结果与讨论
2.1 显微组织
由图2可以看出:试验合金的组织主要由等轴α相、层片状α相和相间β相组成,层片状α相宽6~10 μm,长10~30 μm,β相宽约1 μm,分布在α相边界处;合金组织呈典型的网格结构,每个网格的大小与热等静压前粉末颗粒的尺寸接近,网格的内部由相互交错的层片状α相组成,网格与网格之间由一圈圈细小的等轴α相区分。在热等静压过程中,颗粒在发生塑性变形前已相互接触或相互楔住,只有颗粒边界局部区域发生大的塑性应变与晶格畸变,形成边界大应变带;由于边界大应变带中积累了较大的应变能,在保温保压过程中,边界大应变带发生了动态回复与再结晶,形成大量等轴α相,这些等轴α相在原始颗粒边界处聚集,形成空间网状结构。

图2 试验合金的显微组织Fig.2 Microstructure of tested alloy: (a) at low magnification and (b) at high magnification
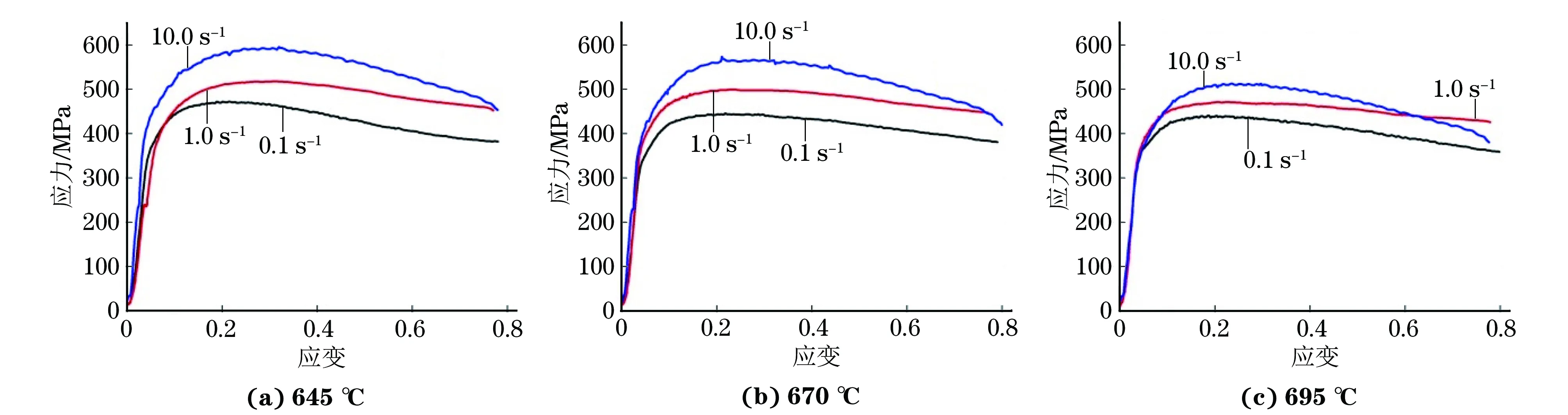
图3 试验合金在不同温度和不同应变速率下高温压缩变形的应力-应变曲线Fig.3 Stress-strain curves of tested alloy during hot compression deformation at different temperatures and strain rates
2.2 高温压缩变形的应力-应变曲线
由图3可知:不同温度下,试验合金在变形初始阶段的流变应力均随应变的增加而急剧增大,这是由合金变形所产生的加工硬化所导致的;随着应变的增加,位错通过攀移和交滑移使合金发生动态回复,导致流变应力的增大速率下降;不同温度、不同应变速率下的应力-应变曲线都存在一个峰值,达到峰值应力后应力开始下降,这是因为当应变积累到一定程度后,合金发生了动态再结晶,由动态再结晶产生的软化作用占主导,从而导致位错密度降低,流变应力减小;当达到一定的应变后,流变应力基本不变,这是由于此时加工硬化与软化作用相互抵消,使得流变应力稳定;当变形温度相同时,相同应变下的流变应力随应变速率的增加而增大,且应变速率越大,峰值应力出现的越晚,这是因为应变速率越大,合金动态回复和再结晶等软化过程进行的时间越短,软化作用越弱,从而导致流变应力增大;当应变速率相同时,相同应变下流变应力随变形温度的升高而变小,这是因为变形温度越高,合金的热激活作用越强,原子的扩散速率越大,变形过程中有更多的位错产生攀移和交滑移,动态回复的软化作用越强,从而导致流变应力减小,同时再结晶过程是通过形核和长大来进行的,温度越高,越有利于形核,由动态再结晶导致的软化作用增强,从而使得流变应力减小。
2.3 两相区热压缩变形本构方程的建立
在热变形过程中,流变应力与应变、应变速率和变形温度相关。SELLARS等[9]通过研究不同金属材料在塑性变形过程中的数据,推导出了涵盖热激活能和温度的本构方程,即Arrhenius方程,表达式为
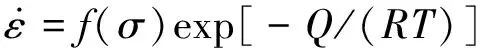
(1)

流变应力具有幂指数、指数和双曲正弦3种形式[10-11],表达式为
(2)

在热变形过程中,应变速率受到热激活能的控制,变形温度和应变速率对变形的影响通过引入参数Z[12]来表示,表达式为
(3)
SELLARS等[13]认为金属在高温塑性变形时,可用双曲正弦函数来描述流变应力、应变速率和变形温度之间的关系,其表达式为
(4)
式中:A,n均为与材料相关的常数。
通过联立式(1)~式(4)可以得到流变应力的本构模型,即
(5)
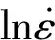
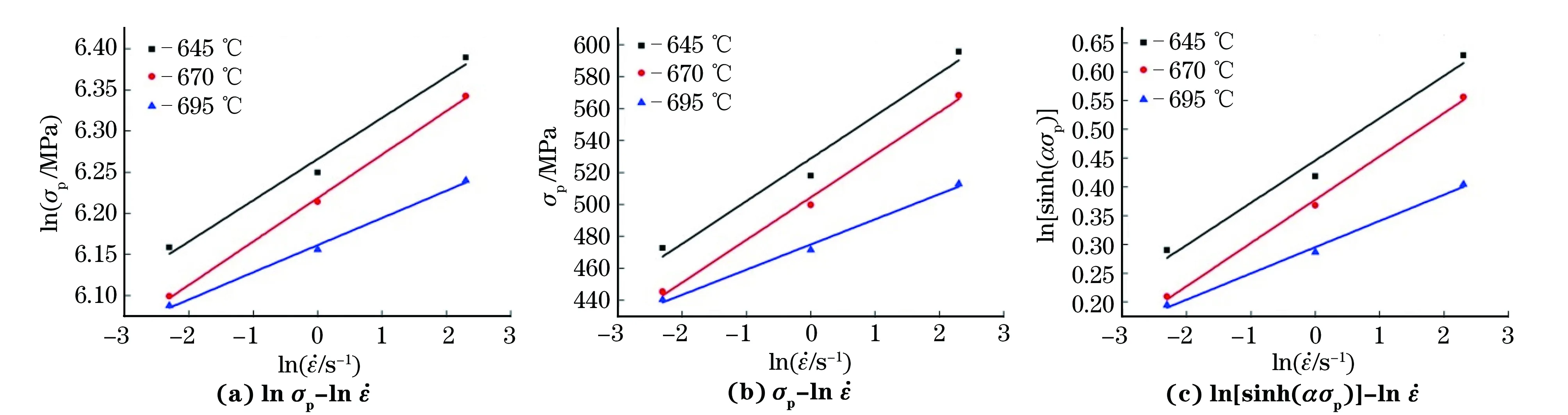
图4 试验合金的峰值应力与应变速率对数的拟合曲线Fig.4 Fitting curves of peak stress vs strain rate logarithm of tested alloy

图5 试验合金的ln[sinh(ασp)]-T-1以及lnZ-ln[sinh(ασp)]拟合曲线Fig.5 Fitting curves of ln[sinh(ασp)] vs T-1 and lnZ vs ln[sinh(ασp)] of tested alloy
假定热变形过程中的热激活能在一定温度范围内与温度无关,对式(2)中双曲正弦表达式取对数求偏微分,可得热激活能的计算公式为
(6)
根据试验数据作出ln[sinh(ασp)]-T-1的拟合曲线,如图5(a)所示;对式(4)两边取对数,根据试验数据对lnZ与ln[sinh(ασ)]的关系进行线性拟合,结果见图5(b),所得直线的截距即为A。相关参数的数值模拟结果如表2所示。

表2 相关参数的数值拟合结果Tab.2 Numerical fitting results of related parameters
联立式(3)和式(4)可以得到
Z=A[sinh(ασ)]n
(7)
将表2中的参数代入式(7),得到粉末热等静压所得Ti6Al4V合金在两相区热压缩变形的本构方程为
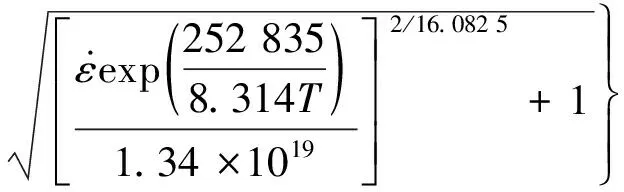
(8)
2.4 两相区流变应力模型的建立
2.4.1 应力-应变曲线特征点的确定
具有明显动态再结晶特征的材料的流变应力-应变曲线上的特征点主要有临界应力、峰值应力、稳态应力和饱和应力。材料发生动态再结晶时的应变为临界应变,而临界应变所对应的流变应力为临界应力;材料发生动态再结晶后,软化作用增强,但在一定范围内流变应力仍继续增加,当应变达到峰值应变后,加工硬化与软化作用达到平衡,此点的应力为峰值应力;当应变超过峰值应变后,软化作用占主导地位,流变应力开始下降,直到应变达到稳态应变,此时加工硬化与软化作用再次达到平衡,之后的流变应力不再随应变而变化,此点的应力称为稳态应力;若材料再无动态再结晶发生,由变形引起的加工硬化和动态回复引起的软化作用最终达到平衡,流变应力达到稳态,此时的稳态应力称为饱和应力。高温应力-应变曲线是材料在热变形过程中微观变化及组织演变的宏观表征,而组织演变过程中的临界点亦可通过应力-应变曲线上的特征点进行捕捉。根据加工硬化理论,在热变形过程中,流变应力在达到峰值前,加工硬化率θ随应力的变化大致分为易滑移阶段、线性硬化阶段、动态回复阶段、大应变硬化阶段以及动态结晶软化阶段。其中,动态回复阶段和大应变硬化阶段分别对应着流变应力-应变曲线上的临界点,NAJAFIZADEH等[14]简化了Poliak-Jonas模型[15-16],考虑用三阶多项式拟合θ-σ曲线,从而确定动态再结晶的临界应力及临界应变。作者根据NAJAFIZADEH等[14]和POLIAK等[15-16]提出的模型,用数学方法对粉末热等静压制备的Ti6Al4V合金的应力-应变曲线进行处理,确定热压缩时的临界条件。取θ-σ曲线的动态回复阶段和大应变硬化阶段的试验数据,通过三次多项式拟合得到θ和σ的关系,其拟合公式为
θ=E1σ3+B1σ2+C1σ+D1
(9)
式中:E1,B1,C1,D1均为三次多项式的系数,具体数值由拟合结果决定。
根据加工硬化率理论,大应变硬化阶段和动态回复阶段之间存在一个拐点,该拐点即为发生动态再结晶的临界条件,对式(9)求导即可得到发生动态再结晶的临界应力σc表达式为
σc=-B1/(3E1)
(10)
对不同温度和应变速率下Ti6Al4V合金θ-σ曲线中大应变硬化阶段和动态回复阶段的数据进行拟合,结果见图6。
发生动态再结晶的临界应变εc也是重要的临界条件,对加工硬化率和应力作如下变换:
(11)
由式(11)可知,θ-σ曲线与lnθ-ε曲线的拐点为同一拐点。
对lnθ-ε曲线上的大应变硬化阶段、动态回复阶段的试验数据进行三次多项式拟合,得到发生动态再结晶的临界条件为
(12)
对不同温度和应变速率下试验合金加工硬化率-真应变中大应变硬化阶段和动态回复阶段的试验数据进行拟合,结果见图7。
基于上述计算方法,根据热压缩试验得到的流变应力-应变曲线,通过引入参数Z,拟合得到峰值应变εp、临界应力σc、临界应变εc、饱和应力σs、稳态应力σss与热变形参数之间的关系为
σc=115.433Z0.041 57
(13)
εp=0.022 195Z0.073 8
(14)
εc=0.58εp
(15)
σs=429.553 3sinh-1(0.144 923Z0.072 7)
(16)
σss=429.553 3sinh-1(0.307 955Z0.040 09)
(17)
由流变应力-应变曲线可以看出,在热压缩过程中,弹性部分表现不明显,对该阶段的试验数据进行拟合得到起始应力σ0,表达式为
σ0=0.579 28Z0.104 25
(18)
2.4.2 加工硬化动态软化参数的求解
位错密度在金属热塑性变形过程中起着重要的作用,再结晶晶粒的形核、长大速率及其停止生长的时间等都与位错密度息息相关。在热变形过程中,加工硬化与动态软化总是同步进行的,位错密度的变化取决于这两个过程竞争的结果。针对热变形过程中位错密度随应变的增加而不断增长的现象,MECKING等[17]基于塑性流动动力由位错密度变量来决定的假设,提出了KM唯象模型,表达式为
(19)
k1=2θ0/(αμb)
(20)
k2=2θ0/σs
(21)
式中:ρ为位错密度;k1为硬化系数,代表加工硬化对位错密度的影响;k2为软化系数,代表动态软化对位错密度的影响;θ0为初始的加工硬化率,θ0=dσ/dε;α为与位错密度相关的系数,一般取0.5;μ为剪切模量;b为博格斯矢量,取2.54×10-10。
对式(19)积分可以得到
(22)
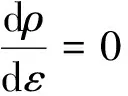
ρs=(k1/k2)2
(23)
式中:ρs为加工硬化过程外延饱和位错密度,其对应着饱和应力。
材料发生高温塑性变形所需的应力主要包括位错的增殖和位错间的阻力,流变应力和位错密度的关系可用Taylor公式进行描述,公式为
(24)
将式(23)代入式(22),并联立式(24)得到仅有动态回复时,瞬时应力σWH的表达式为
(25)
根据发生动态再结晶前的应力-应变曲线可以求出k2和k1,不同热变形条件下的k1,k2分别与参数Z进行拟合,拟合曲线如图8所示,拟合公式为
k1=7.298×109Z0.016 08
(26)
k2=143.449 1Z-0.037 86
(27)
2.4.3 动态再结晶动力学模型的建立
在热变形过程中,材料显微组织的演化对流变应力会产生非常大的影响。当应变大于临界应变时,材料将发生动态再结晶,而式(25)只是材料仅存在动态回复时的瞬时流变应力模型,当发生动态再结晶后,流变应力模型将发生改变,因此必须先确定动态再结晶动力学模型才能确定流变应力模型。为了建立动态再结晶动力学模型,需要根据流变应力-应变曲线计算出动态再结晶分数Xdrx,动态再结晶分数的计算公式为
(28)
由式(28)计算得到的不同热变形条件下的动态再结晶分数如图9所示。

图8 不同热变形条件下试验合金的ln Z与ln k1、ln k2的拟合曲线Fig.8 Fitting curves of lnZ vs ln k1 and ln Z vs ln k2 of tested alloy under different hot deformation conditions
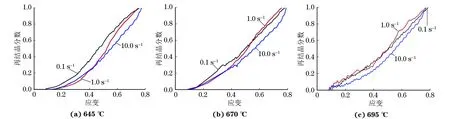
图9 不同热变形条件下试验合金的动态再结晶分数随应变的变化曲线Fig.9 Dynamic recrystallization fraction vs strain curves of tested alloy under different hot deformation conditions
SELLARS等[18]提出,动态再结晶动力学模型可以用式(29)来描述。
(29)
式中:kd和nd均为与材料相关的常数。
对ln[-ln(1-Xdrx)]和ln[(ε-εc)/εp]进行拟合,得到nd=1.889 583,kd=0.279 917。
联立式(28)和式(29),得到试验合金在两相区动态再结晶阶段的流变应力模型为
σ=σWH-
(ε>εc)
(30)
将试验合金在α+β两相区不同热变形条件下的流变应力计算结果与试验结果进行对比。由图10 可以看出,所建立的流变应力模型的计算结果与试验结果吻合得较好,流变应力模型具有较高的准确性。

图10 不同热变形条件下试验合金的流变应力计算结果与试验结果的对比Fig.10 Comparison of the flow stress between predicted results and experimental results of tested alloy under different deformation conditions
3 结 论
(1) 采用粉末热等静压技术制备的Ti6Al4V合金组织由α相和β组成,呈典型的网格结构,网格由细小的等轴α相形成,网格内部为相互交错的片层状α相,β相分布在α相边界处。
(2) 不同温度变形时,Ti6Al4V合金在变形初始阶段的流变应力均随应变的增加而急剧增加;随着应变的增加,流变应力的增大速率下降;当达到峰值应力后流变应力开始下降;当达到一定的应变后,流变应力基本不变。
(3) 根据Ti6Al4V合金在热压缩过程中的流变应力-应变曲线,通过线性回归的方法建立了适用于描述Ti6Al4V合金在α+β两相区热压缩行为的本构方程。
(4) 基于Ti6Al4V合金在热压缩过程中的流变应力-应变曲线,建立了表征合金热变形过程中临界特征点与热变形参数之间的数值关系,同时构建了热变形过程中加工硬化、动态软化以及动态再结晶动力学模型,并在此基础上建立了适用于Ti6Al4V合金α+β两相区的流变应力模型,该流变应力模型的计算结果与试验结果吻合较好,验证了流变应力模型的准确性。
