基于NSGA-II快递智能仓库多目标优化问题研究

2018-07-27，

现代机械 2018年3期

，

(广东工业大学机电工程学院，广东广州 510006)

0 引言

随着电子商务的兴起，智能仓储已经发展成为一个极具市场价值和发展前景的行业，智能仓库调度方案的好坏直接关系到整个仓储系统出入库和整个物流过程的效率。对于现在的大型智能仓库，一个订单往往对应多个物品，同时下单的多个物品往往通过同一快递物流分发到客户手中。本文就这一现象进行生产调度研究。

本文要研究的内容可以归结于混合流水车间调度问题。混合流水车间是一种复杂的组合问题。国内外的主要研究有两级作业混合流水车间。在这类问题中Ruiz[1]，Gupta[2]和Li[3]研究了两级作业混合流水车间，最大完工时间最优化的问题。Lin[4]研究了两级混合流水车间，且各个阶段引入了时间驱动的概念，对目标函数重新设置，最大限度地在原有的顺序上进行优化。Haouari[5]使用新的优化算法区去解决混合流水车间的问题，同时他给出了较为详细的解决步骤和方案。Allaoui[6]从机器故障等中断点的角度去优化混合流水车间，研究中引入了中断的解决方案。Logendran[9]引入群混合流水车间，优化最大完工时间。Botta-Genoulaz[10]研究了混合流水车间的步骤限制和时间滞后。Voss[11]介绍了从批处理的角度去解决混合流水车间问题，引入了重中的处理的目标机制。国内外的研究中，引入了众多新的解决方法。其中Engin[7]采用了人工免疫算法。Uiusoy[8]用基因算法来优化多级混合流水车间的多重处理任务调度问题。Zitzler[12]使用进化的Pareto对目标进行优化。Deb[13]使用NSGA的改进方法对目标函数进行优化。

在这些研究中很少提到带有集中打包的混合流水车间，本文从准时度和同时度两个层面，考虑到集中打包策略的混合流水车间多目标调度，并且通过对智能算法进行优化最后实现优化调度方案。

1 调度模型的建立

1.1 研究问题描述

本文研究的是一个考虑到集中打包的生产调度问题，在大型网站购物中客户的一个订单可能对应多个物品，每个物品都需要经过几道工序才能打包。每个物品到达打包区域的时间都不一样，例如：一个订单有3个物品，其中2个物品已经完成出库阶段，这2个物品就需要在缓冲区等待最后的一个物品才能进入打包环节，如果调度不合理，那么就有大量的物品在缓冲区等待打包，缓冲区库存过大将不利于仓库的管理。结合这一问题，本文提出了同时度和准时度两个目标优化指标。

如图1所示，是智能仓库一个订单对应多个快递物品从出库到打包的流程图。在本文中我们把智能仓库的工作生命周期分为两个过程：1)出库过程，这一过程就是物品的拣货、增加填充、运输等阶段的集合；2)打包过程，这一过程就是物品封装打包的过程，打包结束后就完成一个订单的在智能仓库中的生命周期，从而进入下一个物流环节。

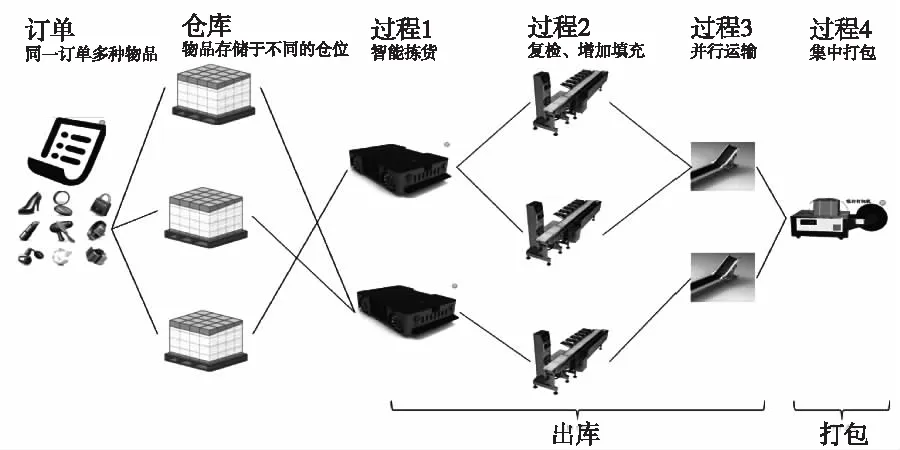
图1 智能仓库从出库到打包过程图

1.2 量化模型建立

通过对问题的研究，将现实的问题量化，将现实问题转换为数学问题，将整个过程量化为出库和打包两个过程。

1.2.1 同时度的定义和设定

对于智能仓库来说，一般情况下智能仓库的出库量巨大，对于一个订单中包含多个物品的情况，往往多个物品不是同时到达打包区。这里就存在一个问题，如果，多个物品等待一个物品才能打包，那么这多个物品将在Buffer区中等待，直至所有的物品都到达。如果这种情况过多，buffer区的库存物品就会很多，不利于整个智能仓库的管理，也不利于存放。所以基于这个考虑，我们的第一个目标函数就是同一个订单的多个物品到达打包区的同时度。目标函数式(1)是尽量让同一个订单内的多个物品能同时到达打包区域，从而尽量的减少buffer区域的库存物品。

f1(x)=minCT

=1，…，P；

(1)

1.2.2 准时度的定义和设定

对于每一个订单而言，都会有一个规定的发货日期，智能仓库必须保证，在预定的发货期到来前所有的来自于同一个订单的物品能够到达打包区域。目标函数式(2)就是要让所有的物品都尽量的在预定的发货前能够到达指定的打包区域，而不存在推迟发货等情况。

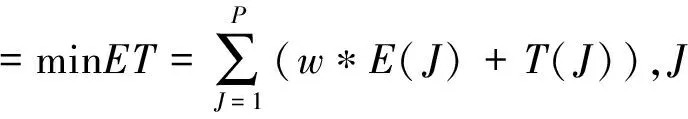
=1，…，P；

(2)

上面的(1)和(2)式就构成了本模型的目标函数，(1)表达的是同一个订单的多个物品同时到达打包区域的时间间隔最小，(2)则表示的是每个订单的打包完成后的发货时间与预计的发货时间间隔最小。

2 基于优化的NSGA-II模型的建立

NSGA-Ⅱ算法是 Srinivas和Deb 于 2000 年在 NSGA 的基础上提出的，它比 NSGA算法更加优越：它采用了快速非支配排序算法，计算复杂度比 NSGA低很多；采用了拥挤度和拥挤度比较算子，代替了需要指定的共享半径 shareQ，并在快速排序后的同级比较中作为胜出标准，使准 Pareto 域中的个体能扩展到整个 Pareto 域，并均匀分布，保持了种群的多样性；引入了精英策略，扩大了采样空间，防止最佳个体的丢失，提高了算法的运算速度和鲁棒性。

本文采用改进的NSGA-Ⅱ算法。改进的NSGA-II具体采用的流程如图2 所示，本文较之前的NSGA-II算法，对父代生成新个体，增加精英选择机制，在以往的流程中往往存在一些交叉的信息，在改进的流程中将增加优化策略，将重复的迭代个体进行精英刷选。经过优化的NSGA-II模型的种群类型更加合理，不存在大量重复的冗余个体。

图2 改进的NSGA-II流程图

算法改进的具体过程为：种群个数为N，带精英策略的NSGA-Ⅱ算法将父代与子代个体合并，合并后的种群个数大于N，比较个体中的目标函数值，相同个体只保留一个，由于是带精英策略，保证了改进之后得到的新种群中的个体数大于等于N，再从里面按规则选取优良的N个个体成为下一代父种群。

图3 改进前后的NSGA-Ⅱ算法结果比较

对改进后的带精英策略的NSGA-Ⅱ进行上述实验，算法得到的Pareto解图如图3。

如图3，图中的“+”点是改进后算法得到的终止迭代种群中的Pareto解，“⊕”点是带精英策略NSGA-Ⅱ算法得到的解。

从图3可以看出：优化后的点组成的解集数多于优化前的解集数，且对于目标函数的结果优于之前，所以本优化的NSGA-II作用较好。

3 仿真实验及稳定性分析

3.1 仿真实验

基于上面几节研究的方法，在MATLAB上进行编码实验。如表1，通过MATLAB生成相应的数据，用于实验。

表1 参数生成

在生成实验数据后，我们的实验将对NSGA-II算法的重要指标进行设置。在算法中主要涉及到的参数有：种群大小POP，交叉概率Pc，变异概率Pm，进化代数Gen。这四个因子的取值如表2，仿真结果、甘特图集Pareto解集的生成如图4、图5。

表2 NSGA-II参数设定

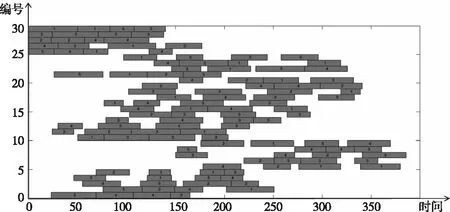
图4 调度甘特图

图4是基于模拟的数据，通过NSGA-II求解的一种最优的调度方案。图5为多目标优化问题中的两个目标的Pareto解集。

图5 多目标优化的Pareto解集

多目标优化，通过算法得到了一组较优的Pareto解，还需要确定这些优化目标的权重，通过公式f(x)=w1*f1(x)+(1-w1)f2(x)在所得Pareto解中选择最优方案，式中：w1表示目标函数f1(x)的权重值。测试分析中取w1=0.5所得的f(x)对算法进行测试分析。收敛时间72.010212 s，目标函数1等于94，目标函数2等于228，综合目标函数f(x)等于161。