让思想不“静止”——高中生数学创新思维的培养

江苏省常熟市王淦昌中学 唐洁琼

一个民族、一个国家进步与兴旺的基石是创新，而作为承载着新时期现代化建设的青少年，创新是他们必须具备的基本素养。创新能力与创新思维是人们有目的地改造和重组已有知识，创造出具有个人或者社会价值的新颖的、独特的“产品”的一种能力。创新并非是学生与生俱来的能力，创新思维需要教育者在学习过程中对学生有针对性地进行着力培养。高中数学课堂为培养高中生的创新思维提供了一个良好契机，数学被称之为“思维的体操”，通过数学学习，引导、激发学生的创新思维从潜能引向显能，是每位教育者的职责所在。在课堂教学中，只有当学生面对一些能够引发他们兴趣，且在他们能力范围内的问题时，他们才会产生积极探究、大胆创新的意识。同样也只有让高中生亲历知识的形成过程，他们才会学会如何创造性地学习与思考。基于此，本文从有效情境创设、引导自主探究、拓展创新思维途径等方面，对如何在高中数学课堂培养学生创新思维进行了深入研究与思考。

一、创设有效情境，给创新思维提供契机

创新必须是一种主动行为，但主动行为的“诱因”是兴趣。如同一棵幼苗想成为参天大树，就需要阳光、土壤、水分等多种因素的“催发”一样，高中生创新思维的形成与发展，也需要特定的环境，一个能够引起学生兴趣、引发他们观察与思考、激发他们创造创新动机的环境，这就是数学情境。数学情境的创设要结合班级、学生以及时间等综合因素而设计出的能够呈现出不同效果的学习环境，才能够真正激发起学生们兴趣与主观能动性。

如在“平面向量数量积坐标表示”的学习中，在引入新知时，老师可采取的情境创设很多：

一是可以通过恰当的实例引入，但可能会因为在解释模型上停留过多而造成主次不分。

二是从旧知“向量数量加减法”引发新知，但无法突出知识本质而有些不够深刻。

三是直接引入新知，让学生对知识目标一目了然，但却欠缺对学生自主能力的培养。

四是给学生提供一些材料，将发现问题的主动权交给学生。如提出问题：“从已知向量a=（1，3），b=（4，2）中，你们可以设计出哪些问题？”先鼓励学生自主解答，思考之后，他们从两个方向进行了尝试，一部分学生提出是不是可以求“向量的模”，还有一部分学生提出是否能求“两个向量夹角”，学生设计的这两个问题恰好就将本节内容的本质突显了出来。而这种自己提出问题并解决问题的形式，是很能够激发学生的创造热情的。

创新思维离不开兴趣引发的动力，在有效情境的创建中，老师还可以通过一些生活化情境，让学生们感受数学知识的实用价值，让他们认识到数学存在于生活中，创新是基于生活现实的发展。如在学习“导数概念”时，可以先让学生们观看跳水运动员的视频，然后根据视频设计生活化数学情境：“跳水运动员进行高台跳水时，起跳后时间t与运动员距水面相对高度h之间的函数关系是h（t）=-4.9t2+6.5t+10，问运动员在的时间段里，平均速度是多少？”同时还让学生们思考：这个时间段内运动员的状态是运动的还是静止的？用“平均速度”对运动员运动状态进行描述是不是合适？

通过计算学生们发现了一个相互“矛盾”的问题：平均速度是零，但运动员显然在这个时间段内是“运动”的，怎么回事：他们不由自主地陷入深思，即刻认识到对于物体运动的精确刻画，用“平均速度”并不客观，应该对某个瞬间的速度进行必要研究。这时教师马上给出“瞬时速度”的定义，并再次将问题抛向学生：“怎样计算瞬时速度？”将生活情境与问题情境结合在一起，给学生们创建有效的数学情境，引导学生用心去感受和体验数学思想，挖掘数学本质，在一个个问题的探寻与解决中，发展自己的创造性思维。

二、通过适当“留白”，引导学生自主创新

创新思维需要给学生一定空间让其自主发展，当他们在做某件事或者表达出某种想法时，说明他们的思维已经开始运转，这时教师对学生的行为与想法不必立刻进行评价和判断，而是通过适当“留白”和有效引导，让他们的思维呈现出自然发展的状态，有利于高中生多向思维、发散思维以及创新思维等多元化思维的提高。如例题：“假设等差数列{an}的前n项和是Sn，已知的等比中项是，等差中项是1，那么等差数列{an}的通项是多少？”由于该题相对简单，思路明晰，只要具有一定运算能力和方程思想即可解答，所以先让学生自主练习，并鼓励他们主动介绍思路和方法。马上就有学生想到了列方程组进行求解的方法，并公布了自己的解题过程和结果。这时教师不必即刻给出对或者错的判断，而是询问大家是否有不同意见和不同解法。课堂瞬间的宁静被打破，大家立刻又投入到思考中去，几分钟后有同学提出可以从存在的规律中去考虑数列判断它为等差数列，使计算量大大减少。这个提法引起了很多同学的赞同，也激发了其他人的探究激情，而这种积极的情感与思维正是创新思维的萌芽，此时乘胜追击，鼓励学生们继续创新，很快又有学生找到了简洁方法，即先通过等差数列性质将数列中某项和前几项和之间的关系进行表达，再解题就简单了很多。至此，创新思维带给学生们莫大的快乐与自信，这种积极的情感体验会让创新成为一种习惯，伴随其学习和生活始终。

三、借助资源整合，拓展创新思维途径

所谓创新，就是指思维不被禁锢于一个范围之内，而是用开阔的视野、多元的角度去在常规中寻求不寻常的方法与思路。很多教育者习惯将学科独立起来实施教学，这在某种程度上就是对思维的一种局限。数学是所有学科的基础，同时它与诸多学科之间又是密切相连的，通过学科资源的有机整合，给学生开辟更多创新渠道，是发展创新思维的一条新路径。

如在学习“不等式”时，有例题如下：已知a，b，m∈R+，如果a＜b，证明

面对这种典型例题，大多学生通过分析法或者是比较法就能够进行证明。然而通过资源整合，对目标结构进行适当重组与调整，就会改变学生们对问题进行考查与解决的角度与思路：

1.平面几何角度。如图，将矩形ABCD的四边均延长m，那么从矩形面积特征中就会得出“ab+bm＞ab+

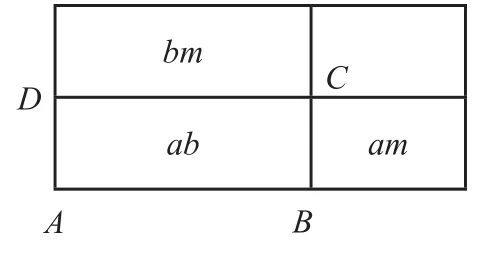
4.化学角度。可将“看作“a个单位溶质存在于b个单位溶质里，质量百分数比加入m个单位溶质后的质量百分数低”。

……

对于这种题型的“变身”，学生们感到十分新颖有趣，认识到了各个学科之间存在的神秘联系，同时也学会了如何打破数学思维的局限性，从多个角度去开拓自己的思路，积极展开更多的创新思维活动。

创新思维其实是每个高中生都具备的一种潜能，但这种潜能是在教育者有效引导和强化训练中被激发出来的，并在不断的自我努力中得到升华的。在数学课堂中让学生入其境、予其时、任其行，其目的都是给学生以足够的机会和空间实现自我突破与发展。如果将思想比作一盘琴键，那么它静止时，就是在等待着敏捷手指的撩拨，而教育者就是一支“金手指”。数学教育者要学会用这支“金手指”去触动高中生创新思想的琴键，通过一片奇异的颤动而奏出一串乐意，奏响一曲美妙的“思维之旅”。