例析数学思想在解决函数问题中的渗透

江苏省盐城市实验高级中学高三（28）班 周文昊

数学思想是从数学内容中提炼出来的数学知识的精髓，是将知识转化为能力的桥梁，它有着普遍的应用意义，是历年高考的热点与难点。函数作为高中数学的重要组成部分，有关函数问题的解题中蕴含着丰富的数学思想方法。同学们在解题的过程中若是能够充分、灵活地运用数学思想方法，则可以使得许多问题快速、准确地得到解答。笔者结合做题实践，现将一些常见的数学思想方法通过函数例题的形式给同学们做一简单呈现，希望为读者了解数学思想方法以及对函数的学习提供一些帮助。

一、换元思想

换元是通过引入一个或者多个新元来替换题目中的旧元，从而创造条件，化难为易，变繁为简，使得问题得以解决。

分析：本题看似无从下手，但是通过分析可以发现4x是2x的平方，因此本题可以转化为关于2x的二次函数，利用换元法将2x替换出来。

解：令t=2x，因为x∈[0,2]，所以t=2x∈[1,4]。

评注：本题属于可转化为二次函数的最值问题的求解，这类题型一般与换元法相结合，但是要注意换元后的新函数的定义域的变化对解题的影响。

二、数形结合思想

所谓数形结合思想，是指在一定条件下将数与形进行相互转化。借助图形的性质将那些抽象的概念、复杂的数量关系变得直观形象，以便于探究解题思路或找到问题的结论。数形结合思想方法具有直观性与灵活性等特点。

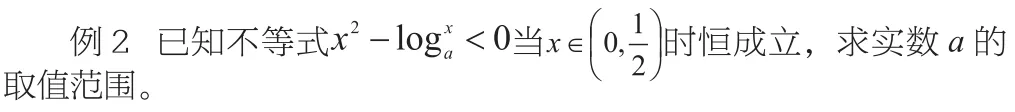
评注：“以形助数”是已知两个图象交点问题求参数范围常用的方法，解决此类问题的关键在于准确作出不含参数的函数图象，并标清关键点，对于含参数的图象，要注意结合条件作出符合题意的图形。

三、分类讨论思想

分类讨论思想具有明显的逻辑特点，利用分类讨论的方法解决问题的实质就是将整体问题化成部分来解决。注意要化成部分问题，就要增加题设的条件。

即x（x+a-2）≤0，

由f '（x）=0得x=0或x=2-a，又因为0＜a＜4，

所以：当 0＜a＜2 时，由 f '（x）＜0 得 0＜x＜2-a；

当a=2时，f '（x）≥0；

当 2＜a＜4 时，由 f '（x）＜0 得 2-a＜x＜0。

综上：当0＜a＜2时，f（x）的单调减区间为（0，2-a），

当2＜a＜4时，f（x）的单调减区间为（2-a，0）。

评注：本题中求单调减区间的实质是解含参数的不等式f '（x）≤0。分类讨论的标准是f '（x）=0的两个根0和2-a的大小。

四、转化与化归思想

转化与化归思想方法是数学中最基本的思想方法，使用该思想方法来解题时的原则是将所求问题转化为熟知的、易解的或者已经解决的问题来进行求解。

则对任意a∈（0，+∞），g（a）＞0恒成立的充要条件是g（0）≥0，

评注：变量分离是求解含参问题的重要方法。

五、函数与方程思想

所谓函数思想是指用运动和变化的观点，集合与对应的思想去分析和研究数学问题中的数量关系。方程思想是分析数学问题中变量间的等量关系。

分析：函数在某一点的切线斜率就是在某点处的导数值，因此可以利用函数的切线的斜率及点 列方程组，求出a，b。

由切点 在直线y=3x+1上可得-2+b=7，解得b=9。

评注：导数的几何意义为该点处的切线斜率。

六、构造思想

所谓构造思想就是指在对问题进行透彻分析，对其实质进行深刻了解的基础上，借助于逻辑分析和长期积累的经验，发挥高度想象和创造性，将原来的问题从原来的模式转化为更能反映其本质特征的新模式的思想方法。

例6 假设x，y，z∈R，且x，y，z的绝对值均不大于1，求证：xy+yz+zx+1≥0。

分析：本题变量太多，且题设条件太少，若是直接通过不等式的相关知识直接求证，则困难较大。此时我们可以构造一个关于x的函数，利用函数的知识来解决可能要容易的多。

评注：本题在多个变量的情况下，应该抓住一个主元作为变量，根据题目给定的式子的基本特征，成功地构造出关于x的一次函数，再根据一次函数的图象性质，使问题简单化，也就容易对问题进行解决。

以上例举了几种常见的数学思想方法在函数问题解决中的运用。由于数学思想方法的运用非常广泛而且灵活，因此,要想熟练自如地运用它来解决数学问题，还需要同学们在平时的学习过程中学会归纳与总结。