基于一维距离像稀疏表达的无源假目标识别*

袁 伟

(中国西电子技术研究所，成都610036)

1 引 言

现代战争中雷达将面临着越来越复杂的电磁对抗环境[1]。针对雷达的破坏有硬杀伤和软杀伤两种方法。硬杀伤是指直接用反辐射弹等武器摧毁对方雷达装备，软杀伤则是使用干扰的方法使雷达无法正常工作，无法准确探测和跟踪目标。对雷达的干扰方式很多，按照干扰的来源分为无源干扰和有源干扰，按照干扰方式分为压制干扰和欺骗干扰。其中由于箔条和角反射器成本低廉、实施简单，最早也是最为广泛地作为无源干扰源。

箔条干扰分为压制式干扰和欺骗式干扰两类。飞机或舰船在对抗来袭导弹时经常使用箔条实施欺骗式干扰敌方的末制导雷达[2]。飞机或舰船投放箔条干扰后，当跟踪雷达分辨率较高或者箔条与目标的距离大于雷达分辨率时，箔条可以形成假目标欺骗干扰，造成雷达错误跟踪箔条假目标，丢失真实目标。另一种常用的无源干扰是角反射器。角反射器应用在海战场中对抗反舰导弹，利用舰船搭载角反射阵列，距离被保护目标一定距离，就可以产生角反射假目标，引导反舰导弹攻击搭载有角反射器的诱饵。

基于雷达一维距离像的干扰识别已有一定的研究：文献[3]通过仿真研究了箔条回波的特征；文献[4]提出了一种基于双基地多输入多输出(Multiple-Input Multiple-Output，MIMO)雷达信息冗余的新的范围欺骗干扰识别方法；文献[5]提出一种基于散射矩阵分解的雷达干扰识别方法；文献[6]提出一种自适应时频局部判别分析法的欺骗干扰识别方法；文献[7]提出一种基于频谱特征来识别干扰的方法；文献[8-9]研究了基于目标与干扰的微小运动特征的识别方法；文献[10]研究了基于多普勒特征的毫米波雷达干扰识别方法；文献[11]提出基于支持向量机学习的方法区分角反射器回波干扰。上述研究基本上是基于目标与干扰的雷达回波某些特征进行识别，除文献[11]外并没有通过大量目标与干扰的回波数据进行学习训练，一定程度上造成了方法的应用局限性。

本文针对箔条和角反射器对雷达实施的无源假目标欺骗干扰，利用雷达一维距离像信号，采用稀疏表达的方法进行目标一维距离像与干扰一维距离像的分类识别，达到抑制假目标的抗干扰目的。

2 无源假目标欺骗干扰典型作战样式

针对箔条与角反常用的作战样式，设计如下两种典型的作战想定。

2.1 想定1：干扰我方防空反击任务

敌攻击飞机攻击我地面目标或执行完任务撤退时，我防空雷达锁定跟踪敌空中目标，当敌飞机发现被跟踪锁定后，为掩护飞机可能会释放箔条，造成假目标干扰，此情况下敌飞机为减小被发现的概率，通常不会开启雷达，但敌目标会产生雷达回波。我方跟踪雷达可能会锁定上箔条假目标，敌方飞机趁机突防或逃跑。

2.2 想定2：干扰我方对海目标打击任务

我攻击飞机执行对海目标打击任务时，攻击雷达搜索锁定敌海面目标，如军舰、航母等，敌海面目标为防止被我方雷达锁定打击，可能在其周围一定距离外设置角反射器阵列，造成假目标欺骗干扰。我方雷达可能会瞄准假目标进行攻击，从而造成打击任务失败。

针对上述两种无源假目标欺骗干扰场景，我方雷达会同时接收到敌方目标与无源假目标干扰的回波信号，因此，如何针对目标与假目标干扰的回波脉冲信号进行识别分类是雷达抗无源假目标欺骗干扰的关键问题。由于目标对雷达回波呈现稀疏的强散射点，而背景的散射相对较少，所以相对于背景回波，目标回波具有显著的稀疏特征。另一方面，军事目标与典型无源假目标的回波散射点的分布、稀疏特征具有显著的可分性，因此，本文考虑使用稀疏表达的方法进行目标(主要指飞机和舰船)与无源假目标干扰(主要指箔条和角反射器)的分类识别。

3 稀疏表达原理

稀疏表达最早由Huber于1982年提出，由于其字典训练对计算能力提出较高要求，没有广泛地应用。Donohn等人在前人大量研究基础上于2006年正式提出压缩感知理论，指出若信号在某个变换域上足够稀疏，即使使用的采样频率低于奈奎斯特采样频率，同样也能恢复出完整的原始信号。

稀疏表达是伴随着压缩感知理论发展起来的。设y∈n是一个列信号，D∈n×K(n≪K)是由向量集合(d1,d2,…,dK)组成的向量空间，并且D是过完备的，称D为冗余字典。y可以表示成D的线性组合，用矩阵表示即y=Dx，其中x=(x1,x2,…,xK)T是系数向量。若系数x中大部分值为0或者接近0，就认为其线性组合是一个稀疏表达。对原始信号进行稀疏表达之后，可以通过稀疏系数x和字典进行重构D，假设重构后的信号为

(1)

稀疏表达就是在稀疏度(稀疏表达系数的非0个数)满足一定范围时，寻找重构误差最小的系数x，或者在重构误差满足一定范围时，寻找非0个数最小的系数x，通常前者的受限方程是一个NP难问题，可以通过后者逼近，即满足方程

(2)

式中：x*是y的稀疏表示，ε表示重构误差的容限。

4 干扰与目标的稀疏字典训练

稀疏字典是一组过完备基组成的空间，常用的固定字典有离散余弦字典(Discrete Consine Transform,DCT)、小波字典，甚至可以用随机矩阵作为稀疏字典。上述字典是普适字典，用其对特定类别的信号进行稀疏表达，表达的稀疏系数并不能达到最优稀疏程度，或者在一定稀疏度下其重构误差并不能最小化，其稀疏表达的优势与信号类别没有关联，不利于利用表达后的稀疏系数进行识别。通过特定类别的信号集进行字典学习，得到平均重构误差最小化的稀疏字典。由于最终得到的稀疏字典实际上是该类别信号的线性组合，因此，利用该字典对同类信号进行稀疏表达，在稀疏度相同的情况下其重构误差更小，而利用该字典对其他类目标的信号进行稀疏表示，其重构误差明显较大。

稀疏字典训练的目的是寻找使得x尽量稀疏的D*，即求解方程

(3)

通常要求参与训练的目标信号数量大于信号维度，构成超完备字典。假设目标的雷达回波信号有N组，训练集为Y={y1,y2,…,yN},yi∈n，利用K-奇异值分解(K-Singular Value Decomposition,K-SVD)方法进行稀疏字典训练，训练算法描述步骤如下：

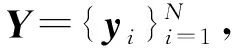
输出：稀疏字典D。

Step1 从Y中随机选取K个信号初始化字典D(0)=(y1,y2,…,yK)，初始化循环计数器J=1，初始化重构误差err(0)=INF。

Step2 重复Step 2～10，直至满足J≤IterMax，或者err(J-1)=Err。

Step3 利用正交匹配追踪(Orthogonal Matching Pursuit,OMP)方法计算原始信号Y通过稀疏字典D(J-1)的稀疏表达系数。X(J-1)={x1,x2,…,xN}，即对信号yi，求解其稀疏表达稀疏xi为

Step4 更新字典D(J-1)：对于字典D(J-1)的每一列dk(k=1,2,…,K)，执行Step 5～10。

Step5 定义ωk={i|1≤i≤N,xk(i)≠0}为一个索引向量，其中xk表示X(J-1)的第k行，定义Ωk为N×|ωk|的矩阵，它在(ωi(i),i)处的值为1，其他值为0。

Step6 计算不考虑原子dk时字典的重构误差矩阵Ek=Y-∑j≠kdjxk。

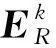
Step10 设置J=J+1。

利用同类别信号训练的字典，对同一类别的信号进行稀疏表达，由于字典学习到了该类信号的共同特征，表达同类信号的能力强，即稀疏表达系数的非0个数更少，或者重构误差更小；反之，表达异类信号的能力弱，对异类信号的重构误差就大。

鉴于上述原因，针对第2节的想定场景，考虑同时利用目标(飞机和舰船)与无源干扰源(箔条和角反射器)的雷达回波信号进行各自的稀疏字典的训练，分别得到目标稀疏字典为Dt和假目标干扰稀疏字典为Dn。即在想定1中利用飞机的雷达回波数据训练目标稀疏表达字典，利用箔条干扰源的雷达回波数据训练假目标干扰稀疏表达字典；在想定2中利用舰船的雷达回波数据训练目标稀疏表达字典，利用角反射器的雷达回波数据训练假目标干扰稀疏表达字典。

5 干扰与目标的雷达一维距离像稀疏重构

利用稀疏字典对信号进行表达，求解表达后的稀疏系数，就是寻找在一定稀疏度下使得重构误差最小的稀疏系数，或者寻找在满足一定重构误差时使得系数的稀疏度最小化，即求解方程

(4)

利用训练好的稀疏字典，使用OMP算法对需要表达的信号进行稀疏表达与重构，算法步骤描述如下：

输入：稀疏字典D，信号样本y，稀疏度T0。

输出：稀疏表达系数x。

Step1 初始化t=1，系数x0=0∈K，残差r0=y-Dx0=y，索引集合S0=∅。

Step2 计算p=DTrt-1，寻找p最大的分量索引j0，更新St=St-1∪{j0}。

Step3 计算xt=D(St)-1y，其中D(St)表示取D中对应St的索引列，计算残差rt=y-D(St)xt。

Step4t=t+1，若t≤T0结束，否则返回Step 2。

Step5 获得系数x(St)=xt，x其他位置为0。

OMP算法在信号稀疏分解时的每一步对选择的全部原子进行正交化处理，这使得在相同稀疏度要求的情况下，算法的收敛速度更快；另一方面，稀疏表达系数的稀疏度和重构误差相互制约，算法只采用稀疏度作为循环终止的条件时，通过正交分解总能找到一组稀疏表达系数，只是其重构误差不能达到最小而已。但本文就是要在相同稀疏度的情况下，比较不同类别目标数据学习的字典对同一未知类别目标的信号的稀疏表达能力，即重构误差的大小。因此，在不限制重构误差的情况下，任意完备字典必能对信号进行一定程度的表达和稀疏重构，表明该重构算法是鲁棒的。

上述方法应用在想定1中，对于未知的雷达回波数据y，分别利用飞机目标的稀疏字典Dp和箔条干扰假目标的稀疏字典Dc进行重构，得到未知信号的两种稀疏表达系数xp和xc，即

(5)

(6)

6 目标与假目标干扰的分类识别

基于稀疏表达的目标与干扰假目标的雷达一维距离像信号识别流程如图1所示。

图1 基于雷达回波的目标与假目标干扰识别示意图Fig.1 Flow chart of recognition of target and jamming based on radar echo

用两种稀疏字典分别对未知的雷达输入信号进行稀疏表达，分别计算两种稀疏表达的重构误差et和en：

(7)

计算两种重构误差的比值:

e=et/en。

(8)

当两次重构误差的差值达到一个阈值时，认为该雷达一维距离像是目标，即在想定1中是飞机，在想定2中是舰船；否则是假目标干扰，即在想定1中是箔条假目标，在想定2中是角反射器假目标。

7 仿真分析

7.1 训练测试数据

在实际应用中，首先要根据情报等先验信息确定作战区域中可能存在的敌方目标和无源干扰的类别，然后建立目标与无源干扰的雷达回波数据库，利用回波数据库进行字典学习和目标与无源干扰的识别。涉及多样目标时，必须为每类目标建立训练数据进行字典学习。实验中针对上述两个作战场景进行仿真分析。

针对作战想定1，利用电磁仿真软件计算，设置雷达的信号带宽为120 MHz，回波添加的全频谱白噪声，分别获得飞机目标与箔条的雷达一维距离像数据，通过与实测数据比较，仿真数据与真实数据的误差小于3%，飞机与箔条的回波信号的全频段信噪比从实验组1～3依次为5 dB、3 dB、0 dB。训练测试样本如表1所示。

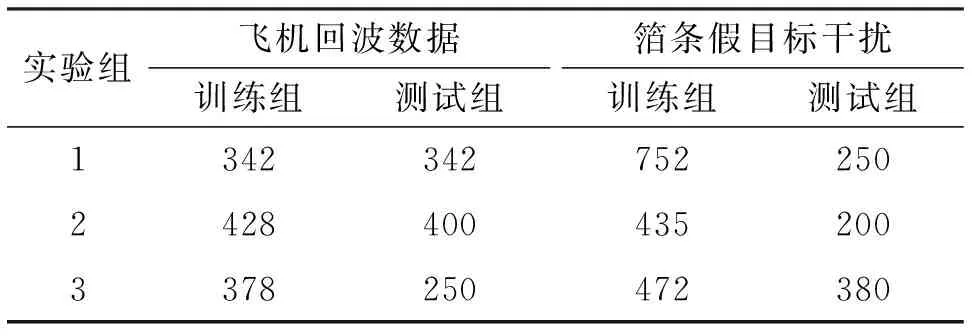
表1 飞机与箔条训练测试样本Tab.1 Training and test samples of aircraft and chaff

针对作战想定2，在某外场进行实验，分别获取了海上某中型机动目标与角反射器的雷达一维距离像实测数据，机动目标与角反射器的回波信号的全频段信噪比从实验组1～3依次为5 dB、3 dB、0 dB。训练测试样本如表2所示。

表2 舰船与角反训练测试样本Tab.2 Training and test samples of ship and corner reflector

7.2 基于雷达一维距离像的飞机与箔条假目标干扰识别

分别利用预处理后的飞机与箔条回波数据集，基于稀疏字典学习算法训练飞机和箔条干扰的稀疏字典。字典的原子长度为100，原子个数为400。由于原子个数远大于原子维数，故构成了冗余字典。

为了验证稀疏字典的重构能力，分别使用各自的稀疏字典对各自的回波进行重构。首先使用飞机的稀疏字典重构飞机信号，其重构信号如图2所示，此样本重构误差设置较小，迭代次数较多，故红色的重构信号基本与飞原始的回波信号差别较小。

图2 飞机稀疏字典重构的飞机目标信号Fig.2 Aircraft echo reconstructed by sparse dictionary of aircraft

上述重构产生的重构误差如图3所示，可见平均误差在0.2%以内。

图3 飞机稀疏字典重构飞机回波信号的误差Fig.3 Reconstruction error of aircraft echo signal by sparse dictionary of aircraft

同样验证箔条干扰的稀疏字典的重构能力，使用箔条干扰字典重构箔条回波，其重构的信号如图4所示。

图4 箔条干扰字典重构的箔条回波信号Fig.4 Chaff echo reconstructed by sparse dictionary of chaff jamming

上述重构产生的重构误差如图5所示，平均误差在1.1%以内。

图5 箔条干扰字典重构箔条回波的误差Fig.5 Reconstruction error of chaff echo by sparse dictionary of chaff jamming

分别使用箔条的稀疏字典和飞机的稀疏字典对实时回波进行稀疏表达，计算两种表达下的重构误差。图6(a)所示为使用飞机稀疏字典和箔条干扰稀疏字典对箔条回波信号的重构误差，可以看出对于箔条回波信号，飞机稀疏字典对它的重构误差普遍大于箔条干扰稀疏字典对它的重构误差。图6(b)所示是使用飞机稀疏字典和箔条干扰稀疏字典对飞机目标的回波信号的重构误差，可以看出对于飞机目标回波信号，飞机目标的稀疏字典对其的重构误差普遍小于箔条干扰稀疏字典对其的重构误差。

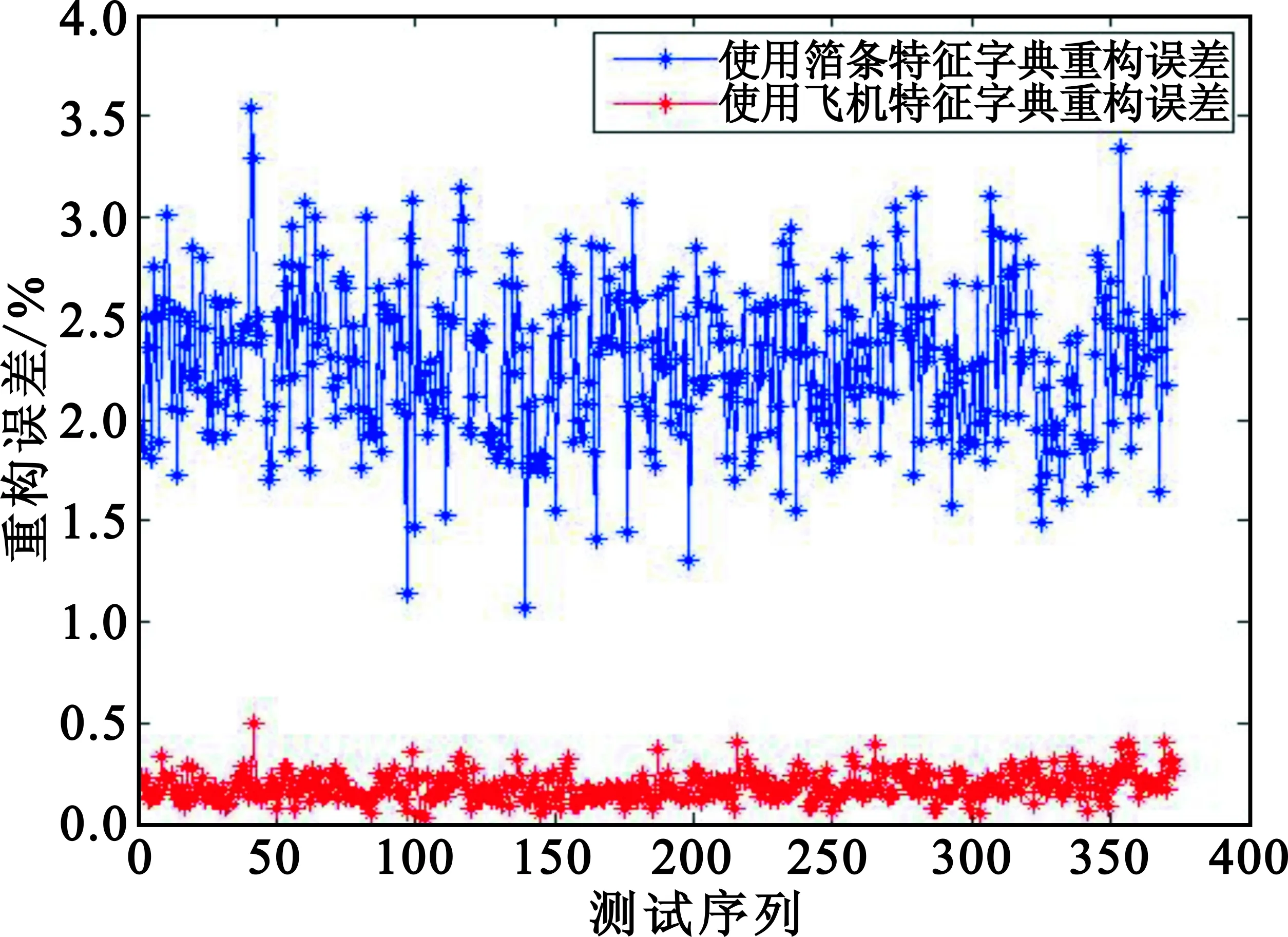
(b)飞机图6 两种稀疏字典重构箔条和飞机的误差Fig.6 Reconstruction error of chaff and aircraft by two sparse dictionaries

鉴于上述仿真结果，在实时的回波信号识别中，计算两个稀疏字典对未知回波的重构误差比，根据重构误差比判断回波信号是箔条假目标还是飞机目标。如图7所示为测试组1的结果，使用两种稀疏字典分别对飞机和箔条干扰的回波进行稀疏表达并计算重构误差比，结果表明两种稀疏字典对飞机回波的重构误差比远大于1，而对箔条假目标回波的重构误差比小于1。这是因为利用飞机回波数据学习的字典对飞机信号的重构能力强，而对箔条信号的重构能力弱;相反，利用箔条回波数据学习的字典对箔条信号的重构能力强，对飞机回波的重构能力弱。

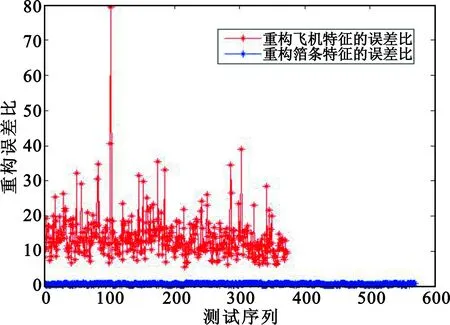
图7 两种稀疏字典对飞机和箔条的重构误差比Fig.7 Reconstruction error ratio of aircraft and chaff by two sparse dictionary

7.3 基于雷达一维距离像的舰船与角反假目标干扰识别

分别使用舰船的雷达一维距离像数据集和角反的雷达一维距离像数据集训练各自的稀疏字典，并使用各自的稀疏字典对各自的回波信号进行重构来验证字典的稀疏表达能力。首先使用舰船的稀疏字典重构舰船回波，其重构误差如图8所示，误差基本小于1%。

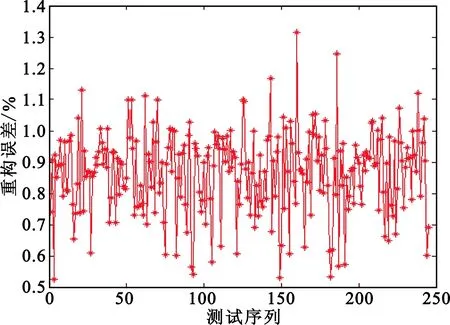
图8 舰船的稀疏字典重构舰船回波的误差Fig.8 Reconstruction error of ship echo by sparse dictionary of ship

同样使用角反射器假目标干扰字典重构角反射器干扰信号，重构误差如图9所示，平均重构误差为1.2%。

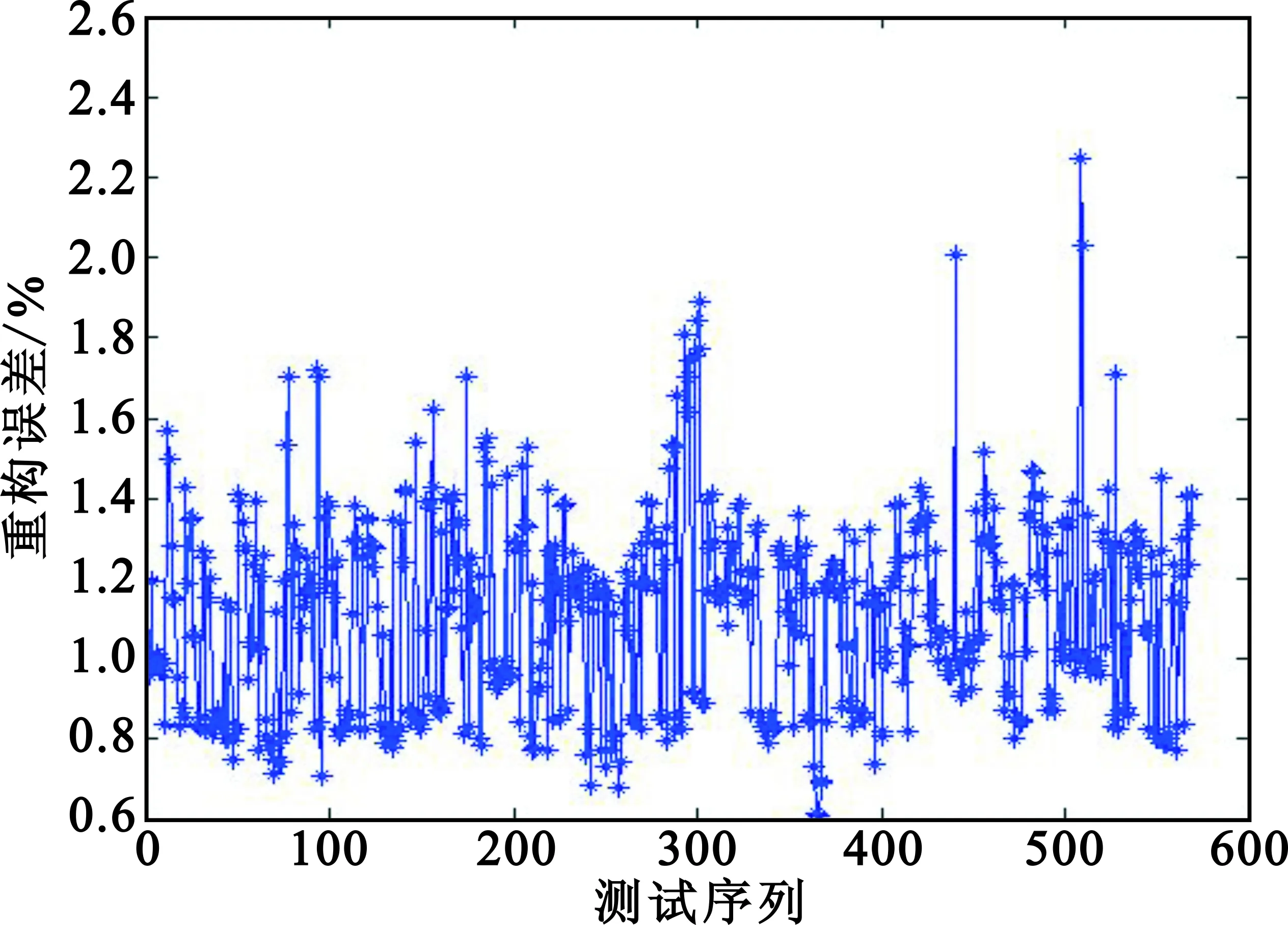
图9 角反干扰稀疏字典重构角反回波的误差Fig.9 Reconstruction error of corner reflector by sparse dictionary of jamming

测试表明同类目标的字典对同类目标信号的重构误差都在2%以内，而重构不同类目标的信号的重构误差则远远大于该误差。

使用两种稀疏字典对实时回波信号进行稀疏表达，计算两种稀疏表达下的重构误差比。如图10所示为测试组1的结果，两种稀疏字典重构舰船目标信号的误差比要远大于重构角反干扰信号的误差比。这是因为利用舰船回波信号学习的字典对舰船类目标信号的稀疏表达能力强，其重构误差就小，而对非舰船类目标如角反信号的重构误差就大；反之，利用角反干扰信号学习的字典对角反回波信号的重构能力强，而对舰船回波信号的重构能力弱。因此，可以利用目标与干扰字典对未知回波数据的重构误差比来区分识别目标和干扰。

图10 两种稀疏字典重构舰船与角反回波的误差比Fig.10 Restructure error ratio of ship and corner reflector by two sparse dictionaries

在本实验测试集上目标与干扰信号的分类识别准确率统计如表3所示，在目标与干扰噪声比3 dB时箔条干扰识别准率达到90.5%，角反干扰识别准确率达到91.2%。

表3 箔条与角反的识别率Tab.3 Recognition rate of chaff and corner reflector

8 结束语

本文通过研究关注目标与无源假目标干扰的雷达一维距离像信号的稀疏特性，提出了基于稀疏表达的方法进行雷达一维距离像数据的目标与无源假目标干扰的识别。该方法可以根据实际工程应用中雷达可能面向的目标与无源干扰，通过仿真或实测获取目标和干扰的回波数据，经过数据积累后进行训练学习，进而在实战中进行无源干扰识别。所提方法在解决高分辨率雷达抗无源干扰问题上具有一定的实用价值。

本文方法未考虑目标与雷达之间的相对位置以及目标的姿态等对回波数据的特征产生的影响，后续将针对目标或无源干扰的多角度多姿态回波数据，设计角度和姿态自适应的目标和干扰特征字典，提升目标与干扰识别的角度和姿态适应能力。