多参数优化深度置信网络的滚动轴承外圈损伤程度识别

刘浩，熊炘，周辰，刘荣刚

(上海大学 机电工程与自动化学院,上海 200072)

机械设备在运行过程中，滚动轴承除了承受能量转换零部件传递的交变载荷，还要承受工况波动引起的随机载荷，容易发生损伤失效。因此，滚动轴承损伤的模式识别是滚动轴承故障诊断与寿命预测的关键。

故障识别和分类的准确性依赖于先验特征的提取，而先验特征的确定需要故障诊断领域的专家经验[1]。文献[2]通过改进蛙跳算法优化BP网络的权值和阈值，用以诊断滚动轴承早期故障。文献[3]提出了基于Laplacian双联最小二乘支持向量机的半监督识别方法，应用于少样本条件下滚动轴承早期故障的诊断。对于损伤位置不同的滚动轴承及其性能退化过程，可通过改进的超球结构多类SVM实现准确识别[4]。文献[5]利用PSO算法优化支持向量机参数，获得了更高的识别准确率，且其结果不受载荷波动的影响。上述有监督式聚类方法主要针对特定轴承损伤类型设计学习模型，获得了较高的识别准确率。另一方面，自组织映射[6]、隐马尔科夫链[7]、独立成分分析[8]等无监督聚类方法通过学习输入向量间的内在结构关系诊断轴承损伤，但相同样本空间中的不同样本集易导致对样本总体概率分布估计的波动。

滚动轴承承受的交变冲击载荷是导致轴承滚道表面损伤的主要原因。表面损伤从点蚀开始，随着损伤区域的增加演变成分布式损伤[9-10]，考虑此因素对动力学特性的影响，建立滚动轴承外圈损伤动力学模型以获取反应不同外圈损伤程度的动力学响应历程。利用深度置信网络(Deep Belief Network, DBN)的自适应特征学习能力[11]实现不同损伤程度的无监督识别。同时，为了降低人为选择DBN结构参数对识别准确率的影响，利用模拟退火算法(Simulated Annealing Algorithm, SAA)优化网络参数，实现自动高准确率的轴承状态识别。通过开展不同信噪比仿真数据试验，以及齿轮箱轴承数据试验，验证上述方法对轴承外圈损伤程度的识别准确性与算法稳定性。

1 无监督学习方法

1.1 DBN无监督学习

深度置信网络的特征学习由多个限制玻尔兹曼机(Restricted Boltzmann Machine, RBM)实现。每层RBM中包含显性神经元(输入)v和隐性神经元(输出)h，显性神经元与隐性神经元之间通过权重W连接，偏置分别为c和b。在同一个RBM中，相同类型的神经元之间互不干扰，其结构如图1所示。

图1 RBM结构Fig.1 Structure of RBM

RBM的能量函数可以表示为

(1)

式中：vi，hj分别为显性神经元i和隐性神经元j的二值变量；ci，bj分别为相应神经元的偏置；wij为两类神经元之间的权重。V和H分别表示显性和隐性神经元的单元数。RBM训练的目的是获取最大概率产生特定样本的概率分布。对于一组特定的训练样本，其显性和隐性神经元联合分布为

P(v,h)=e-E(v,h)/Z，

(2)

式中：Z为配分函数。

显性单元vi和隐性单元hj被激活的概率分别为

(3)

(4)

式中：δ(x)为激活函数，δ(x)=1/(1+e-x)。

测量结果一致性评价 同一医师两次重复测量、两名医师分别测量ADC值及rADC值的ICC>0.81，一致性较好(表1)。

通过极大似然函数求导得到W，并使当前样本在该分布下的概率最大，即

(5)

式中：(·)data，(·)model分别为样本和模型分布的期望。实际情况下，(vihj)model很难求解，因此选用对比散度算法[11]训练RBM。

一个DBN结构可由若干层RBM串联组成，其中浅层RBM的输出层作为更深层RBM的输入。对于数据xm(m=1～M)，首先训练第1层RBM，通过 (5) 式优化网络参数使网络结构误差最低。然后将第1层RBM的输出h1作为下一层RBM的输入v2。之后各层RBM均由同样的方法训练，且每一层RBM中的隐性神经元均是对当前层显性神经元无监督特征提取的结果，这样就避免了人为因素的影响。所有的RBM训练完成后，通过BP算法自上而下对整个DBN网络参数进行优化，以提高学习准确率。

1.2 多参数优化DBN的无监督学习

为降低人为选择网络参数导致学习准确率的波动，实现DBN的自动识别，利用SAA的同时对RBM的层数和各层RBM中隐性神经元的个数进行优化，得到趋于全局样本空间下的最高准确率。通过SAA实现的多参数优化避免了使用穷举法耗费的大量计算时间，同时降低了人为网络参数选择带来的准确率波动。

首先，将网络参数初始化；其次，将原始时域数据直接输入DBN进行模型训练；然后，在完成学习任务后随机调整网络参数，进行第2次模式识别；最后，将2次识别的错误率进行比较，根据比较结果确定SAA下一次识别时的DBN结构参数，这一机制如图2所示。

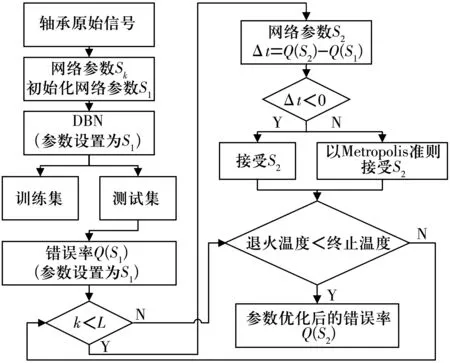
图2 多参数优化DBN方法步骤Fig.2 Steps of multi-parameter optimized DBN method

2 仿真信号识别

2.1 外圈损伤滚动轴承动力学仿真

利用 (6) 式表示的五自由度滚动轴承模型[10]研究外圈损伤轴承的动力学特性，使用四阶龙格库塔法求解非线性振动方程，数值仿真得到不同损伤分布弧长对应的加速度响应历程。仿真轴承型号为SKF 6004-2RSH。

，(6)

(7)

每个滚子因轴承内、外圈在水平x和垂直y方向上发生的相对位移而产生变形，形变量可表示为

δj=(xs-xp)cosφj+(ys-yp)sinφj-

c-βj[Cd(φ)+Aj]+R(φ)，

(8)

式中：xs，xp和ys，yp分别为轴承内、外圈在x，y方向上的位移。除此之外，形变计算还考虑工作游隙c、表面波纹度R(φ)和表面损伤Cd(φ)的影响。

初始点蚀由瞬时冲击或持续工作导致的材料疲劳引起，而后沿着滚道扩展为具有一定分布角度的分布式损伤。外圈损伤形貌的几何特征描述是损伤动力学仿真是否准确的关键。因此，外圈损伤建模为具有一定深度的浴盆曲线，其深度Cd为10 μm，浴盆的粗糙表面由Gauss白噪声信号通过低通滤波确定[12]。

图3 滚动轴承正常及外圈损伤仿真信号Fig.3 Simulation signals of normal and outerring defected rolling bearing

2.2 仿真信号的无监督学习

将待识别加速度时域信号直接输入DBN。为保证DBN学习时对数据量的需求，每类时域样本时长为26.4 s，分别分割为1 000个样本。按照表1的样本组合将信号拆分为不同数目的训练集和测试集，分别测试不同信噪比条件下本方法的识别准确率和稳定性。原始时域信号进行归一化处理，以避免幅值不同导致的分类偏差。

表1 仿真信号的平均识别准确率Tab.1 Average identification accuracy for simulation signals

以训练集和测试集样本数量分别为800和200为例，在20 dB背景噪声下，调整RBM层数(1～4)与各RBM中隐性神经元个数(100～800)进行测试，DBN的识别结果如图4所示，图中的矩形框反映20次分类识别准确率偏离均值的程度，矩形框内的虚线表示特定网络参数下20次分类识别准确率的均值，矩形框外的上下黑色线段为20次分类识别准确率的最大值和最小值。从图4可以看出：对于1层RBM，当隐性神经元个数为400时识别准确率最高，达到93%，且此参数条件下20次试验准确率均超过90%；对于2层RBM，识别准确率最高可达98%，且每种参数条件下20次试验的识别准确率均超过了94%；当RBM层数为3和4时，平均识别准确率均超过97%。另外，通过改变信噪比，采用不同训练集和测试集的组合方式，对该方法的稳定性进行测试，结果见表1(结果取相同参数设置下20次试验的平均值)。

图4 DBN轴承仿真信号识别Fig.4 Identifications for simulation signals of bearing using DBN

为减小DBN中RBM层数以及各RBM中隐性神经元个数对识别准确率的影响，利用SAA算法对网络参数进行优化，在全局样本空间下达到最高识别准确率。初始化DBN参数S1，初始温度T0=1 000 ℃，终止温度T=100 ℃，步长L=20。最终，网络参数优化后的识别准确率见表1。由表可知，在不同信噪比，不同训练集和测试集样本组合方式下，SAA优化后的DBN结构均达到了更高的识别准确率。

3 齿轮箱轴承损伤分类试验

试验台如图5所示，采用二级平行轴减速齿轮箱结构，由电动机、齿轮箱、数据采集卡、变频器、加速度传感器以及速度传感器组成。

图5 齿轮箱试验台示意图Fig.5 Diagram of Gearbox test rig

轴承型号为SKF 6004-2RSH，内径20 mm，外径42 mm，球组节圆直径40 mm，球径9 mm，球数为9。输入轴转速为2 700 r/min，输出轴为空载。利用KD 1005L单轴加速度传感器采集轴承加速度信号，采样频率为25.6 kHz。在齿轮箱输入轴的输入端安装2种不同外圈损伤程度的滚动轴承以及正常轴承分别进行试验。试验时，轻微损伤的分布弧长为0.3 mm，深度为0.2 mm。较严重损伤的分布弧长为0.8 mm，深度为0.2 mm，如图6所示。

图6 滚动轴承外圈损伤Fig.6 Outer ring defects on rolling bearing

从3种状态轴承的加速度数据中各选取1 000组样本构成待分析样本集合，每组样本的时长为0.2 s。3种状态轴承的功率谱密度曲线如图7所示，三者在特征频率构成及能量分布上无明显差异。试验样本数据集合的划分见表2，试验中训练集和测试集中的样本顺序随机排列。

图7 齿轮箱轴承加速度信号功率谱密度Fig.7 Power spectral densities of bearing acceleration signals from gearbox

训练集&测试集样本数为800 & 200时，不同RBM层数及各RBM中隐性神经元个数不同条件下的识别结果如图8所示。从图中可以看出，所有试验的识别准确率均超过了90%。在不同训练集和测试集的样本划分下对DBN稳定性进行测试，获取平均识别准确率；然后，利用SAA对DBN结构参数进行优化，经过优化后得到平均识别准确率，测试结果见表2。由表可知，不同训练集&测试集组合对识别准确率的影响较低，而参数优化后的DBN针对不同样本组合识别稳定性更高，抗干扰能力更强，识别效果也更佳。

图8 齿轮箱轴承损伤识别Fig.8 Damage identification for gearbox bearing

表2 齿轮箱轴承信号的平均识别准确率Tab.2 Average identification accuracy for signals in gearbox bearing

在相同条件下，选择标准差、偏度、偏度系数、峭度、峭度系数、6阶中心矩、标准化6阶中心矩和峰值共8种特征作为待学习的候选特征，利用BP网络进行分类试验。通过选取不同候选特征构建特征向量，分别测试不同特征向量特征构成，以及不同特征向量长度下的轴承损伤程度识别准确率。试验准确率在相同参数条件下通过50次独立试验结果求取均值得到，结果如图9所示(图中3条柱状代表确定特征个数后，从原始8种待选特征中随机抽取特征，依次形成的不同特征构成的3组特征向量)。从图中可以看出，BP网络最高识别准确率为86.43%，最低准确率仅为62.54%，对低信噪比的齿轮箱信号识别结果比较差；而最小互熵值表明，BP网络的识别结果受特征选择影响较大，稳定性差。

图9 BP网络试验分类准确率与稳定性Fig.9 Accuracy and stability for test classfication of BP network

对比分析可知：以实际齿轮箱信号作为试验数据时，由于试验数据信噪比低，使用传统的特定特征提取方法时，BP网络故障识别准确率较低，且识别准确率受特征数量和类型的影响较大；文中方法则适用于信噪比较低的轴承信号，可得到较高识别准确率，且识别结果的稳定性更高。

4 结束语

提出了一种基于多参数优化DBN的无监督学习方法，以外圈损伤为例，设置不同信噪比、训练集、测试集组合，利用五自由度轴承动力学模型及齿轮箱轴承损伤分类试验验证了该方法的高识别准确率和稳定性；通过SAA对DBN结构参数进行全局优化，减小了DBN 结构参数对识别准确率的影响，从而达到对特定任务的最高识别准确率。

上述结果只是在不同轴承外圈损伤程度下得到了较高识别准确性，在一定程度上可以说明该方法对轴承单部位损伤识别的有效性。然而，实际工况下的轴承损伤往往分布于多个部位，对轴承其余单个部位乃至多个部位的损伤程度识别仍需继续研究。