高速角接触球轴承热分析及试验验证
2018-07-26金燕刘少军张建阁
金燕,刘少军,张建阁
(1.常州工程职业技术学院,江苏 常州 213164;2.中南大学,长沙 410083)
角接触球轴承能同时承受径向和轴向载荷,广泛应用于直升机主减速器中,其工作性能直接影响主减速器的使用寿命[1]。
由于摩擦、润滑油黏性剪切的作用,使得角接触球轴承内部产生的热量迅速升高,热膨胀或收缩产生的热应力对轴承寿命有一定影响,温度过高时轴承会发生胶合失效,严重时甚至会发生咬死的现象[2-4]。因此,有必要对轴承的摩擦发热量进行研究。
国内外很多学者通过研究滚动轴承的发热和散热机理来获得滚动轴承的温度场,进而帮助合理设计和正确使用轴承,并为轴承系统故障和失效分析提供依据。文献[5]提出了滚动轴承的热源和对流换热系数的计算模型,利用ANSYS对滚动轴承进行了有限元分析,得出了滚动轴承的温度和热变形,为研究滚动轴承的热变形和游隙问题提供了参考和依据。文献[6]将套圈滚道生热视为移动热源,建立了高速圆柱滚子轴承的二维瞬态温度场计算模型,运用ANSYS的APDL语言编制了温度计算的参数化程序。文献[7]采用有限元法对角接触球轴承温度场进行了仿真,并通过试验测试了不同转速和载荷下轴承温度分布与轴向热位移。
现以某型直升机主减速器角接触球轴承为研究对象,研究轴承摩擦发热量的计算方法和对流换热系数的选取,基于ANSYS软件对轴承进行稳态热分析,研究径向力与转速对轴承稳态最高温度的影响,并进行试验验证。
1 温度场分析
1.1 摩擦发热量计算
工程上经常采用Palmgren发热量计算方法[8]计算滚动轴承的摩擦生热,轴承摩擦力矩为
M=Mf+Mv,
(1)
Mf=f1Fβdm,
Fβ=Fa-0.1Fr,
f1=0.000 3(P0/C0)0.33,
式中:Mf为载荷力矩,N·mm;Mv为与润滑油有关的摩擦力矩,N·mm;dm为轴承平均直径,mm;Fβ为合成力,N;Fa为轴向力,kN;Fr为径向力,kN;f1为与轴承结构和载荷有关的系数;C0为额定静载荷,N;P0为当量静载荷,N;f0为与润滑方式和轴承类型有关的系数;μ为润滑油运动黏度,mm2/s;n为转速,r/min。
轴承摩擦发热量为
H=0.001Mω,
(2)
式中:ω为轴承角速度,rad/s。若速度采用r/min单位,则
H=1.047×10-4Mn。
(3)
1.2 对流换热系数计算
热量传递主要包括3种形式:热传导、热辐射和热对流。对轴承而言,传导和对流散热量之比为0.05左右,说明润滑油带走了绝大部分的热量,主要的传热方式是各零件表面与其周围润滑油间发生的热对流,其他2种形式可忽略。轴承零件表面与润滑油的热对流可描述为
Hv=hS(T1-T2),
(4)
式中:Hv为轴承发热量;h为对流换热系数,受流体速度、热导率等因素影响;S为换热面积;T1为轴承零件表面温度;T2为润滑油温度。
轴、轴承和轴承座中各个开放表面的对流边界条件如图1所示。轴承采用喷油润滑方式进行润滑与散热,设润滑油的定性温度为入口油温,计算滚动轴承的对流换热时,对不同零件需要选取定型尺寸来计算流体平均速度和其他参数。
图1中,设内圈表面的对流换热系数为h1,外圈表面的对流换热系数为h2,轴承向润滑油传热的对流换热系数通过(5)式确定;内圈内表面与轴外表面的对流换热系数为h1/3;外圈两端面的对流换热系数为h2/3[6];轴承座外表面的对流换热系数为h3,与空气进行自然对流换热,定型尺寸为壳体的外壁直径;轴内空气与外界交换较少,因此认为轴的2个端面和轴内表面为绝热面,发热量q=0;qi和qe分别为内、外圈发热量。
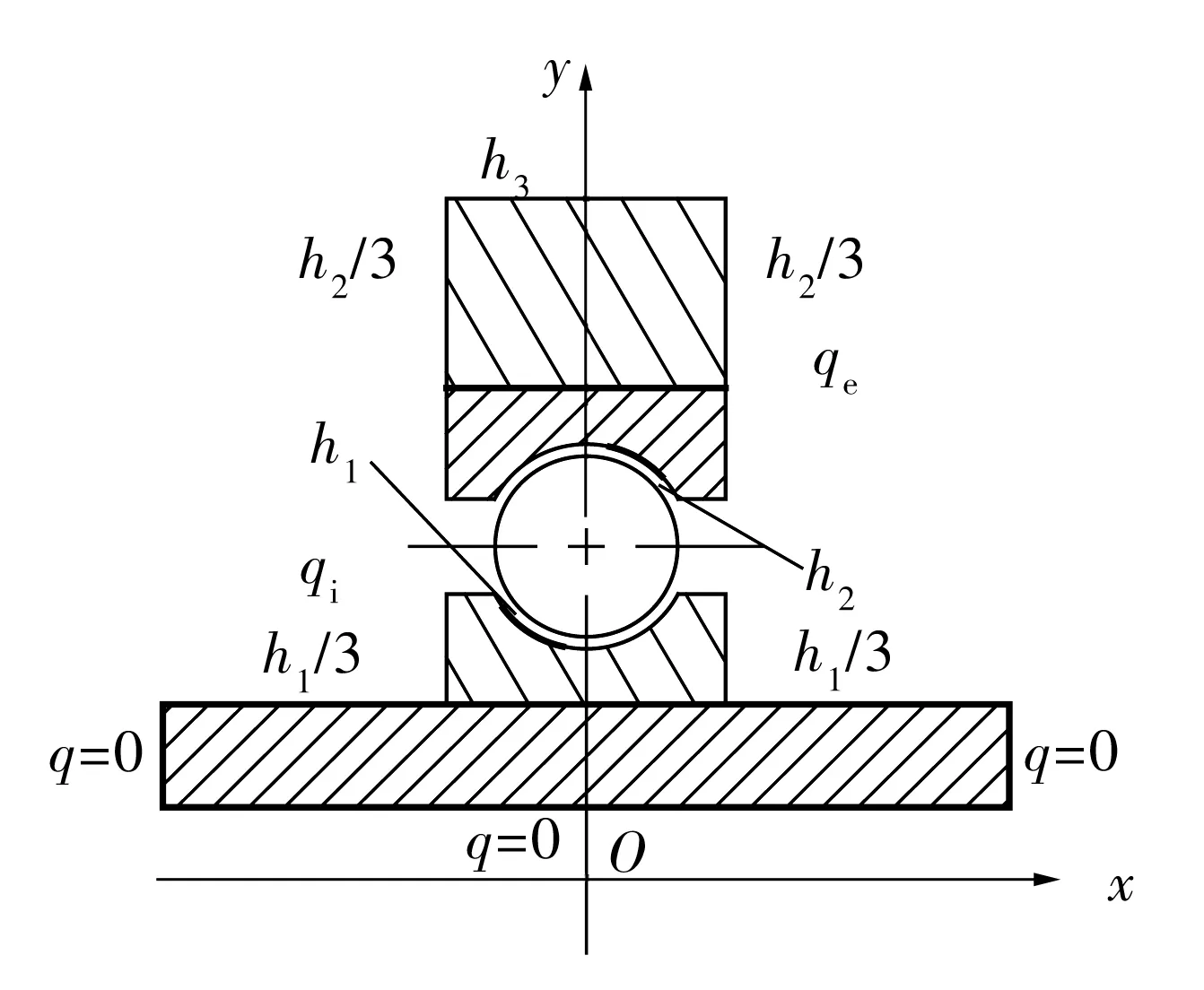
图1 球轴承二维热分析模型示意图Fig.1 Diagram of 2D thermal analysis model of ball bearing
(5)
式中:k为润滑油导热系数;Pr为润滑油的Prandtl系数。1)计算轴承座内表面与润滑油间的传热时:vs取保持架速度的1/3,x取轴承座内径;2)计算轴承与润滑油之间的传热时:vs为保持架转速,x取球组节圆直径。
保持架转速为
(6)
式中:D为轴承公称外径;α为初始接触角。
润滑油的Prandtl系数为
(7)
式中:ρ为润滑油密度;Cp为等压比热容。
轴承座外壳表面与空气间的对流换热系数为
(8)
式中:T为外壳温度;Ta为环境温度;ka为空气导热系数;Dh为外壳直径;va为气流流速;μa为空气运动黏度。
1.3 ANSYS稳态热分析
采用热有限元法,在ANSYS软件中进行稳态热分析,假设节点温度不随时间变化,建立稳态分析能量平衡方程为
KT=Q,
(9)
式中:K为传导矩阵;T为节点温度矢量;Q为节点热流量矢量。
ANSYS分析中,根据模型参数、材料热性能参数以及所施加的边界条件,分别生成K,T和Q。
2 轴承温度场仿真分析
2.1 轴承基本参数
某直升机主减速器角接触球轴承参数见表1。轴承零件材料均为GCr15。
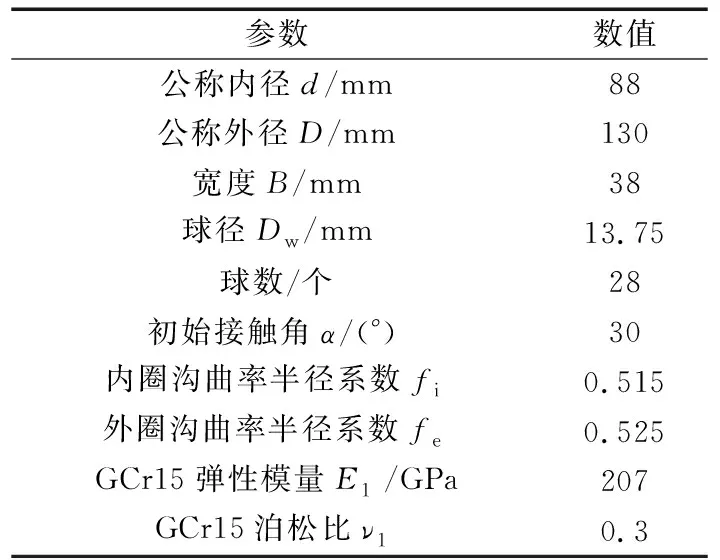
表1 双列角接触球轴承参数Tab.1 Parameters for double row angular contact ball bearing
2.2 轴承有限元稳态热分析
将材料的热物理性能添加至材料库,在轴承发热量及对流换热系数研究基础上,对轴承施加热载荷和热边界条件。当Fa=6 kN时,不同径向力Fr及转速n下轴承发热量见表2。由表可知:随着径向力和转速的增大,轴承发热量均不断增加。
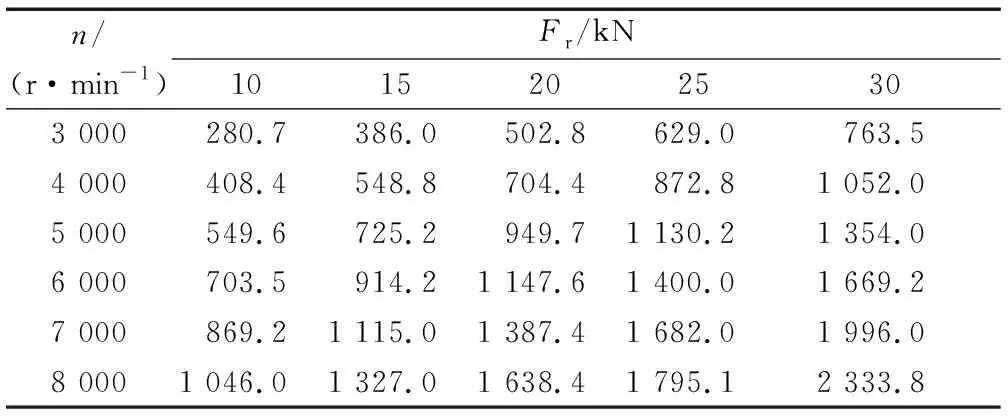
表2 不同工况下轴承发热量Tab.2 Heat generation of bearing under different operating conditions W
Fa=6 kN,Fr=25 kN,n=7 000 r/min时,轴承稳态热分析结果如图2所示。由图可知,轴承在运转过程中,内圈与钢球接触区域的温度最高,达123 ℃;钢球温度为117 ℃;外圈与钢球接触的区域温度最低,为113 ℃。如果摩擦发热量不及时散出,累积到一定程度会导致温度过高、接触面应力增大,使得摩擦加剧,在如此恶性循环下轴承最终会发生失效。为使轴承更好地散热、避免热疲劳的发生,在进行轴承润滑和冷却设计时要重点关注内圈与钢球接触区域的润滑和冷却。

图2 轴承稳态热分析结果Fig.2 Steady state thermal analysis result of bearing
径向力、转速对轴承最高温度的影响分别如图3、图4所示。从图中可以看出:随着径向力、转速的增加,轴承稳态最高温度均显著上升,且转速对最高温度的影响更明显。这是因为径向力的增加会增大轴承的整体载荷摩擦生热量,而转速的增加不仅增大了载荷摩擦生热量,还会导致润滑油黏性摩擦生热量。

图3 轴承稳态最高温度随径向力的变化曲线Fig.3 Variation curve of the highest temperature of bearing under steady state with radial forces
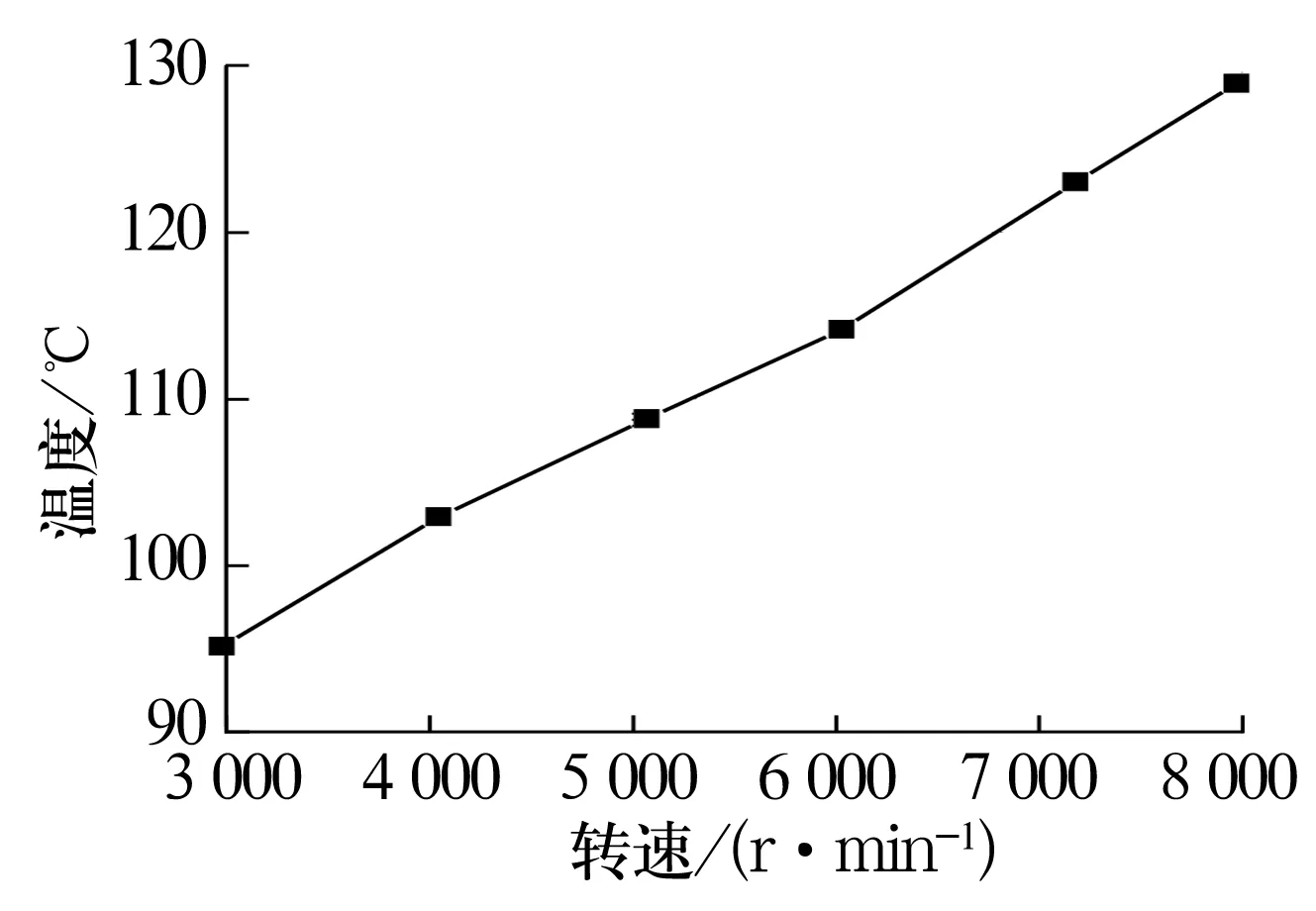
图4 轴承稳态最高温度随转速的变化曲线Fig.4 Variation curve of the highest temperature of bearing under steady state with rotational speeds
3 热分析试验验证
试验装置如图5所示。主要包括试验台(轴与轴承座接触处装有轴承)、润滑系统与测控系统,其中试验台包括试验齿轮轴承箱、加载与传动等试验部件。

图5 试验系统的总体结构Fig.5 Overall structure of test system
试验采用红外热像仪测量温度,同时在特殊点处采用铂电阻测温(误差很小,可视为标准温度,但测量不便)进行对比校正。测量点的分布如图6所示,图中标号1,2,3处为红外热像仪测温点,标号4为利用铂电阻Pt100测温时安装铂电阻的孔。

图6 测温结构及测量点Fig.6 Temperature measuring structure and measuring points
试验环境温度为20 ℃,转速为1 000 r/min,扭矩为120 N·m。试验测得的轴承稳态温度分布云图如图7所示,内、外圈及钢球的温度分别为77,72.5,74 ℃。相同工况下轴承稳态温度场仿真云图如图8所示,仿真得到的内外圈、钢球的温度分别为73.5,68,70 ℃。

图7 试验中轴承稳态温度分布云图Fig.7 Nephogram of steady state temperature distribution of bearing during test

图8 轴承温度场仿真分布云图Fig.8 Nephogram of temperature field simulation of bearing distribution
由图7、图8可知:
1)轴承的最高温度发生在内圈与钢球接触处,其次是内圈与轴接触处,一般情况下外圈较二者的温度低。故在考虑轴承润滑和热疲劳时,应重点关注内圈的状况。
2)仿真结果和试验结果存在一定误差,但误差在允许范围内,验证了轴承温度场的有限元仿真方法在一定条件下是可行的。
为进一步验证和分析轴承温度场仿真结果的准确度,改变轴承转速和扭矩(环境温度为20 ℃)重复试验,将测得的内圈最高温度与仿真结果进行对比,如图9所示。由图可知,在误差允许范围内,仿真结果和试验结果吻合度较高。由于理论计算中对热量传递进行了简化,忽略了热辐射和热传导,因此仿真结果略小于试验结果。
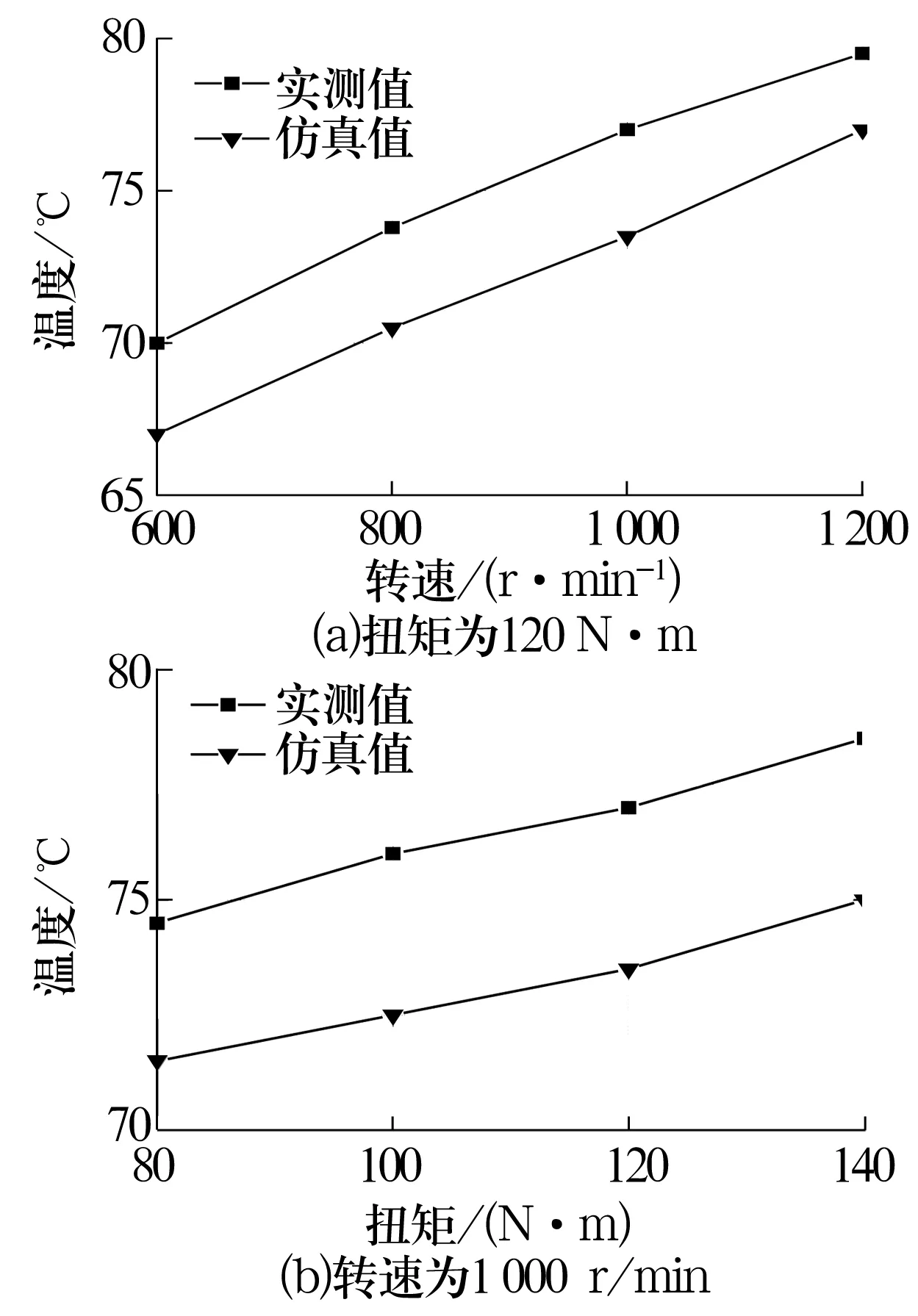
图9 内圈最高温度仿真结果与试验结果对比Fig.9 Comparison between simulation results and test results of the highest temperature of inner ring
4 结论
1)轴承最高温度位于内圈,其次是钢球,一般情况下外圈的温度较低。
2)随着径向力、转速的增加,轴承稳态最高温度均显著上升,且转速对最高温度的影响更明显。
