非均匀L型阵列的联合对角化二维DOA估计算法
2018-07-26杨晋生
项 杨 杨晋生
(天津大学微电子学院,天津 300072)
1 引言
波达方向(direction of arrival, DOA)估计是阵列信号处理的重要内容之一,受到了众多学者广泛的关注[1]。其中,二维DOA估计算法被广泛应用于各种形式的阵列,例如双平行均匀线阵[2-3],三平行均匀线阵[4-5],L型均匀线阵[6-13]等。L型阵列具有形式简单且能够提供较好的角度估计性能等优点。因此,学者们提出了大量基于L型阵列的二维DOA估计算法。文献[8]通过构建匹配矩阵实现了方位角和俯仰角的自动配对,但它需要类似谱峰搜索的运算。文献[11]解决了角度兼并问题,在欠定条件下可实现角度估计且能够自动配对。
上述的算法有一个共同的特点,即阵元间距小于等于半波长。扩展孔径可以有效地提高阵列的分辨率和角度估计精度,但会出现角度模糊的现象。文献[15]提出了一种获得高精度无模糊方向余弦的方法,因此有效地提高了DOA估计性能。当包含方向余弦估计信息的DOA矩阵具有相同的对角线元素时,它不能解决奇异点问题,即不能获得正确的方向余弦估计值。在此基础上,文献[16]提出的算法将扩展孔径的阵列应用到xoy平面的两个双平行阵列中,且使用传播算子算法[17]降低了计算复杂度,但仍不能解决奇异点问题。针对特征值相等时的角度配对失效现象,文献[18]提出一种基于子空间正交的新配对方法,故能够解决部分奇异点问题。
为了解决扩展孔径的二维DOA估计存在的奇异点问题,本文提出了非均匀L型阵列的联合对角化二维DOA估计算法。首先,从延时互相关矩阵中提取信号子空间。然后,通过联合对角化方法获得自动配对的两种方向余弦,即高精度模糊的方向余弦和低精度无模糊的方向余弦。值得注意的是,即使DOA估计矩阵具有相同的对角元素,也可以获得正确的方向余弦。最后,为了实现解模糊,以无模糊估计值为参考,从模糊估计值中得到高精度无模糊的估计值。因此,提出的算法解决了在扩展孔径的二维DOA估计中的奇异点问题,并且在欠定条件下具有良好的表现性能。
符号:(·)T,(·)*,(·)H和(·)+分别表示转置,共轭,共轭转置和伪逆运算。⊙和⊗分别表示 Khatri-Rao (KR)积和Kronecker积。E[·]表示统计期望,arg(·)表示相位。IM是一个维数M×M单位矩阵。diag{·}是由列向量元素组成的对角矩阵。blkdiag{·}表示块对角化。 circshift(·,m)是沿着行向右循环移动m个单位。
2 阵列结构和数据模型

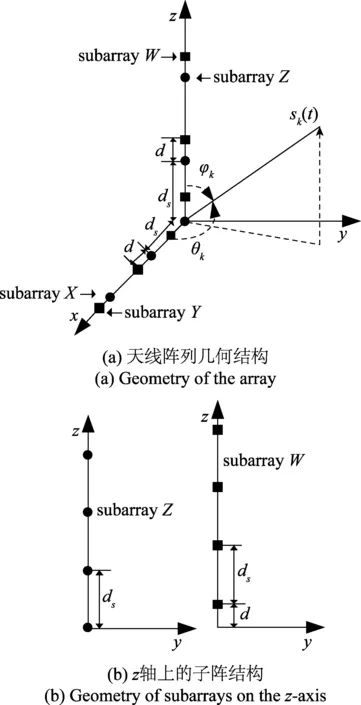
图1 阵列插图Fig.1 Illustration of array
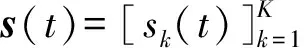
ρε(t)=Aεs(t)+nε(t)
(1)



(2)
此外,其他两个子阵的阵列流型矩阵如下
(3)

3 提出的算法
所提出的算法主要包括三个部分。首先,根据KR运算构造延时互相关矩阵。其次,在延时互相关矩阵和选择矩阵运算得到对角矩阵的基础上,通过联合对角化方法得到自动配对的两种方向余弦估计值,即高精度模糊的方向余弦估计值和低精度无模糊的方向余弦估计值。最后,通过解模糊方法得到高精度无模糊方向余弦估计值,进一步得到方位角和俯仰角。
3.1 延时互相关矩阵的构造
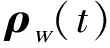
(4)
因此,根据KR运算得到的延时互相关矩阵表示如下
(5)

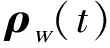
(6)
(7)
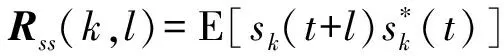
(8)
根据式(8), 对应的阵列形式如图2所示。
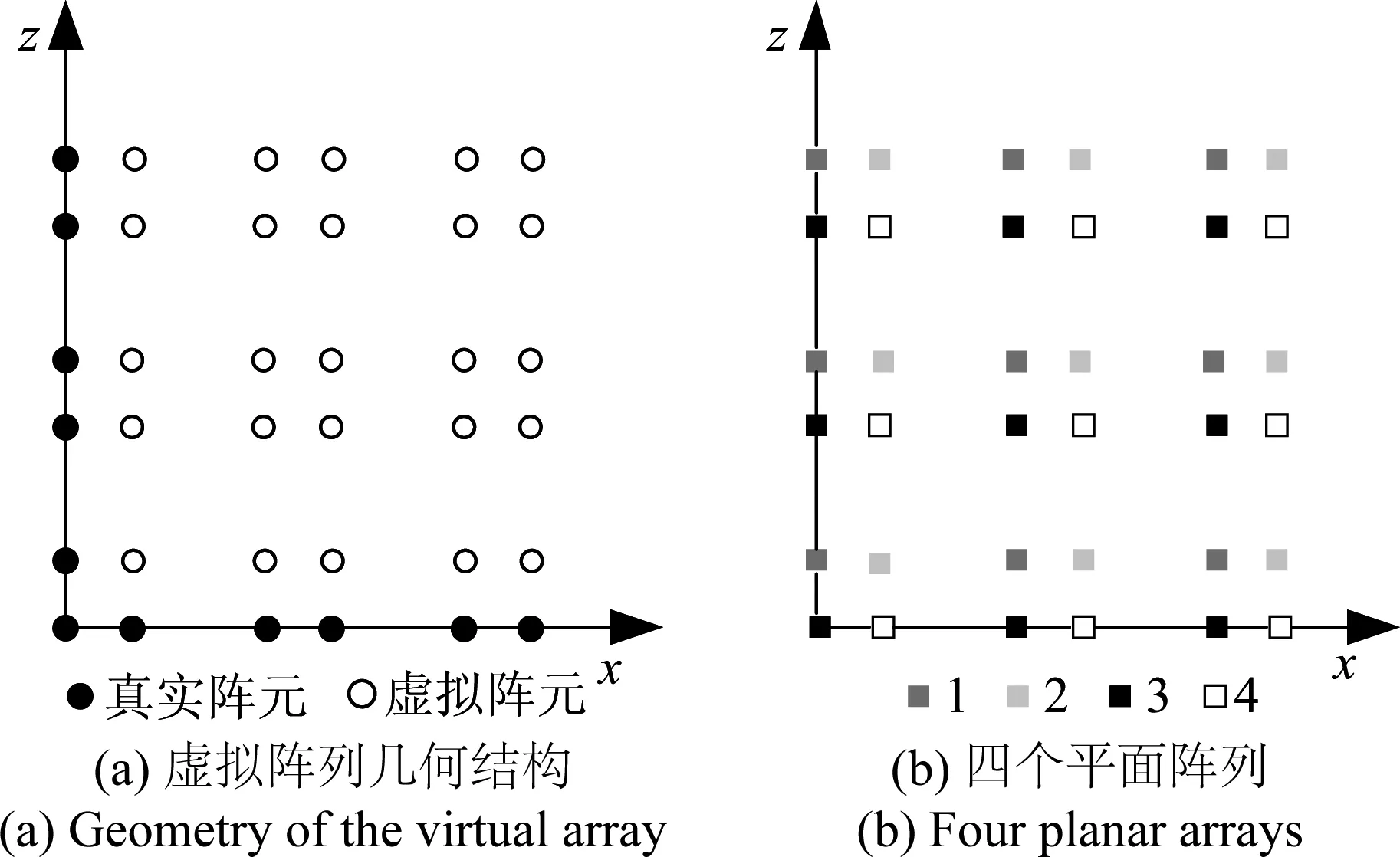
图2 阵列划分Fig.2 Partition of array

3.2 方向余弦的估计
通过对R进行奇异值分解(Singular Value Decomposition,SVD),可以得到信号子空间Us以及具有K个较大奇异值的对角矩阵Λs
(9)
从式(8)和图2(b)易知,平面阵列1与2、1与3、3与4以及2与4之间的间距均为d,且四个平面阵列内部相邻阵元间距为ds,故Us包含高精度模糊的方向余弦信息以及低精度无模糊的方向余弦信息。
平面阵列1与2,3与4之间均包含x轴低精度无模糊的方向余弦信息。因此,构造选择矩阵G1=[G01,G00,G02,G00],用于选取与平面阵列1、3相对应的Us中两个子块;G2=circshift(G1,M2)用于选取与平面阵列2、4相对应的Us中的两个子块。其中,G00=02M2×M2,G01=[IM2;0M2],G02=[0M2;IM2]。因此,包含x轴低精度无模糊的方向余弦对角矩阵可表示如下

(10)
式中,T=A+UsΛ1/2是一个酉矩阵。

(11)
四个平面阵列中均包含x轴高精度模糊的方向余弦信息,对应对角矩阵表示如下
(12)
式中,G5=I4M⊗[IM-1,0(M-1)×1],G6=circshift(G5,1),Φ(θ)=diag{ej2πdscos θ1/λ,...,ej2πdscos θK/λ}。

(13)
式中,Φ(φ)=diag{ej2πdscos φ1/λ,...,ej2πdscos φK/λ}。


(14)

(15)
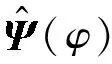
3.3 二维DOA估计的实现
(16)

(17)

根据以上的分析,第k个信号的方位角和俯仰角估计表达式如下
(18)
因此,我们可以得到自动配对的俯仰角和方位角。所提出算法主要步骤概括如下:
(1)构造式(7)所示的延时互相关矩阵。
(4)同理得到x轴上对应的两种方向余弦估计值。
3.4 算法分析
(1)角度估计
选择矩阵的维数直观地说明了所提出的算法可实现多达2M2个信源估计。因此,所提出的DOA估计算法在欠定条件下仍能实现方位角和俯仰角的估计与自动配对。同时,当俯仰角和方位角满足以下三种情况时,所提出的算法仍能获得正确的方向余弦估计:
情况 1θk=θp,cosφk≠cosφp±oλ/ds。
情况 2φk=φp,cosθk≠cosθp±oλ/ds。
情况 3θk≠θp,φk≠φp,cosθk=cosθp±oλ/ds,cosφk=cosφp±oλ/ds。
矿区生活区、选矿车间卫生间等生活污水经化粪池预处理后,与经隔油池处理后的食堂含油废水通过生活污水排水管道系统汇集,经一体化生活污水处理设施处理,达到标准后回用至生产回水水池。
其中,o为正整数表示两个来波信号在同一方向上的方向余弦估计值的差值为整数倍λ/ds。
证明如下:
由于R=ARss,故通过判断A的阶数即可得到R的阶数。
1)首先,判断A中互不相关行的个数。
由式(8)可知,阵列流型矩阵A中第k列中的不同行之间可能存在的关系分别为ej2πdcos φk/λ,ej2πdcos φk/λ,ej2πdscos θk/λ,ej2πdscos φk/λ。
当角度关系满足情况 1时,ej2πdscos θk/λ=ej2πdscos θp/λ且ej2πdcos θk/λ=ej2πdcos θp/λ,但由于cosφk≠cosφp±oλ/ds,故ej2πdscos φk/λ≠ej2πdscos φp/λ且ej2πdcos φk/λ≠ej2πdcos φp/λ,结合3.2中关于高精度模糊的方向余弦信息的选择矩阵的维数可知A中线性无关的行数至少为2M2。
当角度关系满足情况 2时,与情况1同理。
当角度关系满足情况3时,ej2πdcos θk/λ≠ej2πdcos θp/λ,ej2πdscos φk/λ≠ej2πdscos φp/λ且ej2πdscos θk/λ=ej2πdscos θp/λ,ej2πdcos φk/λ=ej2πdcos φp/λ,结合3.2中关于低精度无模糊的方向余弦信息的选择矩阵的维数可知A中线性无关的行数为至少为2M2。
2)其次,判断A中互不相关列的个数。
由式(8)可知, 阵列流型矩阵A中的各列之间并不存在线性关系,除非两个信号的方位角与俯仰角完全相同。故对于以上三种情况,A中各列始终线性无关。
综上所述,由于2M2>K,因此通过对R进行SVD分解可以得到信号子空间Us以及K个较大奇异值。
3)最后,文献[11]指出联合对角化可以有效处理角度兼并问题,因此所提出的算法在以上三种情况下仍能实现良好的角度估计。
(2)克拉美罗界
本文所提出算法的克拉美罗界(Cramer-Rao bound,CRB)[19]表达式如下
(19)

4 仿真实验
本文所提出算法的角度估计性能与文献[11]、文献[18]中的算法以及CRB[19]进行比较。所有信源的联合均方误差定义为
(20)

在所有的仿真实验中,所提出算法中子阵的阵元个数M=3,文献[11]中子阵的阵元个数为6,即L型阵列中共有11个阵元。由于文献[18]中算法应用的阵列结构不同,令其共包含13个阵元。此外,所有的仿真实验均进行1000次蒙特卡洛仿真。
仿真实验1
假设在一种欠定条件下,其中快拍数N、数据帧数L、信源个数K、信噪比SNR和扩展孔径ds分别为1000,500,18,30 dB,5λ。图3显示了欠定条件下所提出算法仍具有良好的估计性能。
如图3所示,当方位角和俯仰角满足情况1和情况2时,算法仍能够较好地实现方位角和俯仰角估计。当M=3时,本文提出的算法可实现多达18个信源估计。

图3 欠定条件下的角度估计性能Fig.3 Angle estimation performance in the underdetermined case
仿真实验2
当方位角和俯仰角满足情况3时,验证所提出算法的有效性。假设有K=2个信号入射到天线阵列,两个信号分别为(90°,60°),(120°,90°)或(65°,33°),(85°,60°)。即o1=1,ds=2λ,cos 60°=cos 90°+1/2且cos 90°=cos 120°+1/2;o2=1,ds=3λ,cos 65°=cos 85°+1/3且cos 33°=cos 60°+1/3。其他实验条件均与仿真实验1相同。图4为角度估计值分布散点图。值得注意的是文献[18]中的算法不能实现此种情况下的角度估计。
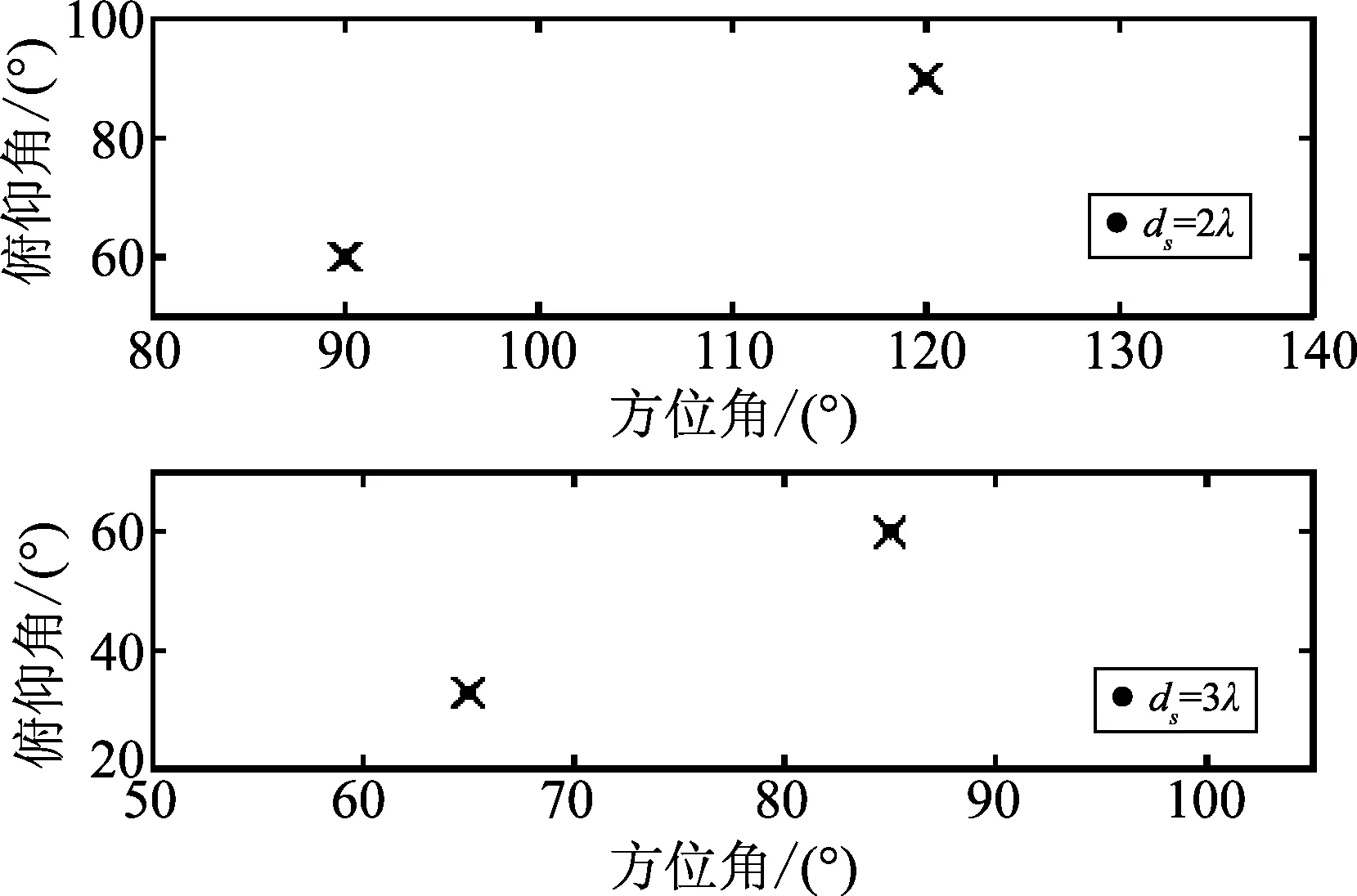
图4 情况3下的角度估计性能Fig.4 Angle estimation performance for Case 3
从图4可以看出,当方位角和俯仰角满足情况3时,所提出的算法能够清晰地分辨这两个来波信号。根据文献[20]中的定理1可知,式(10)~(13)所示的四个对角矩阵中没有相等的对角元素时,算法才可获得正确的方向余弦估计值。在扩展孔径的二维 DOA估计算法中随着ds的增大,存在o,ds使得cosθ1(cosφ1)=cosθ2(cosφ2)+oλ/ds成立。因此,实验1和实验2证明了所提出的算法已解决了在扩展孔径的二维DOA估计算法中的奇异点问题,且角度估计性能较好。
仿真实验3


图5 RMSE随阵元间距的变化Fig.5 RMSE versus element spacing

仿真实验4
本实验研究所提出算法的估计性能随信噪比的变化情况。其中,N=200,L=50,ds=8λ。假设有K=4个等功率非相关信号入射到天线阵列,信号的方位角和俯仰角分别为(60°,90°),(60°,110°),(80°,90°)和(80°,110°)。算法的角度估计性能随信噪比的变化情况如图6所示。

图6 RMSE随SNR的变化Fig.6 RMSE versus SNR
仿真实验5
本实验研究所提出算法的估计性能随快拍数的变化情况。其中SNR=0 dB,其他实验条件均与仿真实验4相同。算法的角度估计性能随快拍数的变化情况如图7所示。

图7 RMSE随快拍数的变化Fig.7 RMSE versus the number of snapshots
从图6和图7可以看出,随着SNR和快拍数的增加,两种算法的RMSE均减小,证明了所提出算法的有效性。值得注意的是,所提出的算法比文献[11]中的算法具有更好的角度估计性能。这是由于所提出的算法使用了扩展孔径的非均匀L型阵列,因此阵列孔径更大。
仿真实验6
本实验研究所提出算法对应不同角度的估计情况。其中快拍数N、数据帧数L、信噪比SNR和扩展孔径ds分别为200,10,15 dB,8λ。信号的方位角和俯仰角均在10°~80°之间以2°的步长变化。图8为对应不同角度的角度估计联合均方误差。
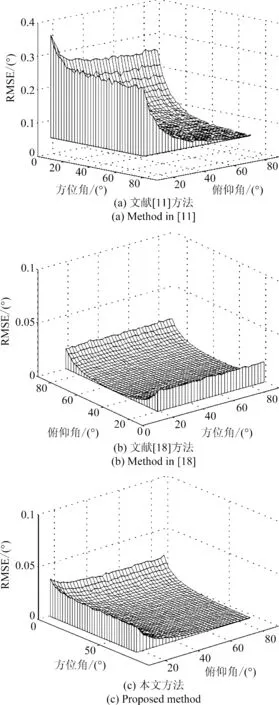
图8 不同方位角俯仰角的RMSEFig.8 RMSE for different azimuth-elevation angles

仿真实验7
由于文献[18]中的算法不能实现欠定条件下的角度估计,故研究其算法实现对两个信号源(60°,70°),(60°,80°)的角度估计。其中,信噪比SNR=15 dB。其他实验条件均与仿真实验4相同。图9为两种算法角度估计值分布对比散点图。由图9可知,与文献[18]中的算法相比,本文所提出的算法在解决奇异点问题时的估计性能更好。

图9 情况1下的角度估计性能Fig.9 Angle estimation performance for Case 1
5 结论
本文提出了一种扩展孔径的二维DOA估计算法。基于非均匀L型阵列,所提出的算法首先构造了四个延时互相关矩阵并对延时互相关矩阵进行奇异值分解得到了信号子空间。其次,利用选择矩阵从信号子空间中获得对角矩阵。再次通过联合对角化方法得到自动配对的精确和模糊的方向余弦估计值。最后,以低精度无模糊的方向余弦估计值为参考,从高精度模糊的方向余弦估计值中获取高精度无模糊的方向余弦估计值。所提出的算法能够实现方位角和俯仰角的自动配对。仿真结果表明所提出的算法有效地解决了扩展孔径的二维DOA估计算法中的奇异点问题。
