分布式独特码TDMA信号的检测和频率估计

侯骁宇 李天昀 杨司韩

(战略支援部队信息工程大学，河南郑州 450002)

1 引言

时分多址(TDMA)方式，通过将时间划分成互不重叠的时隙实现多个用户共享通信资源，实现同时通信，其具有通信容量大、频率利用率高等优点，因此广泛应用于各类通信系统中，例如 VSAT卫星通信系统、海事卫星系统、铱星系统等。TDMA通信系统通常具有以下特点：一是信号突发，持续时间较短；二是由于发送设备小型化导致接收信号质量较差，信噪比通常在12 dB以下；三是由于地面站和卫星之间的相对运动导致接收信号往往含有较大的多普勒频偏。因此，TDMA信号的突发检测和频偏估计往往有较高的要求。

目前针对TDMA信号的突发检测算法主要有以下几种：一是基于信号能量的检测[1-3]，通过检测窗内信号的能量来判断突发信号的存在性，这类方法具有良好的抗频偏性能，但对噪声敏感，不适合低信噪比条件下的检测；二是基于频域的检测方法，文献[4]提出基于循环谱的检测方法，利用信号的循环平稳特性进行突发检测，其优点是具有良好的抗噪声性能，但算法复杂，计算量大；三是独特字检测[5- 6]，通过利用独特码的自相关特性进行突发检测和帧同步，这类方法具有较高的检测精度，比较适合于有一定先验知识的信号的检测，但目前基于独特码的检测主要还是针对独特码分布在信号帧头的情况，对于新型的分布式独特码间隔插入的情况研究还较少。

大频偏信号通过匹配滤波器后信噪比会大幅降低,严重影响符号位同步、突发帧同步等后续处理。对突发检测后的信号在匹配滤波之前，首先要进行频率粗估计及校对，将频偏校正到符号速率的10%以内,为后续处理创造条件[7]。频率估计的经典算法有L&R算法[8]、Fitz算法[9]、M&M算法[10]、频谱细化估计算法[11-12]等，这些算法精度较高，但往往存在计算复杂、估计范围较窄等问题，因此一般应用在载波同步的小频偏的精确估计中。对于解决较大频偏的粗估计及校正问题，低计算复杂度、宽估计范围的算法更为合适。

本文基于一类新型的分布式独特码的TDMA信号，针对其独特码间隔插入的特点，采用延时共轭相乘的方式，对大频偏的该类信号进行突发起始检测和频率快速估计，分析了不同频偏、信噪比和码型结构对算法性能的影响，并从实际角度出发，对算法提出了进一步的改进和优化。仿真结果表明，检测算法精度较高，具有良好的抗频偏性能，频率估计算法估计范围宽，复杂度低，适合大频偏的快速粗估计和校正。

2 信号模型描述

TDMA信号通常采用MPSK调制方式，天线接收信号下变频后模型如下：

(1)

其中，ejφ(k)是第k个码元，φ(k)的取值为q·2π/M,(q=0,1,2,...,M-1)，Ar是码元波形幅度，T是码元持续时间，ω0是频偏，θ是初相，n(k)为复高斯白噪声。

TDMA信号具有独特的帧结构，通常由载波和比特定时恢复码(CBR)、独特码(UW)、站址识别码(SIC)、指令(OW)信号、勤务信号(SC)和消息数据组成。其中独特码是一种不容易为随机比特所仿造而造成错误检测的码组，以此作为突发的时间基准和帧同步依据[13]。独特码的长度一般在十几到几十比特不等。传统TDMA信号中独特码通常连续集中分布在数据突发的开始部分，其典型帧结构如图1所示。

图1 传统TDMA信号帧结构Fig.1 Traditional TDMA frame structure

a(i,j)=Auejφ(i, j),i=1,2,...,P,j=1,2,...,N

(2)

其中Au为常数，表示独特码的模长。ejφ(i, j)表示第i个独特码模块中第j个独特码符号。分布式独特码TDMA信号帧结构如图2所示。

图2 分布式独特码TDMA信号帧结构Fig.2 Distributed unique word TDMA frame structure

3 算法描述

3.1 独特码检测

当接收机接收到数据后，按照分布式独特码的结构对数据进行分段。以式(2)中分布式独特码TDMA信号为例，将接收数据分为P段，每段长度为L0个符号，取每段数据的前N个符号进行延迟共轭相乘得到新序列y，同时对本地独特码序列的每个插入模块中的N个独特码符号分别进行延迟共轭相乘得到序列b，将y与b进行相关求得相关系数。每进行一次相关运算后将接收数据向后移动一个符号，进行下一次的相关运算，最终得到整段数据的相关系数，经门限检测后输出突发起始位置。检测原理如图3所示。

接收序列和本地独特码序列分别延迟共轭相乘可得：

y(i,j)=r[(i-1)·L0+j+1]·r*[(i-1)·L0+j],

i=1,2,...,P,j=1,2,...,N-1

(3)

b(i,j)=a(i,j+1)·a*(i,j),

i=1,2,...,P,j=1,2,...,N-1

(4)

式(3)与式(4)相关，将式(1)、式(2)代入，忽略噪声影响可得：

(5)

其中Δψ(i,j)=[φ(i，j+1)-φ(i，j)]-[φ(i，j+1)-φ(i，j)]。

由式(5)可以看出，当本地独特码序列与接收序列对齐时，如果当前数据和独特码完全匹配，则对任意i和j均有φ(i，j+1)-φ(i，j)=φ(i，j+1)-φ(i，j)，即ejΔψ (i, j)=1，此时各项加和的模值最大，相关结果最明显。如果当前数据同独特码不匹配，由于传输数据和扰码的随机性，各单位矢量ejΔψ (i, j)相互抵消，实际相关结果将很小。并且因为采用了延迟共轭相乘的方式，频偏ω0的影响已经变为固定相偏ejω0T，不会对相关结果造成影响，因此大大提高了算法的抗频偏性能。

上述算法中参与相关运算的序列采用的是延时一个符号共轭相乘，即每个独特码段内部符号进行差分，考虑到分布式独特码间隔插入的特点，可以将延时增大到L0个符号，即相邻独特码段对应的符号进行共轭相乘后的结果作为相关运算的序列，则式(3)、式(4)分别改写为：

y(i,j)=r(i·L0+j)·r*[(i-1)·L0+j],

i=1,2,...,P-1,j=1,2,...,N

(6)

b(i,j)=a(i+1,j)·a*(i,j),

i=1,2,...,P-1,j=1,2,...,N

(7)

式(6)与式(7)进行相关运算可得：

(8)

3.2 载波频率估计

确定TDMA信号的突发起始位置之后，下一步对信号频偏进行粗估计和校正。本文采用数据辅助的方式，利用本地独特码消除接收信号中调制信息的影响，通过延迟共轭相乘的方法进行载波频率的快速粗估计。

图3 检测原理示意图Fig.3 Detection schematic diagram

将检测后信号中独特码对应序列r(i,j)同本地独特码进行双差分(延迟)共轭相乘得到

[r(i,j)·a*(i,j)]*,i=1,2,...,P

(9)

对Z求复角即可得到归一化的频率估计df

(10)

从式(9)和式(10)可以看出，利用独特码差分共轭运算估计频率的方法不存在相位折叠问题，频率估计范围为-1/2T～1/2T，可以满足实际信号中对大频偏的估计需求。

进一步地，考虑到式(9)差分使用的是延迟一个符号共轭相乘，而分布式独特码具有分段间隔插入的特点，可以增大差分间隔，采用延迟L0个符号共轭相乘，即相邻独特码段对应的符号共轭相乘的方式来提高频率估计精度。则式(9)和式(10)改写为：

[r(i,j)·a*(i,j)]*,i=1,2,...,P-1

(11)

(12)

由式(11)和式(12)可以看出，改进后的算法频率估计范围缩小为-1/2L0T～1/2L0T，而估计精度比之前提高了L0倍。

4 性能分析与仿真

为验证本文算法，在MATLAB环境下对仿真信号进行测试。设信号采样率Fs为800 kHz，符号速率Rs为200 KBaud，调制方式为QPSK。采样时间设为1000 ms，共有3个TDMA信号，每个信号突发时长为20 ms。

4.1 突发检测与帧同步性能分析和仿真

以延时一个符号共轭相乘的检测方法为例测试不同因素对检测算法性能的影响。假设信道环境为加性高斯白噪声，信噪比Es/N0={3 dB,6 dB,9 dB,12 dB}，独特码总长为48个符号，其中每个间隔插入2个符号的独特字。首先为验证频偏对算法检测效果的影响，分别对归一化频偏feT=0和feT=0.1的信号进行检测，取门限值th=0.70。仿真结果如图4和图5所示。

图4 feT=0情况下独特码检测算法得到的相关系数曲线Fig.4 The correlation coefficient curves obtained by the unique word detection algorithm in the case of feT=0

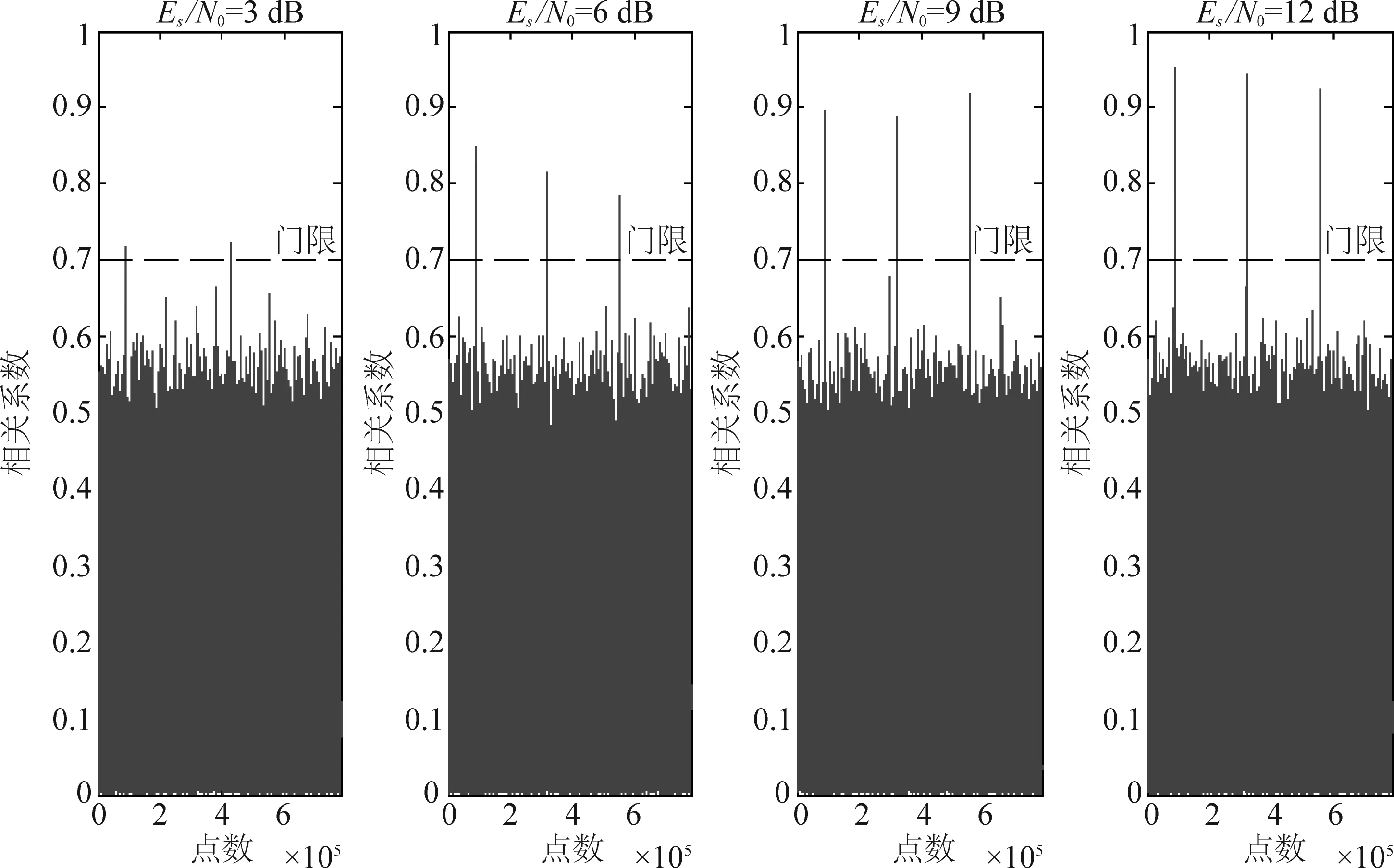
图5 feT=0.1情况下独特码检测算法得到的相关系数曲线Fig.5 The correlation coefficient curves obtained by the unique word detection algorithm in the case of feT=0.1

从图4和图5可以看出，在feT=0和feT=0.1两种情况下，算法检测效果差别不大，说明该算法具有良好的抗频偏性能，适合在较大频偏条件下使用。

忽略频偏影响的前提下，测试算法在不同信噪比下的检测性能，对算法进行蒙特卡洛仿真，统计虚警概率和漏检概率作为检测标准。实验结果如表1和表2所示。

实验过程中，在过采倍数Fs/Rs=4的情况下，实际匹配结果中通常有2～4个位置符合判为UW的条件，从中选取一个最佳位置(相关系数最大)判为UW准确位置即可。从表1和表2可以看出，相关系数门限(th)越大，则虚警概率越小、漏检概率越大；信噪比越高，则虚警概率越大、漏检概率越小。信噪比增高导致的虚警概率变大是因为当信噪比高时，(5)中Ar起到的作用就越大，信号数据与本地独特码相关系数就越大而导致虚警所占比例就越大。

表1 不同信噪比下检测的虚警概率

表2 不同信噪比下检测的漏检概率

图6所示仿真中独特码总长符号数分别为32、48、64、80，分布结构均为每段插入2个符号的独特码。可以看出，独特码越长，相关峰值越明显，检测效果越好。图7所示仿真中独特码总长固定为48个符号，分别采取每段插入2个、4个、8个和16个符号的分布结构。图示可见，两符号插入方式的检测效果最差，其他三种要明显好于第一种方式。

图6 不同独特码长下检测算法得到的相关系数曲线Fig.6 The correlation coefficient curves obtained by detection algorithm under different unique word length

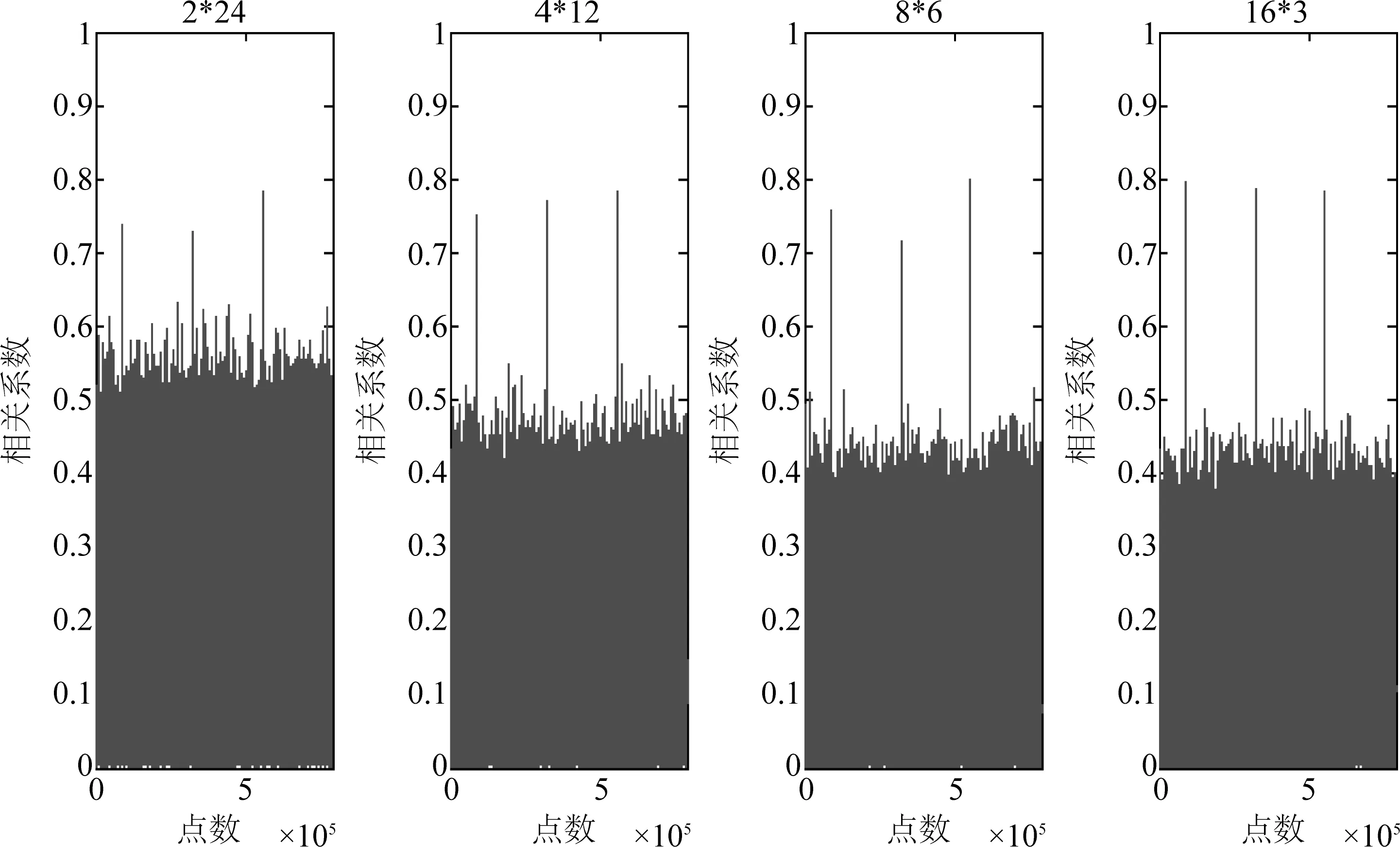
图7 不同独特码分布结构下检测算法得到的相关系数曲线Fig.7 The correlation coefficient curves obtained by detection algorithm under different unique word distribution structures

综合以上分析和仿真结果，对于延时一个符号共轭相乘的检测方法，信噪比越高、独特码越长、分段插入的符号数越多，越有利于提高算法的检测性能。

图8 两种检测方法得到的相关系数曲线Fig.8 The correlation coefficient curve obtained by two detection methods

图8所示仿真结果表明，对目前实际信号主要采用独特码每段2个符号插入的背景下，采取延时L0个符号共轭相乘的检测方法门限可以设置得更低，独特码匹配位置的相关系数越得到凸显，检测性能越好。在运算量上，每进行一次相关系数计算，对于延时一个符号共轭相乘的检测方法需要进行2(N-1)P次复数乘法运算和(N-1)P次复数加法运算，对于延时L0个符号共轭相乘的检测方法需要进行2N(P-1)次复数乘法运算和N(P-1)次复数加法运算，因此在独特码每段2个符号插入且独特码总长相同的情况下，延时L0个符号共轭相乘的检测方法比延时一个符号共轭相乘的检测方法复杂度更高一些。

图9 检测概率与信噪比关系曲线 Fig.9 Relation curve of detection probability and SNR

由于双滑动窗法是基于信号能量的检测，和信号编码结构无关，因此两种信号的双滑动窗法检测概率曲线基本一致。传统的集中式独特码可以看作是分布式独特码的一种特殊情况，由于其连续分布的特点，因此在采用本文共轭差分相关算法下，其参与相关运算的点数更多，相关效果更明显，因此其检测门限可以设置低些，在相同虚警概率Pf条件下其信号检测概率Pd要略高于分布式独特码信号。由图9可以看出，本文算法信号检测性能在低信噪比条件下要高于双滑动窗法，在相同检测概率下其信噪比门限比双滑动窗法降低2 dB左右。

4.2 频率估计性能分析和仿真

为验证算法的估计精度，对载波频偏feT=0.1的情况下，设置仿真条件信噪比Es/N0={3 dB,6 dB,9 dB,12 dB}，独特码长度为32、48、64个符号，每段插入2、4、8个符号独特码，相邻独特码段间隔L0=125个符号。分别对每种不同情况下进行5000次仿真，采用归一化频偏估计均方根误差(Root Mean Square Error,RMSE)δfT来衡量算法的频偏估计性能。

从表3的仿真结果可以看出，信噪比越高、独特码越长、分段插入的符号数越多，算法的估计精度越好。实验所得的频率的估计均方根误差均在3%符号速率以下，当信号质量较好时，误差往往控制在1%以内，基本能够满足大部分较大频偏估计校正的应用场景需要。

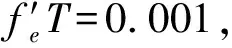
表3 频率估计仿真结果

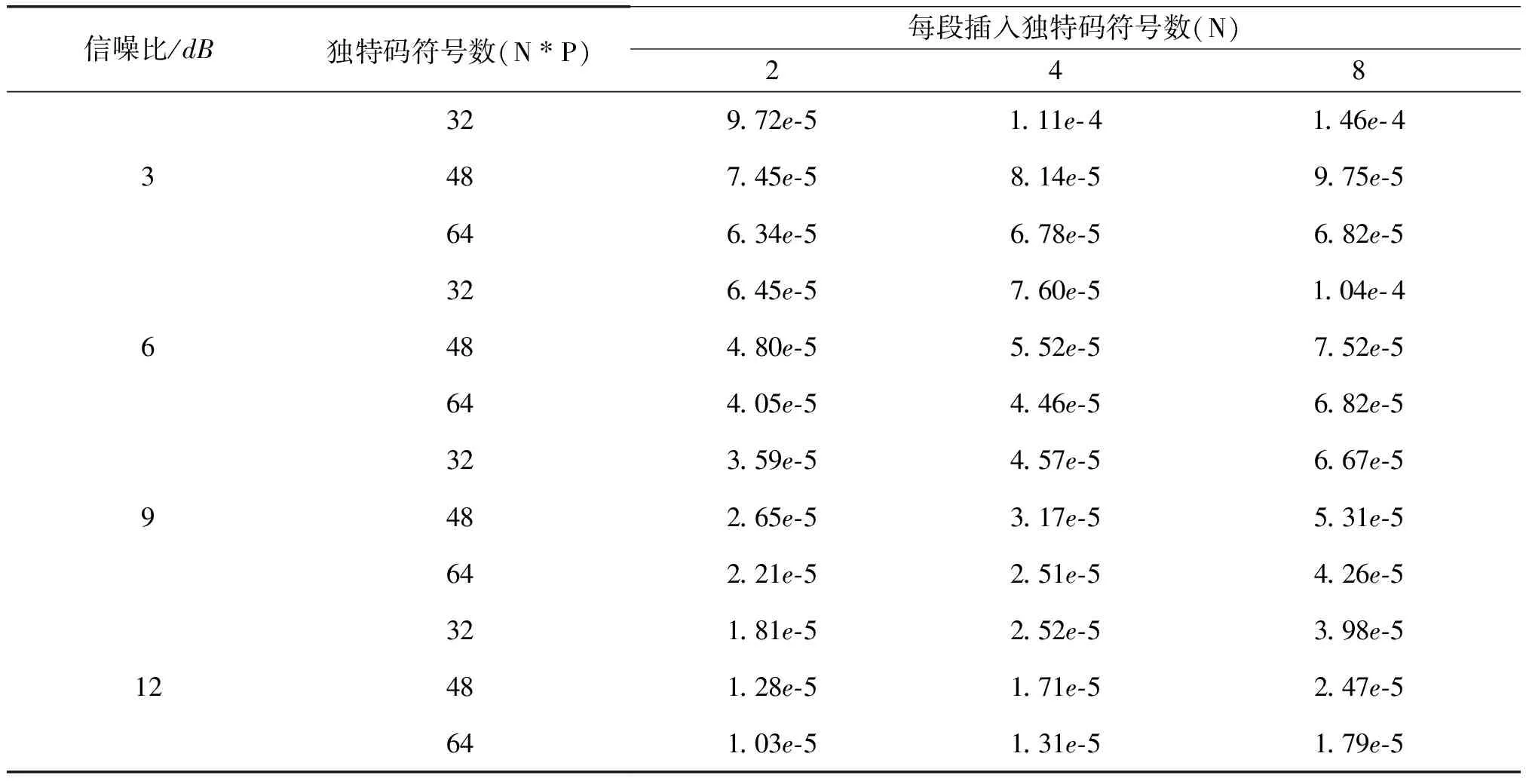
表4 采用延时L0符号频率估计算法仿真结果

5 结论

本文针对一类新型分布式独特码TDMA信号，提出了利用独特码进行突发检测和频率快速粗估计的算法，重点研究了信噪比、频偏、独特码长度和分布结构对算法性能的影响，并从目前主流的实际信号情况出发，对算法提出了具体的应用建议。仿真分析表明，检测算法具有良好的抗频偏性能和较高的估计精度，能够对较大频偏的TDMA信号进行精准定位；频率估计算法具有低复杂度、宽估计范围的优点，适合于较大频偏的快速粗估计。