大型数控机床床身应力分布检测方法研究
2018-07-26刘志松吴嘉锟
刘志松,吴嘉锟,况 康
(大连理工大学 精密与特种加工教育部重点实验室,辽宁 大连 116024)
0 引言
国产高档数控机床在服役过程中普遍暴露出精度保持性差的问题,已成为制约其竞争力的瓶颈。床身是数控机床的基础部件,其结构尺寸稳定性是影响机床整体性能和服役精度的关键[1]。在机床床身装配过程中,由于地脚螺栓间弹性相互作用等原因导致的床身装配应力不均匀,造成床身产生较大的局部应力,进而在机床服役过程中使床身产生大变形,进而使导轨滑块安装基准变化,加剧导轨滑块的磨损,降低机床的精度保持性[2]。因此,对机床床身的应力变化状态进行检测是对数控机床精度保持性进行合理评估的重要途径之一[3]。
国内外学者对床身的应力分布状态的检测做了系列研究。有限元数值模拟技术在床身铸造应力以及时效过程应力分布预测方面得到了广泛应用[4-5]。然而,在实际检测过程中,由于床身的尺寸大、结构复杂,极难完成对床身整体进行应力检测。盲孔法[6]等机械法检测由于操作繁杂,且破坏机床自身表面,因此目前仅用于研究层面,无法用于实践。对于X射线法[7]、中子衍射法[8]、超声法[9]、磁测法等无损检测方法,由于其对检测对象表面要求高,价格昂贵以及检测精度较低等特点导致无法在床身整体应力分布检测中应用[10]。
本文以大型/重型数控机床床身为对象,提出了基于分布式应变片的床身应力分布检测方法。该方法适用于预测床身装配后的应力分布。然后,以重型数控轧辊车床床身为研究对象,评估了应力分布预测算法,为指导床身低应力装配提供了理论基础。
1 基于分布式应变片床身应力分布预测方法
由于机床床身结构复杂,体积大的特点,对床身整体应力预测及其困难。虑及机床导轨安装基面应力分布会直接影响机床几何精度,其往往分布于床身的两侧。因此,需检测床身两侧面应力分布情况。此外,也需检测导轨安装面侧的应力分布情况。因此,将床身两个侧表面S1、S2及上表面S3的应力分布表征床身整体的应力分布情况,见图1。通过在三个表面粘贴应变片采集离散应变值,需通过应力分布预测算法实现表面应力场的拟合,完成应力的预测。

图1 等效平面分布与应力模拟
由上述分析,应力分布算法应遵循以下假设:①床身两个侧表面S1、S2及上表面S3的应力分布状态相互独立;②简化平面变形为弹性力学中的平面应变问题。由于提出算法需适用于任意测点布置形式。因此,以平面S1为例,阐述连续应力场拟合方法。
如图1所示,于床身侧表面S1建立直角坐标系,其中,X轴沿导轨方向,Z轴垂直于导轨方向,坐标原点可设定于除应变片粘贴处的任意位置。由弹性力学的平面应变问题可知,等效平面的应力场函数由应力函数φS1(z,y)决定,
(1)
式中,σxS1(x,z),σzS1(x,z)和τxzS1(x,z)分别为侧表面S1上正应力和剪应力场函数。假设S1上应力函数为多项式形式,则:
(2)

(3)

(4)

(5)
(6)
(7)
系数矩阵中,非零元素数N1及满足等效双调和方程的边界条件个数N2为:
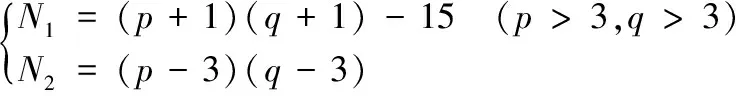
(8)
等效平面S1上粘贴的三向应变片个数为k,测得所有离散应变值个数为3k。因此,边界条件总数为N2+3k。由于系数矩阵中非零元素个数应与边界条件个数相同,即N1=N2+3k。因此,p与q应满足:
(9)
由于p与q为正整数,且x方向为误差非敏感方向,因此取q=4。则p为:
(10)

(11)
(12)
(13)
其中,由于p与q为整数,因此会产生冗余的边界条件。考虑多项式各项必须满足公式(5),且几何精度只与机床变形有关,而机床变形与正应力有关,因此多项式组则包含所有公式(11)、公式(12),而公式(13)则任选4k-2p-7=5个作为边界条件。
(14)
2 床身应力分布预测算法验证
以重型数控轧辊车床床身应力分布情况为检测对象,验证提出的床身应力分布算法,床身结构如图2所示。为了使床身产生应力,采用拧紧地脚螺栓改变床身变形的方法。

图2 重型数控轧辊车床与床身
鉴于目前对床身进行整体应力检测有较大的技术难度,因此采用数值模拟方法对提出的床身整体应力检测方法进行验证。由于该床身为典型的4导轨结构,具有体积大、结构复杂,非对称的特点。采用数值计算方法会产生巨大的运算量及耗费大量的时间。虑及提出床身应力整体检测方法适用于任意床身结构,因此仅检测床身一侧的单个导轨的应力分布情况。选择导轨表面及床身侧表面为两个检测平面S1、S2。于两个检测平面分别均匀粘贴8个应变片。粘贴应变片分布见图3。
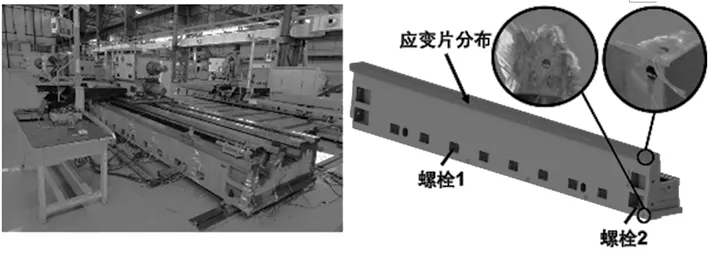
图3 应变片分布余螺栓编号
采用DH3816N静态应变测试分析系统对床身关键点处的离散应变数据进行实时采集。鉴于实验环境温度对测量影响较大,采用1/4桥(一片工作片、一片补偿片)的方法,粘贴于床身的应变片作为工作片,并在不受力、材料相同且温度相同的材料上接入相同应变片作为温度补偿片。
由于床身安装模拟场地原因限制,相邻地脚螺栓间隔为3000mm,地脚螺栓安装孔序号如图3所示。验证过程为:将床身放置到地基上,通过调整床身与地基间的垫铁,调节导轨面水平,然后依次采用力矩扳手向地脚螺栓1,地脚螺栓2施加60kN的预紧力。为使床身充分变形,每预紧一个螺栓使床身静置3h,并连续采集10次各测点的应变值并取平均值以消除随机误差。并以采集应变值作为边界条件按提出算法计算导轨变形量。
为验证提出算法,采用有限元分析软件Ansys建立床身有限元模型,模拟螺栓依次预紧后床身导轨应变分布情况。为减小运算量,优化运算时间,对被检测导轨进行网格细化处理,网格共有332945个。建立有限元模型如图4所示。

图4 床身有限元模型
其中,地基与垫铁、垫铁与床身的接触为摩擦约束,摩擦系数为0.15,地基底部为固定约束。为迫使床身产生应力,依次向螺栓1与螺栓2施加预紧力60kN,数值模拟导轨两个等效平面应力分布与采用算法计算结果如图5所示。
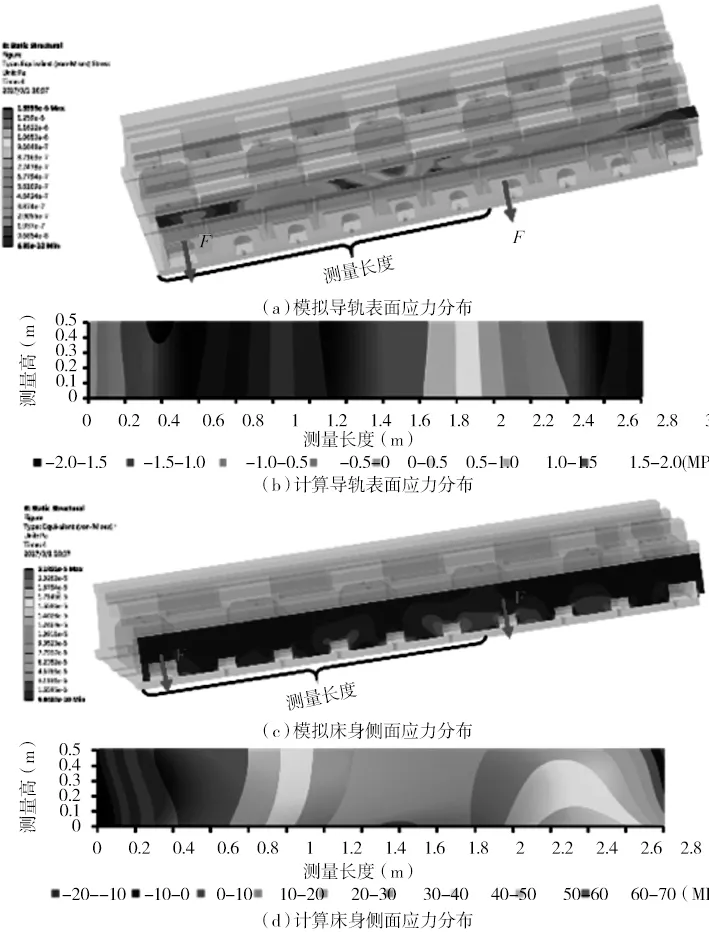
图5 床身应力分布
图5a、图5c分别为螺栓预紧后床身应力分布的数值计算结果。图5b、图5d为通过应力分布预测算法计算出的床身应力分布结果。对比发现,所得应力分布结果有较好的一致性。提出的预测算法可较好的反映出床身应力分布情况,即在预紧部位的应力变化较大,如图5d所示。然而,提出的算法并不能精确反映出最大应力分布的精确位置,这是由于在预紧部位并没有粘贴应变片,缺少必要的边界条件。此外,在床身侧面的预测应力分布的边缘以及在床身导轨表面靠近边缘处出现了负应力。这是由于在实应力分布情况中,当被检测件局部产生了较大的应力,周围应力会迅速衰减至0,而多项式拟合应力分布的则不能有效的表征这种现象,会产生应力波动。因此,该多项式拟合方法只适用于没有局部大应力集中现象出现的情况。
3 总结
大型数控机床床身应力分布的检测是评估机床精度保持能力的重要问题。本文结合平面问题的应变理论,提出了基于分布式应变片的数控机床床身应力分布检测算法。以重型数控轧辊车床的床身为对象,采用提出方法,预测其床身应力分布状态,并用有限元方法对该方法进行了验证。结果表明,该方法能较好的预测出床身应力分布情况。
