基于平顺性和操稳的某重型越野车悬架参数优化

居刚，王凯峰，陈兴华

（安徽江淮汽车集团股份有限公司，安徽 合肥 230601）

前言

悬架是汽车上的重要组成部件，其性能的优劣直接影响着汽车的平顺性与操纵稳定性，悬架应具有良好的运动学特性，在其轮跳中应保证轮跳定位参数在合理的范围内变动，从而改善汽车的操纵稳定性和转向轻便性、减少轮胎的磨损等[1]。本文通过悬架模型的建立，并对悬架进行分析，再得到各种性能曲线，选取不合理的性能参数作为优化目标，并对设计参数进行优化，以改善悬架系统性能，提高设计效率。

1 模型建立

整车多体动力学模型的建立是在整车三维模型的基础上建立的参数化模型，其不仅反映了整车及各部件的外形尺寸和质量特征，还输入了弹簧、阻尼器和衬套等所属的力学参数，能够很好地还原整车的真实特性，所以在对整车多体动力学模型的仿真更接近整车试验水平。

本文所研究的是一款带平衡轴悬架的 8X8重型战术车辆，其第一轴和第二轴分别采用的是带钢板弹簧的非独立悬架，第三轴和第四轴共同采用一等臂式平衡轴悬架，第一轴和第二轴悬架采用少片式钢板弹簧，平衡轴悬架用一根反向安装的少片式钢板弹簧作为弹性元件，每一轴上均采用双向筒式液压减振器作为阻尼元件且安装限位块。

整车建模具体的步骤：

（1）将整车分解成若干个子系统，本文所研究的车型分别如下：第一轴悬架子系统、第二轴悬架子系统、平衡轴悬架子系统、前钢板弹簧子系统、后钢板弹簧子系统、动力总成子系统、车身子系统、转向系统子系统和轮胎子系统。并分清各个子系统之间的相互连接关系，为下面的通讯器的建立做准备。

（2）在Template Builder中，建立各个子系统相对应的模板，先从结构形式上建模，由几何参数对各个零部件建立模型，再由质量参数和力学特性参数修改各个零部件的质量、转动惯量以及属性文件等，并建立用以连接的通讯器。

（3）在上一步的基础上，对建立好的的模板建立相对应的子系统模型。

（4）将上述已经建立好的子系统在Standard Interface中装配成整车多体动力学模型。

整车建模的拓扑关系图如图1所示：

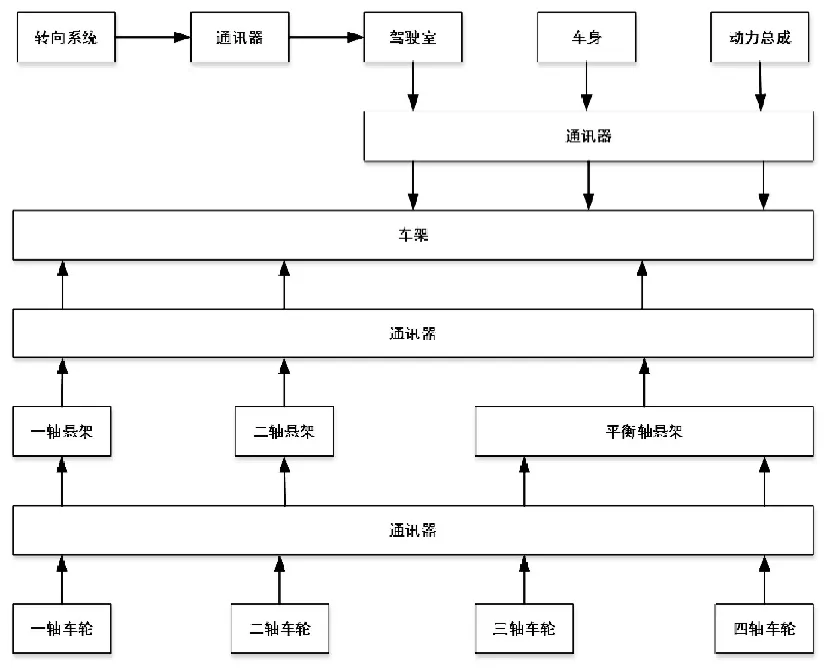
图1 整车建模的拓扑关系图

2 平顺性参数的优化与分析

2.1 优化变量与目标的确定

为了进一步改善车辆轮胎侧磨状况，对悬架参数进行进一步优化。优化设计中选择车轮前束角、车轮外倾角在仿真过程中的最大绝对值作为优化目标，使优化目标的变动范围尽可能缩小[2]。选择板簧前卷耳点，吊耳点，横向拉杆端点三个硬点的九个坐标值作为优化的变量，硬点的坐标变化范围设定为[-10,10]mm[3]。

2.2 灵敏度分析

利用Adams/Insight进行试验设计，试验策略采用二水平试验设计筛分法，使用这种方法对九个设计变量进行筛选，选取其中影响度较大的设计变量，采用全因子设计方法[4]。

运行试验后，对仿真结果进行拟合。R2和R2adj表示拟合的好坏程度，当R2在0～1之间，越大越好，且理想的拟合状态是大于0.9；R2adj 通常小于R2，R2adj 的值为 1 时表明拟合得非常好；P是指拟合表达式中是否含有有用项，拟合表达式中的有用项个数随着P值的减小而增多；R/V是指模型计算值和原始数据点之间的关系，其值越高，表明预测结果越好，当R/V值高于10时，预测结果非常理想；当 R/V值低于4时，预测的结果非常不理想[5]。通过拟合良好程度（Goodness-of-fit）项检查拟合得好坏，其各值见图2，从表中可以看出拟合得比较理想。

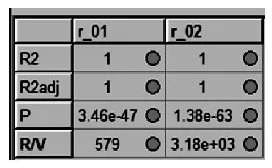
图2 仿真拟合图

导出分析结果，从中可以看出各因素对应的影响度，对前束角影响度较大的变量如图3，图4所示。

图3 分析结果图

图4 分析结果图

从图3可以看出在第一轴中前卷耳点的x坐标对前束角的影响度超过10%，需对其进行优化。图4可以看出第二轴中前卷耳点的x,z坐标对前束角的影响度超过了10%，因此需要调整这两个坐标对第二轴进行优化。

2.3 优化前后仿真分析结果对比

根据灵敏度分析，对影响较大的两个坐标在相对范围[-10,10]内进行调整，优化前后的结果对比图如下。

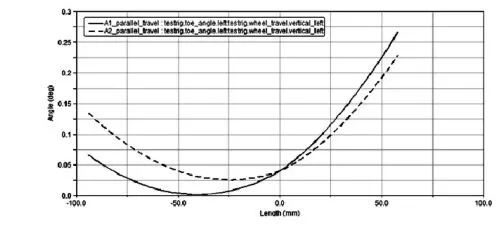
图5 第一轴前束角优化前后对比

图6 第一轴优化前后主销 后倾角对比

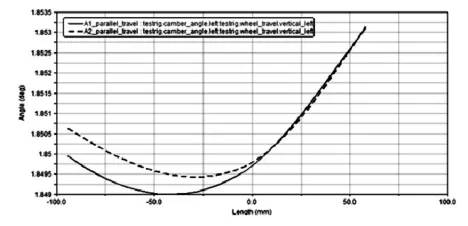
图7 第一轴优化前后外倾角对比

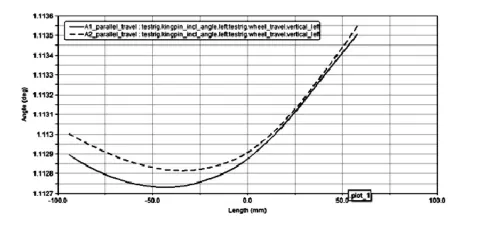
图8 第一轴优化前后主销 内倾角对比

图9 第一轴优化前后轮距变动对比

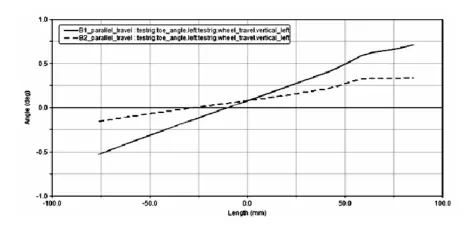
图10 第二轴优化前后 前束角对比

图12 第二轴优化前后 外倾角对比

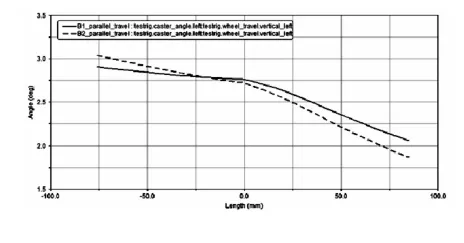
图11 第二轴优化前后主销后倾角对比

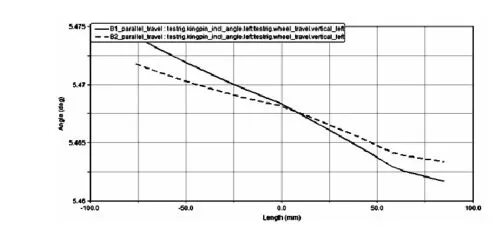
图13 第二轴优化前后主销内倾角对比

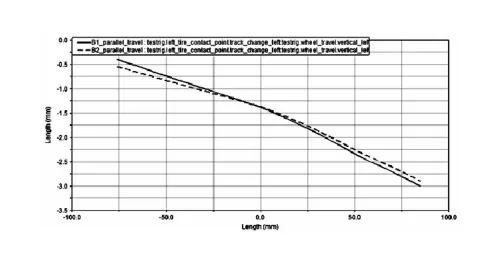
图14 第二轴优化前后轮 距变化对比

由前后对比分析图可以看出，优化过后轮跳过程中，前束角、主销内倾角，外倾角，轮距变动的变化范围都不同程度减小，达到了预期的目标，主销后倾角的变化范围有一定程度的增大，这是优化前束角和外倾角的过程中所不可避免的，增大的程度完全是可以接受的。

3 转向回正性参数的优化与验证

3.1 参数的选取

根据上述对影响重型战术车辆操纵稳定性因素的分析，其中残余横摆角速度与主销后倾角和主销内倾角成反相关，但受板簧刚度的变化的影响很小。而侧倾角受主销内倾角和主销后倾角的影响很小，当板簧刚度降低时，侧倾角也会随之减小，但减小幅度很小，故不对板簧刚度做调整。由分析结果确定一组更优的悬架参数，一二桥的主销内倾角取7.8°，主销后倾角取 4°。参数优化前后的硬点坐标和板簧参数如表1和表2所示。

表1 一桥优化前后的硬点坐标和参数对比

表2 二桥优化前后的硬点坐标和参数对比

3.2 优化参数的验证

把优化后的参数带入整车仿真模型中进行操纵稳定性仿真验证，与优化前的仿真结果进行对比。

3.2.1 整车稳态回转试验仿真分析

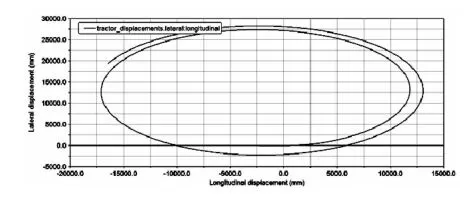
图15 整车稳态回转仿真轨迹

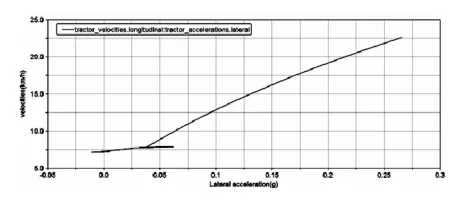
图16 纵向车速VS侧向加速度

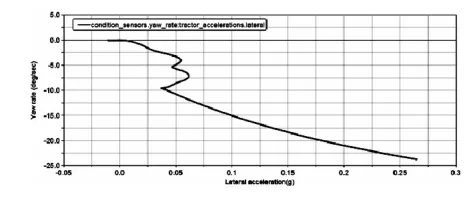
图17 横摆角速度VS侧向加速度

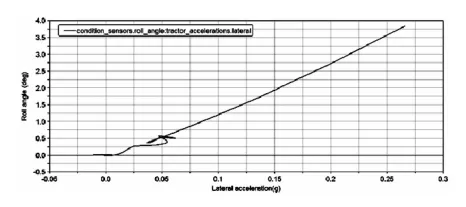
图18 侧倾角VS侧向加速度

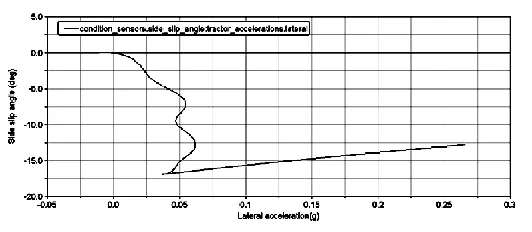
图19 侧偏角VS侧向加速度

把优化后的参数带入整车仿真模型进行稳态回转试验，使汽车以最低稳定速度沿半径为 15m的圆周行驶，待稳定后，缓缓连续而均匀地加速（纵向加速度不超过0.25m/s2），直至汽车的侧向加速度达到6.5m/s2（或受发动机功率限制而所能达到的最大侧向加速度、或汽车出现不稳定状态）为止，记录整个过程。

对上述数据进行处理得到转弯半径比的仿真结果和前后侧偏角的仿真结果如图20和图21。

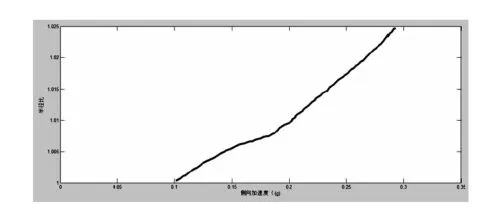
图20 半径比VS侧向加速度

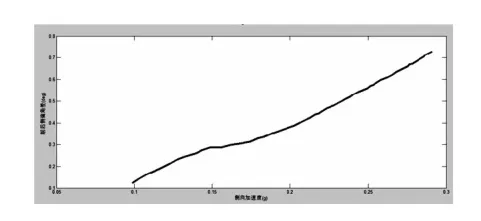
图21 前后侧偏角VS侧向加速度

依据QC/T 480汽车操纵稳定性指标限值与评价方法，对整车稳态回转性能的评价计分如表3。

表3 稳态回转性能评分

3.2.2 转向回正试验仿真分析

转向回正试验用于确定车辆的转向回正力，评价汽车由曲线自行恢复到直线行驶的能力。低速回正试验是使汽车沿半径为15±1m的圆周行驶，调整车速，使侧向加速度达到0.4g,固定转向盘转角，稳定车速并开始记录，待3s后，驾驶员突然松开转向盘，记录松手后4s的汽车运动过程。

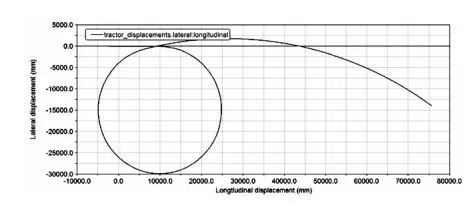
图22 低速回正仿真行驶轨迹

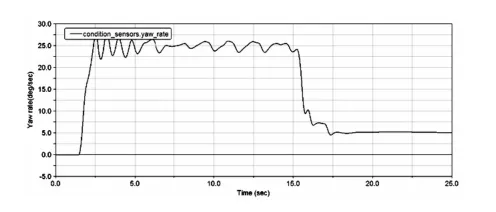
图23 横摆角速度响应

图24 方向盘转角输入曲线

表4 转向回正性能评分

依据QC/T 480汽车操纵稳定性指标

限值与评价方法，对整车转向回正性能的评价计分如表4所示。

3.3 分析评价

根据上述的评分结果可以看出，相对于优化前的指标评分，优化后的模型在稳态回转性能上基本没有区别，分值不相上下，在转向回正性能上，仿真后该车辆的残余横摆角速度由6.32 deg/s减小到5.09 deg/s，转向回正的评分也由优化前的66.9增加为优化后的77.7，表明该车辆的操纵稳定性在优化后得到了较为明显的改善。

4 结论

本文通过建立某重型越野车平顺性和操纵稳定性的模拟仿真分析模型，并基于各自评价指标进行分析计算，建立起该重型越野车的优化设计模型和优化目标，通过对悬架系统刚度值和阻尼值的优化分析计算，得出新的优化参数，结果表明车辆的平顺性和操纵稳定性均得到了较好的改善，仿真模型对悬架系统关键性能的优化起到重要指导作用。