从三角函数上渗透数学思想方法培养数学核心素养

湖南省永州市一中 白 炜

在三角函数这一章的学习和小结中，熟练掌握以下几种数学思想方法，有助于提高学生灵活处理问题和解决问题的能力，也是培养学生数学核心素养的途径之一。下面通过例题透视三角函数中的数学思想方法。

一、数形结合思想

“数无形，少直观，形无数，难入微”，利用“数形结合”可使要研究的问题化难为易、化繁为简。我们不可能把“数”和“形”完全孤立地割裂开，也就是说，代数问题可以几何化，几何问题也可以代数化，“数”和“形 ”在一定条件下可以相互转化、相互渗透。解析：将已知函数式看成单位圆上的点2）连线的斜率，如图所示，观测得

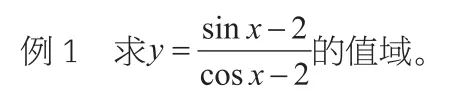
小结：利用单位圆中三角函数线或正弦曲线、余弦曲线、正切曲线求解某些三角等式或不等式问题或取值范围；运用数形结合的思想化抽象为直观，使问题简单明了，数形结合在三角中有着广泛的应用。

二、分类讨论思想

当一个问题因为某种量的情况不同而有可能引起问题的结果不同时，需要对这个量的各种情况进行分类讨论。分类讨论是数学解题的重要手段，如果对学过的知识恰当地进行分类，就可以使大量纷繁的知识具有条理性。

小结：由于函数 的最大值（或最小值）取决于系数A的符号，所以像这种含参数的问题要进行分类讨论。

三、转化与化归思想

转化与化归是指同一命题的等价形式。可以通过变换问题的条件和结论，或通过适当代换转化问题的形式，或利用互为逆否命题的等价化归来实现。

小结：处理数学问题的实质就是实现新问题向旧问题的转化、复杂问题向简单问题的转化、未知问题向已知问题的转化、抽象问题向具体问题的转化等。在计算、化简和证明三角函数时，常采用化繁为简、化异为同、化切为弦、“1”的代换、整体代换等方法，这些都体现了三角函数问题中转化与化归的思想。