波利亚的“解题表”在数学应用题教学中的应用

江苏省淮安经济技术开发区徐杨中学 盛 杰

波利亚认为：教育就是应“教会年轻人去思考”，就是应培养学生的“独立性、能动性和创新精神”,教师那种照本宣科式地讲述和教科书上那种突如其来的 “像是帽子里跑出一只兔子”式的证明，实在令人不满,教学生解题是“意志的教育”，当学生求解那些对他来说并不太容易的题目时，他学会了等待灵感的到来，学会了当灵感出现后全力以赴。如果学生在学校里没有机会尝尽为求解而奋斗的喜怒哀乐，那么他的数学教育就在最重要的地方失败了。

一、审题

审题就是弄清题意，审题是解题过程的首要步骤。审题是否正确，直接影响到解题的成败，审题能力的高低直接反映了学生的解题能力和数学学习的水平。正确审题很重要，一审条件，二审结论。审查题设条件要全面，能分清主次，对已知条件既不遗漏，也不随意外加，还要特别注意细节或者隐含的条件。

例题：如图，小红想知道旗杆的高度，将升旗的绳子拉到旗杆底端，她发现还多1米，然后将绳子末端拉到距离旗杆8米处，发现此时绳子末端距离地面1米，请你帮小红求出旗杆的高度（滑轮上方的忽略不计）。

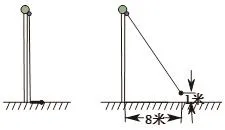
本题是中档题，难度不大，由于审题不清把绳子末端距离地面的垂直距离看成是拉下来的长度，导致做错，学生知道了用勾股定理求解绳子长度，但因为审题不清而求解错误实在可惜。

抓好“审读功”，做到泛精结合。数学解题最重要的一关就是审题阅读能力，要做到泛读与精读有机结合，确保试题信息输入大脑是正确的、全面的。难题难在理解题意。首先要引导学生先泛读，了解大概题意，知道已知条件，解题目标等；其次就是精读，字斟句酌，反复推敲，进行三种数学语言的转化，争取把握住题目的本质、考查的主要知识点、命题者的真实意图等。很多学生的致命缺点就是审读题目不细致，粗枝大叶，想当然地定式思维。

二、探索

通过审题弄清条件结论之后，接下来进入求解探索过程，就是寻求结论和条件的联系，打通条件结论的逻辑联系，从而找出等量关系，相等关系是什么？哪些是通过关键词语明显给出的？哪些是条件之间的关系隐蔽限定的？哪些是由数学公式、物理定律提供的？哪些是变动中的不变量或不变性质所暗示的？列个表，画张图。这是解答应用题的钥匙，它需要回顾条件与结论中涉及哪些概念，与哪些定理、公式、法则有关，需要用到哪些基本技能，方法是什么等等。因为解题思路来源于数学基本概念知识、基本技能。

例题：A、B两地间的路程为18千米，甲从A地、乙从B地同时出发相向而行。二人相遇后，甲再走2小时30分到达B地，乙再走1小时36分到达A地，求二人的速度。

讲解：设甲的速度为x千米/小时，乙的速度为y千米/小时。题目的基本关系是：路程=速度×时间。

相遇时，甲、乙各走了小时（相向而行在相遇处各走的时间是不变关系）。

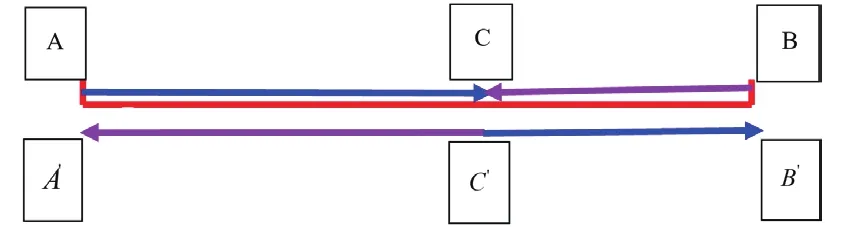
（1）甲、乙所走的时间相等。

（2）甲、乙所走的路程之和等于全程。

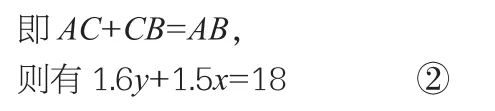
相等关系2：由甲、乙的路程共同提供。

（3）甲在相遇后走的路程=乙在相遇前走的路程。

即C'B'=BC，

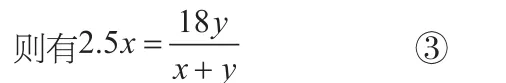
（4）乙在相遇后走的路程=甲在相遇前走的路程。

即C'A'=AC，

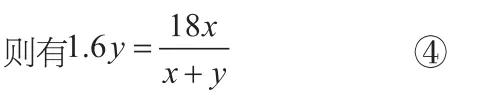
相等关系3：分别由甲、乙路程提供。

（5）甲在相遇前的路程+甲在相遇后的路程=全程。

即AC+C'B'=AB，

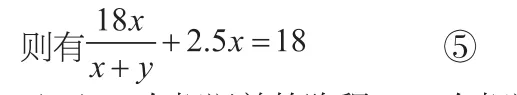
（6）乙在相遇前的路程+乙在相遇后的路程=全程。

即BC+C'A'=AB，

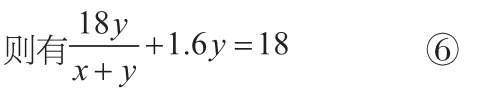
相等关系4：分别由甲、乙的时间提供。

（7）甲在相遇前走的时间+2.5=甲走全程时间。

（8）乙在相遇前走的时间+1.6=乙走全程时间。

这样，从路程、时间、速度及其关系中已经找到了8个等式（并不独立），有了这么多的方程，本题也就迎刃而解。

三、解答

解答是指把答案正确严谨地表述出来，解题过程要求理由充分、叙述正确、符合逻辑、条理清楚、作图正确。简洁而又准确的叙述不仅是解题的要求，甚至影响解题的成功，这实际上体现了较高的数学思维能力，因此，笔者在解题教学过程中特别注重正确简洁的解答示范，规范解题过程，逐步培养学生严谨的表达能力和运算能力。

四、反思

一道题目完成了并不是解题的结束，解题后要注重反思。反思是提高解题能力的一个重要途径，是总结解题思想、方法、规律、技巧、策略的重要方式。反思数学问题的本质，反思解题的审题、探索过程，思考概念、知识、技能是如何应用的，总结解题技巧方法，起到举一反三、触类旁通的作用。

学生通过对应用题“解题表”的应用，锻炼了学生的逻辑思维能力、分析问题和解决问题的能力，通过对应用题的教学，培养学生分析问题和解决问题的能力。由于应用题贯穿中学数学教学的始终，从这个角度看，把解应用题的基础打好，对学好整个中学数学是大有益处的。