探讨一道疑似错题的额外价值

伍秀峰

(上海市位育中学 上海 200231)

1 引言

作为物理学科，要求的是理性分析现象和规律，但仅仅是定性处理显然是不够的，它与自然课的很大区别在于理解现有的规律和公式，并运用到判断和计算方面.测量和计算是研究中不可或缺的环节，这方面的练习题能够起到培养学生科学素养的目的；虽然物理是建立在实验的基础上的，但真实世界非常复杂，需要将其简化为物理模型才能让学生去处理，由此在出题时常常会编造数据及条件，甚至在实验题中也会有凑数字的现象，那么如果给的是真实数据，但不同的观点得出矛盾的结果，又该如何看待？

2 题干暗含的矛盾

【题目】(2013年普通高等学校招生全国统一考试海南卷)某同学用图1所示的实验装置验证机械能守恒定律.已知打点计时器所用电源的频率为50 Hz，当地重力加速度g=9.80 m/s2.实验中该同学得到一条点迹清晰的完整纸带.纸带上的第一个点记为O，另选连续的3个点A,B,C进行测量，图1中给出了这3个点到O点的距离hA,hB和hC的值.回答下列问题(计算结果保留3位有效数字).

(1)打点计时器打B点时，重物速度的大小vB=______m/s;

(2)通过分析该同学测量的实验数据，他的实验结果是否验证了机械能守恒定律？简要说明分析的依据.

图1 验证机械能守恒定律装置示意图

显然可根据A到C的平均速度作为中间时刻的瞬时速度求出vB=3.90 m/s，这里不再研究第2问，转而研究实验中体现的加速度.根据v2=2gh，及hB=0.785 7 m，可得g=9.68 m/s2，显然比理论值小的原因可以解释为阻力的影响，不算太严重.但从另一个观点求得的加速度出了问题：在此匀变速运动中应当满足hBC-hAB=gt2，其中t=0.02 s，以此逐差法求得g=11 m/s2.两种计算上应该都没问题，但是结果矛盾，参考文献[1]认为由这道题的相关数据既然可以算出如此不合理的加速度，所以是出错了题.虽然文献[1]用的是另一道数字不同的题干，但可见这种情况普遍存在，亟待合理的解释.

3 逐差法的认识

如果存在4段已知长度hAB,hBC,hCD,hDE，就可以求重力加速度的平均值，利用hCD-hAB=2gt2和hDE-hBC=2gt2分别求出g后相加除以2.为什么不是相邻的两段相减求出3个g值取平均呢？因为你会发现这样相加后消掉了hBC,hCD的数据，误差更大的原因是使用的数据更少.对于海南卷中的这道题，用逐差法求加速度，方法正确但所用的数据范围过小(A至C之间)也会导致大的误差存在，不妨就从测量误差来估计一下：根据刻度尺的最小分度，我们可以估计每个长度测量值的误差大小在0～0.000 2 m，而求g的表达式为

用到了4次测量值，估计分子的不确定度在0.000 8 m范围内，但观察分母为0.022，相当于将此误差放大到2 500倍，所以g值的误差大小估计在0～2之间，那么得到那样的数据就可以理解了.相比之下，v2=2gh的观点则是用上了足够大范围的数据(从起点开始的位移)，应该更具有说服力.

4 全位移算法的误差估计

即

5 图像的观点

vA=vB-gtvC=vB+gt

代入数据得

vA=3.704 m/svC=4.096 m/s

分别平方作为纵坐标，再以3个点的下落高度h为横坐标作出了图2所示的直线拟合(Origin软件)，可见毕竟存在误差，直线是不过原点的，而下方的直线方程表达式y=A+Bx里，斜率B即为2g，可算得

g=9.799 7 m/s2

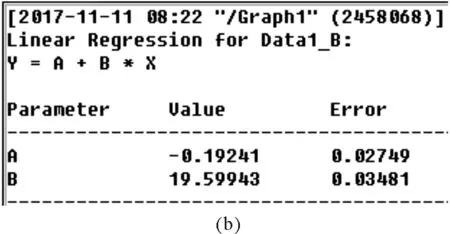
图2 v2-h直线拟合图像及相关的数据

这当然跟我们用9.8 m/s2的加速度去反推在A，C点的速度有关，所以第2次用计算值g=9.68 m/s2,求得

vA=3.706 4 m/s

vC=4.093 6 m/s

再次作图(图未显示)后得到新的直线方程表达式如图3所示，算得

g=9.679 69 m/s2

虽然这个值基本上也是默认加速度为9.68 m/s2而得到的，但仔细观察这两个直线方程的截距，第2次的-0.004 08 m2/s2极小，明显更加过原点了，说明加速度为9.68 m/s2是可信的，因为一般保持在O点速度为零并非难事.

图3 第2次作图后得到的数据

再仔细思考一下，这两次直线的截距都是负值，显然不能对应任何O点的初速度，应该是源于那几个测量数据的误差；负的截距会导致偏大的斜率，说明这几个数据点本身就可能会造成加速度测量值比真实值(或者说是均值)偏大，而如果这个误差再集中在小尺度范围内被放大(一次逐差的计算)，是否在一定程度上支持了那个g=11 m/s2的出现呢？但是与文献[1]中一样,逐差计算值都不是偏小而是偏大很多，深层原因还有待广大同仁进一步研究.

6 总结

实验是不容作假的，通常出题也会尊重事实；打点计时器的内容我们研究的很多，用来求重力加速度其精度还可以接受，通常编成习题时没必要在数字上再进行处理.逐差、全程、作图都是正确的求重力加速度的观点，只是偶然误差在小范围的数据中体现得更加明显一些，由此即认为题目出错是值得商榷的.虽然这里的推导也很不严密，但从多个角度去理解实验事实，不失为一种科学的研究手段.