一种弹性折叠压电悬臂梁的结构设计及发电特性研究

2018-07-25，，

机械与电子 2018年7期

，，

(中国科学技术大学精密机械与精密仪器系，安徽合肥 230026)

0 引言

近年来，随着无线传感器和MEMS技术的迅猛发展，这些装置的自供电技术受到广泛关注。由于环境中的振动无处不在，若能利用振动发电，无疑是一种经济方便、极具潜力的供电方式。通过压电材料可以将环境中的振动能量转化成电能，十分符合这一需求。目前提出的压电结构，其一阶共振频振频率更是高达几百赫兹。然而环境中的振动大多分布在250 Hz以下[1- 2]，上述结构远远不能满足现实条件下的低频宽带振动发电要求。

为了拓宽振动发电的有效频响范围，国内外学者提出了许多方法，如压电阵列[3- 4]、非线性双稳结构[5- 7]、多模态系统[8- 12]等。对于压电阵列来说，整体结构复杂且体积增大，单位体积发电量并未增加。对于非线性双稳结构来说，可以实现一阶共振频率周围的振动发电，频率大多在百赫兹以上，二阶共振不具有回收高阶模态的振动能力。对于多模态系统来说，可以通过巧妙设计结构使得第二阶振动频率得以利用，例如Abdelkefi[8]构造了一种弯扭耦合结构，通过不对称的末端质量引起弯扭振动，且当不对称性增加时，前两阶共振频率会变得更加接近；Wu[9]构造了一种主—内悬臂梁的两自由度结构，与传统的单自由度悬臂梁相比具有更好的振动频响特性。可见多模态系统在利用高阶振动模态进行振动发电方面有一定优势。

本文构造了一种以3D打印材料PLA为基体的弹性折叠压电悬臂梁结构。相较于多自由度系统，该模型结构简单，避免了复杂的设计，且前两阶模态均可在50 Hz以内激发出来，可有效拓宽振动发电频响范围。和传统压电悬臂梁相比，其振动发电频率降低，效率也有显著提高。

1 结构及其振动特性分析

1.1 新型弹性折叠压电悬臂梁结构

新型弹性折叠压电悬臂梁结构由弹性折叠梁和质量块组成，如图1a所示。相较于传统悬臂梁，折叠梁可以显著降低结构刚度，进而降低共振频率，使得该结构能够在低频范围内回收振动能量。在悬臂梁底部贴有压电片，用以将振动能量转化成电能。折叠压电悬臂梁仿真模型结构如图1b所示。

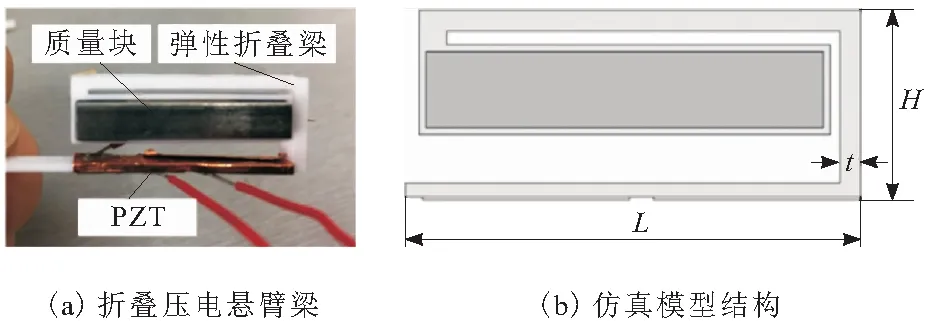
图1 折叠压电梁结构

1.2 振动特性

首先用有限元分析软件COMSOL对该结构的振动特性进行了分析。仿真时的结构参数如下：梁长L=30 mm，宽W=5 mm，高H=15 mm，厚度t=1 mm；质量块嵌入框中。弹性梁选用PLA，弹性模量E0=3.8 GPa，泊松比μ=0.46，密度ρ=1 250 kg/m3。质量块为结构钢，弹性模量Es=200 GPa，泊松比μs=0.33，密度ρs=7 850 kg/m3。PZT选用PZT- 4，压电材料常数d31=-123 pC/N，e33=663.2，s11=12.3×10-12m2/N, 密度ρp=7 500 kg/m3。将弹性梁的左端作为固定端，仿真计算其振型。如图2a和图2b所示，该结构前两阶振型为M1和M2，共振频率分别为22.4 Hz和39.8 Hz。

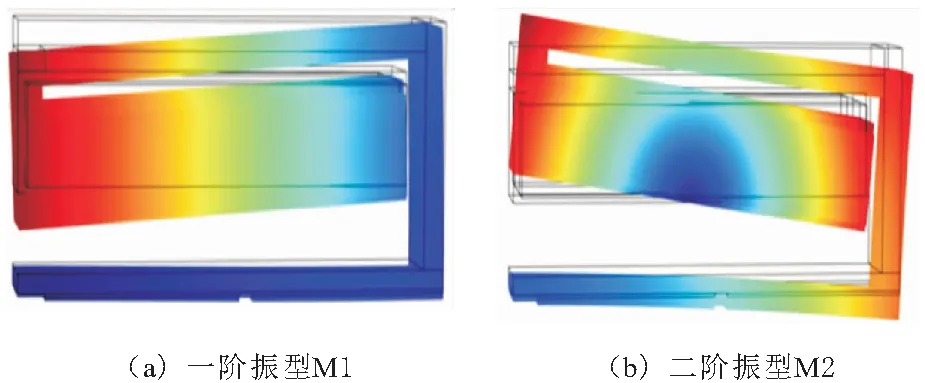
图2 折叠压电梁前两阶振型

压电片中性层的应力分布如图3a和图3b所示。对于第一阶振型M1，梁两端的拉压应力达到最大，利用压电片可以有效地将振动能量转化成电能。对于第二阶振型M2，其应力曲线几乎水平，表明应力沿梁长分布均衡，因此也能在该频率处产生较大的电能输出。前两阶共振频率间隔仅为17 Hz，十分接近，即该模型可以在低频范围内实现多模态的振动，进而通过压电片实现多个峰值的振动发电效果。

图3 前两阶共振频率下压电片中性层应力分布

1.3 模型参数对共振频率的影响

图4 模型参数对前两阶共振频率的影响

2 实验模型的制作及测试系统的搭建

2.1 实验模型的制作

利用3D打印机打印出折叠梁，3D打印材料为PLA。在梁的底部下表面用金属箔引出一个电极，再在金属箔上用环氧胶粘剂(DP460，3M，Inc)贴上压电片，压电片的下表面作为另外一个电极。压电片的极化方向为厚度方向。折叠梁的上端打印出一个框，便于质量块放入。还打印出了夹具和底座，便于将模型固定在振动台上。为了验证模型的可靠性以及互补性，通过参数设计制作出共振频率不同的2个模型，并且制作了带有末端质量的传统压电梁用于对照实验。

2.2 测试系统的搭建

测试系统如图5所示，包含电磁式振动器(K2075E040, modal Shop, Inc.)，功率放大器(2100E21, Modal Shop, Inc.)，信号发生器(DG1022, RIGOL, Inc.)，示波器(DPO2012,TEK,Inc.)，压电式加速度计(B&K 4371)和能量回收电路。模型通过夹具固定在底座上，一端夹紧，另一端自由振动，底座固定在振动器上。通过信号发生器产生1～100 Hz的正弦扫频信号，扫频步长1 Hz，扫频时长10 s。扫频信号由功率放大器放大后传入振动器，作为模型的输入激励。加速度计固定在底座上，用来测量振动加速度。模型通过底部的压电片将振动能量转化为电能，经过能量回收电路进行回收。利用示波器测量电压信号和加速度信号，并通过示波器自带的软件来采集实验数据。

图5 测试系统

3 实验结果及分析

分别测量了模型的电压信号和加速度信号，并将实验采集得到的信号数据进行FFT变换，分别得到V(ω)和A(ω)，再通过公式计算得到归一化加速度(即单位加速度)下的输出电压频响。

Vn=|V(ω)/A(ω)|

(1)

Vn为归一化电压；V(ω)和A(ω)分别为电压信号和加速度信号经傅里叶变换所得。模型1、模型2和传统压电悬臂梁的开路电压频响如图6所示，其中传统压电悬臂梁在50 Hz内只有1个电压峰值(31.8 V/g，33.1 Hz)，而模型1、模型2各有2个电压峰值：模型1为M1(43.9 V/g，22.4 Hz)和M2(23.8 V/g，39.8 Hz)，模型2为N1(32.6 V/g，27.6 Hz)和N2(33.7 V/g，43.7 Hz)，且峰值均高于传统压电悬臂梁，实现了振动发电频率的降低、效率的提高。

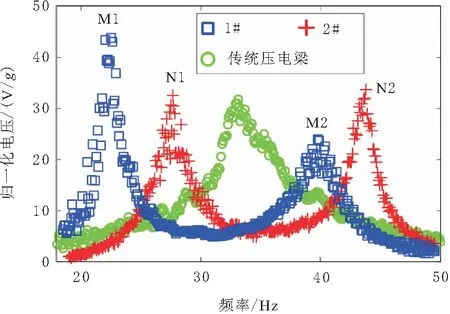
图6 模型1、模型2和传统压电梁的开路电压频响

归一化功率信号定义为：

(2)

R为负载电阻。为了得到最大输出功率，需要选用合适的负载电阻，因此进行了电阻匹配的实验。如图7所示，在0.1 MΩ至3 MΩ的范围内，模型1和模型2均能在0.5 MΩ的负载电阻下获得最大功率输出，因此后面的实验均选用0.5 MΩ作为负载电阻。

图7 模型1、模型2的峰值功率随负载电阻变化情况

图8为模型1和模型2在该负载电阻下的发电功率及通过电路串联时的输出功率频响。模型1前两阶振型的归一化输出功率分别为0.88 mW/g2(22.4 Hz)和0.27 mW/g2(39.8 Hz)，模型2前两阶振型的归一化输出功率分别为0.49 mW/g2(27.6 Hz)和0.53 mW/g2(43.7 Hz)。2个模型的输出功率的前两阶峰值频率间隔都仅为17 Hz左右，且相互错开，通过电路串联可实现4个峰值，进一步拓宽了振动发电有效频响范围。