空间机械臂多目标综合轨迹规划研究
2018-07-25,,
,,
(哈尔滨工业大学机器人技术与系统国家重点实验室,黑龙江 哈尔滨 150080)
0 引言
空间机械臂凭借其在复杂空间环境下高效可靠地执行一系列高难度在轨任务的能力,在人类太空探索的进程中发挥着越来越重要的作用。冗余自由度机械臂由于具有灵活操作的优势,已成功应用于绝大多数的空间机械臂系统。
轨迹规划是机械臂运动控制的基础,是指在运动学和动力学约束的基础上,对机械臂的运动轨迹进行规划。所谓运动轨迹,是指机械臂在运动过程中的位移、速度和加速度[1]。轨迹规划的结果将直接影响机械臂的各项性能指标,考虑到空间机械臂的应用环境,通常期望的空间机械臂性能指标为:1)时间消耗最短[2],尽可能提高空间机械臂的工作效率;2)能量消耗最少[3],满足空间机械臂长时间在轨工作的要求;3)轨迹冲击最小[4],有利于提高运动轨迹的平滑性,保护机械结构。实际应用中,通常需要将以上几个优化目标综合考虑,使机械臂的轨迹规划达到整体最优的效果。
文献[5]使用三次多项式曲线连接相邻的路径点,通过基因环境双演化免疫克隆算法(EGICA),对机械臂的时间消耗和能量消耗指标进行综合优化。文献[6]采用三次样条曲线构造机械臂的运动轨迹,将时间消耗和衡量轨迹冲击性的关节脉动平方值组合成新的优化目标,考虑机械臂的运动学约束条件,使用序列二次规划方法(SQP)得到了优化的运动轨迹。为实现启停时刻的运动学参数可指定,文献[7]采用七次B样条曲线构造机械臂的运动轨迹,但计算过程比较复杂。
在此,首先采用三次均匀B样条曲线构造速度和加速度都连续的空间机械臂关节轨迹。然后分别以机械臂运动的时间消耗、能量消耗和轨迹冲击性作为3个相互独立的优化目标,以机械臂的关节位移、速度、加速度和关节力矩的限制作为约束条件,建立空间机械臂多目标综合轨迹规划问题的数学模型。最后使用带精英策略的非支配排序遗传算法(NSGA- II)进行模型求解。
1 机械臂关节空间轨迹构造
当考虑机械臂的性能指标优化时,轨迹规划通常在关节空间中进行。由于B样条曲线可以分段处理,具有良好的局部支撑性,本节采用B样条曲线来构造空间机械臂的关节空间轨迹。
1.1 B样条曲线理论基础
k次B样条曲线的表达式为[8]:
(1)
di(i=0,1,…,n)为曲线的控制顶点,又称德布尔点。通常为了得到经过给定路径点(又称型值点)Pj(j=0,1,…,m),m=n+1-k的关节轨迹,需要反求出B样条曲线的控制顶点。Ni,k(u)称为k次规范B样条基函数,其中每一个称为规范B样条,简称B样条。它是由一个称为节点矢量的非递减的参数u的序列U:u0≤u1≤…≤ui+k+1所决定的k次分段多项式,也即k次多项式样条。Ni,k(u)的双下标中,k表示次数,i表示序号。B样条有多种不同形式的等价定义,本文采用德布尔- 考克斯递推公式[9]定义,其表达式为:
(2)
该递推公式表明,欲确定第i个k次B样条,需要用到ui,ui+1,…,ui+k+1共k+2个节点,故称区间[ui,ui+k+1]为Ni,k(u)的支撑区间。
1.2 三次均匀B样条曲线构造
为了得到速度和加速度连续的关节轨迹,在此,采用三次均匀B样条曲线构造空间机械臂的关节轨迹。所谓“均匀”是指节点矢量中的节点沿参数轴均匀或等距分布,所有节点区间长度一致Δi=ui+1-ui=Δ>0(i=0,1,…,n+k),其中Δ为某一确定的常数[10]。由B样条曲线方程可知,当k=3,i=0,1,2,3时,三次均匀B样条曲线基函数分别为:
(3)
将式(3)代入式(1)可得用矩阵形式表示的三次均匀B样条曲线方程为:
(4)
其中,u∈[0,1]。
空间机械臂关节轨迹的构造过程是在多个给定的相邻型值点之间分别插入一段B样条曲线,又已知型值点的值为式(4)中Pi取u=0时的值,即:
di+4di+1+di+2=6Pi(i=0,1,…,n-2)
(5)
以上共n-1个方程,再补充2个条件[11]:
长江天鹅洲白鱀豚国家级自然保护区于 1992年经国务院批准建立,辖长江89 km石首江段和天鹅洲故道,该区域生态环境的优劣直接关系到生活于其中的保护动物如白鱀豚(Lipotes vexillifer)和江豚(Neophocaena asiaeorientalis)等栖息环境的好坏,进而影响其种群的正常繁衍和维系。本研究以湖北石首长江天鹅洲白鱀豚国家级自然保护区附近长江河段(89 km)为研究对象,采用多元统计方法,研究该河段浮游动植物群落结构及季节变化,探讨浮游动植物之间的相互关系,为该区域生态系统保护与研究工作提供基础资料和科学依据。
d0=d1,dn-1=dn
(6)
由式(5)和式(6)即可求出三次均匀B样条曲线的所有n+1个控制顶点di(i=0,1,…,n)。
2 多目标轨迹规划问题的数学模型
本节建立空间机械臂多目标轨迹规划问题的数学模型,包括目标函数和约束条件2部分内容。
2.1 目标函数
所研究的空间机械臂有7个关节,假设对于机械臂的第n(n=1,2,…,7)个关节,分别给定m+1个关节轨迹的型值点Pnj(j=0,1,…,m),这些型值点将机械臂每个关节的运动轨迹都分为m段。考虑空间机械臂在实际应用中的需求,定义如下3个优化目标[12]:
(7)
(8)
(9)
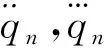
2.2 约束条件
在空间机械臂多目标轨迹规划的过程中,考虑将机械臂的关节位移、速度、加速度和关节力矩的限制条件作为轨迹规划的约束条件:
(10)

3 多目标综合优化问题求解
本节采用NSGA- II算法求解机械臂的关节轨迹,获得空间机械臂的多目标综合轨迹规划问题的Pareto最优解集。相比较传统的加权系数法,采用这种方法进行综合目标优化问题求解可以获得一个最优解的集合,而不是单独的一个优化解,用户可以根据使用需求在这个集合中选择期望的最优解。
3.1 Pareto最优解集的定义
首先给出几项关于Pareto最优解集的定义。
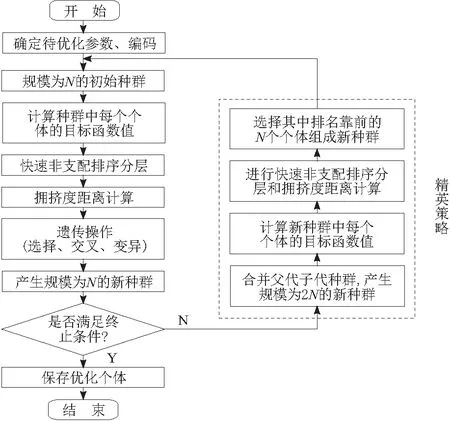
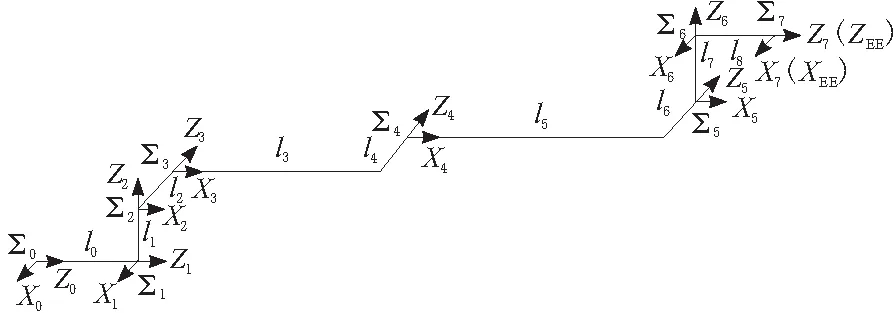
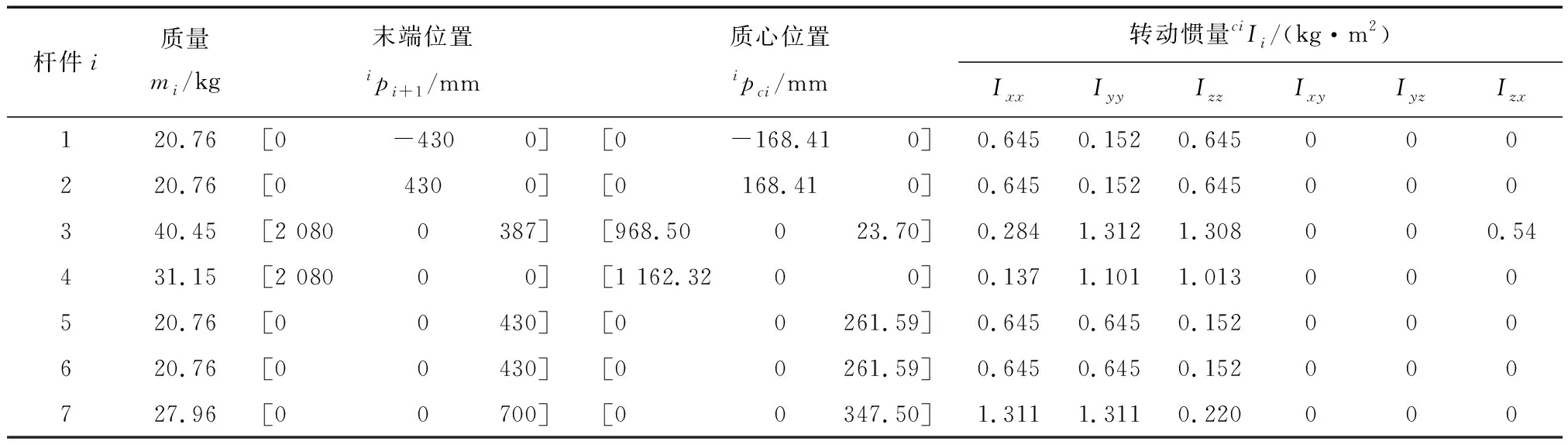
a. Pareto支配关系。以目标函数最小化问题为例,对于具有n个目标分量的最小化多目标向量F(X)=(f1(X),f2(X),…,Fn(X)),任意给定2个决策变量xu,xv∈X(可行解集合),当且仅当,∀i∈{1,2,…,n},fi(xu) b. Pareto最优解集。在整个解空间中均不被其他解支配的所有解构成的集合,称为Pareto最优解集。Pareto最优解具备一个特点:即无法在改进任意一个目标函数的优化值时,不削弱其他至少一个目标函数的优化值,即在保证不削弱其他的优化目标的情况下,该目标是最优的。 c. Pareto最优前沿。对于组成Pareto最优解集的所有Pareto最优解,其对应的目标空间中的目标函数向量所构成的曲面称作Pareto最优前沿。 2002年,Deb提出了带精英策略的非支配排序遗传算法(NSGA- II)[13],成为一种广泛应用的多目标综合优化问题求解方法。NSGA- II采用快速非支配排序机制,驱使搜索过程快速收敛到Pareto最优前沿;同时通过引入精英保留策略,扩大采样空间,将父代种群与其产生的子代种群组合,共同参与竞争产生下一代种群,这样更有利于种群中的优良个体进入下一代,从而提高种群的整体水平;同时定义了拥挤度和拥挤度比较算子,保证Pareto最优解集具有良好的多样性。NSGA- II的算法流程如图1所示。 图1 NSGA- II算法流程 本节对空间机械臂进行多目标轨迹规划仿真验证研究,首先给出空间机械臂各个关节的轨迹型值点和轨迹规划的约束条件,然后考虑机械臂的时间消耗、能量消耗和轨迹冲击性3个指标因素进行多目标综合优化。最后使用NSGA- II算法进行空间机械臂的多目标综合优化问题求解。 本文研究对象为“3- 1- 3”构型的七自由度的冗余空间机械臂,且所有关节均为转动关节,其连体坐标系如图2所示,其动力学参数如表1所示。假设给定空间机械臂执行某次任务时的关节轨迹型值点和机械臂各个关节的运动学和动力学约束条件如表2所示。 采用三次均匀B样条曲线构造空间机械臂的关节轨迹,将以上机械臂各个关节的轨迹型值点代入式(5)和式(6)中,即可求得机械臂各个关节轨迹的控制顶点,将其列于表3中。然后可分别求得机械臂各个关节轨迹的位移、速度和加速度,进而通过逆动力学算法求得机械臂的各个关节力矩,由此可建立空间机械臂轨迹规划的各项约束条件。 图2 七自由度冗余空间机械臂连体坐标系 表1 七自由度冗余空间机械臂动力学参数 表2 机械臂各关节轨迹的型值点和约束条件 表3 机械臂各关节轨迹的控制顶点 针对以上所描述的空间机械臂多目标综合轨迹规划问题,设计NSGA- II算法进行计算求解:以机械臂通过各段轨迹的运行时间作为决策变量,各决策变量之间相互独立;以机械臂各个关节的位移、速度、加速度和关节力矩作为约束条件;以机械臂某段轨迹的时间消耗、能量消耗和轨迹冲击性作为3个相互独立的优化目标。采用浮点数编码方式,采用算数交叉算子和高斯变异算子,设计NSGA- II算法的主要运行参数如表4所示。 表4 NSGA- II算法的主要参数设计 本节使用NSGA- II算法对空间机械臂多目标综合优化问题进行求解(为了排除机械臂运动速度极端慢的不合理情况,除机械臂自身的运动学和动力学约束外,另外设定机械臂的总运动时间最多不超过100 s的条件)。考虑机械臂的时间消耗、能量消耗和轨迹冲击3个优化目标,采用NSGA- II算法计算求解获得的Pareto最优前沿如图3所示。 图3 空间机械臂轨迹规划的Pareto最优前沿 图3中,Pareto最优前沿上的A点代表时间消耗最小,但能量消耗和轨迹冲击性最大的解;B点代表时间消耗最大,但能量消耗和轨迹冲击性最小的解。另外,图3清晰地展现了时间消耗、能量消耗和轨迹冲击性3个性能指标的相关关系:能量消耗指标和轨迹冲击性指标呈正相关关系,它们共同与时间消耗指标呈负相关关系。 由于空间机械臂的多个性能指标相互之间存在矛盾,采取折中的策略,即选取Pareto最优前沿上A点和B点之间的C点作为空间机械臂多目标综合优化问题的工程解,该点的性能指标值为:运行时间为52.887 s;关节平均加速度为2.113 (°)/s2;关节平均脉动为0.555 (°)/s3。对应的机械臂关节轨迹时间变量取值为:Δt1=7.528 s;Δt2=10.428 s;Δt3=11.273 s;Δt4=13.317 s;Δt5=10.341 s。由以上求解结果即可获得机械臂各个关节的位移、速度和加速度曲线,结合逆动力学计算方程,也可获得机械臂各个关节的力矩变化曲线。将以上结果用图4表示,其中图上的虚线表示机械臂的对应约束条件所限定的最大值。 图4 机械臂关节位移- 速度- 加速度- 力矩变化曲线 对七自由度冗余空间机械臂进行了多目标综合轨迹规划研究,主要研究结论有: a.通过三次均匀B样条曲线可以构造速度和加速度都连续的空间机械臂关节空间轨迹,且具有较高的计算效率。 b.采用NSGA- II算法求解冗余自由度空间机械臂多目标轨迹规划问题,可以获得良好的Pareto最优解集,并且机械臂各个关节的位移、速度、加速度和力矩变化都处于安全区间内,且不存在突变的情况,这在工程上是安全可靠的。 c.用户根据使用需求在Pareto最优解集内选取工程解,可以获得满足期望的机械臂运动轨迹,并且此时机械臂的多个性能指标能够达到综合最优的状态。3.2 基于NSGA- II算法的Pareto最优解集求解
4 仿真验证
4.1 优化问题的描述
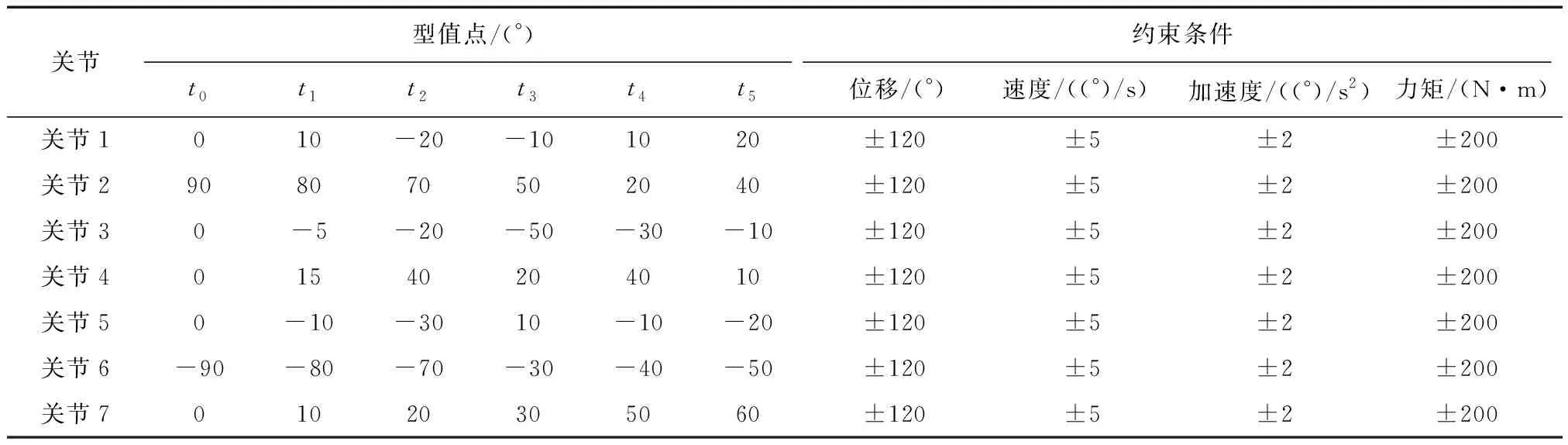
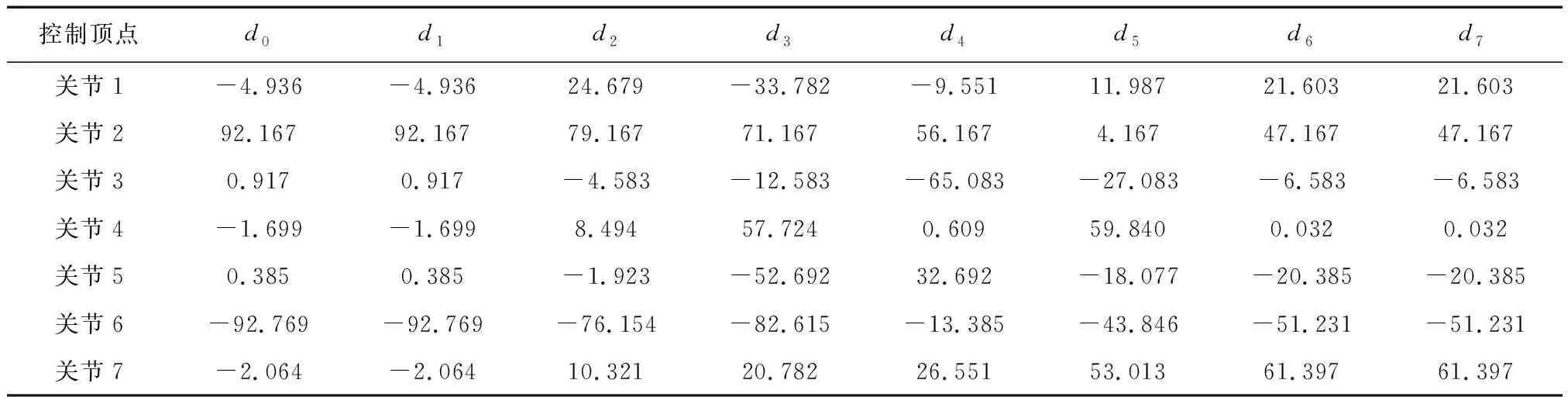
4.2 NSGA- II算法的设计

4.3 多目标综合优化结果及分析


5 结束语
