云南松不同区域相容性生物量模型的构建
2018-07-25刘薇祎邓华锋黄国胜王雪军
刘薇祎,邓华锋,黄国胜,王雪军,张 璐
(1 北京林业大学 林学院,北京 100083;2 国家林业局 调查规划设计院,北京 100714)
森林生物量是评价森林生态系统结构和功能的重要指标,随着森林生态系统与全球气候变化、陆地碳汇等过程的联系越来越紧密,世界各国对森林生物量的监测和评估也越来越重视[1-4]。一般情况下,建立适合较大范围的通用性立木生物量模型针对的是总生物量、地上生物量和地下生物量,但在研究森林生产力和营养物质分布时,需要将总生物量进一步分解成干材、干皮、树枝和树叶等不同的组成部分[5],而传统的生物量回归模型是独立拟合的,不能满足地上总生物量等于各分项生物量之和的要求,从而导致外业调查和数据统计结果不一致[6]。因此,如何合理地构建森林地上生物量相容性模型一直备受重视。
目前,已有众多国内外学者对相容性生物量模型进行了大量研究。在国内,骆期邦等[7]针对生物量总量与各分项生物量不相容的问题,提出了线性联立模型和非线性联合估计模型,并得出非线性联合估计模型优于线性联立模型;曾伟生等[8]以马尾松为例进行了相容性生物量方程的研究,对比分析了比值函数下分级联合控制和总量直接控制2种方案;符利勇等[9]利用比例平差和非线性联立方程组2种方法,建立了南方马尾松不同林分起源的相容性生物量模型。在国外使用较多的是Parreso提出的似然无关回归方法[10],用该法来解决生物量方程的相容性问题。尽管目前生物量相容性模型已被广泛运用,但在构建模型时考虑地域因素的作用和影响的研究仍较少。但在实际中,同一树种在不同区域生物量可能有较大差别[8],因此在保证不同地域对森林生物量模型的影响和大范围内森林生物量估计值可靠性的前提下,分地理区域合并建模是值得研究的问题[11]。为此,本研究以四川、西藏和云南150株云南松地上生物量实测数据为基础,在引入哑变量[12-14]的前提下,利用非线性度量误差联立方程组法,采用比例总量直接控制及代数和控制2种方案构建方程,研究不同区域云南松地上总生物量与树干、干皮、树枝和树叶等各分项生物量相容的生物量通用模型,以期为云南松生物量建模和监测工作提供技术支撑。
1 材料与方法
1.1 数据来源
本研究所用数据来源于全国第八次森林资源清查生物量调查项目,共150株样木,采集地点为四川、西藏、云南3个省(自治)区。为了保证样本在大尺度范围下具有广泛的代表性,样本单元数的选取大致按各省资源量分配,即四川20株,西藏50株,云南80株,各径阶的样本数尽量均匀分布。所有样木均实测胸径、地径和冠幅,将样木伐倒后测量树高和冠长,分干材、干皮、树枝和树叶称鲜质量,并分别抽取样品带回实验室,在85 ℃恒温下烘干至质量稳定,统计得到样木各部分干质量数据并汇总推算得到地上部分干质量。样木基本情况见表1。
1.2 基础模型
近年来,国内外很多学者对生物量模型做了大量研究,并得到多种经验模型[15-18]。目前大部分生物量模型都是以胸径、树高、冠幅、年龄等为解释变量,前人的研究结果表明,随着解释变量个数的增加,模型的预估精度也随之提高,但只有一元到二元的变化对模型效果的提升最明显,而且在实际应用中,林木冠幅和年龄的测定繁琐复杂[19],因此在前人研究的基础上,本研究主要探讨地上生物量与胸径、树高之间的回归关系[20-21],所对应的一元、二元生物量模型表达式如下:
Wi=fi(x)=aDb。
(1)
Wi=fi(x)=aDbHc。
(2)
式中:Wi(i=0,1,…,6)分别为地上总生物量及树干、干材、干皮、树冠、树枝和树叶生物量,D为胸径,H为树高,a、b、c为待估参数。
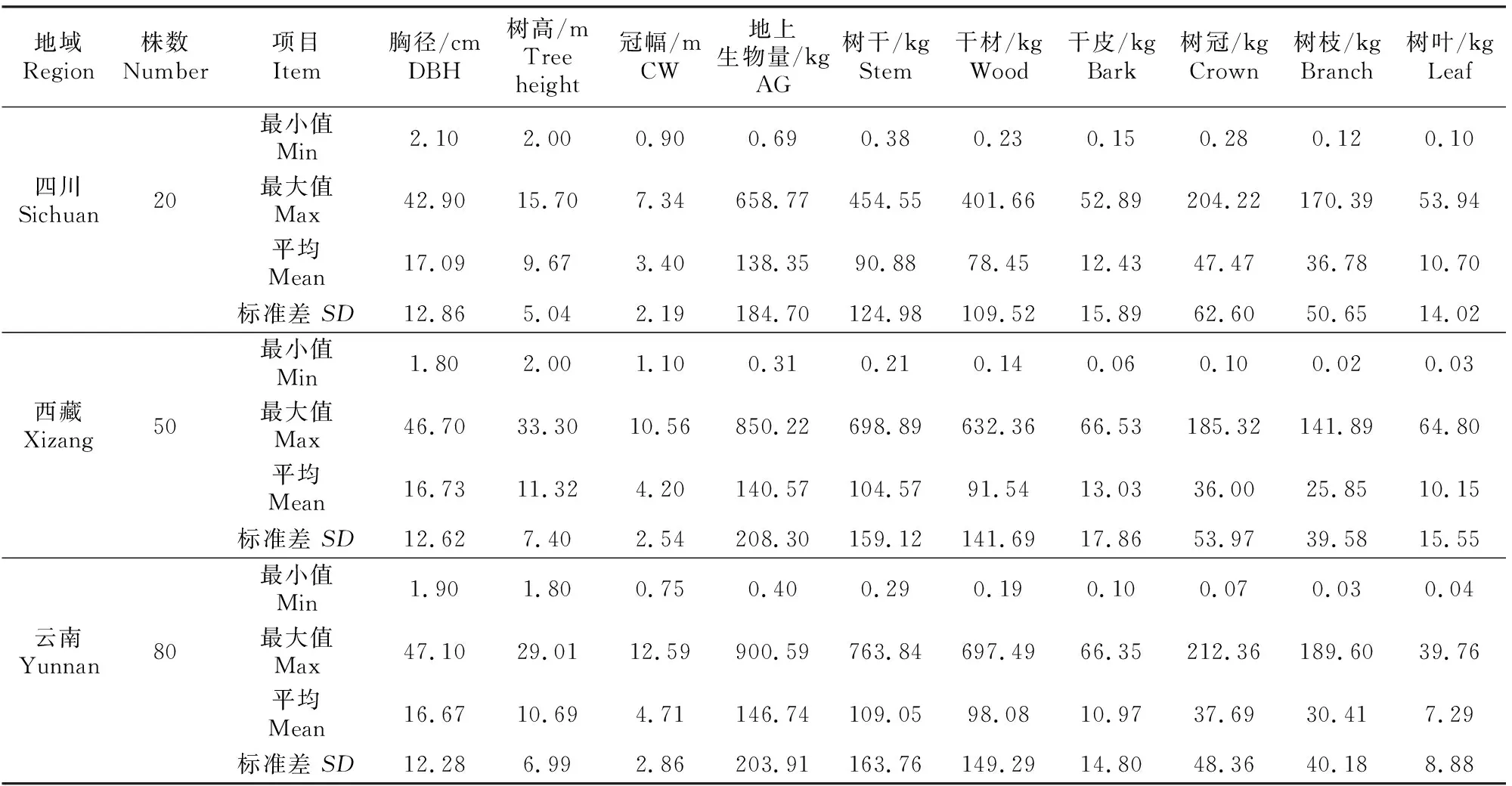
表1 云南松生物量建模样本基本情况Table 1 Basic information of Pinus yunnanensis samples used for biomass modeling
1.3 哑变量模型
哑变量的定义为:对于等级性(定性)数据x,用变量δ(x,i)表示成:

这种方法叫做定性因子(0,1)化展开,因此称变量δ(x,i)为哑变量。一个定性变量(m个等级)对应一个向量δ(x0,)=(δ(x,1),…,δ(x,m)),这样就可将定性变量转换为数值向量进行处理[22]。本研究引入以地理区域为特性的哑变量,构建四川、云南和西藏3个区域的云南松通用性生物量模型,所建模型具体如下:
Wi=fi(x)=(ai+a1iS1+a2iS2)D(bi+b1iS1+b2iS2)。
(3)
Wi=fi(x)=(ai+a1iS1+a2iS2)D(bi+b1iS1+b2iS2)
H(ci+c1iS1+c2iS2)。
(4)
式中:S1=1、S2=0时为四川省,S1=0、S2=1时为云南省,S1=0、S2=0时为西藏自治区;ai、bi、ci为待估参数,a1i、a2i、b1i、b2i、c1i、c2i为哑变量S1、S2的特定参数。
1.4 相容性生物量模型
传统的独立回归模型是在不考虑相容性的情况下得到的最优估计,但是考虑相容性以后可能就不再是最优估计了,为此唐守正等[23]提出了非线性模型联合估计方法,即多元非线性误差变量联立方程组法,其向量形式为[22]:
(5)
式中:f是m维向量函数;yi是p维误差变量的观测数据;xi是q维无误差变量的观测数据;Yi是yi的未知真值;c是参数;ei是度量误差;E(ei)是ei的期望;cov(ei)=σ2φ为误差的协方差矩阵,其中φ是ei的误差结构矩阵,σ2为估计误差。
目前已有很多学者在此基础上又做了许多相关研究[24-25],但方程结构都比较复杂。本研究在前人研究基础上,尝试直接用比例总量直接控制及代数和控制2种结构相对简单的方案,采用非线性度量误差模型方法构建各分项生物量方程系统。
1.4.1 比例总量直接控制 比例总量直接控制法,即将地上生物量直接按比例分配给干材、干皮、树枝和树叶,从而保证各分项生物量之和等于地上生物量总量[20]。具体计算公式如下:
(6)
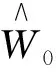
1.4.2 代数和控制 直接用各分项生物量传统回归模型及代数和限制条件来构建非线性联立方程组,既保证了参数的最优估计,又保证了地上总生物量等于各分项生物量之和。具体计算公式如下:
(7)
式中:W0为地上总生物量,ε0为误差项。
1.5 异方差
由于生物量数据普遍存在着异方差性,在独立拟合和利用度量误差联立方程组法拟合时均需要消除异方差,常用的方法是采用对数回归或加权回归[26-28]。由于受方程形式限制无法采用对数回归方法消除异方差,因此本研究结合前人研究,对不同的权函数进行对比分析,最终确定独立拟合的残差平方关于胸径的一元回归模型来做权函数,即在进行参数求解时,每个方程的两侧分别乘以权重变量g(x)。
g(x)=1/g(D)。
式中:D为胸径。
1.6 模型评价
为了对不同方法所建立的模型进行比较分析,本研究采用R2(确定系数)、TRE(总相对误差)、SEE(估计值的标准误差)、MPE(平均预估误差)和AIC(信息量准则) 5项统计指标[29],同时将所构建模型与其相对应的基础模型进行比较。其计算公式为:
(8)
(9)
(10)
(11)
AIC=2p+nln (RSS/n)。
(12)
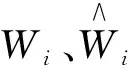
1.7 数据分析
本研究所有数据分析均在Forstat和Excel上完成。
2 结果与分析
2.1 云南松生物量基础模型
150株云南松地上总生物量和各分项生物量的权函数见表2,对云南松生物量样本一元、二元常规模型和哑变量模型(即模型(1)~(4))进行加权回归拟合,并计算各模型的评价指标,结果见表3。

表2 云南松各项生物量模型的权函数Table 2 Weight functions for each biomass model of Pinus yunnanensis
注:W0.地上总生物量;W1.树干生物量;W2.干材生物量;W3.干皮生物量;W4.树冠生物量;W5.树枝生物量;W6.树叶生物量;D.胸径。下同。
Notes:W0.Above-ground biomass;W1.Stem biomass;W2.Wood biomass;W3.Bark biomass;W4.Crown biomass;W5.Branch biomass;W6.Leaf biomass;D.Diameter.The same below.
由表3可知,云南松地上总生物量的常规模型和考虑地域因素的哑变量模型的拟合效果均较好,R2值在0.92左右;地上各分项生物量中除树叶生物量以外,其余各项的R2值也多在0.80以上。通过对一元、二元模型的对比分析可知,自变量个数增加后,各分项生物量模型的R2值明显提高,平均预估误差(MPE)降低(例如干材生物量常规模型的MPE从9.04%降到了5.51%),且其他几个评价指标也相应优化。对常规生物量模型和考虑地域因素的哑变量生物量模型的对比分析可知,引入哑变量后各项生物量模型的AIC值明显降低,且R2值均相应提高,其中树叶生物量模型的R2值提升最为明显,如二元模型由0.663 6提高到0.723 9。从表3还可以看出,各项生物量的一元模型引入哑变量后,R2的提高幅度大于二元模型引入哑变量后,这说明不同地理区域之间的一元模型差异较大而二元模型差异较小,即二元模型的地域通用性要优于一元模型。
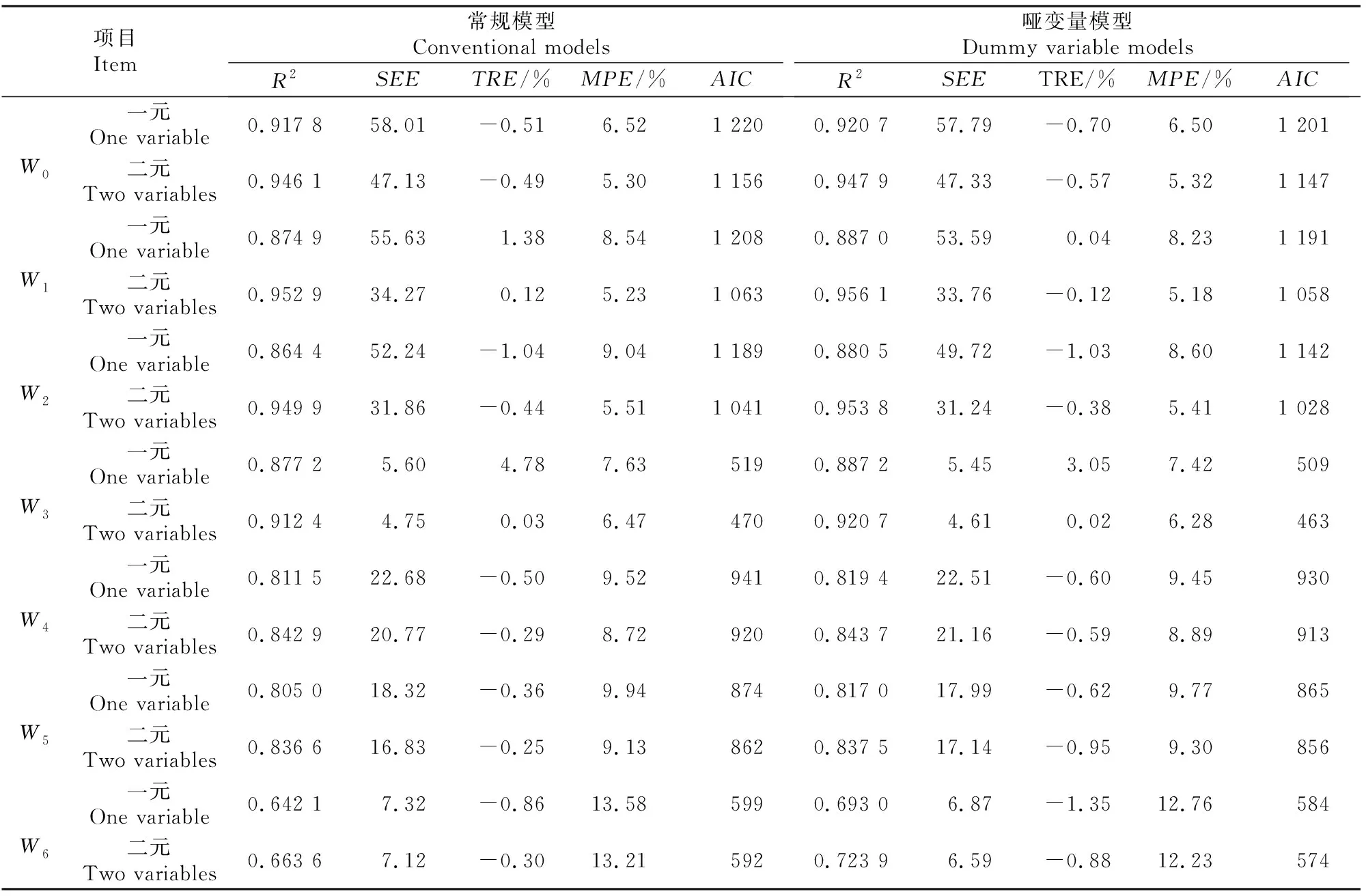
表3 云南松常规模型与哑变量模型的评价结果Table 3 Evaluation of conventional models and dummy variable models of Pinus yunnanensis
2.2 云南松相容性生物量模型
在2.1节研究的基础上,利用一元、二元哑变量模型建立云南松地上总生物量与各分项生物量的非线性度量误差联立方程组,这样既能保证模型之间的相容性,也能减少外业测量带来的误差。各评价指标统计结果见表4。从表4可以看出,比例总量直接控制及代数和控制这2种方案,均满足地上总生物量及树干、干材和干皮生物量预估效果最好,树枝和树冠生物量次之,树叶生物量预估效果最差的结论。一元模型中,树冠和树枝的代数和控制拟合效果略优于比例总量直接控制,而树干、干材、干皮和树叶生物量模型均为比例总量直接控制效果更佳,但这2种方案之间的差异均不是很明显,其中效果差异较为明显的只有树叶生物量,其比例总量直接控制方案的R2值为0.694 9,大于代数和控制方案的R2值0.641 4。而二元模型的比例总量直接控制方案除树枝外,其他几项的R2、TRE等评价指标稍优于代数和控制方案,如干皮生物量比例总量直接控制方案的R2,仅比代数和控制方案的R2大0.010 5。综合总体来看,比例总量直接控制及代数和控制2种方案对云南松相容性生物量模型的拟合效果相差不大。另外对比一元模型和二元模型可知,二元模型中各项生物量模型的R2都在0.831 0以上(树叶生物量除外),平均预估误差都在10%以内,比一元模型拟合预估效果更好。
综上所述,比例总量直接控制及代数和控制2种方案对云南松相容性生物量模型的拟合效果基本相当,在模型表达式方面两者也各有优劣,比例总量直接控制方案的总量模型简单、分量模型复杂,而代数和控制方案的分量模型简单、总量模型复杂;从建模总工作量来看,代数和控制方案更优。一元模型和二元模型也如此,各有其优缺点。因此认为非线性度量误差法一元、二元代数和控制方案所建模型均有实用价值,其模型中各参数值如表5所示。表5中参数a1i与a2i、b1i与b2i、c1i与c2i,即哑变量作用在固定参数上的特定参数明显不相等,与本研究中基础模型的研究结果一致,这进一步说明不同地域云南松生物量之间存在差异。因此,在建立适合较大范围的通用性立木生物量模型时引入哑变量,考虑地域对模型的影响具有现实意义。
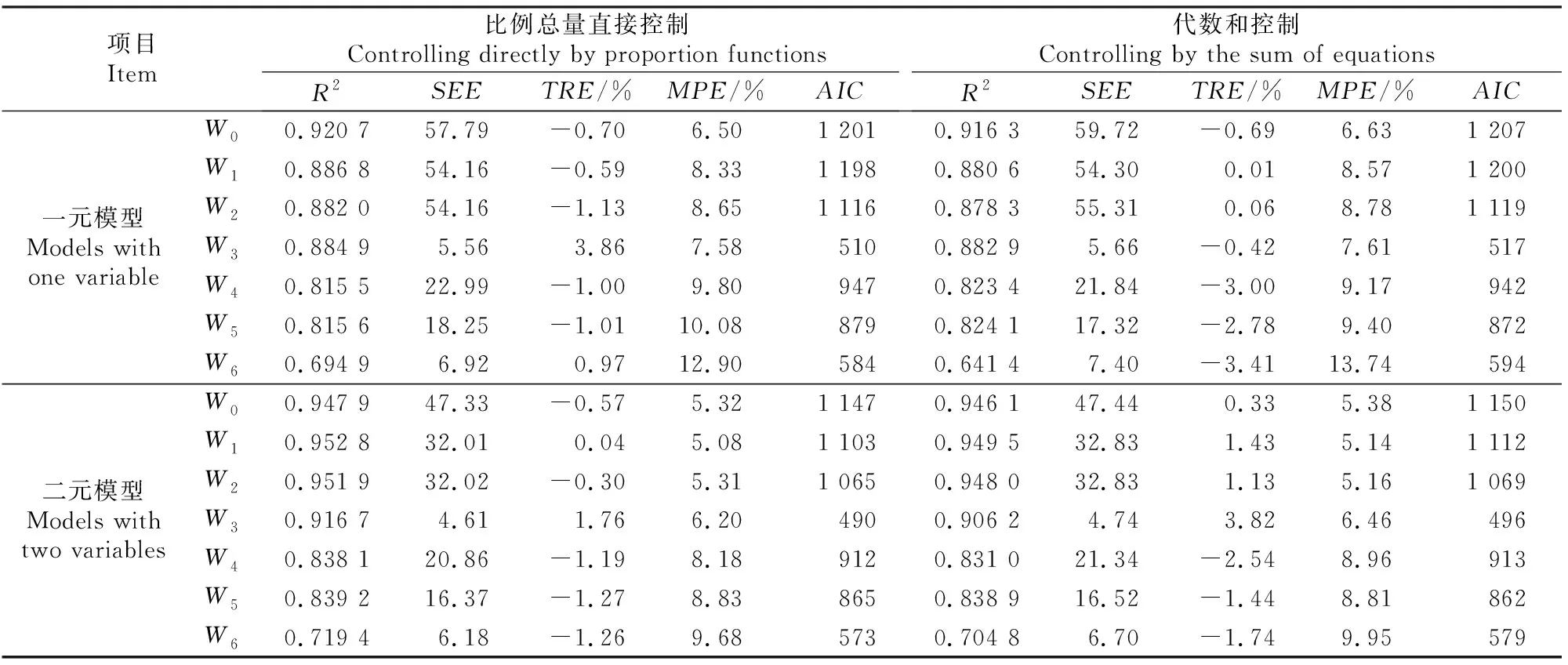
表4 云南松非线性度量误差联立方程组法模型拟合效果的评价Table 4 Evaluation of models with nonlinear simultaneous equations for Pinus yunnanensis
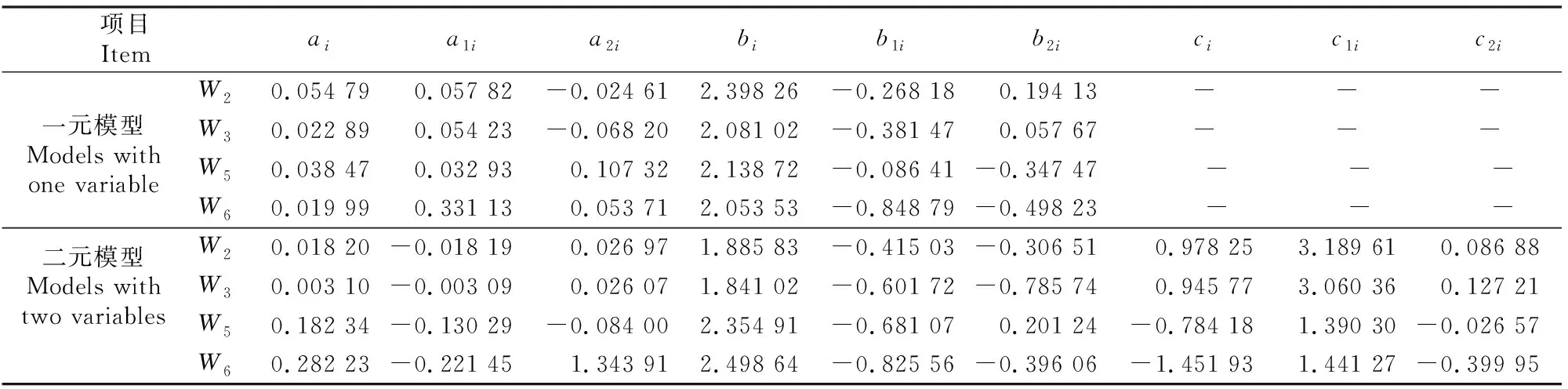
表5 云南松非线性度量误差法一元与二元代数和控制方案所建模型的参数估计值Table 5 Parameter estimation of Pinus yunnanensis models of nonlinear simultaneous methods with one and two predictor variables by sum control
3 讨论与结论
本研究以来自四川、西藏和云南的150株云南松地上生物量实测数据为例,引入以不同地理区域为特征的哑变量,建立了一元、二元回归生物量模型,并对云南松不同区域地上总生物量与各分项生物量的相容性生物量通用模型进行了研究,得出以下结论:
1)从一元模型到二元模型的变化,地上总生物量和各分项生物量模型的各项评价指标与拟合预估效果均有明显优化。但随着自变量个数的增加,建模工作量也会相应增大,而且在进行林业外业调查时,冠幅的测定耗时费力,并且测定结果易受林分结构、地形地势等不确定因素的影响而存在较大误差[9],所以一元、二元模型各有利弊,在实际应用时可根据要求自行选择简单适用的生物量模型。
2)四川、西藏和云南三地由于海拔、经纬度等的差异,导致温度、湿度、气温年较差等气候条件存在差异,而气候条件又是影响云南松生长和地理分布的主要因素[30]。本研究为构建这3个区域的云南松相容性生物量通用模型,引入了以地理区域为特征的哑变量,考虑了其对各分项生物量模型中参数的影响。以模型(7)的二元代数和控制方案为例,通过分析ai、a1i与a2i,bi、b1i与b2i,ci、c1i与c2i的差异可知,不同区域对云南松生物量有影响,这与戴开结等[31]、皮文林等[32]对云南松分布的研究结果一致。由此可知,这种构建哑变量的方法不仅能够减少工作量,还能有效地解决不同区域生物量模型相容性的问题。另外,本研究只探讨了3个不同地域的相容性生物量通用模型,对于多个地域,也可用类似的方法分析多地域对生物量模型的影响,从而建立通用模型。
3)通过比较分析可知,本研究所建立的相容性生物量模型中,比例总量直接控制方案及代数和控制方案的拟合效果相差不大,但在考虑建模总工作量的情况下,代数和控制方案更优,其二元模型的确定系数均在0.831 0以上(树叶生物量除外),最高达0.949 5,地上总生物量的平均预估误差为5%左右,其余各分项的平均预估误差均在10%以内,满足立木生物量的建模要求。本研究只探讨了不同区域的生物量模型建立,在后续研究中可同时考虑区域和树种,利用混合模型的方法建立适用于更大范围不同树种的相容性生物量通用型模型。
