使用角度选择策略的第二代Pareto强度进化算法
2018-07-25罗校清
罗 校 清
(湖南软件职业学院 湖南 湘潭 411100)
0 引 言
进化算法能够不受问题性质(如连续性和非连续性,凹、凸问题,多目标、多约束问题)的限制,有效地处理传统优化算法(如微分法和穷举法)难以解决的复杂问题。在解决只有单个目标的复杂系统优化问题时,进化算法的优势得到了充分展现[1]。在有多个冲突的目标情况下,通常要使得所有的目标都达到最好是不可能的,多目标进化算法MOEA(Multi-Objective Evolutionary Algorithm)[2-3]就是在多个有冲突的目标情况下,寻求一个或者一组折衷解。通常情况下,这种折衷解的集合不唯一,那么如何使求得解的集合尽量好且分布均匀广泛十分重要。
进化优化过程中,获得的解集同时具有好的收敛性和分布性是研究进化算法的目的[4-5],其中,分布性包括分布均匀性和分布广泛性。20世纪末的一些对于进化多目标优化的研究重点在低维目标的优化问题上,研究出了一些非常适用于解决低维问题的MOEAs,如NSGA-II[6]、SPEA2[7]、ε-MOEA[8]、PAES[9]等,这些算法都是基于Pareto支配关系的。基于Pareto支配的MOEA的选择标准主要是以Pareto支配排序为第一个选择标准,以分布性保持机制为第二个选择标准。其中最为广泛使用的是由Deb等[6]提出的NSGA-II。NSGA-II首先将个体按照Pareto支配排序分层,同一层中的个体都是非支配个体,在临界层中使用基于聚集距离的分布性保持机制选取个体填满归档集。由Zitzler[7]提出的第二代Pareto强度进化算法SPEA2与NSGA-II一样使用两个选择标准。SPEA2将个体的分布信息和Pareto支配关系结合到了个体的适应度中,选择适应度大的个体留下,在临界层使用一个修剪方法保持种群的分布性。由Deb提出的ε-MOEA[8]将目标空间划分为网格,使用了基于网格的ε支配方法。这些经典的低维多目标优化算法都使用了Pareto支配关系,并且其提出的分布性保持机制仅仅考虑到了种群的分布性,并没有结合收敛性。
21世纪初,基于分解的多目标进化算法MOEA/D[10]的提出是多目标进化算法研究领域的里程碑。该算法首先将目标分解到不同的方向上,并对应于预先设定的权重向量,由权重的方向来引导个体向不同的方向进化。该算法能获得低维上分布十分均匀的解集。但是,该算法具有以下3点不足:第一,该算法需要提前设置好分布均匀广泛的权重,当目标的数目增加时,如何设置分布性好的权重是一大难点;第二,当目标的个数增加时,设置合适的权重数目是较难斟酌的;第三,该算法选择的个体更加偏向于权重的分布方向,因此在具有退化特性的优化问题上的效果不好。尽管如此,MOEA/D是非常有效的多目标进化算法。自该算法提出以来,受到了国内外学者的广泛关注。
本文针对低维优化问题,提出一种基于角度选择的改进的SPEA2,即SPEA2+。提出包含了个体之间分布性和收敛性的角度选择的分布性保持机制,在临界层中选择个体时,进一步地加强种群的收敛性,同时保持种群的分布性。实验结果表明,当测试问题的目标个数大于3个时,SPEA2+比SPEA2具有更强的收敛性和更好的分布性,且在低维上的综合性能(收敛性和分布性)明显优于其他4个比较的算法。
1 多目标优化问题的数学模型
多目标优化通常涉及到多个目标的同时优化。多目标优化与单目标优化不同,它通常有多个符合条件的最优解,为了说明如何处理多个最优解,首先给出多目标优化问题的数学模型[2]。
给出决策向量x=(x1,x2,…,xn)T,它满足式(1)、式(2)中的约束。
gi(x)≥0i=1,2,…,k
(1)
hj(x)=0j=1,2,…,l
(2)
设有m个优化目标,则优化目标最小化为:
minf(x)=(f1(x),f2(x),…,fm(x))T
(3)
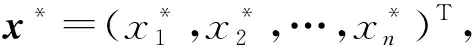
2 Pareto支配关系
当有多个目标时,通常存在一些无法简单比较的解。这种解通常称作非支配解或Pareto最优解。首先给出决策空间和目标空间的定义。
定义1决策变量空间(简称决策空间)的定义:
Ω={x∈Rn|gi≥0,hj(x)=0;(i=1,2,…,k;j=1,2,…,k)}
定义2目标函数空间(简称目标空间)的定义:
Π={f(x)|x∈Ω}
目标函数f(x)将Ω映射到集合Π。
定义3Pareto支配关系
设xa和xb是两个不同的解,称xa支配xb,则必须满足式(4)和式(5)两个条件。
对所有的子目标,xa不比xb差,即:
∀i∈{1,2,…,m}fi(xa)≤fi(xb)
(4)
至少存在子目标,使xa比xb好,即:
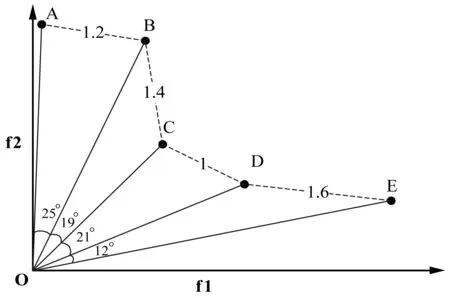
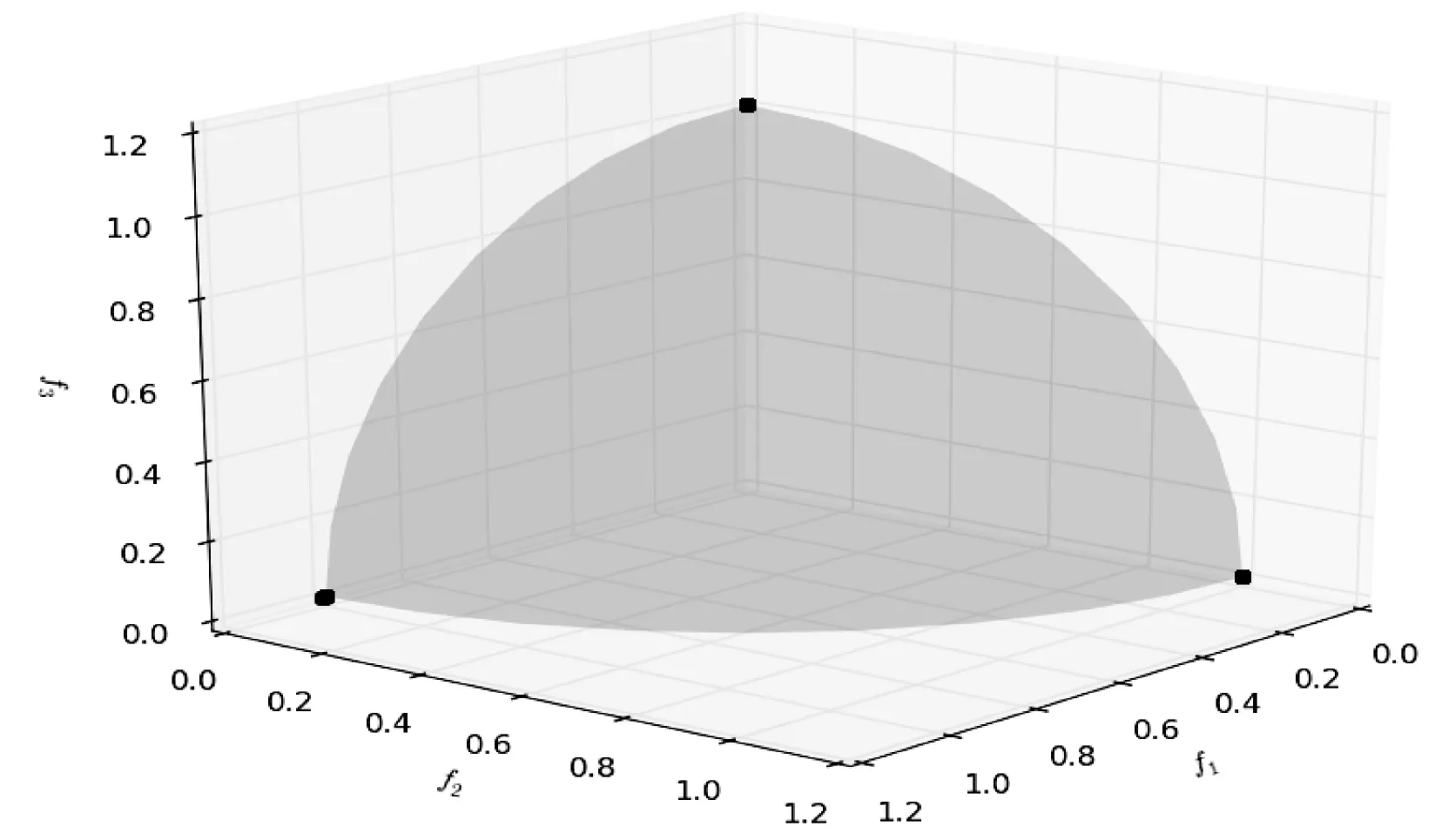
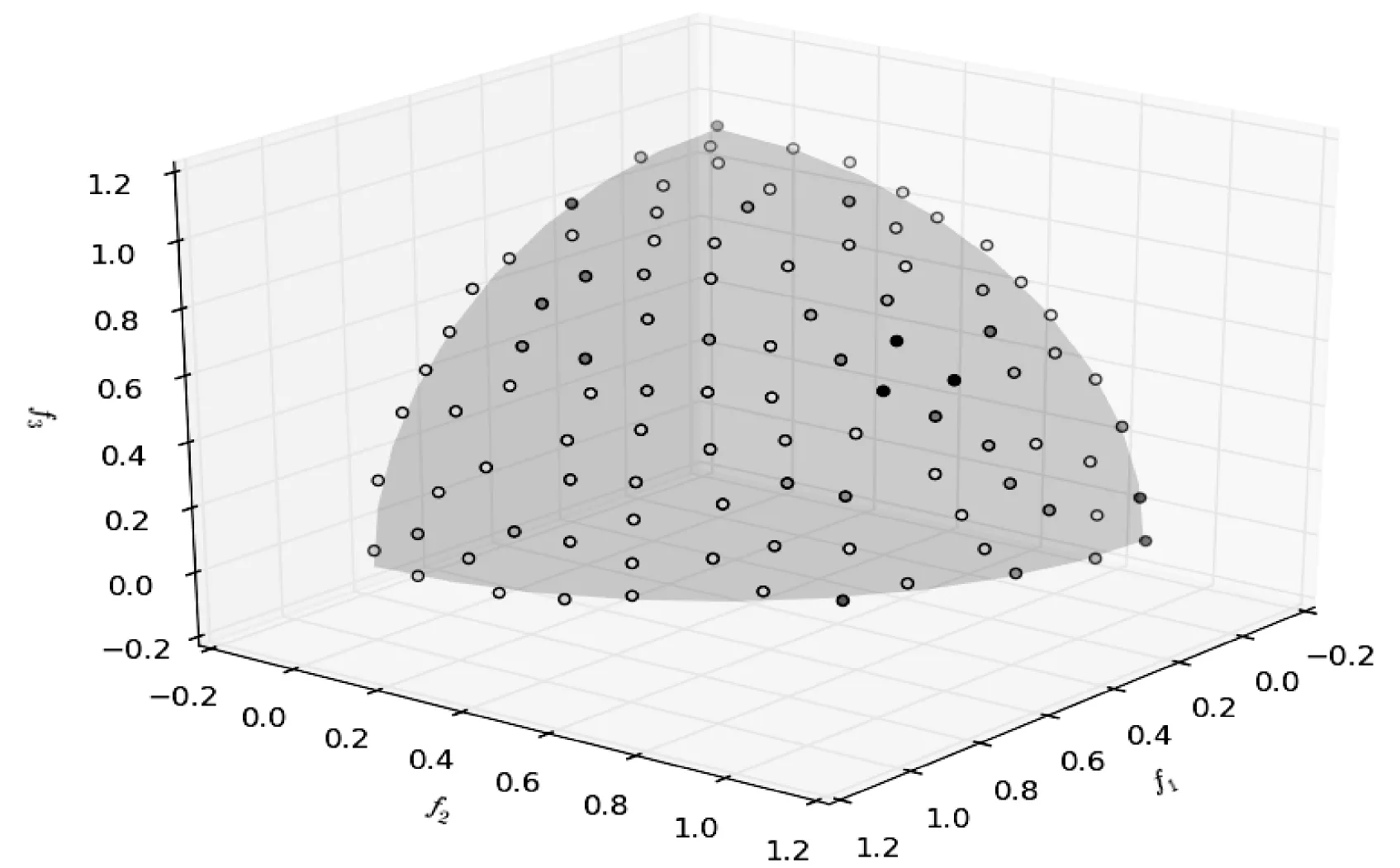
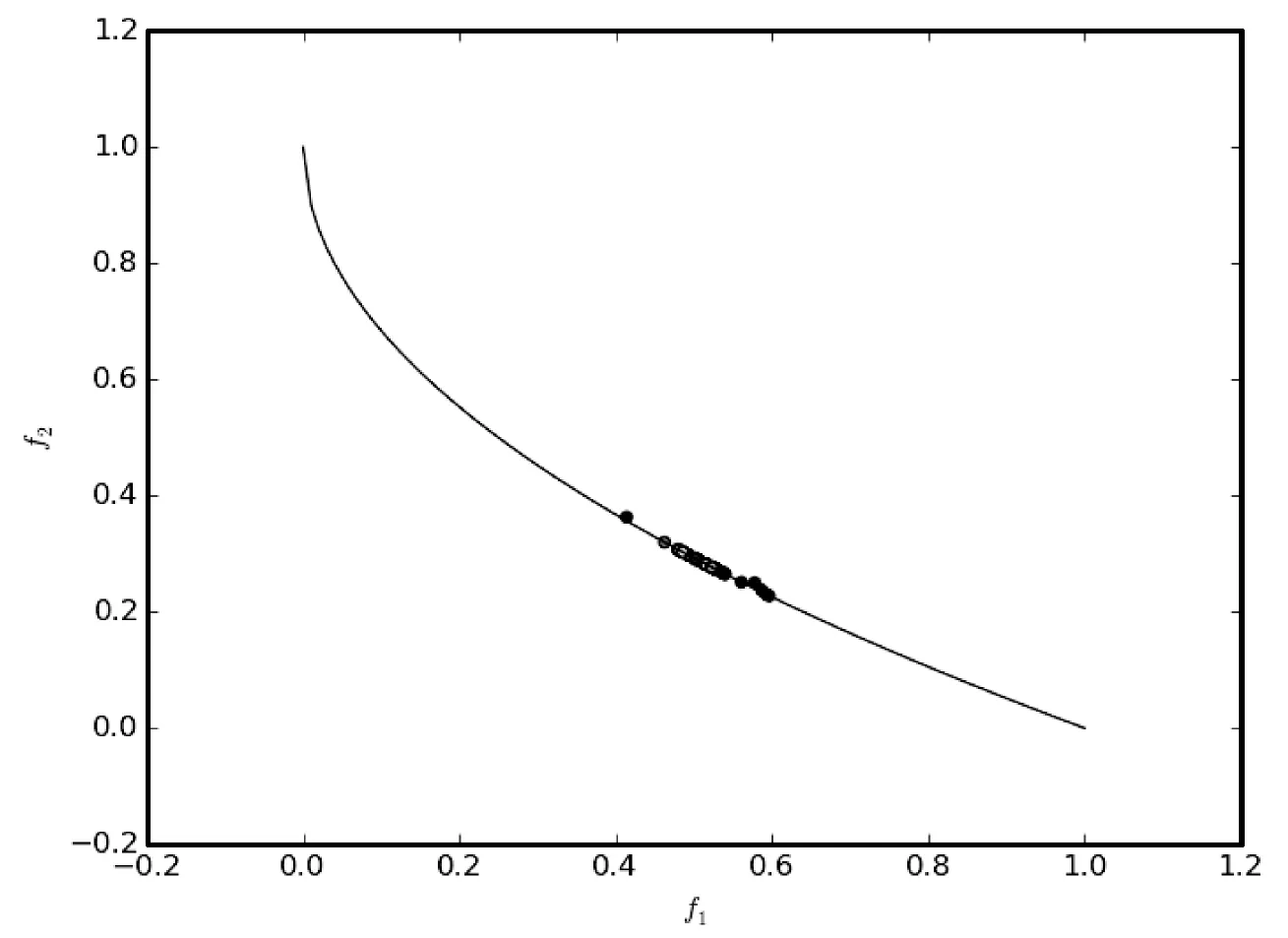
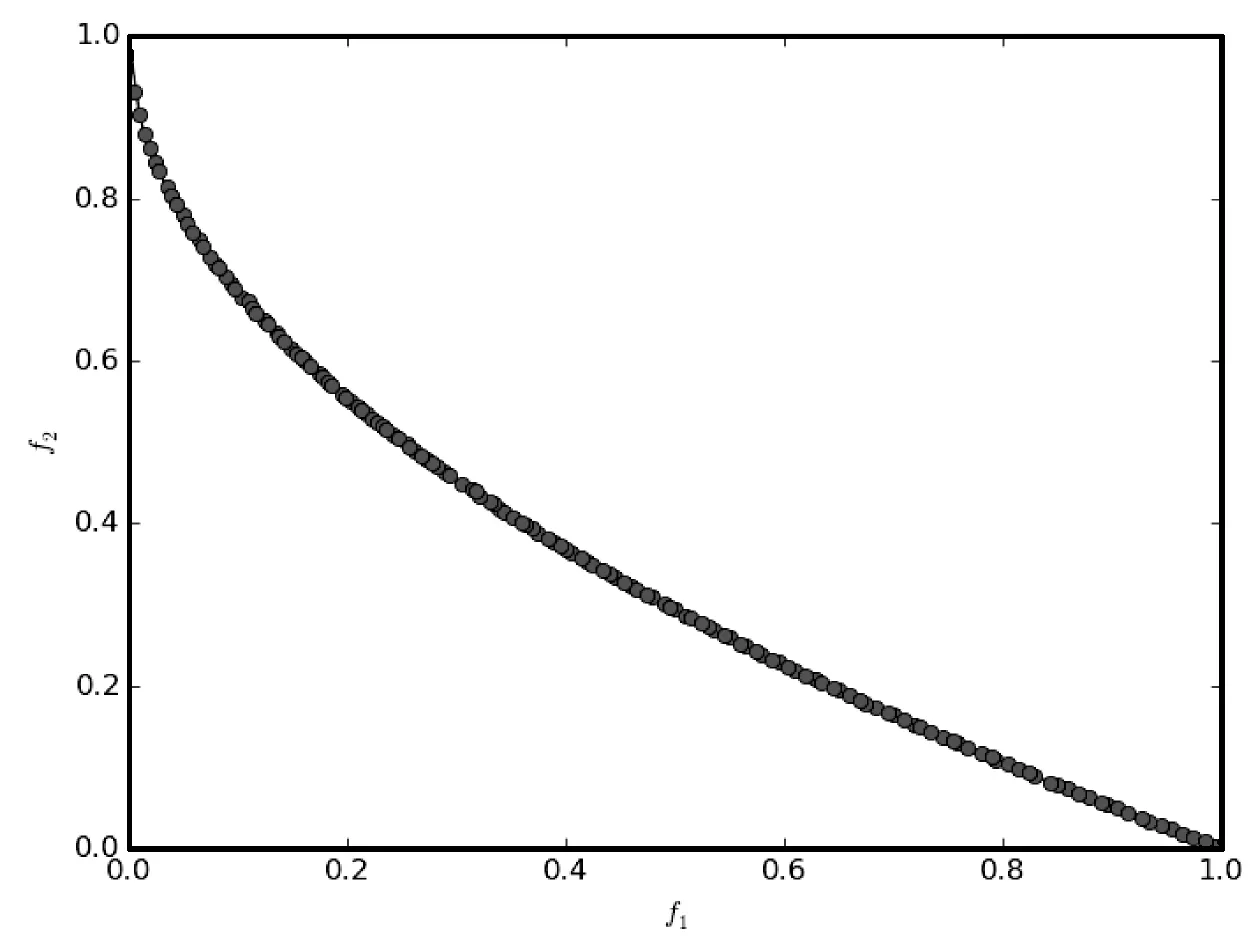
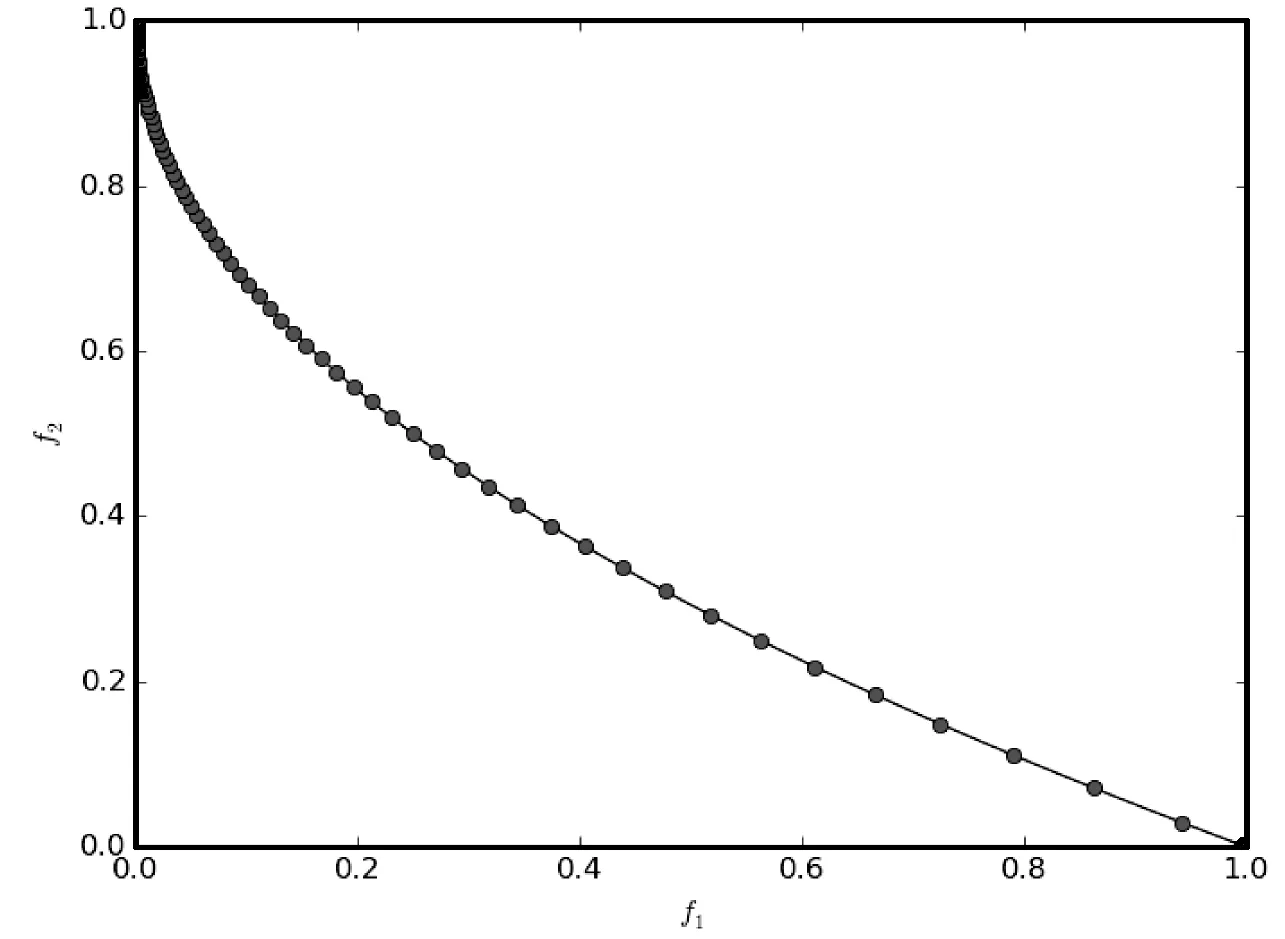
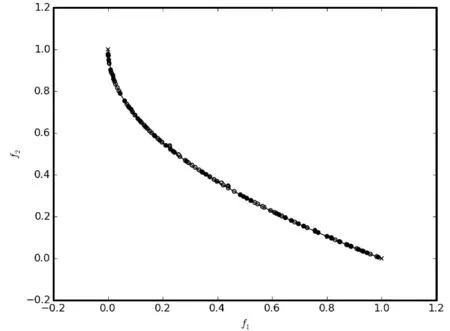
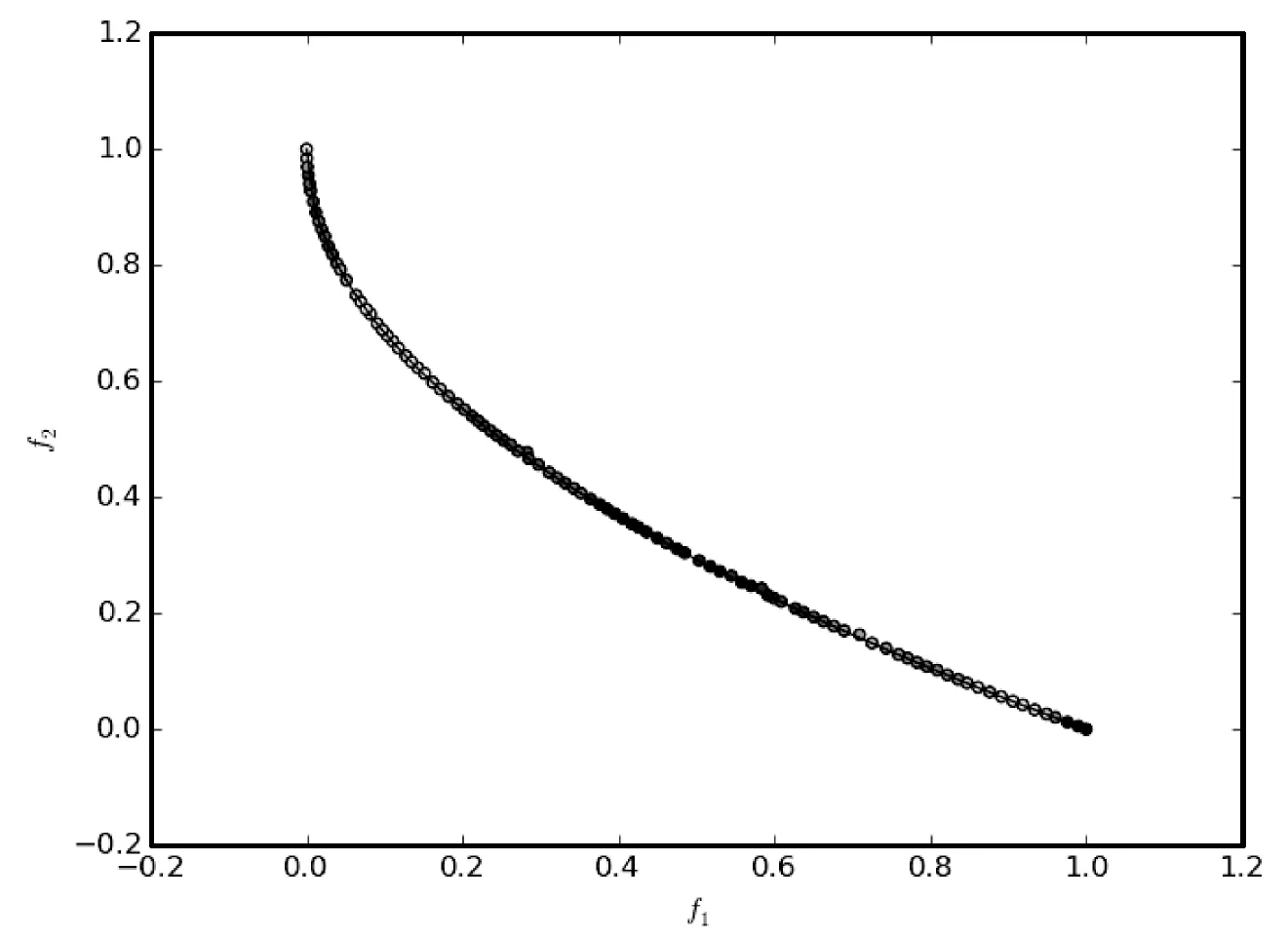
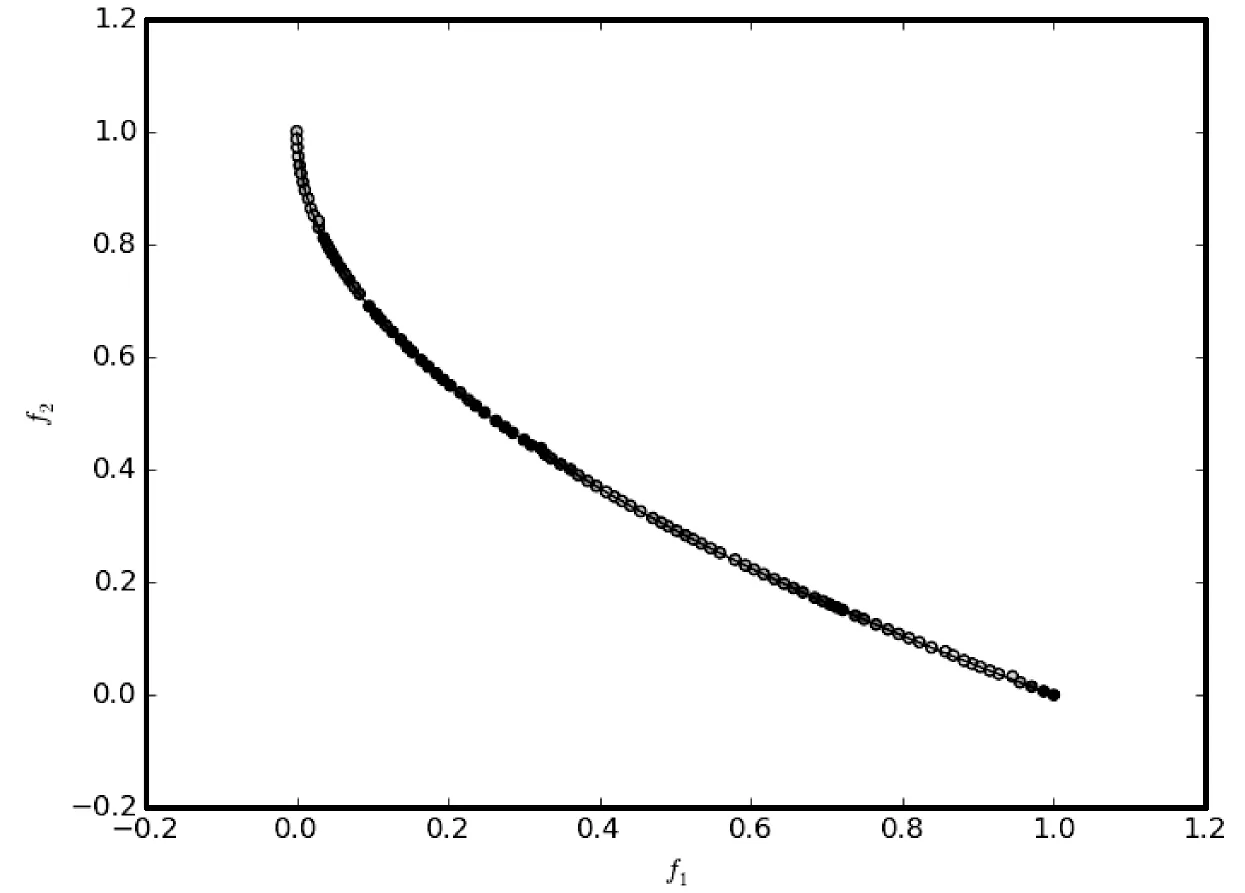
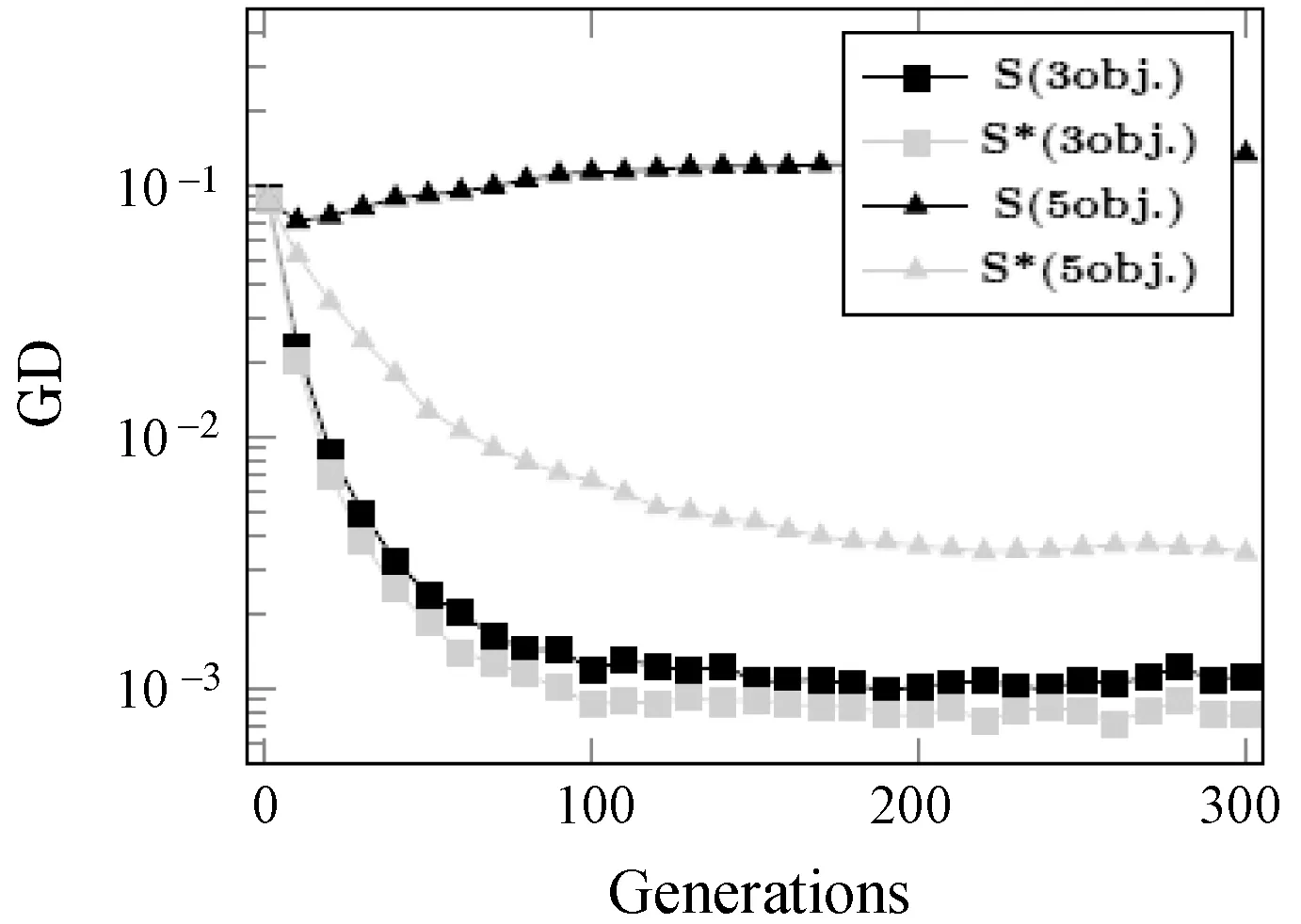
∃j∈{1,2,…,m}fj(xa) (5) 式中:m为子目标的数量。Pareto支配关系表示为xa≻xb,其中“≻”表示支配关系。 第二代Pareto强度进化算法SPEA2(Strength Pareto Evolutionary Algorithm)相比于SPEA[11]在3个方面进行了改进:一个改进的适应度分布策略,其考虑了每个个体支配的个体数目和每个个体被多少个个体支配;第k个邻近个体密度评估机制;一个新的归档集修剪策略用来保留边界个体。 种群中的每个个体分布了一个强度值(strength value),表示个体i在进化群体P和归档集A中支配的个体数,计算公式如下: S(i)=|{j|j∈P+A∧i≻j}| (6) 在强度值S的基础上,个体i的原始适应度值(raw fitness)表示个体i的支配者在进化群体P和归档集A中的强度值之和,计算公式如下: R(i)=∑j∈P+A,j≻iS(j) (7) (8) 当个体i到其第k个邻近个体之间的距离越大,表示个体i的分布性较好,得到的D(i)越小,个体i最终的适应度值也越小(SPEA2的个体适应度越小越好),则该个体被选中进入下一次进化的可能性更大。算法1描述了适应度计算步骤的伪代码。CalculateStrength(P)函数表示计算种群P的强度值S,CalculateRawFitness(P)函数用来计算种群P的原始适应度值R,CalculateKthDistance(P)函数用来计算种群P中的每一个个体的密度值D。rawfitness(x)和KthDistance(x)分别表示个体x的原始适应度值R和密度值D,fitness(x)表示个体x的最终适应度值。 算法1个体适应度赋值的伪代码 输入:种群P={x1,x2,…,xl} 输出:适应度{fitness(x1),fitness(x2),…,fitness(xl)} CalculateStrength(P); CalculateRawFitness(P); CalculateKthDistance(P); FORι=1 TOlDO fitness(xι)=rawFitness(xι)+1/(KthDistance(xι)+2); END FOR 当归档集中的非支配个体超过预设的归档集大小时,使用修剪操作剔除归档集中的非支配个体,使得剩余个体保持较好的分布性。首先计算归档集中每两个个体之间的距离(如函数CalculateDistancetoOthers()),找到最小距离对应的两个个体i、j(函数FindMinDistPoints()),分别找出这两个个体到其他个体之间最小的距离为di、dj(secondMinDist1值和secondMinDist2值),删除这两个距离中较小距离对应的个体i或者j(函数Delete())。循环以上过程,直到归档集中的非支配个体等于预设的归档集大小。修剪操作的流程如算法2所示。 算法2修剪操作的伪代码 输入:归档集A={B;x1,x2,…,xl},归档集大小n 输出:归档集A={x1,x2,…,xn} disMatrix=CalDistancetoOthers(A); WHILE |A|>nDO pair secondMinDist1=FindSecondMinDist(distMartix,first); secondMinDist2=FindSecondMinDist(distMartix,second); IF secondMinDist1 Delete(first); ELSE Delete(second); END IF END WHILE 环境选择是选出进化种群P和归档集A中的精英个体进入下一代进化。首先将进化种群P和归档集A中的所有非支配个体复制到进入下一代进化的归档集A中(函数SelectNondominatedIndividuals()),如果新的归档集A中的非支配个体数目超过了预设的归档集大小,则采用修剪操作(函数Truncate())。如果,归档集中的非支配个体数目不足,则继续从进化种群P和归档集A中选取第一层非支配个体填充满归档集(函数SelectDominatedIndividuals())。环境选择的算法流程如算法3所示。 算法3环境选择的伪代码 输入:种群P={x1,x2,…,xl},归档集大小n≤l 输出:归档集A={x1,x2,…,xn} A=SelectNondominatedIndividuals(P); IF |A|>nTHEN Truncate(A,n); ELSE P*=SelectDominatedIndividuals(P,n-|A|); A=A∪P*; END IF SPEA2算法首先随机产生一个初始化种群(RandomInitiate()),创建一个空的归档集(CreatEmpty()),设置进化代数为0。计算进化群体P和归档集A中所有个体的适应度值(AssignFitness())。对P和A中个体进行环境选择(EnvironmentSelection()),产生子代精英个体,对其进行二进制锦标赛选择(MatingSelection())、交叉(Crossover())、变异(Mutation()),将产生的子代个体放到进化群体P中参与下一代进化。在终止条件满足前循环该过程。SPEA2算法的总体框架如算法4所示。 算法4SPEA2算法流程的伪代码 输入:种群大小n,归档集大小n,终止运行代数τ 输出:归档集A={x1,x2,…,xn} P=RandomInitiate(n); A=CreatEmpty(n); M=P∪A; AssignFitness(M); A=EnvironmentSelection(M,|A|); P=MatingSelection(A); P=Crossover(P); P=Mutation(P); END WHILE 在分布性保持策略中结合收敛性信息,能进一步地提高算法的全局搜索能力。提出使用角度选择策略的第二代Pareto强度进化算法(SPEA2+),该算法保留了SPEA2的总体框架,提出了基于角度选择的分布性保持策略,并将其应用到SPEA2中的环境选择。基于角度选择的分布性保持策略计算种群中每两个个体的夹角,将该夹角作为这两个个体的角度距离。设两个个体为p、q,则它们之间的夹角计算公式如下: (9) 基于角度选择的分布性保持策略的伪代码如算法5所示。函数CalAngletoOthers(A)计算种群A中每两个个体之间的角度距离,函数findMinAnglePoints()找到最小角度距离对应的两个个体,函数findSecondMinAngle()找到某个个体与其他个体的最小角度距离。 算法5基于角度选择的分布性保持策略的伪代码 输入:归档集A={x1,x2,…,xl},归档集大小n 输出:归档集A={x1,x2,…,xn} angleMatrix=CalAngletoOthers(A); WHILE |A|>n DO pair secondMinAngle1=findSecondMinAngle(angleMatrix,first); secondMinAngle2=findSecondMinAngle(angleMatrix,second); IF secondMinAngle1 delete(first); ELSE delete(second); END IF END WHILE SPEA2中的修剪操作计算每两个个体之间的欧氏距离。基于欧氏距离得到的两个个体之间的距离仅仅反映了个体之间的距离的长短(即分布情况),而基于个体之间的夹角计算得到角度距离还能反映个体的收敛情况。例如,当两个个体之间的欧几里得距离较大时,它们之间的夹角很可能较小,因此,使用角度距离能剔除收敛较差,离种群中心点较远的个体,从而增加收敛压力,保持好的分布性。同时,基于角度选择的分布性保持机制能够保留种群中的边界个体,从而保持种群的分布广泛性。 在种群进化过程中,广泛存在图1中的个体分布情况。利用图1来分析基于角度选择的分布性保持机制和使用欧几里得距离的修剪操作删除种群中多余个体的过程。种群中有A、B、C、D和E五个个体,现在需依次从种群中删除两个个体。使用基于角度选择的方法剔除个体的过程是:首先计算五个个体中每两个个体之间的夹角,得到最小的夹角对应的两个个体为D和E;计算与D个体组成的最小的夹角是∠COD,与E组成的最小夹角是∠COE,因为∠COD<∠COE,所以剔除个体D;同样,再剔除个体B。SPEA2中使用欧几里得距离剔除的两个个体为C、B。可以从图1中看到,C个体的收敛性好于D个体,但是SPEA2中的修剪操作将C个体剔除了,而角度选择策略能将其保留,说明该策略具有更强的收敛压力。同时,这两种策略都保留了最靠近边界的两个个体A和E,这样保持了解集的分布广泛性。当优化目标的数目增加时,临界层中的个体数目指数增加,有越来越多的个体需要通过分布性保持策略被选择,因此在分布性保持策略中引入少量的收敛性信息能有效地促进算法的收敛,同时保持较好的分布性。 图1 基于角度选择的分布性保持策略和 SPEA2中修剪操作比较 本节分析SPEA2+的时间复杂度的上界,该算法在每次迭代的过程中,主要有3个操作:1) 匹配选择;2) 重组;3) 环境选择。设定种群的大小为N,需要优化的问题的目标个数为M,则匹配选择的时间复杂度为O(NM),其中两个个体之间比较支配关系的时间复杂度为O(M)。重组过程采用模拟二进制交叉[21]和多项式变异[22],时间复杂度为O(DM),D为决策变量的维数。环境选择包含2个部分:非支配排序选择,角度修剪策略。非支配排序选择的时间复杂度为:O(MN2),角度修剪策略的时间复杂度为O(N2)。因此,环境选择过程的时间复杂度为O(MN2)。可以得出,SPEA2+的时间复杂度为O(GMN2),G是迭代次数。 本文选取了4个经典的多目标进化算法ε-MOEA、NSGA-II、SPEA2、MOEA/D和一个高维多目标进化算法AR[12]与SPEA2+进行对比,来验证SPEA2+的有效性。 在进化多目标优化领域,已有许多研究标准测试集的成果[13-15]。本文选取常用的测试集DTLZ系列测试函数[17]和ZDT系列测试函数(目标数目为2)[14]对6个多目标进化算法进行测试,得到这些算法对特定优化问题的性能。DTLZ系列测试函数选取其中7个测试问题(DTLZ1至DTLZ7),测试函数的目标个数为2和3个;ZDT系列测试函数选取ZDT1、ZDT2、ZDT3、ZDT4和ZDT6这5个测试函数,测试的目标个数为2个。同时,选取了一个带有3个决策变量、5个目标和7个约束的实际应用问题,即雨水排放系统优化问题[16]。该问题描述了一个城市中的雨水排放系统的优化项目。这个问题一般被用来检验多目标进化算法处理高维带约束优化问题的能力[17-18]。该问题的公式如式(10),f1(x)-f5(x)表示5个目标的最小化,g1(x)-g7(x)表示7个约束,其详细的描述可参考文献[14]。 (10) 决策变量的范围:0.01≤x1≤0.45,0.01≤x2,x3≤0.1。 MOEA性能评价指标用来评价MOEA的收敛效果和所求解集的分布效果。本文选择1个被广泛使用的MOEA性能评价指标IGD(inverted generational distance)[19]来评价6个算法的综合性能,即IGD指标能同时评价算法的收敛性和分布性。IGD的定义如下: (11) 式中:n是获得的解集的大小。di=minj∈P|i-j|表示真实Pareto前沿面PF*上的点i到获得的解集P之间的最小欧式距离,j表示该解集中的某个解。IGD指标的值越小,说明获得的解集越靠近真实Pareto面,且分布性好,综合性能越好。IGD的值在闭区间[0,1],说明算法进化得到的种群能够较均匀地逼近真实Pareto前沿面,且收敛。选取经典的评价多目标算法的收敛性的指标generational distance(GD)[20]来评价SPEA2+和SPEA2的收敛性。GD是IGD的逆映射。GD值越小,说明获得的解集越靠近真实Pareto面。GD的值在闭区间[0,1],说明解集已经收敛到真实Pareto前沿面。 本文比较的每个算法在每个测试用例上独立重复运行30次获得最终的实验数据。种群和归档集中的个体数目设置为100。使用实数模拟二进制交叉(SBX)[21]和多项式变异(PM)[22]。交叉概率为1,变异概率为1/n(n表示种群大小)。 特别地,MOEA/D中选择的聚合函数为weight sum函数[10],邻居种群的大小设置为初始种群数目的10%,惩罚参数设置为5。 本节给出6个多目标进化算法在DTLZ1至DTLZ7的7个测试问题上的IGD指标值,如表1所示。表中单元格中的数据分别为30次独立重复实验的均值和标准差(括号内),加粗的数据表示在每个测试用例上表现性能最好的指标值。 表1 6个多目标进化算法在DTLZ测试集上的IGD指标值 根据表1分析6个多目标进化算法在低维测试问题上的性能。SPEA2+的综合性能最好,其中它的IGD值在6个测试用例上排第一;其次是SPEA2和ε-MOEA;其他3个算法表现一般。SPEA2在2目标测试问题上的综合性能优于SPEA2+,但是SPEA2+在3目标测试问题上的综合性能更好,这是因为随着目标数目的增加,SPEA2+的收敛性更好。ε-MOEA尤其在混合的非连续性问题DTLZ7上表现最佳。虽然MOEA/D已经收敛,但是由于weight sum聚合函数的使用,算法的分布性不好,导致综合性能表现不佳。AR是一个高维多目标优化算法,其不适用于解决低维问题。 解集可视化图能够直观地给出解集的收敛性,特别是分布均匀性和分布广泛性。图2给出了6种多目标进化算法在DTLZ3的3目标上的最优解集可视化图,该图坐标轴上的标示f1、f2和f3分别表示第一个、第二个和第三个目标。从图2中可以看出6个算法的解集都收敛在Pareto前沿面上。SPEA2+和SPEA2的分布性最好,最优解集均匀且广泛地分布在整个Pareto前沿面上。ε-MOEA的解集分布较均匀,但是某些区域没有解。NSGA-II的解集有重叠,且部分区域没有解。MOEA/D和AR的分布性最差,解集都集中在3个区域。 (a) AR (b) ε-MOEA (c) MOEA/D (d) NSGA-II (e) SPEA2 (f) SPEA2+ 图2 6种多目标进化算法在DTLZ2的 3目标上的解集可视图 本节分析6个多目标进化算法在ZDT系列5个测试问题上的IGD指标值,如表2所示。SPEA2+在5个测试用例上的综合性能均最好,比SPEA2稍好,因为在2目标优化问题上,Pareto支配关系能挑选出表现优秀的个体进入下一次迭代,所以分布性保持机制的优势并不明显。NSGA-II的综合性能稍差于NSGA-II,其他3个算法ε-MOEA、AR和MOEA/D效果一般。 表2 6个多目标进化算法在ZDT测试集上的IGD指标值 图3给出了6种多目标进化算法在ZDT1的2目标上的最优解集可视化图。可以看出6个算法获得的解集均收敛。SPEA2+和SPEA2的分布性很好,解集都均匀广泛地分布在整个Pareto前沿面上。其次是NSGA-II和ε-MOEA,它们分布都很广泛,但是不够均匀。MODA/D和AR在某些区域没有解分布。 (a) AR (b) ε-MOEA (c) MOEA/D (d) NSGA-II (e) SPEA2 (f) SPEA2+ 图3 6种多目标进化算法在ZDT1的 2目标上的解集可视图 本节分析6个多目标进化算法在雨水排放系统优化问题上的实验结果,采用IGD指标来评价算法进化后获得的最终解集的综合性能,如表3所示。SPEA2+在该实际应用问题上的综合性能最好,比经典的MOEA/D和SPEA2都好。从而可以验证,SPEA2+在带有约束的5目标测试问题上的综合性能并没有随着目标个数的增加而显著下降。 表3 6个多目标进化算法在雨水排放系统优化问题上的IGD指标值 在2目标的测试问题上,SPEA2+中的基于角度选择的分布性保持机制的在增加收敛压力方面的优势并不能完全体现出来。因此,将SPEA2+与SPEA2在DTLZ2测试问题的3目标和5目标上比较其收敛性,使用GD指标进行评价,如图4所示。S表示SPEA2,S*表示SPEA2+。横轴是运行的代数,纵轴是GD指标值。GD值越小越好。 图4 SPEA2+与SPEA2的收敛性比较 在3目标测试问题上,SPEA2+的收敛性稍优于SPEA2。当目标个数从3个增加到5个时,SPEA2+的收敛性明显优于SPEA2。因此可以证明SPEA2+中基于角度选择的分布性保持机制的在增加收敛性方面的有效性。 本文介绍了一种基于角度选择的第二代Pareto强度进化算法,此算法比SPEA2在收敛性方面更加有效,且同时能保持种群很好的分布性。将同时包含了个体的收敛性和分布性的角度信息引入了分布性保持机制,提出了一种基于角度选择的分布性保持机制。基于12个国际标准测试问题及一个带约束的高维实际应用问题,对比了本算法与其他5个经典的多目标进化算法,实验结果表明提出的算法在低维问题上具有很好的收敛性和分布性,具有很强的全局搜索能力,且在5目标问题上的综合性能仍然较好。 未来的工作可以在以下两方面展开:1) 将提出的基于角选择的分布性保持机制应用到高维多目标进化算法中;2) 将本文提出的算法应用于更多的实际工程问题,来验证算法的有效性。3 第二代Pareto强度进化算法
3.1 个体适应度赋值

3.2 修剪操作
3.3 环境选择
3.4 SPEA2
4 使用角度选择策略的第二代Pareto强度进化算法
5 时间复杂度分析
6 实验设计
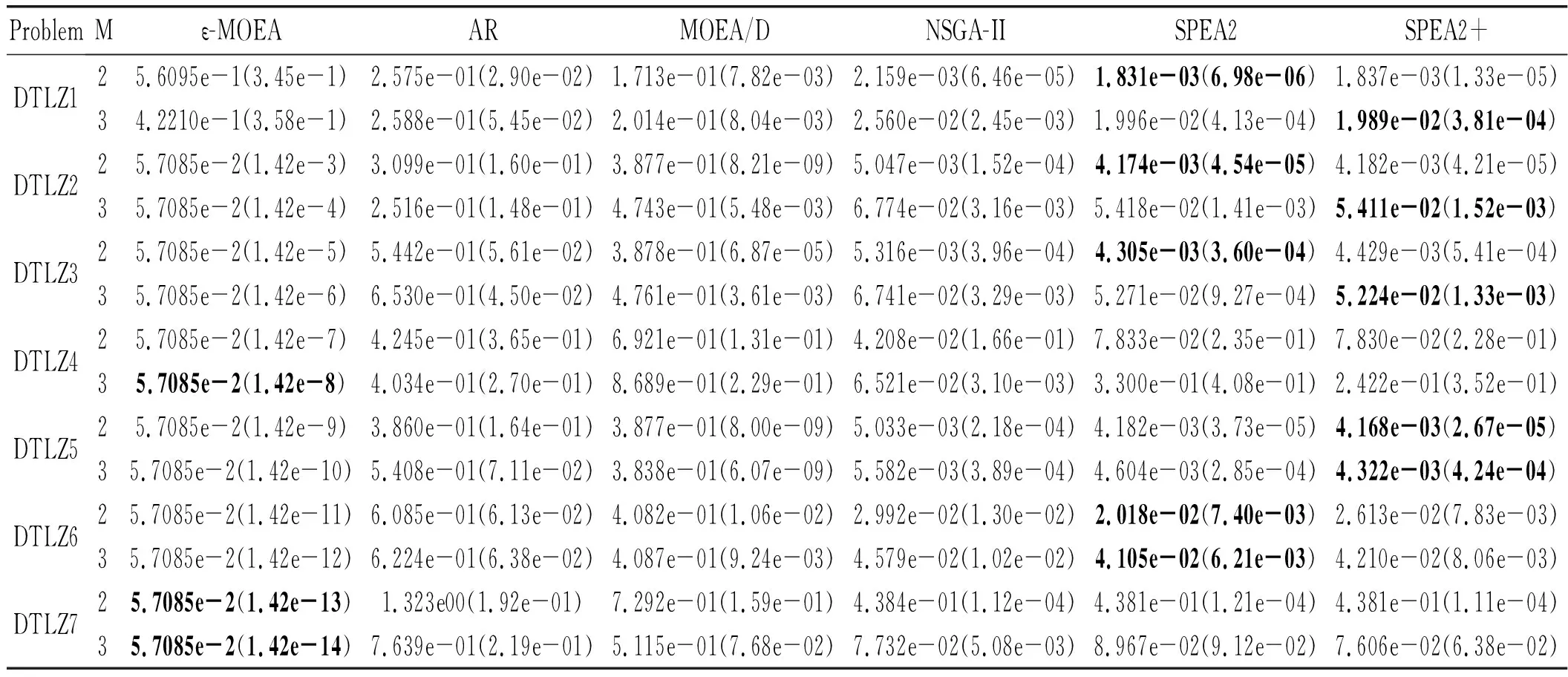
7 实验结果分析
7.1 DTLZ系列测试问题比较



7.2 ZDT系列测试问题比较

7.3 雨水排放系统优化问题的实验结果及分析

7.4 SPEA2+与SPEA2的收敛性比较
8 结 语
