OpenStack云平台的监控系统算法设计与实现
2018-07-25王志明
王 元,王志明
(1.南京邮电大学 通信与信息工程学院,江苏 南京 210003;2.南京工程学院 通信与信息工程学院,江苏 南京 211167)
0 引 言
监控作为管理云计算平台的重要举措之一,使得管理员能够获取系统运行的信息,从而调整自己的行为,提供更高的服务质量[1-4]。开源云平台OpenStack有多个物理节点,不同物理节点之间在传输数据时会消耗一定的带宽。而监控作为一种管理手段,不应该消耗过多的带宽资源。因此,在OpenStack云平台中构建合理的监控系统,该系统具有一定的预测能力,也就是说能够预测下一时刻的数据,这样可以减少物理节点之间的数据传输[5]。然而,监控系统的预测能力,即预测准确性,是至关重要的,同样也是一个难点。
在OpenStack云平台提供的Ceilometer项目的基础上[6-8],设计并实现了一个监控系统,该系统通过在不同时刻采用不同的预测算法,从而更加准确地预测下一时刻的资源状态。
1 基本的预测算法
近年来,国内外有很多学者都在研究云平台中的预测算法,通过预测算法对下一时刻的数据进行监测。文献[9]提出一种使用马尔可夫链模型(Markov chain model,MCM)来预测监测时间间隔(MTI)的监测机制,基于预测状态和作业处理时间,调整监视时间间隔。文献[10]提出一种基于时间序列的预测技术,自适应动态调整数据采集的时间间隔。从历史数据中学习,找到规律、数据的特征,以一定的可信度预测未来事件。
1.1 线性回归分析
线性回归分析预测是一种通过分析自变量和因变量之间的关系,构建变量间的线性回归方程,通过该方程根据自变量的变化来预测因变量值的预测算法[11-12]。
OpenStack云平台中的内存利用率如表1所示。
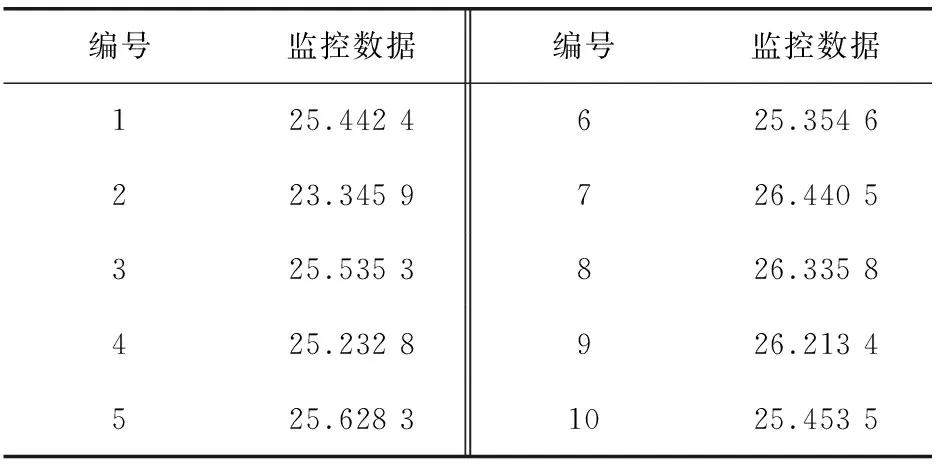
表1 内存利用率
将表1中的前五个数据作为训练数据,后五个作为预测数据。在使用线性回归算法进行预测时,得到的直线方程为y=25.267 84。预测后五个数据,若误差容忍度为1,命中率为20%。预测结果见表2。

表2 线性回归算法预测
线性回归算法预测的结果呈正相关关系,可以在一定程序上预测数据,但是无法保证其精度。由于其直线的特性,对于某些变动比较大的数据,不能进行准确预测。因此,线性回归无法适应于要求比较严格的系统。
1.2 马尔可夫预测
马尔可夫预测法是一种预测事件发生概率的方法,不仅能列出事件发生的各种可能结果,还给出了每一种结果发生的概率,即事件在预测期内出现该种结果的可能性程度。在马尔可夫链模型中,事件在任何时间发生的概率是先前时间段发生的事件的概率函数[13]。
使用离散时间马尔可夫链算法[14]对表1中的数据进行建模预测,状态划分情况如表3所示(转移矩阵的每个状态所表示的区间宽度为1)。预测后五个数据,当ETD=1时,命中率为50%。另外,由于在29这个状态上没有训练数据,根据算法设定预测值是它自己的状态。(注:如果预测失败,小括号里的表示调整后的状态)
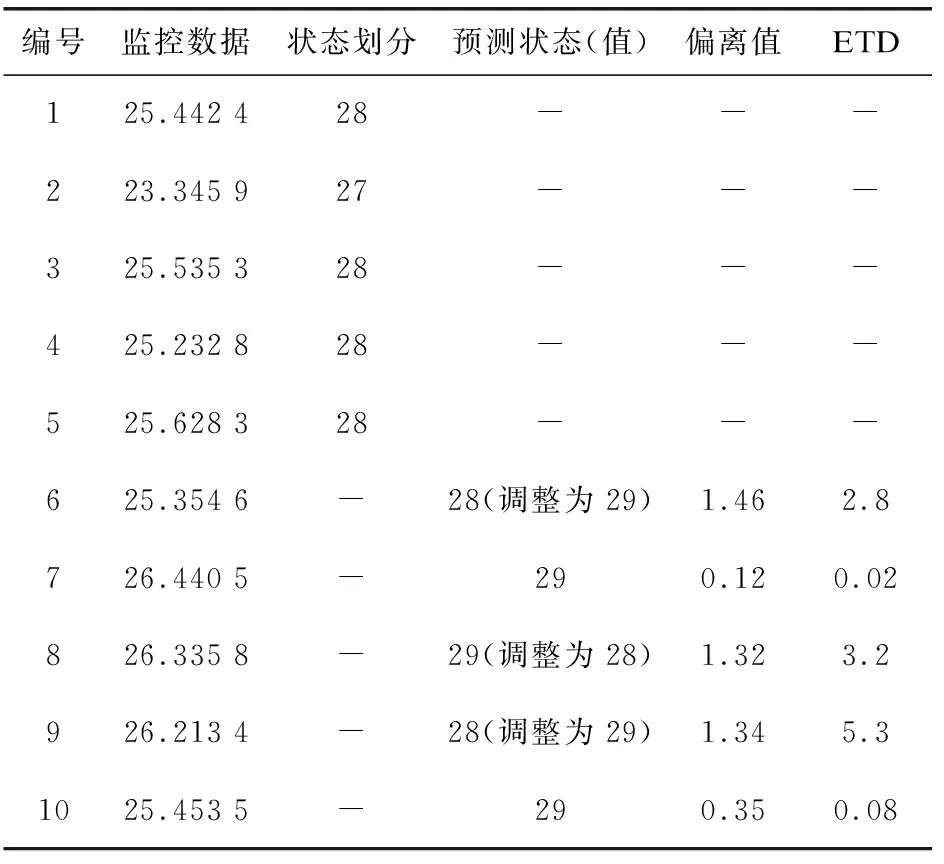
表3 DTMC算法状态划分以及预测
从表3可看出,DTMC预测算法的状态划分对预测的命中率起着决定性作用,五个测试数据相差都不大,如果状态划分的分割点是26.440 5,命中率则达到70%。由此可看出,仅仅是因为状态划分的问题而造成的命中率只有40%。一个好的划分不但能提高DTMC算法预测的命中率,而且还能降低算法的开销。然而在云计算环境中,数据是经常变化的,一个固定不变的划分会大大降低云计算环境中资源监控数据的命中率。
2 混合算法的设计和实现
上一节介绍了线性回归算法和DTMC算法并指出了它们在预测云计算监控数据上的缺陷,本节提出基于回归和DTMC的混合算法L-D,对云计算环境的监控数据进行预测。
在云平台环境中,虚拟系统对平台资源的消耗和时间有很大关系,符合“潮汐”规律[15]。在高峰时间段内,资源消耗呈无规律变化,因此监控系统收集到的数据也是不稳定的,此时可以分成不同的时间段应用不同的预测算法进行解决。在系统比较繁忙的时候,采用马尔可夫链预测算法对数据进行预测,而在其他时间段则采用线性回归算法进行预测。算法流程如下:
(1)判断ti是否处于系统繁忙时期,如果是,则按照马尔可夫链方法进行处理,构建转移概率矩阵;如果不是,则按照线性回归处理。
(2)建立直线方程y=mean。
(3)使用直线方程y,计算{ti}与y的偏离值序列{tic}。
(4)根据{tic}以及精度要求分配状态,数据如表4所示。当精度要求为1,直线y=25.241 3,TH=10时,数据被划分为(-5,-2),[-2,-1),[-1,0),[0,1),[1,2),[2,5)。其中,当偏离程度超过5时,则需要重新开始计算直线方程。表4中,前五个数据是有效的(与直线的偏离值在TH范围内),后五个数据是无效的(因为只有一个数据值与直线的偏离值在TH范围内)。

表4 内存利用率及状态划分
(5)计算状态转移矩阵P,矩阵中第i行第j列的元素表示在训练数据中从状态i经一步转移到状态j的总次数,依据表4得出矩阵P:

(6)预测,根据系统当前时间决定使用哪个预测模型。如果是忙碌时间,则使用矩阵R进行预测;否则,选取合适的直线方程以及矩阵R2进行预测。当从状态i转移出去时,在第i行中选择最有可能的下一个状态(第i行中值最大的那一列)作为预测状态。如i=3时,最有可能的下一个状态是3,即留在原地。
(7)计算预测值,在选择好状态后,选择该状态所表示的区间的中点作为预测偏离值v(此处v=0.5)。
(8)计算最终预测值,根据使用的预测模型计算预测值,如果使用矩阵R进行预测,最终的预测值则是该状态所表示的值区间的中位数;否则最终的预测值是该状态所表示的值区间的中位数加上直线y的值。最终预测值为y+v(28.769 34),y是直线方程(y=25.241 3)。
当使用L-D算法对表1的数据进行建模预测时,得出直线方程y=28.269 34。然后根据计算得到的训练数据与直线的偏离值划分状态,构建马尔可夫转移概率矩阵(TH=10时,数据被划分为(-10,-1),[-1,0),[0,1),[1,10),状态用0,1,2,3分别表示)。如表5所示,当ETD=1时,命中率为80%。(注:如果预测失败,小括号里表示调整后的状态)

表5 L-D算法状态划分以及预测
L-D算法的马尔可夫矩阵的状态空间虽然是固定的,但是通过相同的状态来预测不同时刻的数据值不一定是相同的,它随着直线的变化而变动。表5中马尔可夫矩阵的状态2表示的预测值是28.769 34,在未来某时刻,该状态表示的预测值可能是58.634 2,它是根据直线方程变化的,而不是固定不变的。相比DTMC算法,L-D算法这种特性,在平台突发性事件发生时(如虚拟机新建),无需担心新的数据范围未得到训练而需要重新训练模型,只需要调整直线方程即可,提高了预测的命中率。
3 测试过程和结果分析
文中部署了OpenStack云平台,根据用户设置的阈值,分别采用线性回归预测算法、马尔可夫链算法和混合算法对系统中的数据进行预测。如果实际的数据在设定好的阈值内,表明预测算法准确性高,因此可以丢弃该数据,避免数据传输。如果在阈值之外,则节点需要将数据传输到其他节点上,从而进行数据更新。
实验使用内存和磁盘利用率来评估预测算法的性能。数据一致性测试结果如表6所示。

表6 数据的一致性测试
由表6可知,在三种算法中,混合算法比另外两种预测算法能够更加精确地预测下一时刻的数据,避免了不必要的网络传输,降低了网络资源的消耗。
4 结束语
分析和研究了云计算中的监控系统,提出在不同时间段采用不同的预测算法模型,即在高峰时采用马尔可夫链算法,其他时间段采用线性回归算法对系统进行监控预测。实验结果表明,该算法的预测命中率更高,更能降低网络传输开销。
