改进的强跟踪求积分卡尔曼滤波算法
2018-07-25贺姗,赵旭,师昕
贺 姗,赵 旭,师 昕
(西安工程大学 计算机科学学院,陕西 西安 710048)
1 概 述
针对目标跟踪系统[1-3]中的状态估计问题,卡尔曼滤波(Kalman filter,KF)[4]是一种线性最优滤波算法。针对非线性高斯系统滤波问题,在实际应用中通常采用扩展卡尔曼滤波(extended Kalman filter,EKF)[5-6],滤波过程通过对系统的非线性状态方程或量测方程进行泰勒级数展开,并截取展开式的前一阶或者二阶项,即可将系统非线性方程变换成线性方程,从而滤波过程可以使用卡尔曼滤波。扩展卡尔曼滤波算法具有较高的运算速度,因此在解决非线性系统滤波问题时人们通常会采用该算法。然而,该算法在对非线性方程进行线性化近似时存在截断误差,尤其是对于强非线性系统,滤波过程较易产生扩散。
为使得非线性系统的滤波性能得到进一步提高,Gordon等提出了粒子滤波算法(particle filter,PF)[7-8]。PF是一种贝叶斯最优滤波和Monte Carlo随机采样方法相结合的统计滤波算法,适用于任意非线性、非高斯系统,且其滤波精度可以逼近最优估计,是一种非常有效的非线性滤波算法,但是其主要缺点是计算时间复杂度会随着状态变量维数的增加而迅速增大。随后,为了处理非线性滤波问题时能够获得较高的精度以及较快的计算速度,Julier等在不敏变换(unscented transformation,UT)的基础上提出了不敏卡尔曼滤波(unscented Kalman filter,UKF)[9-10]。UT变换通过采样策略选取一系列的西格玛点集,并用这些西格玛点集近似系统状态分布的均值和方差,理论上其精度可以达到二阶。同时,该算法不需要计算非线性函数的雅克比矩阵,因此也得到了广泛的应用。但是,当系统的维数超过三阶时,该算法的滤波精度会随着系统维数的增加而降低。2007年,Arasaratnam等在高斯厄米特滤波的基础上提出了一种新的非线性滤波算法-求积分卡尔曼滤波(quadrature Kalman filtering,QKF)[11-13]。该算法是利用高斯-厄米特积分准则来计算非线性系统的概率密度,能够取得较好的滤波精度。
然而,上述非线性滤波算法对于系统模型都具有严格的要求,系统模型的不确定性,包括建模不准确、模型状态简化以及实际系统模型参数变动等,滤波过程如果直接采用标准的非线性滤波算法,都会使得系统的状态估计值偏离真实状态值,导致滤波过程发散,滤波精度降低。为了克服系统模型不确定的鲁棒性,周东华等提出了强跟踪滤波器(strong tracking filter,STF)[14-16],该算法在应对系统状态突变问题时具有较好的跟踪能力和抗干扰能力。基于此,将强跟踪滤波算法思想引入到非线性滤波算法中,从而得到了几种相应的强跟踪非线性滤波算法,包括强跟踪扩展卡尔曼滤波算法(strong tracking extended Kalman filter,SEKF)[17]、强跟踪不敏卡尔曼滤波算法(strong tracking unscented Kalman filter,SUKF)[18]、强跟踪粒子滤波算法(strong tracking particle Kalman filter,SPF)[19]以及强跟踪求积分卡尔曼滤波算法(strong tracking quadrature Kalman filter,SQKF)[20]等。
上述强跟踪非线性滤波算法的主要思想是将渐消因子引入状态预测协方差阵中,能够在线实时调整增益矩阵,从而强迫当前时刻输出的残差序列能够保持正交,那么在系统模型不确定的情况下,上述算法均能保持对系统状态的良好跟踪能力。但是由于强跟踪滤波算法实现过程中对判断滤波发散的阈值设置较小,即使在系统正常情况下也会产生渐消因子,导致过度调节滤波增益,造成系统状态估计不够平滑,滤波精度降低。针对上述问题,文献[21]对强跟踪滤波算法进行了改进,提出了一种改进的强跟踪滤波算法(improved strong tracking Kalman filter,ISTF)。该算法的主要思想是在滤波过程中通过增大判断滤波发散的阈值,从而有效降低了误判滤波发散的概率,提高了滤波器对于系统状态的跟踪性能,获得了更高的滤波精度。
为了能够改善强跟踪求积分卡尔曼滤波算法的滤波性能,借鉴文献[21]的思想,文中提出了一种改进的强跟踪求积分卡尔曼滤波算法(improved strong tracking quadrature Kalman filter,ISQKF),并进行了仿真验证。
2 强跟踪求积分卡尔曼滤波
考虑如下的非线性系统模型,状态方程和量测方程分别为:
xk=f(xk-1,uk-1)+wk-1
(1)
zk=h(xk)+vk
(2)
其中,xk∈n表示状态变量;uk∈n表示控制变量;zk∈n表示观测向量;wk-1和vk分别为互不相关的零均值过程噪声和量测噪声,其方差分别为Qk和Rk。
强跟踪求积分卡尔曼滤波算法的主要思想是在状态预测协方差阵中引入渐消因子λ(0≤λ≤1),在线实时调整增益矩阵Wk,强行使输出的残差序列保持正交,最大限度地提取残差序列中的一切有效信息,从而提高滤波器的跟踪性能。当系统模型和真实系统匹配度较高时,渐消因子λ趋近于1,此时,强跟踪求积分卡尔曼滤波算法将会退化为标准求积分卡尔曼滤波算法,不会影响到系统状态估计的结果。而当系统模型不确定时,λ的取值将趋近于0,此时,强跟踪算法能够削弱前一刻的数据对于当前时刻滤波结果的影响,从而减弱系统模型不确定所带来的影响,这样强跟踪求积分卡尔曼滤波算法在模型不确定时仍然能够具有较强的跟踪性能。
强跟踪求积分卡尔曼滤波算法具体的实现步骤如下:
状态更新:
(3)
(4)
(5)
(6)
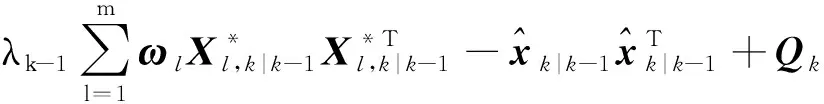
(7)
量测更新:
(8)
(9)
Zl,k|k-1=h(Xl,k|k-1,uk,k)
(10)
(11)
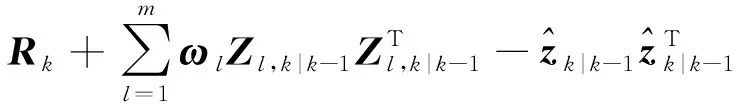
(12)
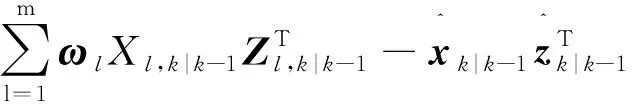
(13)
(14)
(15)
(16)
其中
(17)
(18)
其中
(19)
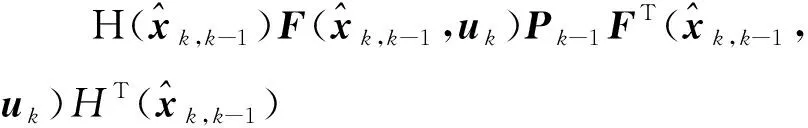
(20)
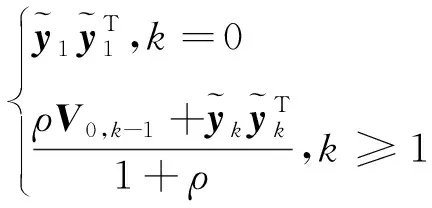
(21)

3 改进的强跟踪求积分卡尔曼滤波算法
针对非线性滤波问题,强跟踪求积分卡尔曼滤波算法主要思想是将渐消因子λk-1引入到状态预测协方差阵Pk|k-1中,在线实时调整增益矩阵Wk,从而使输出残差序列保持正交,这样强跟踪求积分卡尔曼滤波算法在应对模型不确定时仍然能够保持对系统状态的良好跟踪性能。然而,在实际应用中发现,强跟踪求积分卡尔曼滤波算法在应对系统状态突变问题时会出现滤波精度降低的问题,导致滤波精度降低的主要原因是由于在求解V0,k时得不到解析解,而只能通过参差序列获得其近似值,从而导致其近似值与理论值出现了偏差,使得对系统状态估计不够平滑。强跟踪求积分卡尔曼滤波算法问题分析如下:
k时刻V0,k的理论值C0,k可通过下式求得:
(22)
V0,k的近似值可通过式21求得:
(23)
其中,yk~N(0,C0,k),那么k时刻的残差yk可以认为是对高斯分布N(yk;0,C0,k)的一次采样,那么可得到:
(24)
相应滤波发散的概率为:
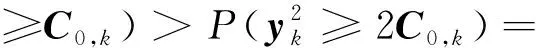
1-84.1%≈16%
(25)
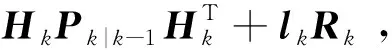
为了解决上述问题,提出了一种新的滤波算法即改进的强跟踪求积分卡尔曼滤波算法。该算法的主要思想是在算法实现过程中适当增大判断滤波发散的阈值,从而有效降低了误判滤波发散的概率,大大减小了产生渐消因子的概率,并能够根据不同维数的量测方程确定弱化因子的取值。
由于
(26)
则
(27)
因此,可将判定滤波发散的阈值提高到3C0,k,则
(28)
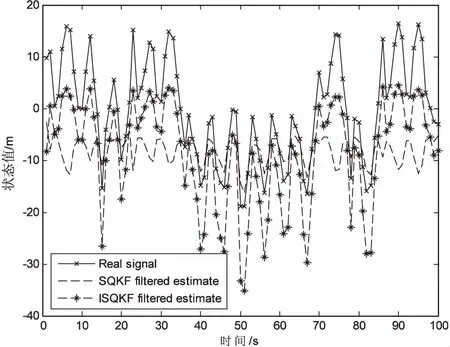
即使考虑V0,k的影响,由于V0,k (29) 因此,当把V0,k的值取到3C0,k时,滤波发散的概率仅为1.5%~2.6%,新算法滤波发散的概率远远小于强跟踪求积分卡尔曼滤波算法滤波发散的概率。 那么,当V0,k=3C0,k时,则有: (30) 由上式可得: (31) 那么改进的强跟踪滤波算法的渐消因子即为: (32) (33) 其中 (34) (35) 上述改进的强跟踪求积分卡尔曼滤波算法的推导是针对一维系统,若要推广到多维系统中,那么判断滤波发散的条件为: (36) 假设V0,k和C0,k两者相等,上式可改写为: Tr(V0,k)≥Tr(l'C0,k) (37) (38) 其中,n为量测方程的维数。 (39) 那么,针对非线性滤波问题,当采用文中提出的ISQKF时,即可通过式39确定弱化因子的取值,从而避免了凭经验选取弱化因子的问题。 单变量非稳定增长模型(univariate nonstationary growth model,UNGM)如下: (40) (41) 其中,α=0.5,β=25,γ=8。 设该系统的初始值分别为:x0=0.1,P0=0.1以及N=100。根据式39可知弱化因子l'=3。 由式40和式41可知该系统为非线性系统,滤波过程中分别采用SQKF以及提出的ISQKF进行滤波估计。 实验仿真结果如图1和图2所示。 图1 SQKF与ISQKF状态估计结果对比 图2 SQKF与ISQKF估计误差对比 由图1可知,经过ISQKF滤波后的状态估计值与SQKF滤波后的状态估计值相比更加趋近系统真实状态值。由图2可知,采用ISQKF滤波后的滤波误差明显小于SQKF滤波后的滤波误差。综上所述,针对系统不确定问题,提出的ISQKF与原有的SQKF相比,具有更高的滤波精度,状态估计值更加接近于系统真实值。 对于非线性高斯系统,强跟踪求积分卡尔曼滤波算法在实现的过程中由于存在对判断滤波发散的阈值设置较小的问题,从而使得误判滤波发散的概率增大,进而增大了产生渐消因子的概率,造成过度调整滤波增益,最终导致对系统状态估计出现较大偏差。为了解决上述问题,提出了一种改进的强跟踪求积分卡尔曼滤波算法。该算法主要通过增大判断滤波发散的阈值,从而有效降低了误判滤波发散的概率,增强了滤波器对系统状态的跟踪性能,获得了更高的滤波精度,并能够根据不同维数的量测方程确定弱化因子的取值,从而避免了凭经验选取弱化因子,具有较强的操作性。对两种算法进行实验仿真,结果表明,改进算法具有更高的滤波精度,减小了系统状态估计值与真实值之间的偏差。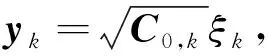


4 仿真实验及结果分析

5 结束语
