一种障碍空间中移动对象的连续k最近邻查询方法

万静 唐贝贝 何云斌 李松

摘 要：针对时空数据库中的连续移动对象的最近邻查询问题，提出COpKNN（continuous obstructed possible k-nearest neighbor）查询：在二维空间中，给定一个移动查询点q、一组移动查询对象集合P和一组多边形障碍物集合O，根据障碍距离的概念，查询q所有可能的k最近邻集合。由于移动对象本身的不确定性以及现实生活中障碍物的存在，已有的查询方式不再适用COpKNN查询。COpKNN查询包括三个子过程：根据可视图、R树和堆排序的概念，给出计算两点之间障碍距离（大于等于欧几里得距离）的方法；基于R树的查询方式查找在用户给定时间段内q所有可能的k最近邻结果集（初步结果，也叫候选集）；采用Mindist（E，q）和候选集更新算法UpdataC（pn）对k最近邻结果集进行剪枝，得到较为精确的k最近邻结果集。实验数据集和障碍物集均采用真实的数据集，理论研究和实验结果表明，该方法具有良好的效率。

关键词：R树；k最近邻查询；不确定性；可视性；障碍距离

DOI：10.15938/j.jhust.2018.03.008

中图分类号： TP311.13

文献标志码： A

文章编号： 1007-2683（2018）03-0044-07

A Continuous k-Nearest Neighbor Query Method

for Moving Data in Obstructed Spaces

WAN Jing， TANG Bei-bei， HE Yun-bin， LI Song

（School of Computer Science and Technology，Harbin University of Science and Technology，Harbin 150080，China）

Abstract：To solve the nearest neighbor query of continuously moving objects in Spatio-temporal database， we study novel form of continuous k-nearest neighbor query in the presence of obstacles， namely continuous obstructed possible k- nearest neighbor （COpKNN） search. Given a data set P， an obstacle set O， and a query point q in a two-dimensional space， a COpKNN query retrieves all possible k-nearest neighbors of each point on q according to the obstructed distance. Duo to the inherent of moving data objects and the existence of obstacles in our real life， previous techniques to answer nearest neighbor （NN） query cannot be directly applied to the COpKNN problem. The P COpKNN query method mainly includes three sub-algorithms： according to the concept of Visibility graph， R-tree and Heap Sort，given the method of calculation of the obstacle distance（greater than or equal Euclidean distance） between two points； find all possible k-nearest neighbors of q between user given time period based on R-tree； Using Mindist （E，q） and the candidate set update algorithm UpdataC （pn） to prune kNNs to get the correct k-nearest neighbors. Experimental data sets and obstacle sets are all based on real data sets，theoretical and experimental results show that the method with good efficiency mentioned herein.

Keywords：R-tree； k-nearest neighbor query； uncertainty； visibility； obstructed distance

0 引 言

最近邻（nearest neighbor，NN）查询是LBS（location based servies）众多查询类型和处理方法中一种最常用的查询方式[1]，且随着智能移动设备（如PAD、智能手机）的普及和无线通讯以及定位技术（如GPS）的快速增长，越来越多的用户在他们移动的时候发出查询请求，移动对象的动态查询也迅速发展。然而，最近邻的研究大多数是不考虑障碍物以及查询对象移动的不确定性。MR Kolahdouzan等[2]提出时空网络数据库中的两种CKNN查询IE和UBD；YK Huang等[3]提出CPKNN（continuous possible KNN）查詢；A. Prasad Sistla等[4]研究了确定位置的连续KNN查询以及不确定位置的连续KNN查询，分别对两种查询进行在线和不在线两种方式进行研究。国内在空间和时空数据库最近邻查询处理技术方向的研究也取得了较为丰硕的成果。孙冬璞等[5]研究了移动对象历史轨迹的连续最近邻查询；黄敬良等[6]提出基于TPR树的移动对象的K个连续最近邻查询，在该文献中提出了分界时间的概念；刘斌，万静[7]提出了基于R树的连续最近邻查询算法优化研究；袁培森等[8]研究了一种基于学习的高维数据c-近似最近邻查询算法。

但以上算法都是基于理想的欧氏空间的。在障碍空间中，不能单纯的以欧几里得距离计算查询点和查询对象之间的距离。李松等[9]提出了障碍物环境下的单纯型连续近邻链查询；张丽萍等[10]提出了基于Voronoi图的障碍物环境下的单纯型连续近邻链查询；Yunjun Gao等[11]提出了障碍空间下的CONN（continuous obstructed NN）查询。上述算法中没有考虑到查询对象本身的不确定性。然而，不确定性是管理移动对象位置信息的时空数据库的固有属性。由于测量的不精确性、连续运动本身的不确定性以及网络延迟的因素，移动对象存储在数据库中的位置信息并不能总是精确地表示它们的真实位置。甚至在有的场景中，位置的不确定性是人为引入的。例如，为了保护基于服务的位置隐私性，不确定性被注入到用户的位置信息中[12]。如文[13]给出了基于位置不确定性的k最近邻（kNNs）查询；文[4]也给出了相关不确定性查询；文[14]提出了基于不确定Voronoi图的概率性查询，也给出了不确定性的相关查询。

综合以上论述，已有的最近邻研究方法中，针对移动对象本身的不确定性上的研究有所不足，且现有kNN查询大都只查询要求的k个对象，而实际上只要在第k个最近邻的相同范围内，可能会有大于等于k个对象。所以为了解决这些问题，进一步提高查询性能，本文研究一种空间COpKNN（continuous obstructed possible kNN）查询：给定一个移动查询点、一组移动查询对象集合和一组多边形障碍物集合（为了描述方便，本文障碍物定义为多边形和线段），根据最短路径度量dist_O（dist_O是指障碍距离，两点之间最短避障路径的长度）采用R树索引结构对移动目标进行索引，找到所有可能成为查询点的kNNs的移动对象，并且树的每个节点只被访问一次。

1 问题定义

1.1 基本定义

本节中主要定义COPKNN（continuous obstructed possible k-nearest Neighbor）查询，以及与COPKNN查询相关的概念定义，且本文中任意两可见点之间的距离均采用欧几里得度量方法计算，两点间的距离用dist_euc（）表示，障碍距离均用dist_o（）。

定义1 （k最近邻查询[15]） 给定查询点q和查询对象集P={p1，p2，…，pn}，k最近邻查询就是检索任意p∈P，满足dist（q，p）≤dist（q，pk）。即：kNN（q，P）={p1，p2，…，pk}，其中，p∈P-kNN（q，P），dist（q，p） ≤max{p∈kNN（q，P）|dist（q，p）}。

在定义1中，dist（）表示两点之间的最短距离函数；pk∈P且pk是根据最短距离函数dist（）计算的q的第k个最近邻点。

定义2 （点与点的可视性[16]）给定点p，p ∈P和障碍物集O，p和p可视当且仅当它们之间没有任何障碍物阻挡，即o∈O，[p，p] ∩o=。

定义3 （最短障碍距离[1]）在数据点集P={p1，p2，…，pn}中，存在障碍物集O={o1，o2，…，om}。任意两点p1，p2∈P。那么p1，p2之间的最短障碍距离

dist_O（p1，p2）=min{（∑n-1k=1dist_euc（vk，vk+1）+|pi，v1|+|pj，vn-1|}。

在定义3中，点vk，vk+1为任意两可见点，n为可见点总数。即直线段vkvk+1不与O中任意障碍物相交，dist_euc（vk，vk+1）表示线段vkvk+1的欧几里得距离长度。

定义4 （障碍最近邻ONN查询[17]）。给定一个数据集P，障碍集O和查询点q。ONN（q）={ p∈P|pi∈P- {p}：dist_o（p，q） ≤dist_o（pi，q）}。

定义5 （COpKNN）给定一个查询点q，查询对象集合P={p1，p2，…，pn}以及障碍物集合O={o1，o2，…，om}。COpKNN查询结果返回所有可能距离查询点q最近的查询对象，所以COpKNN（q，k）={p1，p2，…，pk，…ps∈P|p∈P-{p1，p2，…，pk，…ps}， dist_o （p， q） ≥max1≤i≤s dist_o （pi， q）}。

1.2 主存障碍路径查询

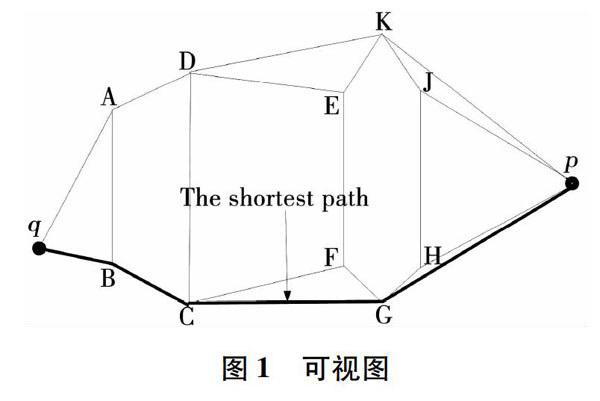
最短路径查询可以基于可视图[18]进行。可视图中的节点由所有障碍物的顶点和点q、p组成，可视图的边由任意两可视点的连线构成，如图1所示。图1中的粗线代表q与p之间的最短障碍距离。

引理1[19] 假定B一组多边形障碍物集合，点q与p之间的最短路径在于B和{q，p}组成的可见图。

在文[19]中，该引理表示点q与p之间可以有无限多条路径，它依然证明最短的那条定是存在G中的其中一条路径。最短路径计算方法分为两个步骤[17]，首先构造可视图，然后利用Dijkstra算法搜索G中的最短路径。第一步利用平面扫描[20]的方法需要O（n2logn）时间，用输出敏感算法[21]可以优化到O（l+nlogn）时间，其中l是G的边的个数。第二步利用Dijkstra算法需要O（m+nlogn）时间，其中m是G中边的个数，n是G中頂点的个数。

2 障碍空间中移动对象的连续k最近邻查询

本节提出障碍空间中连续移动对象的k最近邻查询的处理方法。由于移动对象本身的不确定性，首先定义移动对象的不确定区域；然后通过可视图和R树索引以及堆排序的概念，计算两点之间的最短障碍距离；以最短障碍距离为基准，通过R树索引查询q的所有可能的k最近邻集合；采用Mindist（E，q）和候选集更新算法UpdateC（pn）完成剪枝过程，得到最终结果。

2.1 不确定查询区域

本节假设查询点和查询对象均是连续移动的。每一个移动对象会不时向数据库发送更新，更新包括该对象当前的位置和速度矢量。在下一次更新之前，数据库会按照上次更新的结果假设移动对象的运动主区域。数据库上次更新结果如图2所示，查询对象起始运动点分别是圆环R1、R2对应的圆心位置，运动方向是Θ1、Θ2箭头对应的方向。

在用户给定的时间段（ts-te）内查询任一时刻查询点的k最近邻（kNNs），且移动对象的速度大小以及运动方向是不确定的。那么假设移动对象的速度大小在最大值和最小值之间，运动方向是任意方向，下面提出移动对象的可能区域模型以及计算距离不确定查询点可能区域最近的不确定对象集的算法。

移动对象o的可能区域Ro（t）随着时间在不断移动，Ro（t）的模型一个圆环，内环对应查询对象的最小速度在数据库下次更新之前所达到的位置，外环对应查询对象的最大速度在数据库下次更新之前所达到的位置，运动方向是圆环内的任意方向。Ro（t）如图2所示。

图2表示了具有不确定移动速度和移动方向的移动对象CPKNN查询的一个例子。图中O1O2代表障碍物，查询对象P1和P2的初始位置分别位于圆环R1和R2的圆心位置，且二者均具有不确定的移动速度，速度范围在圆环内环和外环之间，内环半径分别为|rp1|和|rp2|，外环半径分别为|rp1|和|rp2|外环与内环的半径差为rp。那么，在该时刻P1和P2的位置如图2所示，显然在该时刻查询点q的1NN是P1，且最近距离dist（q，p1）min=dist（q，O1）+dist（q，O2），易知dist（q，p2）> dist（q，p1）min。

為了提高查询效率，可根据上次数据库更新的结果确定查询的主区域，而不需要整个圆环作为查询区域。如图2所示，上次数据库更新的运动方向为Θ1、Θ2箭头对应的方向，那么在下次数据库更新时，二者的运动区域的概率最大值分别在a1b1d1c1、a2b2d2c2两个区域。这样移动对象就只需在a1b1d1c1、a2b2d2c2两个区域内确定，提高了查询效率。

2.2 查询对象候选集更新

由于障碍距离的计算代价比较昂贵，所以我们可以对查询对象进行筛选，只计算最有希望的对象集合（即候选集）。通过对查询对象候选集的选择，可以在用户给定的范围和时间段内快速的对一组查询对象进行k最近邻查询。尽管障碍距离和欧几里得距离不同，但二者是相关的，显然dist_O（p， q）≥dist_euc（p， q）。

算法核心思想：候选集更新算法既可判断新加入对象pn是否属于候选集Cn也是剪枝算法。当有新的对象pn加入查询对象集P时，首先根据新加入对象pn到查询点的欧几里得距离是否小于等于候选集中第n个对象到查询点q的障碍距离，如果是，则把pn加入候选集Cn，再次判断如果候选集Cn中任意一个对象p到查询点q的最小障碍距离大于rmax（rmax是候选集中第n个对象到查询点q的障碍距离），则p不可能是q的最近邻，否则p属于候选集Cn。作为剪枝算法直接判断候选集Cn中任意一个对象p到查询点q的最小障碍距离是否大于rmax，原理同上。

算法1 候选集更新UpdataC（pn）

输入：查询点q，障碍物R树Tobs，新加入对象pn

输出：候选集Cn

for i=1 to n ；

rmax←C[n]. dist_O；

while Cn≠；

if rmax≥dist_euc （pn，q） ；

Cn←Cn+{pn} ；

for p∈Cn；

if dist_O（p，q）+ rp+rq

≤rmax- rp-rq ；

Cn←Cn+{ p}；

return Cn.

定理1 算法UpdataC（pn）是正确的、可终止的，其时间复杂度为O（n）。

证明：（正确性）UpdataC（pn）算法采用Cn存放候选集，若查询对象集是不为空，且判断候选集中到查询点的最大障碍距离大于等于查询对象集中的查询对象到查询点的欧几里得距离，那么如果查询对象到查询点的障碍距离最大值小于等于候选集中到查询点的最大障碍距离最小值，那么该查询对象就属于候选集。依次循环，所以算法可有效选择候选集，是正确的。

（可终止性）UpdataC（pn）算法主要是while循环。而while循环中的Cn是有限集合。所以算法是可终止的。

（时间复杂度分析）算法中主要是while循环，假设Cn中有n个对象，那么while循环所需的时间为O（n）。所算法的时间复杂度为O（n）。

2.3 最短障碍距离计算算法

算法核心思想：算法主要利用R树、堆和可视图的概念进行最短路径计算。首先将障碍R树Tobs中未访问的结点放入堆H中，依次判断H中的结点是否为一个障碍物。若是且与p和点q之间的最短路径相交，则把该障碍物加入可视图，根据Dijkstra算法计算最短障碍路径，否则把该点插入H中，重复上述步骤。

算法2 障碍距离计算算法Cdist_O（q，p）

输入：查询点q，查询对象点p，障碍物R树Tobs

输出：点q与点p的障碍距离dist_O（q，p）

G←，H←，dist_O（q，p） ←∞ ；

从R树Tobs的根结点开始进行遍历；

将Tobs的根插入到H中；

while H≠Φ do

将H中的第一个元素（o，key）出堆；

if o是障碍物的一个MBR；

for oi∈o；

将（oi，mindist（oi，q））插入到H中；

elseifo是一个内部结点；

将（o，mindist（o，q））插入到H中；

else

if（o与q、p之间的最短路径相交）；

o∈Co；

if（Co=）；

return dist_euc（p，q）；

else

更新可视图G，将q、p、Co加入到G中；

dist_O（q，p）=Dijkstra（G，q，p）- rp- rq；

定理2 算法Cdist_O（q，p）是正确的、可终止的，其时间复杂度为O（|G|×log|G|×log|Tobs|+n），其中|G|为可视图中节点的个数，|Tobs|为障碍树的大小。

证明：（正确性）算法Cdist_O（q，p）将Tobs中未访问的结点存放在堆H中，结点按照与q之间的最短距离的升序存放，这里的距离指欧几里德距离。算法从根结点开始遍历R树，得到p和点q之间的障碍距离dist_O（p，q）。算法首先假设p和点q之间的最短路径距离为∞，对于小于该距离的元素（o，key），如果o是一个障碍，且与p和点q之间的最短路径相交，则o属于障碍物候选集Co，把Co加入可视图G中，利用Dijkstra算法重新计算最短路径距离；如果o是一个障碍物的MBR或者内部结点，则放入堆中继续计算。遍历R树之后，如果Co之外的障碍物o与p和点q之间的最短路径相交，那么把o加入Co中，更新G，重新计算最短路径距离。当障碍集中所有没有访问的节点的最小距离都大于当前障碍距离dist_O（p，q）时，算法得到最后结果。因此算法是正確的。

（可终止性）算法Cdist_O（q，p）中有while循环和for循环。而算法的while循环是针对H中的元素进行的，而H中元素的数量是有限的，另外for循环只和节点中元素个数有关是有限的，所以算法是可终止的。

（时间复杂度分析）算法的执行时间主要是遍历R树Tobs的时间、Dijkstra算法的执行时间和最后的for循环的时间。而Dijkstra算法的执行时间为（|G|×log|G|），遍历一次R树Tobs的时间为log|Tobs|，假设Co之外的障碍物的个数为n，则for循环的时间复杂度为O（n）。故Cdist_O（q，p）算法的时间复杂度为O（|G|×log|G|×log|Tobs|+ n）。

2.4 COpKNN算法

本小节介绍在一种障碍空间中，给出查询点q，查询对象集P，障碍物集O，在用户给定时间段内查询q所有可能的最近邻集合Pn，其中Pn内元素的个数可能大于k个。

算法核心思想：采用R树索引移动目标，通过深度优先遍历R树完成查询；采用Mindist（E，q）和候选集更新算法UpdateC（pn）完成剪枝过程；查询基于最短障碍距离进行，当最近邻结果集中的对象大于k个时，更新候选集上限rmax（即rmax等于当前查询对象的最短障碍距离），否则候选集上限不更新。

算法3 移动对象最近邻生成算法COpKNN（q）

输入：查询点q，k值，查询对象R树Tp，障碍物R树Tobs

输出：最近邻结果集Pn

Pn←，rmax←∞，n←0；

从Tp的根结点开始遍历；

for （p∈Tp） ；

if p是一个查询对象点 ；

if dist_O（p， q）≤rmax；

Pn←Pn+{p}；

n←n+1；

if n≤k and rmax≠∞；

rmax←rmax ；

else

rmax←dist_O（p，q） ；

UpdateC（pn）//更新候选集；

else

将查询对象的MBR根据Mindist（E，q）的升序排序，Mindist（E，q）最小值具有优先访问权；

for每一个MBR；

if dist_O（E， q）

对MBR内的结点进行判断，返回第4行。

定理3 算法COpKNN（q）是正确的、可终止的，其时间复杂度为O（log|Tp|），其中Tp为查询对象R树的大小。

证明：（正确性）算法COpKNN（q）首先设最近邻结果集为空，最近邻结果集上限为无穷大，然后从R树根结点开始向下逐层访问。如果访问结点是一个查询对象点，通过dist_O（p， q）≤rmax判断p是否为最近邻，若是更新结果集和rmax；如果不是查询对象点，将查询对象的MBR根据Mindist（E，q）的升序排序，Mindist（E，q）最小值具有优先访问权，根据dist_O（E， q）< rmax判断是否进入下一层查询，如果满足条件，访问下一层，返回算法第4行，直到查询到所有可能的最近邻结果集并完成剪枝。故该算法是正确的。

（可终止性）算法COpKNN（q）是针对Tp树进行遍历，而Tp树中的结点数是有限的。故算法COpKNN（q）是可终止的。

（时间复杂度分析）算法的执行时间主要是遍历R树Tp的时间，而遍历一次R树Tp的时间为log|Tp|。故算法的时间复杂度为O（（log|Tp|）。

3 实验结果与分析

在本节中，我们通过实验对本文提出的算法COpKNN进行性能评估。并与用基本方法（Basic）查询障碍空间中的kNNs（即不使用R树索引，查询每个查询对象到查询点q的障碍距离）以及与文[21]中的算法（MKNN算法）中的k值变化对性能的影响进行比较分析。为了方便比较，对实验算法细节进行了局部调整。试验运行环境为：1.70GHz Intel CoreTM i5-3317U CPU、4GB RAM、Windows7操作系统。障碍物集包含128971MBRs 的rivers①，为了尽可能符合现实中的情况，障碍物分布满足Zipf分布，其中Zipf分布的斜相关系数设为α=0.85。对象集包含98451MBRs的California数据流①，根据每个对象的运动速度（包括运动方向和速度大小）确定对象的不确定区域，且在该区域内服从高斯分布。查询点q随机从数据集中取出。每次的实验结果为执行100的平均值。

首先是k值对算法性能的影响。图3和图4分别给出了k值的变化对CPU时间和磁盘I/O代价的影响。其中CPU执行时间和I/O代价花费时间单位均为s。

由图3可以看出，k值从1变化到25的过程中，CPU时间随着k值的增加而增加。很明显，COpKNN方法的CPU时间增长率快于传统方法，是因为COpKNN方法剪枝过程中时间随k增长得比传统方法要快，而且两种方法的CPU时间差距明显。COpKNN方法和MKNN算法相比增长率不太明显，但和MKNN的CPU时间要少。实验结果表明本文提出的COpKNN方法要好于Basic方法和MKNN方法。

圖4给出了随着k值的增加对磁盘I/O代价的影响。Basic方法的磁盘I/O代价随着k值的增加而增加，MKNN方法和COpKNN方法的磁盘I/O代价随着k值的增加变化不太明显。由于k值越大，需要访问的数据点越多，磁盘I/O越大，而COpKNN方法仅需要访问离查询点较近的数据点，MKNN方法只需访问安全区域内的点，因此磁盘I/O代价要小很多。从图中可以看出，COpKNN方法要优于Basic方法和MKNN方法。

然后是数据点个数的影响。图5和图6分别给出了数据点密度对CPU时间和磁盘I/O代价的影响。其中CPU执行时间单位为s，数据点个数为×104。

由图5可见，随着访问数据点数量的增加， COpKNN方法所花费的CPU时间反而下降，而Basic方法的CPU用时是增加的。这是因为对于COpKNN方法，数据点越密集，查询点和它的障碍邻居之间越近，计算障碍距离的时候大多数不需要遍历可视图，只需要计算欧几里得距离。而Basic方法需要计算距离查询点较近的每个查询对象的障碍距离，因此对于Basic方法，数据点越多，CPU用时越多。

图6反映了随着访问数据点数量的增加，Basic方法的磁盘I/O代价随之增加，而COpKNN方法的磁盘I/O代价却是下降的。Basic方法需要计算距离查询点较近的每个查询对象，因而数据点越多，计算的数据点越多。而COpKNN方法，数据点越密集，需要访问的障碍物越少，因此不需要访问的数据点越多，所以COpKNN方法的磁盘I/O代价随着k值的增加反而减少。

最后障碍物个数的影响。图7和图8分别给出了障碍物个数对CPU时间和磁盘I/O代价的影响。其中CPU执行时间单位为s，障碍物个数为×104。

由图7可见，障碍物密度越大，CPU执行时间越多。障碍物个数越多，查询时需要访问的障碍物越多，CPU时间越大。而计算障碍距离要比计算欧氏距离用时更多， Basic方法需要计算距离查询点较近的每个查询对象的障碍距离， COpKNN方法只需计算部分障碍距离，因此它的CPU耗时更多。

图8给出了不同数量的障碍物对磁盘I/O代价的影响。随着障碍物个数的增加，两种方法的I/O代价都随之增加，但是COpKNN方法由于有效的剪枝策略极大地减少了障碍物的访问数量，因此磁盘I/O代价明显比Basic方法的代价少很多。

4 结 论

本文分析了现有kNN查询方法的不足，在此基础上对障碍空间中的移动对象的连续k最近邻进行了研究。随着智能移动设备、无线通讯技术、全球定位技术等的迅速发展，许多用户在他们移动的时候发出查询请求，这说明现实生活中的查询大多数不是在理想的欧氏空间中处理。所以，为了快速有效的对查询请求进行响应，本文提出了基于R树索引的障碍空间中移动对象连续k最近邻查询的方法。实验证明在一定情况下，COpKNN方法提高了障碍空间下移动对象的连续kNN查询效率。未来的研究重点主要集中在基于R树的不确定反向最近邻查询。

参 考 文 献：

[1] 李传文，谷峪，李芳芳，等. 一种障碍空间中不确定对象的连续最近邻查询方法[J].计算机学报，2010，33（8）：1359-1368.

[2] KOLAHDOUZAN MR，SHAHABI C. Continuous K Nearest Neighbor Queries in Spatial Network Databases[C].STDBM，2004，9（4）：33-40.

[3] HUANG YK，LIAO SJ，LEE C. Efficient Continuous K-nearest Neighbor Query Processing Over Moving Objects with Uncertain Speed and Direction[J]. Springer Berlin Heidelberg，2008，5069 （5）：549-557.

[4] SISTLA A. Prasad， WOLFSON Ouri， XU Bo. Continuous Nearest-neighbor Queries with Location Uncertainty[J]. The VLDB Journal，2015，24（1）：25-50.

[5] 孙冬璞，郝忠孝. 移动对象历史轨迹的连续最近邻查询算法[J].计算机工程，2009，35（1）：52-54.

[6] 黄敬良，郝忠孝. 移动对象的K个连续最近邻查询算法[J].哈尔滨理工大学学报，2007，12（6）：24-27.

[7] 刘彬，万静. 基于R-树的连续最近邻查询算法优[8] 袁培森，沙朝峰，王晓玲，等. 一种基于学习的高维数据c-近似最近邻查询算法[J].软件学报，2012，23（8）：2018-2031.

[9] 李松，张丽平，刘艳，等. 障碍物环境下的动态单纯型连续近邻链查询[J].计算机工程，2014，40（8）：52-57.

[10]张丽平，李松，郝忠孝，等. 障碍物增减情况下的单纯型连续近邻链查询[J].计算机工程与应用，2015，51（11）：99-113.

[11]GAO Yunjun， ZHENG Baihua. Continuous Obstructed Nearest Neighbor Queries in Spatial Databases[C]. Proceedings of the 28th ACM SIGMOD International Conference of Management of Data，2009，9（4）： 577-590.

[12]MOKBEL MF， CHOW CY， AREF WG.The Newcasper： Query Processing for Location Services Without Compromisingprivacy[C]// International Conference on Very Large Data Bases， 2009， 34（4）：763-774.

[13]HUANG Yuan-Ko， CHEN Chao-Chun， LEE Chiang. Continuous K-nearest Neighbor Query for Moving Objects with Uncertain Velocity[J]. Geoinformatica，2009，13（1）： 1-25.

[14]孫冬璞，郝晓红，高爽，等. 概率可视最近邻查询算法[J].哈尔滨理工大学学报，2013，18（6）：58-63.

[15]郝忠孝. 时空数据库查询与推理[M].北京：科学出版社，2010.

[16]JUJR SACK.Handbook of Computat-ional Geometry[M]. Ottawa： Elsevier Science，2000：829-876.

[17]ZHANG J， PAPADIAS D， MOURATIDIS K， et al.Spatial Queries in the Presence of Obstacles[R]. Lecture Notes in Computer Science， 2004， 2992：366-384.

[18]BERG M De， KREVELD M Van， OVERMARS M， et al. Computational Geometry： Algorithms and Applications[C]. Library Philosophy & Practice，2011（1）：333-334.

[19]XIA C， HSU D， TUNG AKH. A Fast Filter for Obstructed Nearest Neighbor Queries[J]. Key Technologies for Data Management，2004，3112：203-215.

[20]SHARIR M， SCHORR A.On Shortest Paths Inpolyhedral Spaces[J]. SIAM Journal on Computing， 1987，15（1）：193-215.

[21]GHOSH SK， MOUNT DM.An Output Sensitive Algorithm for Computing Visibility Graphs[J]. Foundations of Computer Science Annual Symposium on，2012，20（5）：11-19.

[22]LI Chuanwen， GU Yu， LI Fangfang， et al. Moving K-nearest Neighbour Query Over Obstructed Regions[C]// Advances inWeb Technologies Application， 2010：29-35.化研究[J].信息技术，2008，32（1）：78-79.