牵引供电系统建模及其对电网谐波的影响

郭彭昱，赵闻蕾

(大连交通大学 电气信息学院，辽宁 大连 116028)

0 引言

近年来，我国电气化铁路的快速发展在为国民带来便利的同时也为电力系统带来了谐波等影响电能质量的问题.随着人们对电能质量的要求越来越高，由电气化铁路引起的电能质量问题也越来越受到重视[1].

针对牵引供电系统引起的谐波问题，国内外学者对此进行了大量研究.文献[2- 3]建立了牵引网数学模型，利用计算机编程进行计算；文献[4- 5]研究了牵引网阻抗参数计算；文献[6- 7]建立了记及牵引网的牵引供电系统仿真模型，但都只考虑了牵引网阻抗的影响；文献[8- 9]建立了牵引网与牵引负荷的联合仿真模型，但牵引负荷采用恒功率源模型或只仿真分析了交-直车型.上述文献在研究牵引供电系统引起的谐波问题时，忽略了牵引网的建模，或者只考虑了牵引网线路阻抗的影响，而没有考虑导纳的影响，牵引供电系统模型不够准确.对于牵引负荷模型，上述文献往往采用恒功率源的简化模型，不能准确反映谐波源对电网的影响.

本文利用Matlab/Simulink仿真软件，对AT牵引供电系统、交-直型电力机车SS9、交-直-交型电力机车CRH2进行详细建模，将车、网模型联合在一起，仿真研究牵引负荷在不同位置、数量以及车型混跑时牵引供电系统对电网谐波的影响.

1 牵引供电系统

牵引供电系统的组成如图1所示.对于外部电源、牵引变压器以及自耦变压器的模型采用文献[6]的方法进行搭建，其中对于自耦变压器，本文每15 km设置一台.

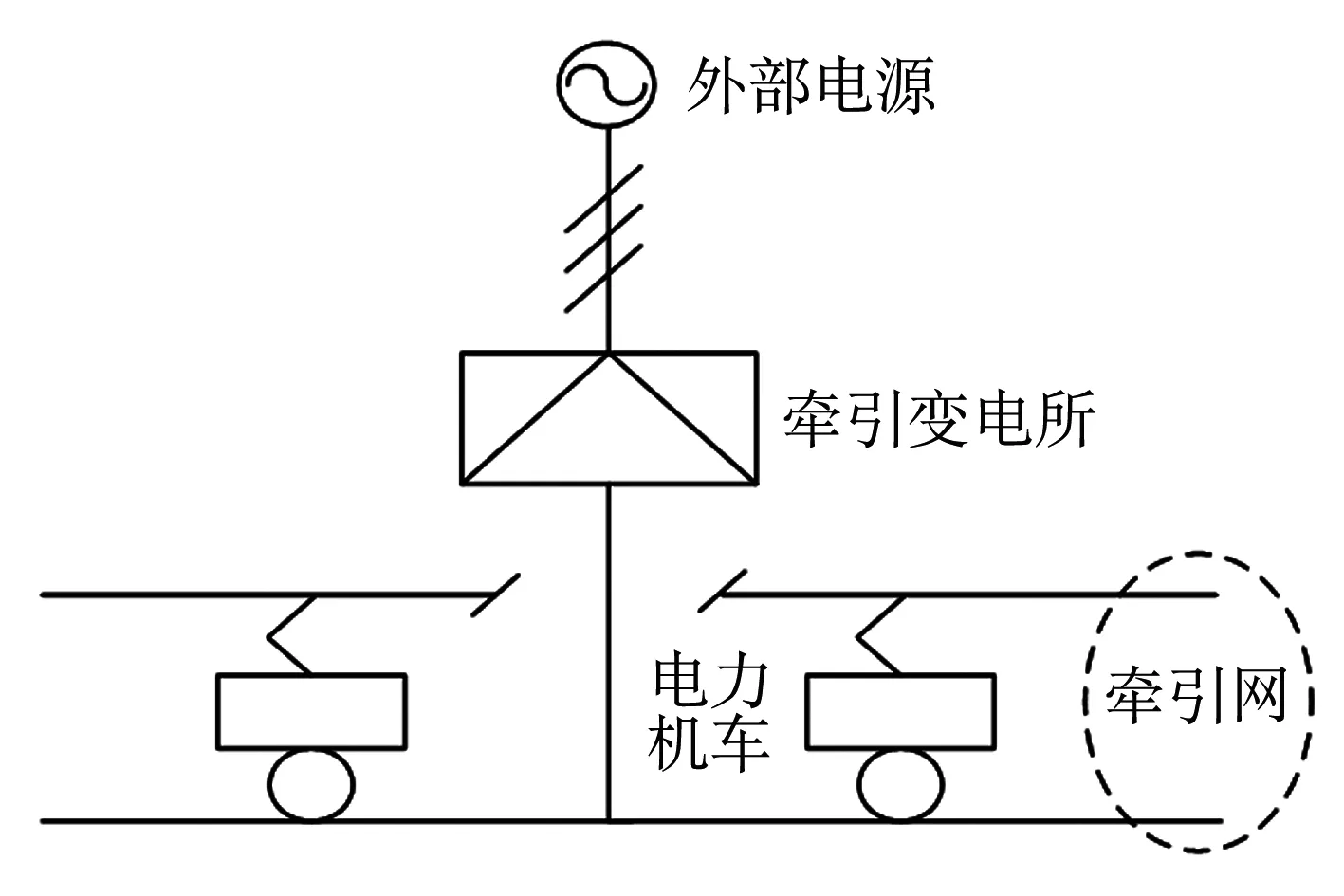
图1 牵引供电系统结构图

1.1 AT牵引网模型

AT牵引网由接触悬挂、钢轨、馈线、保护线、横向连接线、辅助连接和(双线)横向连接构成[3].根据这些导体在电气特性上的连续和相关性，通过应用电力系统的多导体传输线(Multi-conductor Transmission Line,MTL)理论，结合铁路牵引网线路较短、分布连续的特点[6,10]，最终将牵引网等效为相互平行的8根导体，分别是上(下)行接触线T1(T2)、钢轨R1(R2)、负馈线F1(F2)和保护线PW1(PW2).

因本文主要研究牵引供电系统对电网总谐波畸变率的影响，不考虑牵引网谐波的传输特性，因此对于牵引网的模型，采用单位长度的等值π型集中参数模型来模拟牵引网每条供电臂的方法.该模型包含单位长度牵引网的串联阻抗矩阵和并联导纳矩阵[11]，其中串联阻抗矩阵包含导线的自阻抗以及导线间的互阻抗；而对于并联导纳矩阵，由于每个供电区段相对比较短，电导G影响作用较小，通常忽略电导[12]，因此并联导纳矩阵包含导线对地电容及其导线间的电容.

对于钢轨导线，为了更加符合实际情况，考虑了其对地漏导，即在仿真模型中钢轨导线两端各加一个对地电阻，使模型更加精确[13].通过该单位长度等效模型可以扩展为任意长度线路模型.

1.1.1 串联阻抗矩阵

基于Carson理论和MTL理论，AT牵引网可以简化等效为由几个“导线-地回路”和“钢轨-地回路”等所构成的电路，计算各回路的自阻抗和两回路的互阻抗，即可求出牵引网阻抗.

在工频下，任意导线地回路的单位自阻抗

(1)

两回路的单位互阻抗

(2)

在式(1)、式(2)中，Z1为回路1的单位自阻抗，Ω/km；Z12为回路1、2的单位互阻抗，Ω/km；r1为回路1的导线有效电阻，Ω/km；Req1为回路1的导线等效半径，mm；d12为回路1、2的导线的中心距离，mm；Dg为等效地回线的入地深度，cm.

其中，等效地回线的入地深度

(3)

式中，f为电流频率，Hz；σ为大地电导率，1/Ω·cm.

本文采用单链形悬挂牵引网系统，利用文献[3]的方法，将单链形悬挂系统等效为“接触网-地回路”和“钢轨-地回路”，其中，“接触网-地回路”由“接触线-地回路”和“承力索-地回路”并联而成.之后分别计算各回路的自阻抗及两回路间的互阻抗，求出牵引网串联阻抗矩阵.

1.1.2 并联导纳矩阵

导纳矩阵的计算即电容矩阵的计算.导线电容的计算是基于电磁场理论和镜像法进行的[14].设n条平行架设且与地面平行的导线和大地构成一个多导线系统，每一导线i的对地电位ui与该导线上的线电荷密度qi的关系如下：

(4)

式中,P为电位系数矩阵，(F/m)-1；ui为导线i的对地电位，V；qi为导线i的线电荷密度，C/m.

将方程(4)左右同乘P-1，可以得到

Q=P-1U=BU

(6)

式中，B矩阵为电容系数矩阵，又称为静电感应系数.

因此可得

(7)

导线i的对地电容Cig、导线i、j之间的部分电容Cij与静电感应系数B的关系为

Cig=bi1+bi2+…+bin,i=1，2，…,n

(8)

Cij=-bij,i,j=1，2，…,n

(9)

因此可得电容矩阵C，F/km.

通过镜像法可求得电位系数矩阵P，如图2所示.

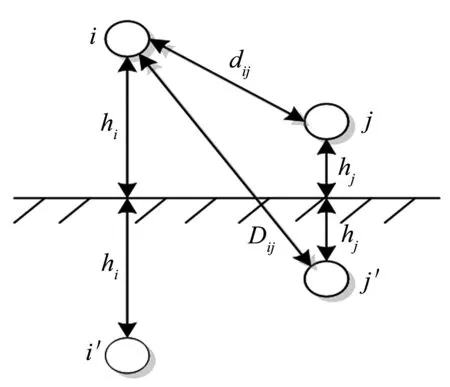
图2 导线镜像

可得电位系数矩阵P

(10)

式中，Pii为导线i的自电位系数；Pij为导线i、j之间的互电位系数；ε0为真空介电常数，ε0=8.854 2×10-9F/km；hi为导线i到达地面的高度，mm；dij为导线i、j之间的距离，mm；Dij为导线i和镜像导线j′之间的距离，mm.

最后，采用文献[13]的方法，对并联导纳矩阵进行降阶等值处理，最后合并简化为复线AT牵引网的8导线等值模型.

1.2 电力机车模型

1.2.1 韶山9型电力机车模型与谐波特性

SS9型电力机车采用三段不等分半控整流桥和晶闸管磁场分路电路.其速度特性v=f(Id)如式(11)所示[15].

(11)

式中，v为电力机车速度，km/h；D为车轮直径，m；Ud为牵引电机端电压，V；Id为牵引电机电枢电流，A；Rd为牵引电机回路电阻，Ω；μc为齿轮传动比；φ为牵引电机磁通量，Wb；Ce为牵引电机常数.

司机通过调节手柄级位来控制运行中的电力机车的电枢电流和速度大小，控制函数如式(12)所示[15].

(12)

式中,Id为牵引电机电枢电流，A；k为控制手柄级位；v为机车速度，km/h.牵引电机设定电流Id为三个值中的最小值.

每一段整流电路晶闸管的触发角θ由下式求得

(13)

之后根据电力机车速度特性公式以及设置电力机车的速度和运行级位，计算出牵引电机所需的整流电压Ud之后就可以求得整流电路晶闸管触发角θ以此产生触发脉冲.

当SS9型电力机车运行在第二段且速度为80.5 km/h时，机车取流的FFT分析频谱如图3所示.通过与文献[16]的研究结果对比，验证了本文所搭SS9型电力机车模型的正确性.

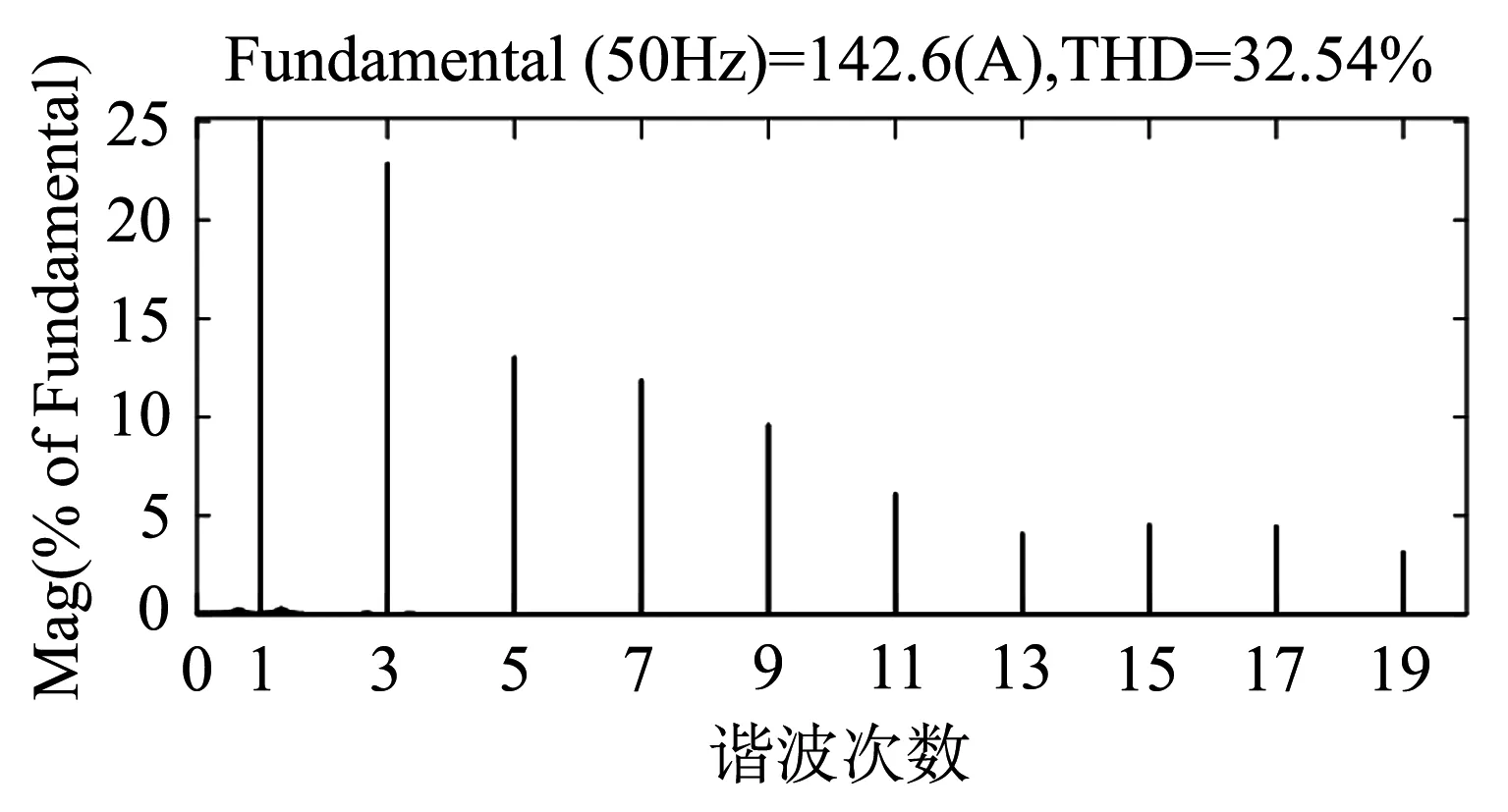
图3 SS9型机车取流FFT谐波分析

1.2.2 CRH2型电力机车模型与谐波特性

我国生产的CRH2型电力机车广泛采用三电平脉冲整流器.由于列车的直流环节将整流器与逆变器进行了隔离[17]，因此用三电平脉冲整流器带负载来模拟CRH2电力机车模型，仿真模型主要包括电源、车载变压器、单相三电平脉冲整流器及其控制系统、中间直流环节、负载电阻等.中间直流输出电压为3 000 V，载波比25.

三电平脉冲整流器采用SPWM调制方式，控制采用电压外环电流内环的双闭环控制，脉冲整流器电流控制策略采用瞬态直接电流控制[18]，其数学公式为

(14)

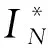
当CRH2型机车运行在牵引工况时的机车取流FFT分析频谱如图4所示.通过与文献[19]的理论分析进行对比，验证了CRH2模型的正确性.

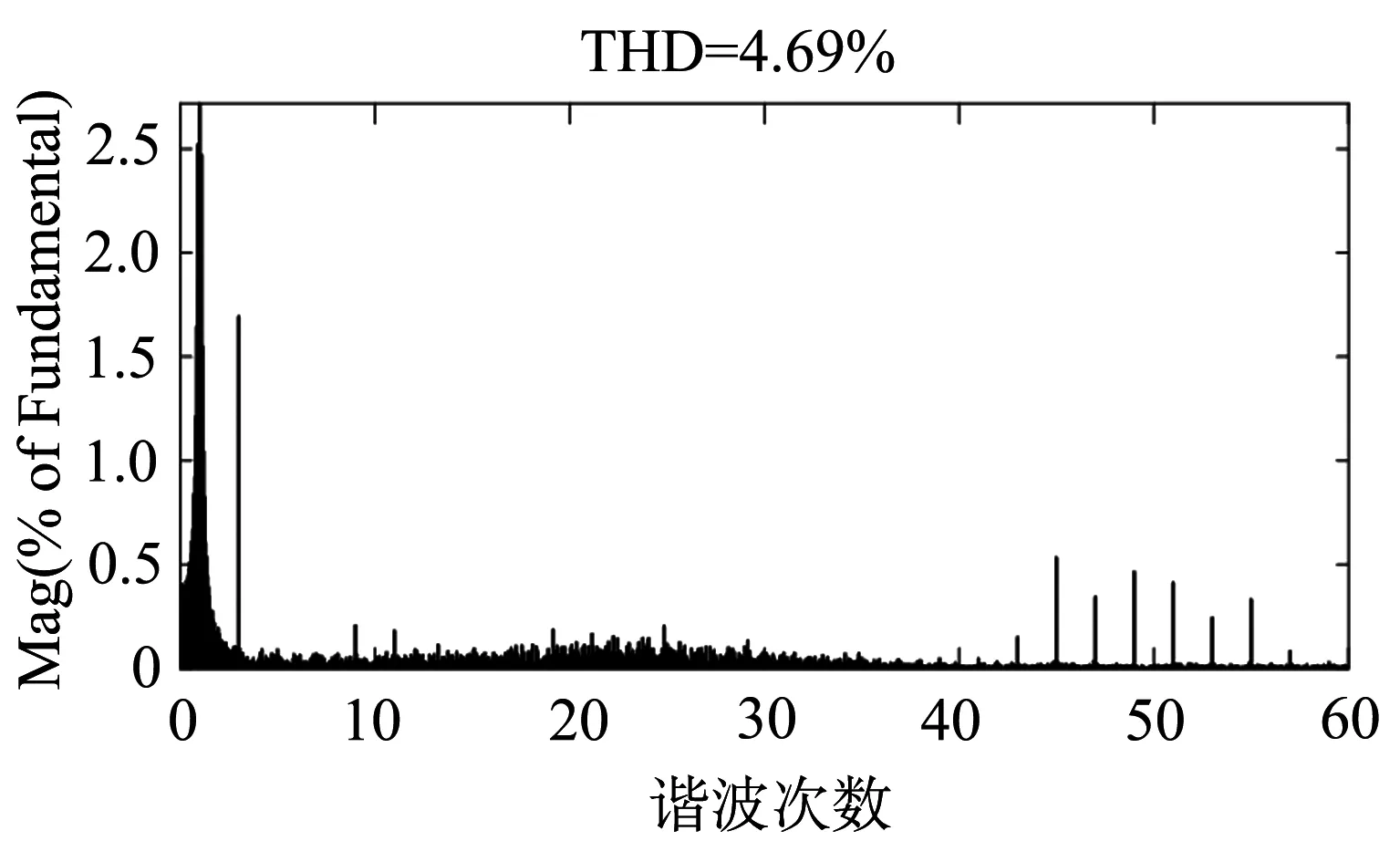
图4 CRH2型机车取流FFT谐波分析

2 系统仿真分析

2.1 仿真条件及其参数设置

本文以Vx接线型牵引变压器为例，搭建了AT牵引供电的车-网联合仿真模型，相关的系统仿真参数如表1所示.

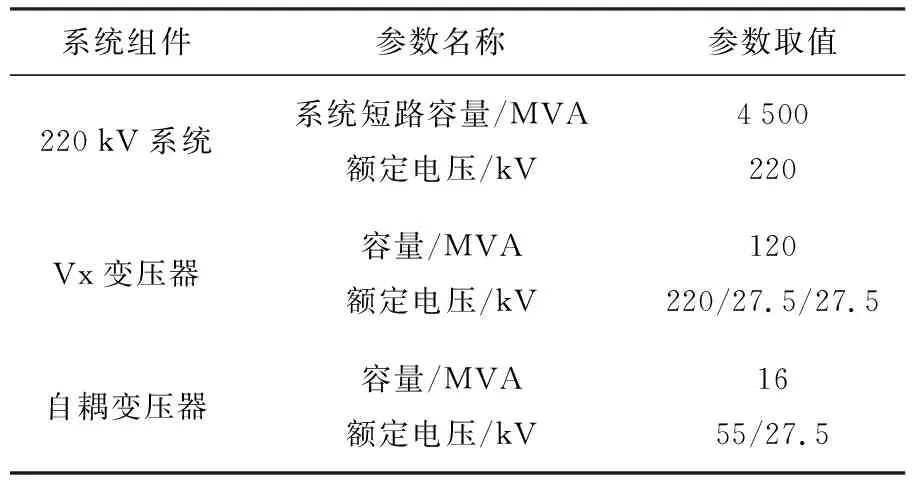
表1 系统参数取值

牵引网线路的计算以某牵引变电所为例，其牵引网悬挂系统空间分布如图5所示.牵引网导线数据均为施工常用典型数据[12].

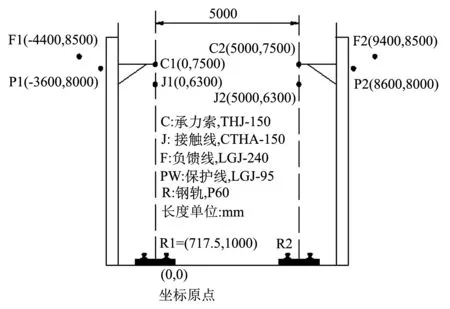
图5 AT牵引网纵向截面结构图

为了更加符合实际，取钢轨导线对地漏导为0.2 S/km[13].将15个单位牵引网模块级联成一个牵引网子模块，之后再由三个牵引网子模块组成单臂长45 km的复线牵引网.

2.2 牵引网稳态电压仿真分析

为了对比分析牵引网电压在不同负荷数量下的分布情况和机车端电压在不同位置下的波动特性，设置机车在不同位置和不同数量下仿真算例进行分析，仿真结果如图6、图7所示.

由图6、7可知，负荷数量越多，牵引网电压普遍越低.机车端电压的总体变化趋势是随着机车远离变电所而降低，尽管由于自耦变压器的作用，在自耦变压器处有一定升高.机车端电压的实际值较额定电压波动4%，满足系统对电压4.5%的波动要求[12].仿真结果与文献[8、12]中的结论吻合，验证了模型的正确性.

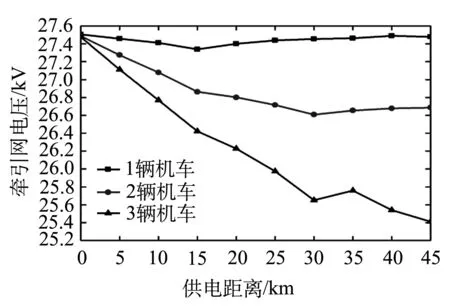
图6 机车不同数量下牵引网电压

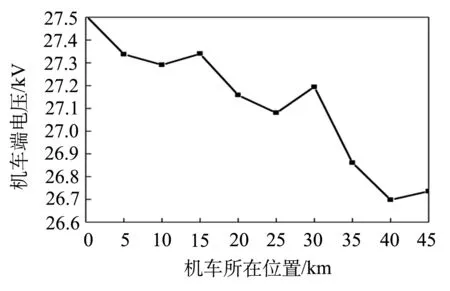
图7 机车端电压分布曲线

2.3 牵引供电系统引起的谐波畸变仿真分析

(1)牵引负荷位置变化对电网谐波畸变的影响

设定牵引负荷分别位于距离变电所0、15、30、45 km处时，电网侧、变电所以及机车取流的总谐波畸变率变化曲线如图8所示.

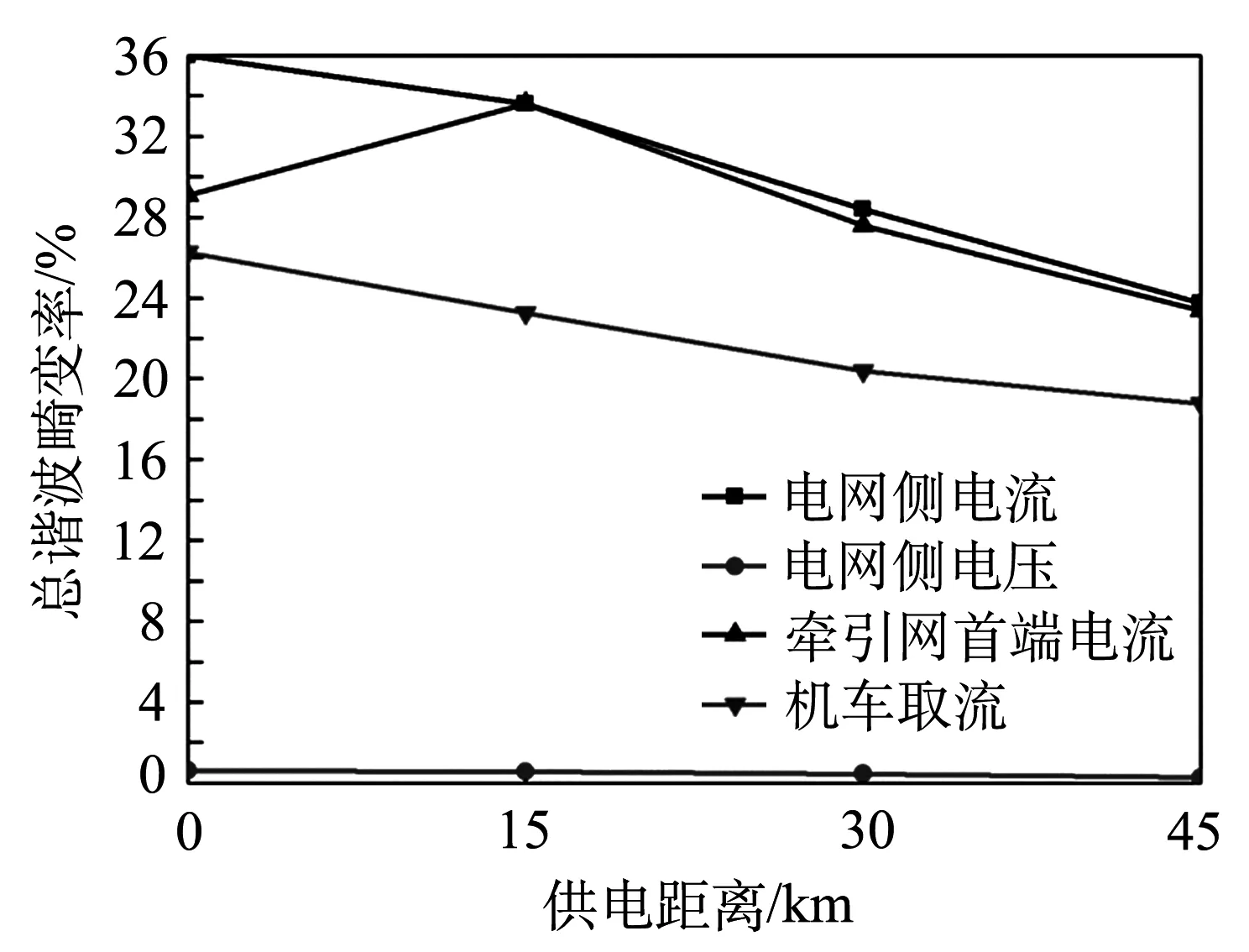
图8 机车位置变化下的总谐波畸变率

由图8可以看出，机车驶离变电所时，电网侧、变电所和机车取流的电流总畸变率以及电网侧的电压总畸变率逐渐下降.

(2)牵引负荷数量变化对电网谐波畸变的影响

设定在距离牵引变电所15、30、45 km处，上、下行各1辆车、2辆车、3辆车自近及远依次增加和自远及近依次增加共五种仿真情况，得到电网侧和变电所总谐波畸变的仿真结果如表2所示.

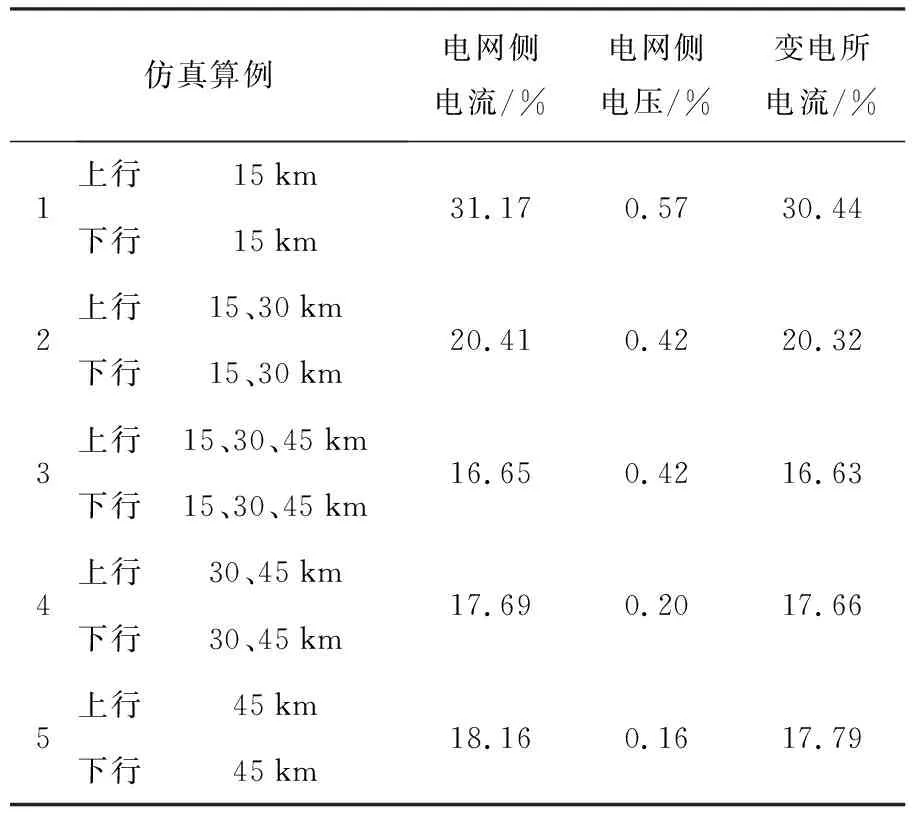
表2 机车数量变化时谐波畸变率

由表2可知，这种仿真算例必然带来位置的变化.同样是机车数量的增加，距离牵引变电所由近及远变化和由远及近变化的仿真结果变化幅度不一样，尤其是电网侧电压的畸变率，呈现出了完全相反的变化趋势.由此可以看出，牵引负荷运行位置与牵引变电所的距离仍然是影响牵引供电系统谐波畸变率的主要因素.

为了更加准确验证机车数量对牵引供电系统谐波畸变的影响，再次设定了同一位置下，上行1辆车与上下行各一辆车的仿真算例，仿真结果如表3所示.

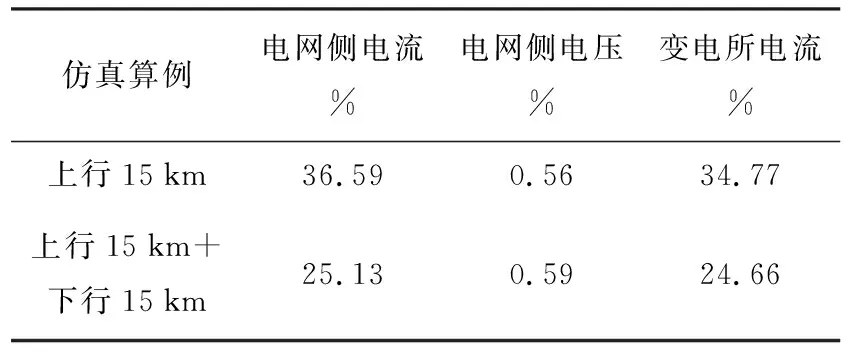
表3 固定位置下机车数量变化时谐波畸变率

由表3可知，在同一位置下，增加牵引负荷运行数量使电网侧电流、牵引变电所电流总谐波畸变率下降，电网侧电压总谐波畸变率上升.

(3)牵引负荷车型变化对电网谐波畸变的影响

设定在牵引变电所30 km处，上行SS9型、下行CRH2型电力机车在牵引工况下同时行驶时的谐波畸变情况，得到电网侧电流的FFT谐波分析仿真结果9所示.

由图9可以看出，交-直和交-直-交车型的牵引负荷混跑运行时引起的电网电流不仅包含了交-直机车产生的低次谐波，也包含了交-直-交机车产生的高次谐波，谐波频谱变宽，但低次谐波仍是主要成分，电流总畸变率较仅有交-直机车运行时降低很多.

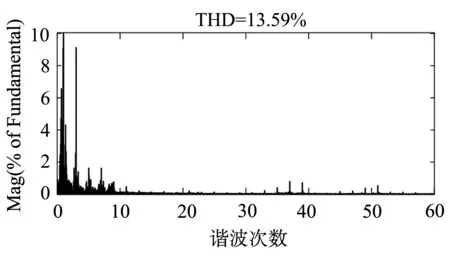
图9 SS9型与CRH2型混跑时的 电网侧电流FFT谐波分析

3 结论

本文基于Matlab/Simulink仿真软件，建立了车-网联合仿真模型，对牵引负荷在不同运行位置、数量、型号时牵引供电系统对电网谐波的影响进行了仿真分析，得出如下结论：

(1)考虑牵引网阻抗导纳影响的牵引供电系统车-网联合模型能更准确地反映出牵引供电系统对电网谐波的影响情况，为后续谐波治理等研究打下一定的基础；

(2)牵引供电系统的运行对电网谐波畸变的影响很大.当牵引负荷运行在牵引变电所附近时、当牵引负荷运行数量过少时、当只有交-直车型的牵引负荷运行时，均会使电网侧电流的总谐波畸变增加.交-直机车与交-直-交机车混跑时，还会引起电网电流谐波频谱变宽的问题.对于电网侧电压总谐波畸变率，会在机车牵引负荷驶离变电所时降低，牵引负荷运行数量增加时上升.