城市轨道交通第三轨受流器动态特性试验及分析
2018-07-24骆海坤
王 鹏 骆海坤
(1.华中科技大学船舶与海洋工程学院,430074,武汉;2.中交机电工程局有限公司武汉技术中心,430050,武汉//第一作者,硕士)
城市轨道交通的受电方式主要有架空接触网受电与第三轨受电两种方式。第三轨受电相比接触网受电具有结构简单、美观、电能损耗小等优点,因此第三轨受电方式被越来越多城市的轨道交通线路所采用。
本文在分析中外文献关于第三轨受流系统研究结果的基础上,以无锡地铁2号线第三轨受流系统为试验对象,对靴轨关系进行试验研究,为后续相关第三轨受流系统的设计研究提供参考。首先,对受电靴靴头施加静载荷,建立靴头所受载荷与摇臂根部应变关系,并进行静态标定。其次,通过靴头的垂向振动加速度与摇臂根部的应变反推出受电靴与接触轨之间的接触压力,研究不同速度下接触压力的分布情况、受电靴的振动情况。通过位移传感器与加速度传感器,研究受电靴以不同的速度通过端部弯头的动态特性。
1 试验系统
整套测试系统包括加速度传感器、位移传感器、应变片和数据采集仪。整体安装示意图如图1~2所示。
在受流器靴头底面布置3个方向互相垂直的加速度传感器和1个冲击型加速度传感器。冲击型加速度传感器用以测量受电靴在较高速度下与轨道不平顺处(如膨胀接头、端部弯头等)所产生的垂向加速度。因滑靴上带有750 V高压电,所以在滑靴底部与加速度传感器之间需安装绝缘的环氧树脂型基座。
在摇臂的根部左右两边对称安装了1组全桥应变片。摇臂根部上下表面对称布置1个十字型90度应变花,上下2个应变花组成的全桥接入应变试调器连接到数据采集仪。两组应变平均值即为静态接触压力在摇臂中所产生的变形大小。
位移传感器安装在受流器电气箱的顶部。并在摇臂上安装一支座用来连接位移传感器的两端。位移传感器直接测量得到摇臂上一点到受流器顶部的距离。通过几何关系换算得到滑靴的垂向位移。

图1 试验仪器安装示意图

图2 靴头底部加速度传感器安装示意图
应变试调器采用DH3818动态应变试调器,它输出的信号用1 kHz的频率进行采样。当列车运行速度为80 km/h时,采样间距为22.22 mm,远小于三轨支座间距,因而能够准确检测由于三轨支座安装不良而造成的轨靴间接触压力的异常变化。
2 试验原理
理想情况下,应当采用直接测量法测量靴轨之间的接触压力,但因传感器使用环境以及高压电的缘故,本文采用间接法测量。受电靴受力简化模型如图3所示。

注:FS为靴轨之间的静态接触压力,FC为滑靴在垂向方向上受到的接触压力,a为加速度
图3 受电靴受力简化模型示意图
滑靴简化模型所受接触力为:
FC=FS+ma
(1)
式中:
m——滑靴质量。
FS通过摇臂根部的应变桥路测量得到;a通过滑靴底部垂向加速度传感器测量得到;m通过测量滑靴几何几寸,并根据所用材料密度换算得到。
通过对受流器进行静态标定试验可得到FS与摇臂根部应变ε的换算关系式FS=K×με(με为微应变)。在滑靴底部挂上不同大小的质量块,测试得到相应加载质量的应变读数,对应变数据与静态加载力进行线性拟合得到系数K。
3 试验结果与分析
3.1 静态标定试验
通过在受电靴靴头下部,加载不同质量块,测量得到受电靴根部应变与滑靴受力之间的对应关系。静态试验如图4所示。

图4 静态标定试验示意图
重复进行3次静态标定试验,对于每一个静态加载质量,取3次试验数值的平均值作为该静态加载质量下的应变值。摇臂根部应变与静态加载质量的线性拟合如图5所示。

图5 摇臂根部平均微应变与静态加载力的线性拟合图
由图5可得出静态加载力与平均微应变的关系:FS=0.222 4 με。两者的相关系数R2为0.999 7,表明靴头底部所受的静载荷与摇臂根部的应变具有良好的线性关系。通过此关系式可根据应变值推导得到靴头所受的FS。
3.2 接触压力分析
无锡地铁2号线的受电靴与接触轨之间的接触压力设定范围为125 N±20 N。图6~9为不同速度下,静态接触压力、靴头垂向振动加速度、靴头抬升高度的试验曲线。按照试验原理中所阐述的模型,对试验得到的数据进行分析处理。静态接触压力由布置在受流器摇臂根部的应变组件测量得到,动态接触压力由靴头垂向振动加速度与靴头质量的乘积构成。静态接触压力与动态接触压力之和即为受电靴与接触轨之间的接触压力。试验时,选取线路上纺织城站与渣桥站作为试验区间,该试验区间的线路较为平坦,线路长。试验时,测量每一种速度下列车往返4次的数据,对数据进行平均处理以减小试验误差。

a) 接触压力

b) 垂向振动加速度
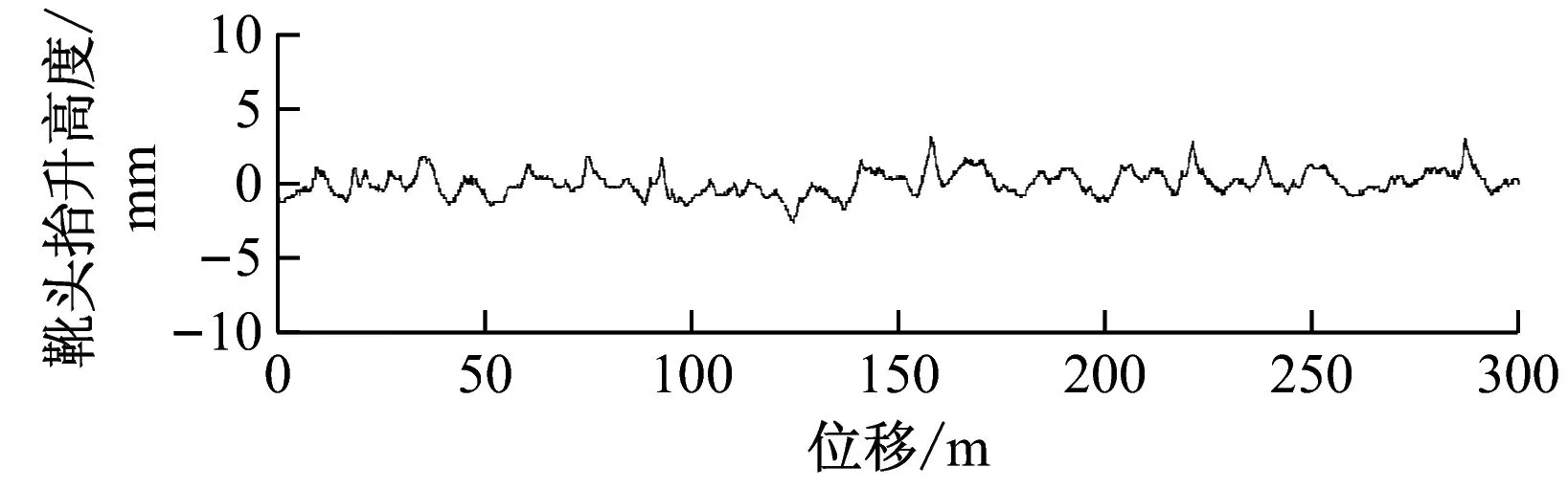
c) 靴头抬升高度

a) 接触压力

b) 垂向振动加速度

c) 靴头抬升高度

a) 接触压力
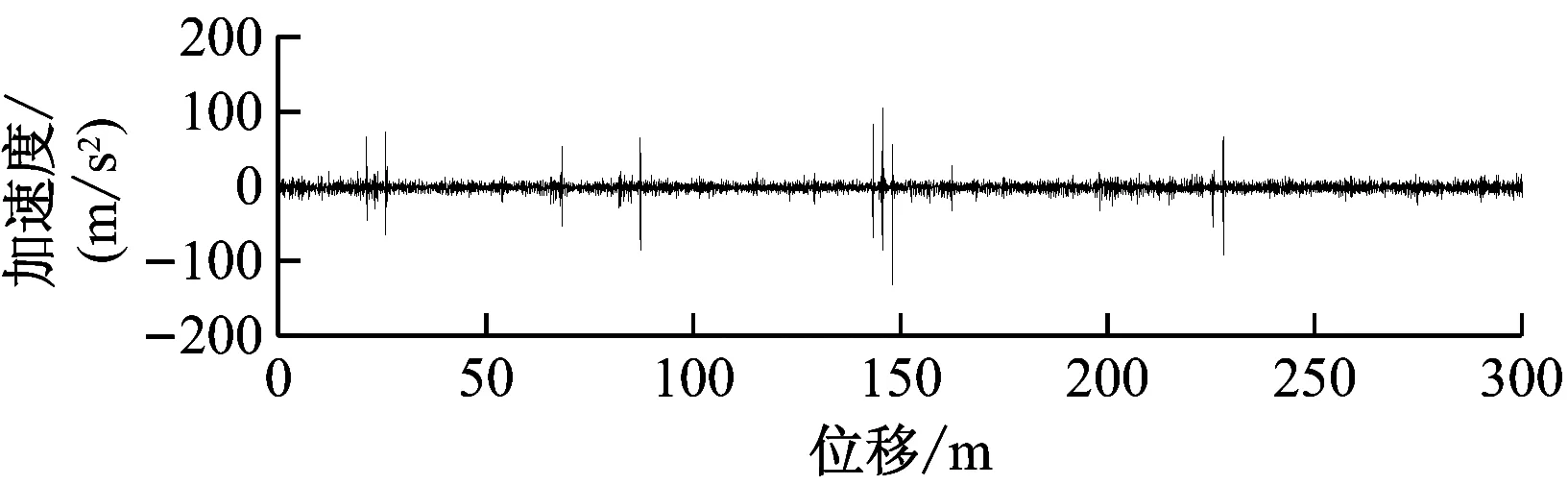
b) 垂向振动加速度

c) 靴头抬升高度

a) 接触压力
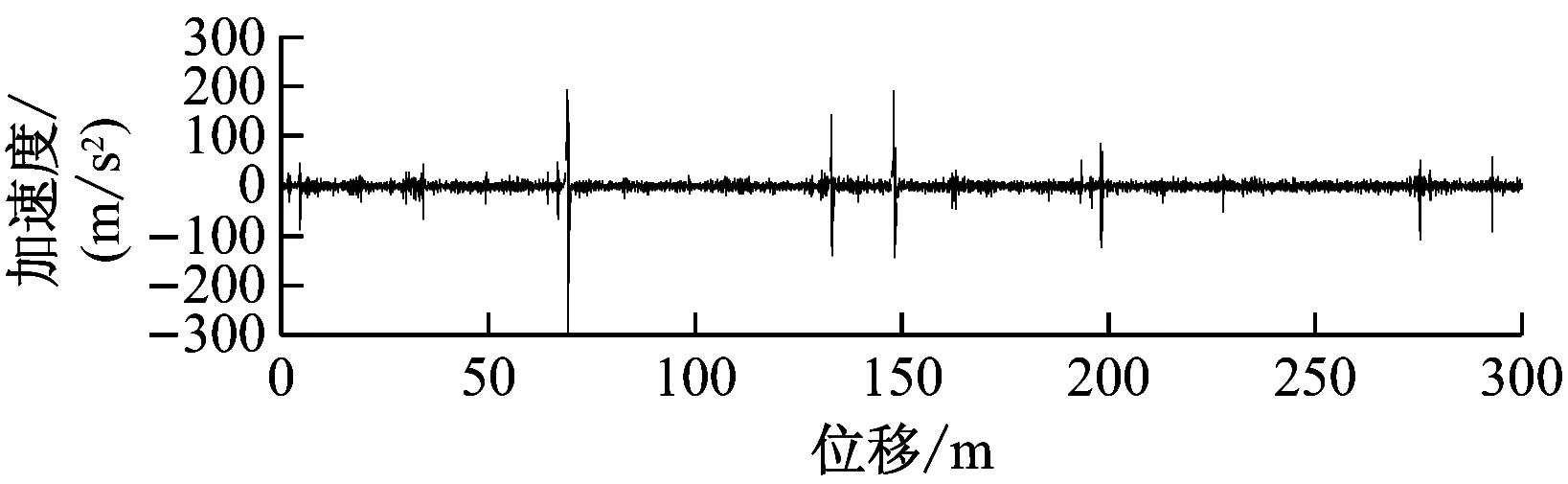
b) 垂向振动加速度
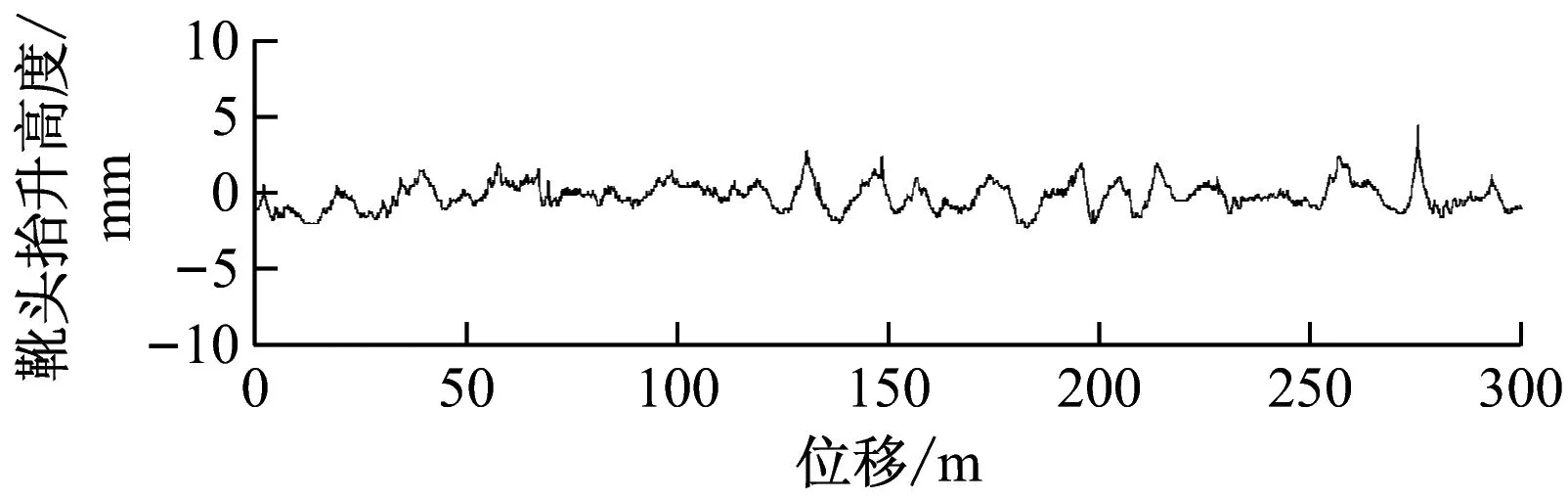
c) 靴头抬升高度
对接触压力数据进行概率统计分析,不同速度下接触压力的概率分布如图10所示。从图10中可以看出,20 km/h与40 km/h速度下的接触压力分布规律相近,60 km/h与80 km/h速度下的接触压力分布规律相近;20 km/h与40 km/h曲线较60 km/h与80 km/h的概率密度曲线高、瘦,说明其波动较小。

图10 不同速度下接触压力概率分布图
参考刚性接触网-受电弓系统受流质量评价指标[6],轨靴间接触压力分析引入标准差S。
(2)
式中:
n——采样数目;
Fm——接触压力平均值;
Fi——第i个采样接触压力。
采用S与Fm的比值来衡量受电靴的动态性能,当S/Fm<20%时则认为靴轨间动态性能良好。表1为接触压力试验结果统计表。
从表1可以看出,4种列车运行速度下的S/Fm都小于20%,说明不同速度下的靴轨动态性能都较为良好;随着列车运行速度的增大,接触压力标准差越大,波动越大。

表1 不同速度下接触压力试验结果统计表
3.3 受电靴振动特性分析
通过布置在受流器电气箱顶部的拉线式位移传感器,测量得到摇臂上固定点与拉线式位移传感器固定点之间的距离。根据几何关系,将拉线式位移传感器所测得数据换算为列车运行过程中受电靴靴头抬升量的变化。通过布置在靴头底面的加速度传感器,试验测量得到受电靴的垂向振动加速度。参考刚性接触网-受电弓系统受流质量评价指标[7],受电靴受流过程振动分析引入受电靴最大垂直振幅A。A越小,表明受电靴的运动轨迹越平滑,受流质量越好。
(3)
式中:
Hmax——跨距内受电靴最大高度;
Hmin——跨距内受电靴最小高度。
表1为不同速度下的试验数据统计。从表1中可以看出,垂向振动加速度随着列车运行速度的增大,其振动的峰值与波动也越大,说明靴头的振动也越剧烈;列车在4种运行速度下,靴头的最大垂直振幅都在5 mm以下;随着列车运行速度的提高,靴头动态高度变化的幅值与标准差逐渐增大,但各速度下的标准差的差距很小,表明受电靴与接触轨的跟随性较好。

表1 不同速度下试验数据统计表
3.4 受电靴与接触轨端部弯头接触特性分析
接触轨布置的一般原则为尽量减少断轨,保证接触轨的连续性要求,但在一些特殊区段如车站检修扶梯处、人防门/防淹门处、区间疏散平台扶梯处等,需要设置断口。接触轨断口的存在,不可避免地会对列车的连续可靠受流产生一定影响。
本文试验选取某车站站点一端的接触轨弯头作为试验对象,试验研究了受电靴在20 km/h、30 km/h、40 km/h 3种列车运行速度下,与低速弯头的接触特性。图11为受电靴在不同速度下,通过弯头时的运动轨迹以及靴头的垂向振动加速度。
从图11可以看出,随着列车运行速度的增加,受电靴滑离弯头时的波动加剧,受电靴撞击弯头时靴头高度的变化量也加大。但从靴头高度变化量可以看出,靴头在40 km/h的速度下撞击弯头并没有脱离接触轨,与接触轨之间接触良好。
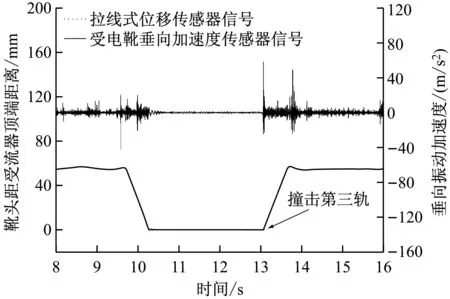
a) 速度为20 km/h
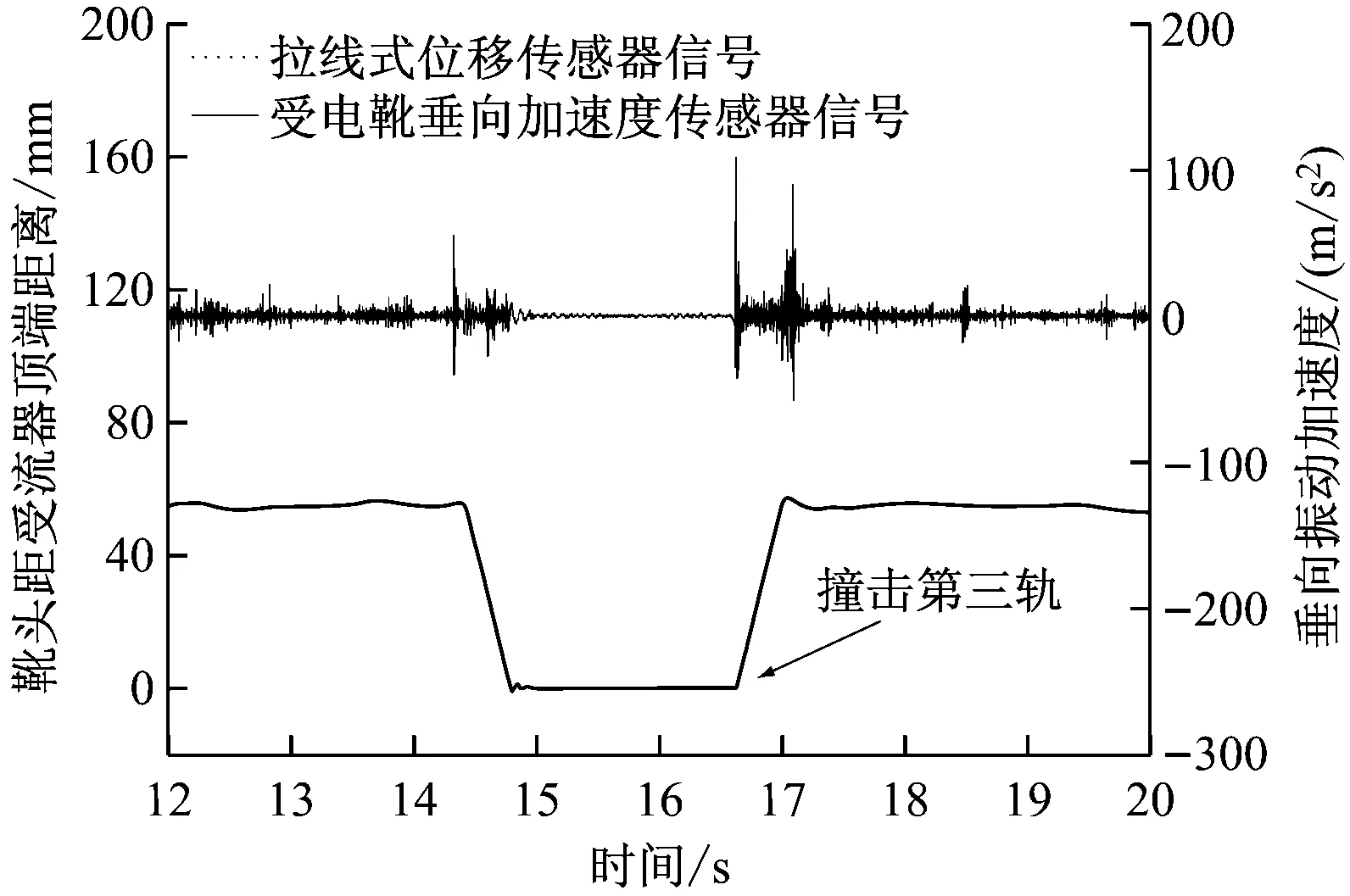
b) 速度为30 km/h

c) 速度为40 km/h
表2为受电靴以不同速度通过端部弯头时,靴头垂向振动加速度的峰值。从表2可以看出,受电靴随着撞击速度的增加,撞击产生的加速度峰值也越大。

表2 受电靴不同速度通过时靴头垂向振动加速度峰值比较表
以列车起动位置为0位置,图12为受电靴以不同速度通过端部弯头的运动轨迹对比图。由图12可见,随着列车运行速度的增加,受电靴脱离端部弯头后的波动也越大,但都在几秒内趋于平稳。受电靴以40 km/h速度脱离端部弯头时振幅最大,约为1.5 mm。

a) 受电靴与端部弯头接触运动轨迹

b) 图9 a)中A部放大图
4 结论
本文通过无锡地铁2号线受电靴与接触轨试验,探讨了不同速度下,受电靴与接触轨之间的接触压力、垂向振动加速度、靴头抬升量等物理量的变化,并研究了低速下受电靴与端部弯头之间的接触特性。试验分析得到如下主要结论:
(1)靴头所受的静载荷与摇臂根部的应变具有很好的线性关系,可以用来推导得到靴头所受的静态接触压力。
(2)在接触轨连续段内,20 km/h到80 km/h速度范围内,列车运行速度对平均接触压力的影响不显著;随着列车运行速度的增加,接触压力的波动、受电靴的振动也越剧烈。
(3)在接触轨端部弯头处,受电靴滑上弯头时,随着列车运行速度的增加,冲击加速度也越大,在40 km/h时,冲击加速度大约200 m/s2。
