滚轮轴承最大允许动载荷的计算

刘建志，郭卫东

(常州东风轴承有限公司，江苏 常州 213022)

通过滚轮轴承最大允许动载荷可判断滚轮轴承主参数设计是否合理，若滚轮轴承最大允许动载荷小于滚轮轴承的当量动载荷，则滚轮轴承外圈将会发生弯曲断裂。为设计合理的滚轮轴承主参数，提高滚轮轴承的可靠性，需探讨滚轮轴承最大允许动载荷的计算方法。

1 滚轮轴承主参数的设计

以NUTR类滚子滚轮轴承为例，不带密封圈的满装滚子滚轮轴承主参数为

Dw=KDw(D-d)，

(1)

Dpw=KDpw(D+d)，

(2)

Le=KLeC，

(3)

De=Dpw+Dw，

(4)

D2=De-KD2Dw，

(5)

(6)

(7)

在设计的初始阶段也可取

φ=360°/Z，

(8)

式中：Dw为滚子直径；Dpw为滚子组节圆直径；D为轴承外径；d为轴承内径；KDw为滚子直径系数；KDpw为滚子组节圆直径系数；Le为外圈滚道宽度；KLe为滚道宽度系数；C为外圈宽度；De为外圈滚道直径；D2为外圈挡边直径；KD2为外圈挡边直径系数；Z为滚子数量；δc为相邻两滚子间的周向游隙；φ为相邻两滚子的夹角。

在已知d,D及C的条件下，根据经验可进行主参数的设计，这里不作详细探讨。

2 滚轮轴承外圈截面参数

NUTR类滚子滚轮轴承外圈截面为槽形(图1)，为简化截面参数计算，内边缘直径近似取滚道直径和挡边内径的平均值，外边缘直径取外圈外径，虽对计算精度有影响，但能满足工程应用需要。外圈截面面积为

图1 外圈截面示意图

(9)

外圈中性圆半径为

(10)

外圈形心圆半径为

(11)

外边缘应力系数为

(12)

内边缘应力系数为

(13)

3 滚轮轴承受力分析

3.1 滚子载荷分析

滚轮轴承受载过程中，经历半圈滚子受载到少于半圈滚子受载，但在初始瞬间滚子载荷分布符合Weibull分布，如图2所示。根据文献[1]可知在β=0位置滚子受载最大，最大载荷为

图2 滚子受载示意图

Qmax=4.08Pr/Z，

(14)

式中：Pr为滚轮轴承的当量动载荷。

第i个滚子所受载荷为

Qi=Qmaxcos1.1(iφ)；i=1,2,…,n，

(15)

n=(Z-2)/4。

3.2 外圈受力分析

3.2.1 下半外圈

假想将滚轮轴承的外圈从图2中的x轴线切开后，下半外圈相当于一个中间单支点的简支半圆形梁，其受力状态如图3所示。载荷通过滚子的传递作用在下半外圈上，使下半外圈发生由内向外的法向弯曲变形，而上半外圈有限制下半外圈发生弯曲变形的内力，内力用分界面上的法向拉力和切向剪力表示，上半外圈对下半外圈的法向拉力N垂直于分界面，作用在中性圆上；上半外圈对下半外圈的切向剪力V平行于分界面，同样作用在中性圆上。

图3 下半外圈受力图

由静力学平衡方程组∑Fx=0和∑Fy=0得

(16)

(17)

Frmax=Qmax，

Fri=Qi，

式中：Frmax为β=0位置滚子对外滚道的法向力；Fri为第i个滚子对外滚道的法向力。

由(16)和(17)式得

(18)

(19)

将(15)式代入(18)，(19)式得

N=QmaxKQN，

(20)

V=QmaxKQV，

(21)

3.2.2 上半外圈

上半外圈无外力作用，只存在下半外圈对上半外圈的法向拉力N和切向剪力V,力的方向和作用位置如图4所示。

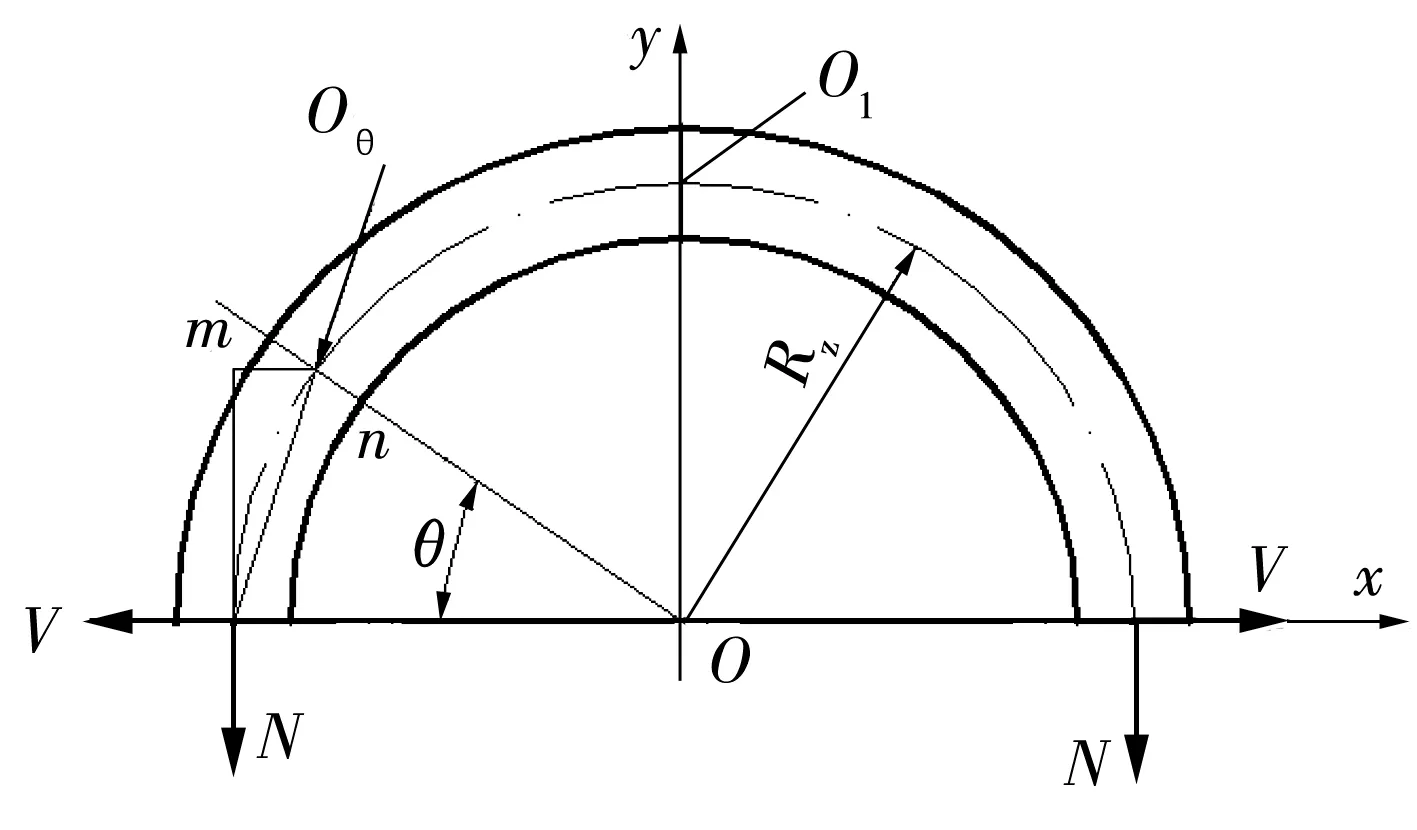
图4 上半外圈受力图

上半外圈任意截面的受力如图5所示，Nθ为任意截面上的法向拉力，Mθ为任意截面上的弯矩。根据力和力矩的平衡关系可得

图5 任意截面受力图

Nθ=Ncosθ+Vsinθ，

(22)

Mθ=Rz[N(1-cosθ)-Vsinθ]。

(23)

4 外圈的边缘应力

根据文献[2]74-77可得上半外圈任意截面外、内边缘应力分别为

(24)

(25)

分别将(22)，(23)式代入(24)，(25)式得

σw={Rz[N(1-cosθ)-Vsinθ]Kw-

(Ncosθ+Vsinθ)}/Ah，

(26)

σn=-{Rz[N(1-cosθ)-Vsinθ]Kn+

(Ncosθ+Vsinθ)}/Ah。

(27)

当θ=0时

(28)

(29)

当θ=90°时，在对称轴线的横截面上有2个弯矩M90，则

(30)

(31)

作用在90°截面上的法向拉力是按V或2V计算还存在不同看法，因V对边缘应力的计算影响较小，故(30)，(31)式中暂取V。

通过(28)～(31)式可知：θ=90°截面上外、内边缘的应力值大于θ=0°截面上外、内边缘的应力值。

为了分析在(0,90°)区间的最大边缘应力与σw90，σn90的关系，对(26)，(27)式求导得

(32)

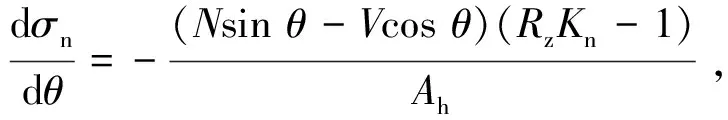
(33)

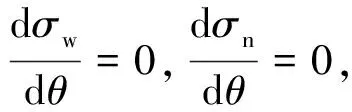
(34)

(35)

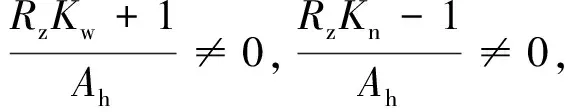
Nsinθ-Vcosθ=0，

(36)

可得

(37)

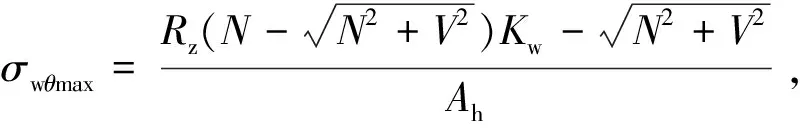
(38)

(39)

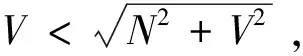
σwθmax<σw90，

(40)

σnθmax<σn90，

(41)

故在[0,90°]区间最大边缘应力发生在θ=90°位置截面上。

下半圈y轴所在截面的弯矩是分界面上的内力对y轴所在截面的弯矩与各法向载荷Fri对y轴所在截面的弯矩差，故作用在下半圈y轴所在截面的弯矩小于上半圈y轴所在截面的弯矩，由此判断最大边缘应力在上半外圈上。

5 最大边缘应力的实例计算

NUTR50和NUTR50110滚轮轴承主参数见表1，分别根据国外某公司样本中的最大允许动载荷Prmax、最大允许静载荷P0rmax、有效额定动载荷Crw、有效额定静载荷C0rw计算最大边缘应力，结果见表2和表3。

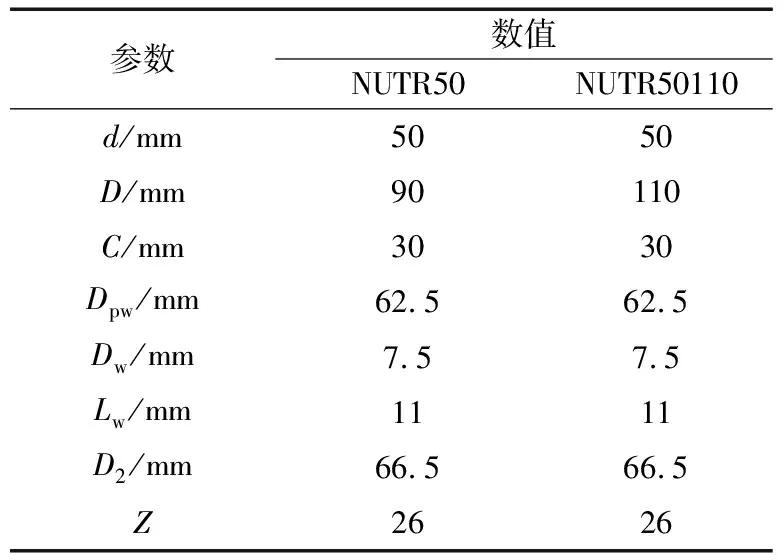
表1 NUTR50和NUTR50110的主参数

由表2、表3可知：当用Crw，C0rw，P0rmax计算外圈的最大边缘应力时，外、内边缘应力无规律性；当用最大允许动载荷计算外圈的最大边缘应力时，NUTR50和NUTR50110外圈的最大外边缘应力σw90很接近，最大内边缘应力σn90也比较接近;用最大允许动载荷计算的最大边缘应力有一定的规律性。由此可推断：滚轮轴承的最大允许动载荷受外圈最大允许边缘应力约束，最大允许动载荷根据最大允许边缘应力计算得到。

表2 NUTR50外圈最大边缘应力

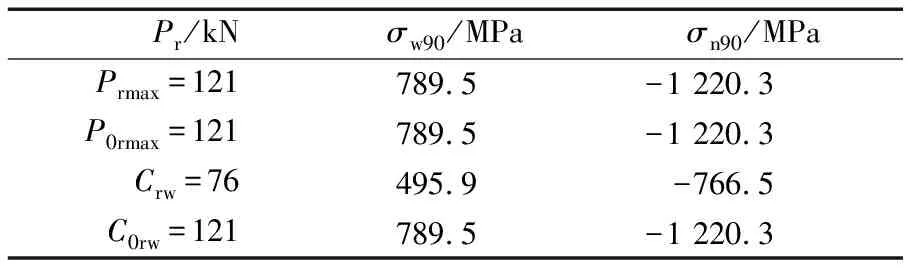
表3 NUTR50110外圈最大边缘应力

6 滚轮轴承最大允许动载荷

将(20)，(21)式代入(30)式得

(42)

由(42)式得到用外边缘应力表示的滚子最大载荷为

(43)

将(22)，(23)式代入(33)式得

(44)

取σn90的绝对值，由(44)式得到用内边缘应力表示的滚子最大载荷为

(45)

由(14)式得

Pr=QmaxZ/4.08，

(46)

将(43)，(45)式分别代入(46)式得到用外、内边缘应力表示的当量动载荷分别为

(47)

(48)

最大边缘应力应满足强度条件，即

(49)

(50)

式中：σtp为材料热处理后的许用抗拉应力；σcp为材料热处理后的许用抗压应力；σb为材料热处理后的抗拉强度；σbc为材料热处理后的抗压强度；Sw为外边缘应力安全系数；Sn为内边缘应力安全系数。

将(49)式代入(47)式得

(51)

将(50)式代入(48)式得

(52)

由于内边缘直径近似取滚道直径和挡边内径的平均值，而外边缘直径取外圈外径，外边缘应力比内边缘应力计算准确度高。若已知许用抗拉强度和许用抗压强度，用(51),(52)式右式的前项计算；若已知材料抗拉强度、抗压强度极限及外、内边缘应力安全系数，则用(51),(52)式右式的后项计算。

边缘应力安全系数可通过以下方法得到：1)根据国外著名轴承公司滚轮轴承样本中的最大允许动载荷及滚轮轴承样品的测量主参数用第3节方法反推；2)根据国外主机制造公司滚轮轴承订货图中的最大允许动载荷和主参数用第3节方法反推；3)根据滚轮轴承应用条件参考文献[2]104-107的推荐值选择；4)通过试验取得。当数据积累到一定程度后就可以形成各类滚轮轴承(包括其他外圆非包容轴承)在不同应用条件下的边缘应力安全系数。

根据文献[3]，对于淬硬的GCr15钢制外圈，σb约2 100 MPa，σbc约3 700 MPa,推算NUTR50和NUTR50110边缘应力安全系数的平均值为Sw=2.67，Sn=3.36。

7 结束语

通过对滚轮轴承外圈的受力分析及强度理论得到滚轮轴承外圈最大边缘应力，并通过实例分析得到：滚轮轴承的最大允许动载荷根据最大允许边缘应力计算得到。通过将最大允许动载荷与当量动载荷对比可验证主参数设计的合理性，并对主参数进行修正。但滚轮轴承的主参数设计不仅与最大允许动载荷有关，还与最大允许静载荷、有效额定动载荷、有效额定静载荷有关，如何计算这些载荷参数及处理主参数设计与各个载荷参数之间的关系，有待后续做进一步的研究。

文中以常见的NUTR50和NUTR50110滚轮轴承滚轮轴承为例分析，其他结构形式的向心滚轮轴承，如深沟球滚轮轴承、角接触球滚轮轴承、圆锥滚子滚轮轴承，也可参照本文的研究方法进行计算。