橡胶辅助热压印成型的数值模拟
2018-07-23傅志红臧公正朱亚威
傅志红,张 磊,臧公正,张 洲,朱亚威
(中南大学机电工程学院 高性能复杂制造国家重点实验室,湖南 长沙 410083)
近年来,随着微米、纳米结构制品在生物医学领域的应用与发展,聚合物材料在光学、化学、生物及微机电领域获得广泛应用[1-2]。目前,聚合物材料的加工成型方法主要为微热压法、微注塑法和激光刻蚀法。相比之下,热压印法由于其低成本、残余应力小、复制率高等优点,已然成为最具潜力的加工成型方法[3-4]。
对于壳状结构制品的制造,传统的方法是通过带有微结构的上模具与下模具进行加工成型,但该方法对配合精度的要求较高,微小偏差便可能造成模具损坏,而且模具配合时极易造成聚合物堵塞。此外,极高的残余应力也会使超薄壁难成型,导致产品质量恶化。针对微压印法的改进,H.Dreuth等[5]提出与微结构配对的模具采用软模;R.Truckenmüller等[6]利用下模具注入气体的方法,压印了厚度25 μm、深度125 μm的壳状微沟道聚苯乙烯薄膜,但该方法不适合成型高纵横比的微沟道,且成型后的薄膜厚度均匀性较差。
对于下模具用热塑性材料的选用,硅橡胶更具优势。硅橡胶具有耐高温性能和化学性质稳定等特点,在热压印过程中,即使操作温度超过玻璃化温度,硅橡胶仍能保持较好的稳定性,而且在脱模过程中,硅橡胶的高弹性使其脱模更容易[6]。
本工作采用硅橡胶替代传统下模具,压印成型聚甲基丙烯酸甲酯(PMMA)制品,硅橡胶的本构模型和PMMA的材料模型分别采用Mooney-Rivlin模型和广义Maxwell模型,通过单轴拉伸试验确定不同硬度硅橡胶的材料参数。利用有限元仿真软件ANSYS模拟PMMA制品成型过程,研究压力载荷、压印温度和硅橡胶硬度对PMMA变形的影响。
1 材料的模型和参数
1.1 PMMA
压印材料采用PMMA。PMMA为无定型热塑性高聚物材料,具有密度小、透明度高及热塑性良好等特点[7],在微光学、化学中应用广泛。
PMMA的参数[8]为:弹性模量 3.3 GPa,泊松比 0.39,密度 1.190 Mg·m-3,热膨胀系数6× 10-5m·℃-1,热导率 0.188 4 W·m-1·℃-1,比热容 1 465 J·kg-1·℃-1。
在压印过程中,材料一般在玻璃化温度附近成型,此时材料的性能表现为粘弹性。选用能较好地表述聚合物材料在大变形中的粘弹性的广义Maxwell模型为PMMA的材料模型。该模型的松弛模量E(t)表达式为:

式中,E∞为平衡模量,t为松弛时间,Ei为第i个Maxwell单元的松弛模量,λi为第i个Maxwell单元的时间常数,N为模型中Maxwell单元数量。
通过曲线拟合得到PMMA粘弹性的prony级数[8],如表1所示。

表1 PMMA粘弹性的prony级数
粘弹性具有时温等效性,采用WLF方程表征:
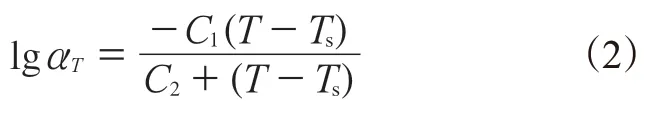
式中,αT为位移因子,Ts为参考温度,C1取14.1,C2取55.82[9]。
1.2 硅橡胶
硅橡胶具有非线性、不可压缩性及大变形等特性,因此为其选择合适的本构模型尤为重要。目前,描述橡胶行为的本构模型主要有Mooney-Rivlin模型和Yeoh模型。Yeoh模型适合模拟炭黑填充天然橡胶的大变形行为,但不能很好地解释双轴拉伸试验结果,且不能描述小变形行为[10]。Mooney-Rivlin模型适合描述中、小变形行为且描述精度高,故选用Mooney-Rivlin模型作为硅橡胶的本构模型。基于应力-应变以唯象理论建立橡胶本构关系,得到硅橡胶应变能密度(W)函数:

式中,I1,I2和I3为Cauchy-Green变形张量不变量,λ1,λ2和λ3为主伸长比,γi为主应变。
应变能密度函数模型为:
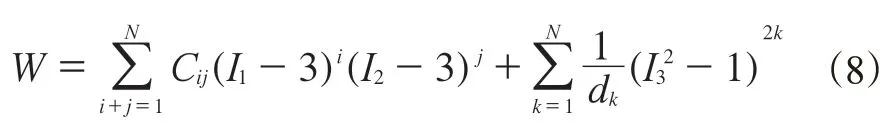
式中,N,Cij和dk为材料常数,当材料不可压缩时,I3=1,j=1。
根据Mooney-Rivlin模型,公式(8)可简化为:

由应变能函数可得到柯西应力张量(σ)的表达式:
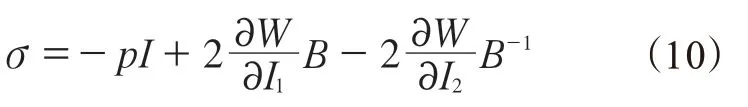
式中,p为不可压缩假设引入的任意流体静压力,B为变形张量,Ii为B的不变张量。
根据单轴拉伸试验原理,公式(10)可简化为:

D.Zhao等[11]研究了不同硬度(邵尔A型硬度为30~60度)橡胶辅助对压印成型的影响,发现硬度大的橡胶成型的微沟道均匀性较好。在此基础上选用邵尔A型硬度为20~70度的硅橡胶进行单轴拉伸试验,结果如图1所示。利用Origin拟合得到Mooney-Rivlin模型中C10和C01的参数值,如表2所示。

表2 硅橡胶单轴拉伸试验拟合参数 MPa

图1 不同硬度硅橡胶的应力-应变曲线
2 有限元仿真模型
根据热压印工艺条件,采用ANSYS软件对热压印仿真模型(见图2)进行分析。为简化模型选用1/4平面应变模型,网格单元类型为Plane 183,PMMA薄膜厚度为0.05 mm,硅橡胶厚度为5 mm。上下模具采用结构钢,模型左侧施加对称边界条件,右侧硅橡胶的横向位移设置为0,下模具与硅橡胶的接触、硅橡胶与PMMA的接触设置为绑定接触,上模具与PMMA的接触设置为摩擦接触,摩擦因数为0.1,下模具固定,上模具施加向下压力。

图2 热压印仿真模型示意
3 仿真结果分析
傅志红等[12]研究了压印时间对PMMA基板流动变形的影响,发现保压时间越长,PMMA填充效果越好,而且温度和压力对PMMA填充效果有较大影响。本试验主要研究压力载荷、硅橡胶硬度、压印温度对PMMA变形的影响。
3.1 压力载荷和硅橡胶硬度对PMMA变形的影响
将压印温度设置为110 ℃,测试不同硬度硅橡胶在500~1 300 N压力下的变形状况,结果如图3所示。从图3可以看出:随着压力增大,微沟道深度增大,当压力增大至一定程度时,微沟道深度达到最大;在同一压力载荷下,硅橡胶硬度越小,微沟道深度越大;当压力为1 300 N时,各硬度硅橡胶均达到模具所设置的最大变形量(200 μm)。

图3 不同硬度硅橡胶在500~1 300 N压力下的变形状况
硅橡胶硬度并不是越小越好,因为硬度越小,横向挤压越大,造成PMMA薄膜厚度不均匀。为研究硅橡胶硬度对PMMA薄膜厚度均匀性的影响,以微沟道中心为原点,分别隔40 μm向两侧取点(共5个点),测定各点的平均厚度,结果如图4所示。通过计算得到不同硬度硅橡胶下PMMA薄膜厚度均匀性方差,结果发现硅橡胶硬度越小,PMMA薄膜厚度均匀性方差越大,但并不是硅橡胶硬度越大,PMMA薄膜厚度均匀越好,相比而言,硅橡胶硬度宜适中。

图4 一定压力下不同位置PMMA薄膜的厚度
3.2 压印温度对PMMA变形的影响
选用邵尔A型硬度为50度的硅橡胶,压印温度分别取90,110,120和130 ℃,测试硅橡胶在400~1 200 N压力下的变形状况,结果如图5所示。从图5可以看出:同一压力载荷下,随着压印温度升高,微沟道深度增大;当压力为1 200 N时,不同压印温度硅橡胶均达到最大变形量;特别是压印温度在120 ℃以上,微沟道深度的变化更显著。
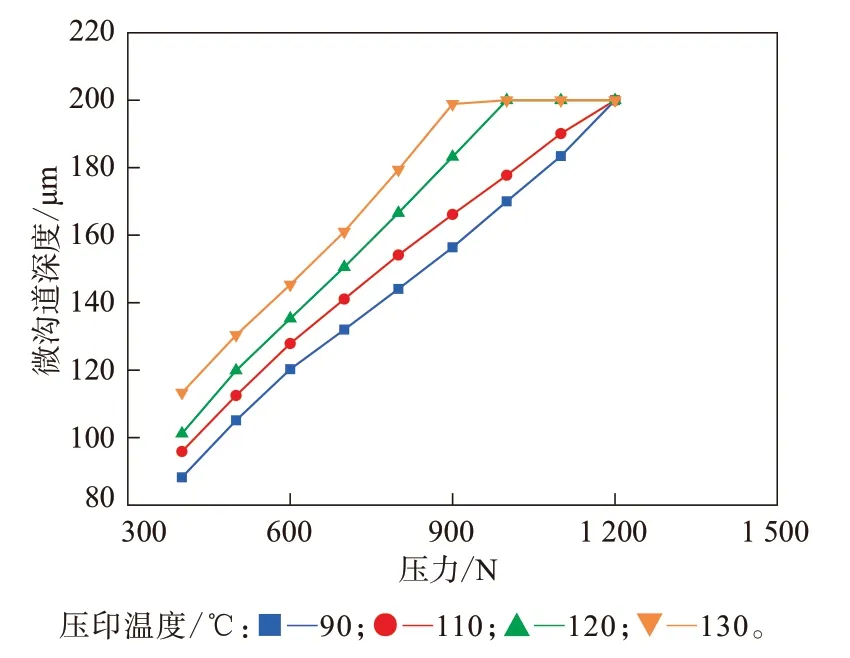
图5 硅橡胶在400~1 200 N压力下的变形状况
以邵尔A型硬度为50度的硅橡胶为例,研究压力载荷为900 N下压印温度对PMMA薄膜厚度均匀性的影响,结果如图6所示。从图6可以看出:在距离微沟道中心80 μm处,PMMA薄膜厚度较小,这是由于在该处PMMA薄膜受到的硅橡胶变形挤压压力较大;随着压印温度升高,PMMA薄膜厚度减小,当压印温度为120 ℃时,薄膜厚度均匀性方差最小。
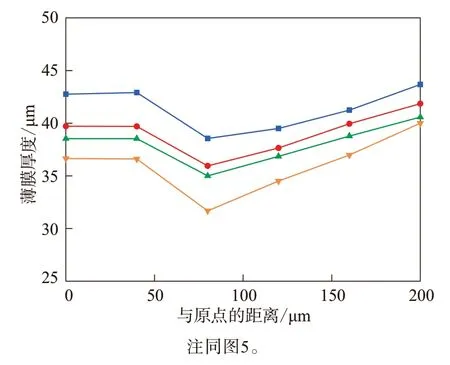
图6 900 N压力下不同位置PMMA薄膜的厚度
4 结论
随着压印温度升高、压力增大,微沟道深度增大;随着硅橡胶硬度增大,微沟道深度减小;当硅橡胶硬度和压力载荷一定、压印温度为120 ℃时,PMMA薄膜厚度均匀性较好;硅橡胶硬度越小,薄膜厚度均匀性越差。
